不同方法求解疏排水引起的地面沉降对比研究

骆 勇，祝晓彬，郭 飞，吴吉春，蒋建国，曾献奎，范亚民，王 栋

(1.表生地球化学教育部重点实验室/南京大学地球科学与工程学院，江苏 南京 210023；2.南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210046；3.江苏省环境科学研究院，江苏 南京 210036)

地下水开发利用和疏排水过程引起的地面沉降问题一直备受关注，抽排水引起的地面沉降问题实际上就是一个渗流场与应力场耦合的问题。水流和地面沉降耦合模型按结合方式分为不耦合的两步计算模型、部分耦合模型和全耦合模型。不耦合的两步计算模型分为完全独立的两步，先计算孔隙水压力，再计算变形，水流及沉降方程中各参数在沉降过程中不随沉降过程发生变化，用于简单计算基坑抽排水引起的沉降计算的土力学经验公式属于此类。全耦合模型基于Biot固结理论，孔隙水压力和变形同时算出，在理论上这种模型最符合沉降物理机制。部分耦合模型介于上述两者之间，孔隙水压力和变形既分步计算，两者之间又相互影响[1]。叶淑君、施小清等[2～4]通过分析长三角地区土层变形特征，采用修正的Merchant模型建立了三维变系数水流和垂向一维沉降组成的部分耦合模型，对长三角区域的地面沉降进行了模拟。熊小峰等[5]基于部分耦合原理，采用TOUGH2和FLAC3D建立抽水引起的三维地面沉降弹塑性模型。在渗流-沉降全耦合研究中，R W Lewis等[6]运用比奥固结理论建立了威尼斯地面沉降模型。金玮泽等[7]以比奥固结理论为基础，建立了地下水疏降与地面沉降变形的水土全耦合模型，可同时求解地下水位和土体变形位移量，并将其与基于Terzaghi有效应力原理地下水渗流与一维垂向固结模型进行对比，取得结果更符合实际。全耦合模型相对部分耦合模型更符合实际情况、更为准确，但是三维全耦合模型物理场控制方程更为复杂、计算量大、需要参数多，所以能进行三维全耦合模型的建立并进行求解的可视化软件很少。近年来，基于偏微分方程设计专业有限元数值分析包的COMSOL Multiphysics被广泛用于多场耦合问题的模拟，只要是一个可以用偏微分方程形式数学模型描述的问题，几乎都可以采用COMSOL Multiphysics求解[8]。结合软件具有的强大后处理功能，使其在机械制造、石油开采等诸多领域应用广泛，但COMSOL Multiphysics应用于求解疏排水引起的地面沉降研究相对较少[9～10]，用于计算地面沉降结果的合理性和可靠性缺乏验证。

基于此，本文基于不同渗透系数条件下的抽水引起地面沉降的理想算例，采用COMSOL Multiphysics进行求解，并同时采用目前较为常用的不耦合的两步计算方法-土力学经验公式、部分耦合的地下水模拟系统软件GMS中SUB模型进行求解，通过结果对比验证COMSOL Multiphysics求解疏排水引起地面沉降的可行性和可靠性。

1 疏排水引起地面沉降计算理论与方法

1.1 土力学经验公式法

土力学经验公式为典型的渗流-地面沉降两步计算模型。第一步计算疏排水引起的水位变化ΔH；第二步根据ΔH求出土层承载压力变化ΔP，进而求出地层压缩量ΔB。计算含水层和弱透水黏性土层的土力学经验公式[11]:

(1)

(2)

(3)

式中:ΔB1——含水层压缩量/m；

ΔB2——黏性土层压缩量/m；

ΔP——水位变化施加于土层的平均荷载/MPa；

M——计算土层厚度/m；

E——含水层弹性模量/MPa；

αv——压缩系数；

e0——孔隙比；

ΔH——水位降深/m；

γw——水的重度/(N·m-3)。

1.2 GMS中SUB模型计算理论

地下水模拟系统软件GMS中SUB模型为渗流-沉降部分耦合模型，水流和沉降模型控制方程：

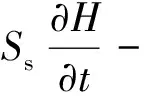
(4)

b1=-ΔHS′skeΔb

(5)

b2=-ΔHS′skvΔb

(6)

式中：Ss——含水层储水率/m-1；

K——渗透系数/(m·d-1)；

H——水头/m；

Qm——源汇项/d-1；

b1——土体的弹性变形量/m；

b2——土体的非弹性变形量/m；

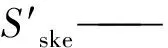
Δb——压缩土层的厚度/m；

ΔH——水头变化值/m。

两场控制方程通过水头项进行耦合。数值计算中，先求解水流控制方程，然后将计算得到的水头变化代入沉降控制方程计算土层变形。上述水流模型与沉降模型的耦合方式属于分步耦合[12]，也可称为部分耦合。

SUB模块可以用垂向一维扩散方程模拟较厚弱透水夹层随时间变化的滞后排水过程：

(7)

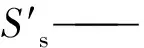
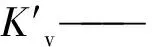
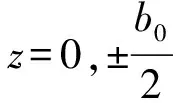
(8)

由式(8)计算的夹层释水时间参数远超过模拟时间步长时，就必须考虑夹层的滞后释水。

1.3 COMSOL Multiphysics模型计算理论

COMSOL Multiphysics采用渗流-沉降完全耦合模型，考虑渗流场变化对沉降影响，而沉降的变化又会影响渗流场，两者之间相互耦合、相互影响。渗流场控制方程：

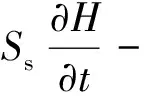
(9)

(10)

式中：K——渗透系数/(m·d-1)；

ux,uy,uz——x、y、z方向上的位移分量；

α——比奥固结系数；

γw——水的重度/(N·m-3)；

Ss——储水率/m-1；

H——水头/m；

εv——体应变。

应力场控制方程：

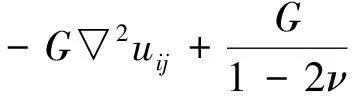
G=E/[2(1+ν)]

(11)

式中：uij——位移变量；

G——土体的剪切模量/MPa；

v——土体的泊松比；

E——杨氏模量/MPa；

ρf——水的密度/(kg·m-3)；

Hij——水头/m。

(12)

Ss=nχf+(1-n)χp

(13)

式中：n0——初始孔隙度；

K0——初始渗透系数/(m·d-1)；

χf——多孔介质骨架压缩系数；

χp——孔隙压缩系数。

2 疏排水引起地面沉降算例模型

算例模型为一单井抽水引起地面沉降模型。含水系统为二层结构，表层为弱透水的黏土层(层厚20 m)，下层为含水砂层(层厚30 m)，水平范围是以抽水井为中心的500 m×500 m区域。含水系统结构见图1。

初始条件：设定算例研究区初始水位标高为45 m。

边界条件：设置研究区上、下边界为零通量边界，研究区四周边界为给定水头(45 m)边界。

基本参数：含水砂层水平渗透系数取Kx、Ky设为4 m/d、垂向渗透系数Kz取0.4 m/d，黏土层Kx、Ky取0.004 m/d、Kz取0.000 4 m/d；含水层孔隙度n0取0.3，黏土层孔隙度n0取0.6。

模拟情景：基于模型，考虑单井抽水的情形(抽水量为1 000 m3/d)，设置两个时间应力期，抽水应力期时长50 d(第0～50天)，停抽恢复应力期时长200 d(第51～250天)。

计算结果：对含水系统的水位变化及引起的沉降量进行计算。

图1 理想算例含水系统结构Fig.1 A schematic diagram of the structure of an ideal example water-bearing system

3 不同计算方法求解疏排水引起的地面沉降

使用土力学经验公式法、GMS中SUB模型以及COMSOL Multiphysics分别计算上述单井抽水模拟情景下引起的地面沉降。

3.1 经验公式法求解

采用经验公式计算单井抽水引起不同水位变幅时的地面沉降值。降水面以下的土层通常不产生明显固结压缩量，抽水产生的地面沉降主要由最终降水面至原始地下水面之间土层变形产生[11]。本文算例模型中黏土层厚20 m，下层承压含水层厚30 m，初始水位45 m，当水位降低幅度在15 m以内时只计算黏土层压缩量。采用经验公式计算不同水位变幅下的土层沉降量涉及有关参数取值见表1，水位下降引起的地面沉降量计算结果见图2，沉降和水位下降同步发生，沉降量随水位降深增大而逐渐增大。

图2 经验公式计算不同水位变幅下的土层沉降量Fig.2 Analytical solution under different water levels under the soil settlement

土层孔隙比e0压缩系数α0/kPa-1计算土层厚度M/m粘土层1.50.1与水位变动幅度一致

3.2 GMS中SUB模型求解

采用GMS中SUB模型求解算例模型抽水引起地面沉降的有关参数取值[16～17]见表2。在模型中，承压含水层未分配滞后夹层，将弱透水层进行多层划分。计算得到距抽水井不同距离处含水层水位变化与地面沉降量变化对比见图3。距抽水井不同距离处(10 m、25 m、50 m)，地面沉降量随水位变化规律基本一致，水位下降导致沉降发生，水位降深越大、沉降越明显，水位回升导致地面沉降逐步恢复，水位回升至初始状态时，沉降并未完全恢复，存在一个不可恢复的永久沉降量。在0～50 d时抽水井抽水，各处水位都在下降，各处沉降量随着水位的下降而逐渐增大。距抽水井越近水位下降幅度越大，沉降量越大。距抽水井越远水位下降幅度越小，沉降量越小。51～250 d时抽水井停止抽水，距抽水井不同距离处水位立即同时回升，在第120 d左右水位恢复到初始水位。根据前人相关研究[17～19]，SUB沉降模型可以模拟疏水时弱透水夹层的沉降滞后效应，但在本文模型设置情景下，沉降滞后现象不明显。

图3 GMS SUB模型计算下距抽水井不同距离处水位及沉降量变化对比图Fig.3 Change in the water level and settlement at different distances from the pumping well calculated with the GMS SUB module

土层弹性骨架储水率S′ske/m-1非弹性骨架储水率S′skv/m-1弹性骨架储水系数非弹性骨架储水系数垂向渗透系数K′v/(m·d-1)含水砂层——3.4×10-43.4×10-2—粘土层4.0×10-54.2×10-3——4.0×10-6

3.3 COMSOL Multiphysics求解

采用COMSOL Multiphysics求解算例模型抽水引起地面沉降的有关参数取值[20]见表3，含水层中距抽水井不同距离处(10 m、25 m、50 m)水位变化与沉降量变化对比见图4，不同距离处水位和沉降量总体变化规律一致。在0～50 d时抽水井抽水，各处水位都在下降，各处沉降量随着水位的下降逐渐增大。距抽水井越近水位下降幅度越大，产生的沉降量越大；距抽水井越远水位下降幅度越小，沉降量越小。51～150 d时抽水井停止抽水，距抽水井不同距离处(10 m、25 m、50 m)水位立即产生较大回升然后逐渐恢复到初始状态，但距抽水井不同距离处(10 m、25 m、50 m)沉降量变化出现滞后现象。距抽水井越远处，沉降滞后时间越长，距抽水井10 m处发生沉降的趋势在第60 d开始停止，随着水位的恢复地面发生回弹，沉降量逐渐变小，在模拟期结束后仍有约0.63 mm的沉降量。距抽水井25 m处发生沉降的趋势在第64 d开始停止，随着水位的恢复地面发生回弹，在模拟期结束后仍有一个0.5 mm左右的沉降量。距抽水井50 m处发生沉降的趋势在第70 d开始停止，随着水位的恢复地面发生回弹，沉降量逐渐变小，在模拟期结束后仍有约0.24 mm的沉降量。距离抽水井越远，产生的最大沉降量越小、模拟期结束时的沉降量越小，但滞后于水位变化的时间却越长。

图4 COMSOL Multiphysics计算下距抽水井不同距离处水位及沉降量变化对比图Fig.4 Comparison of water level and settlement variation at different distances from the pumping well calculated with the COMSOL Multiphysics

土层泊松比ν0密度ρ/(kg·m-3)杨氏模量E/MPa储水率S/m-1含水层0.4892 150400.008黏土层0.4982 000500.000 04

4 地面沉降计算结果分析与讨论

4.1 计算结果对比分析

4.1.1COMSOL Multiphysics与经验公式法计算结果对比

计算应力期内，由COMSOL Multiphysics计算得到距抽水井10 m、25 m、50 m处最大水位变幅分别为4.3 m、3.1 m、2.2 m。在相同水位变幅条件下，用经验公式和COMSOL Multiphysics计算出距抽水井不同距离处对应最大沉降量对比见表4。不同水位变幅下，COMSOL Multiphysics与经验公式最大沉降量计算值虽有偏差但较为接近，说明本文建立的COMSOL Multiphysics模型可靠。

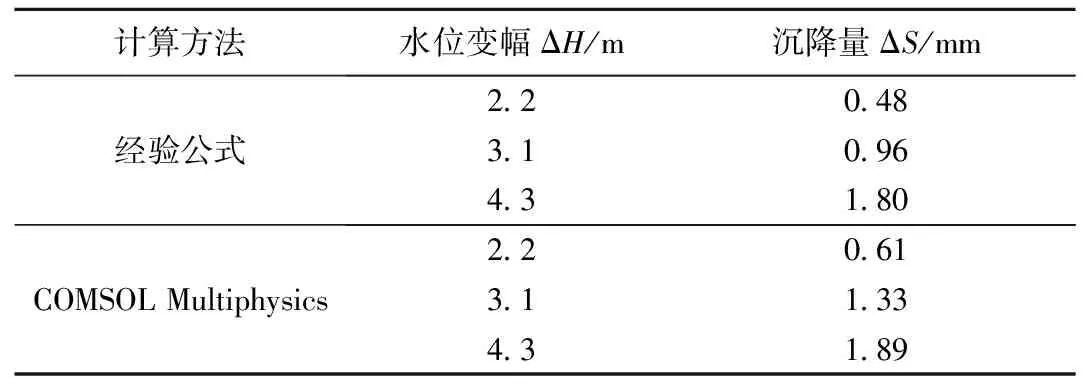
表4 相同水位变幅下经验公式与COMSOL Multiphysics沉降量计算结果对比Table 4 Comparison of the settlement calculation results under the same water level variation calculated with the empirical formula and COMSOL Multiphysics

4.1.2COMSOL Multiphysics与GMS中SUB计算结果对比

距抽水井25 m处GMS的SUB模型与COMSOL Multiphysics水位变化、沉降量变化计算值对比见图5，结果表明2种方法计算沉降量值总体接近。在本文模型设置情景下，GMS中SUB模型计算结果的水位与沉降几乎同步变化，沉降变化滞后现象不明显；而COMSOL Multiphysics中沉降滞后现象相比前者较为明显，且图4表明距抽水井越远沉降滞后越明显。在抽水初期，不同模型计算水位呈现大致相同幅度的降低，但GMS中SUB模型相比COMSOL Multiphysics沉降量增大速率和幅度明显，表明GMS中SUB模型沉降量对水位变化响应快。沉降回弹时，COMSOL Multiphysics计算的沉降量回弹过程较为缓慢，而GMS中SUB模型计算的沉降在抽水停止后瞬间产生一个较大幅度的回弹。对比实际沉降对水位变化的响应规律，COMSOL Multiphysics计算结果更符合实际沉降特征。这是因为GMS中SUB模型是渗流-沉降部分耦合模型，通过先计算地下水渗流方程，求出水头变化后，即由孔隙水压力变化计算地面沉降，未将孔隙水压力变化与沉降同时考虑。COMSOL Multiphysics中充分考虑了渗流-沉降场的耦合，不仅考虑了孔隙度、渗透率等土体参数的动态变化，还考虑了土体的黏弹性、黏塑性，抽水引起渗流场改变，渗流场改变使得孔隙水压力发生变化，土体将产生沉降，而土体的沉降又会改变土体的孔隙度、渗透率从而影响渗流场，上述过程即实现了流固全耦合。

图5 距抽水井25 m处GMS SUB模块及COMSOL Multiphysics计算下水位及沉降量变化对比图Fig.5 Comparison of water level and settlement change at the distance of well 25 m from the pumping well calculated with the GMS SUB module and COMSOL Multiphysics

4.2 渗透系数K对地面沉降量计算结果的影响讨论

为进一步研究不同模型计算疏排水引起地面沉降的差异，考虑不同渗透系数对地面沉降计算结果的影响。因为渗透系数对流场影响较大，而流场中水头的变化是导致沉降的直接因素，因此渗透系数大小对沉降量影响同样较大。采用不同方法计算不同渗透系数条件下抽水引起的地面沉降，可以进一步对方法的有效性进行比较。GMS中SUB模型的渗透系数K为一定值，虽然也有学者对SUB模块这一不足进行了研究，如施小清等[21]针对黏性土压缩过程中各土体参数都发生变化的问题，对MODFLOW-2000中的SUB模块进行了修正，较好刻画了地面沉降过程中黏性土释水的特点。但相比COMSOL Multiphysics从机理上实现完全的流固耦合，无疑COMSOL Multiphysics具有更好应用条件。

对不同初始渗透系数条件下，距抽水井25 m处，GMS中SUB模型和COMSOL Multiphysics求解的沉降结果进行比较。渗透系数逐渐增大(Kx、Ky由4 m/d增大到10 m/d，再增大到30 m/d；Kz由0.4 m/d增大到1 m/d，再增大到3 m/d)，地面沉降量计算结果见图6。结果表明，算例条件下，两种方法计算结果均反应出渗透系数越大沉降量越小的现象，渗透系数越大，相同抽水条件下水位变化越小，和实际含水系统中对应的水位和沉降特征吻合。COMSOL Multiphysics计算的沉降量滞后时间随着渗透系数的变大而减小，GMS中 SUB模型计算的沉降量在本文模拟情景下滞后效应不明显，在抽水停止时会发生较大回弹，并且随着渗透系数的变大趋于稳定的时间变快；在抽水初期，GMS中SUB模型沉降量计算值增幅较COMSOL Multiphysics更大。两种方法计算结果的差异性是由方法理论控制方程的差异导致的：完全耦合模型以比奥固结理论为基础，对土体变形与孔隙水压力同时进行求解，将沉降模型与水流模型统一于同一物理空间，并且不作固结过程中总应力为常量的假设；部分耦合模型考虑了土体仅垂向上发生变形的情况，假设总应力不随时间变化，且渗透系数等土体参数不变。完全耦合的COMSOL Multiphysics模型计算结果更为合理。渗透系数越小、沉降越易发生的地层，COMSOL Multiphysics模型计算的沉降过程滞后越明显，水位回升后沉降越难以恢复，结果比GMS中SUB模型计算结果越合理。

图6 不同渗透系数下距抽水井25 m处GMS SUB模块与COMSOL Multiphysics沉降量计算值对比图Fig.6 Comparison of settlement at the distance of 25 m from the pumping well at different coefficients of permeability with the GMS SUB module and COMSOL Multiphysics

5 结论

分析比较不同方法计算抽水引起的沉降量计算结果和反应的沉降过程，得到如下结论：

(1)COMSOL Multiphysics与经验公式、GMS中SUB模型计算算例条件下的沉降量计算结果总体较为接近，表明COMSOL Multiphysics求解疏排水引起的地面沉降可行。

(2)在本文模拟情景下，COMSOL Multiphysics计算的沉降量出现明显滞后于水位变化的规律，且距抽水井越远沉降滞后时间越长；而在相同模拟情景下GMS SUB模块沉降滞后现象不明显。基于渗流-应力场全耦合的COMSOL Multiphysics模型计算结果更合理。

(3)与GMS中SUB模型计算结果相比，渗透系数越小，COMSOL Multiphysics模型计算结果更能反应实际沉降过程特征。