OpenMP在CO2地质储存数值模拟并行计算中的应用

杨艳林， 许天福， 靖 晶

(1.武汉地质调查中心，湖北 武汉 430205；2.吉林大学环境与资源学院，吉林 长春 130021；3.中国地质大学(武汉)环境学院, 湖北 武汉 430074)

CO2地质封存作为CO2减排的重要方式，受到世界各国政府与大量学者的广泛关注。数值模型在CO2地质封存场地选择、封存能力与安全性评估等方面发挥了重要作用[1～6]。TOUGH2-ECO2N程序是专门用于CO2地质储存的数值模拟器，模拟结果准确可靠，得到了广泛应用[7～9]；但随着研究的不断深入，其对场地级精细模拟和长时间跨度的高仿真数值模拟提出了迫切需求。基于此，国内外学者提出了OpenMP、PVM、MPI和GPU等并行计算技术[10]，同时开发出一些通用的并行求解器，如AZTEC、PETSc、Hypre[11]；以及区域分解工具，如Metis、ParMETIS。在CO2地质封存领域也取得了一些成果，如国外PFLOTRAN、AM、HBGC123D以及PARSWMS等并行模拟器，成功应用于CO2地质封存；以及国内张可霓等[12]基于MPI开发了TOUGH2-MP，可快速地完成CO2地质封存数值模拟；朱彤[13]利用GPU，米东等[14]利用MPI加速TOUGHREACT，完成了注入CO2的水岩相互作用模拟。这些研究在加快计算速度和提高求解规模方面取得了一定的进展，同时也为本文的研究提供了参考。

OpenMP是共享编程的典型编程模型，是计算机硬件、软件厂商联合发表的共享内存编程应用程序接口，具有编程简单、灵活、开发周期短、并行效率高、支持多种语言和多种操作系统等特点。本文在Windows PC机上，提出了利用OpenMP并行化TOUGH2-ECO2N模拟器的方法，大大增强了其计算规模及效率的能力。

1 TOUGH2-ECO2N数值模拟器简介

1.1 数学模型

深部岩土体介质中地下流体的控制方程是依据质量和能量守恒准则建立的，如下：

(1)

其中，Aκ可分为质量项与能量项，质量项主要包括水、盐和CO2等，即式(2)；能量项是固相、液相与气相中的能量和，即式(3)。同样Fκ也分为质量流量与能量流量，质量流量主要采用达西定律来描述，即式(4)；能量流量采用热传导定律来刻画，即式(5)。式中各参数意义见表1。

(2)

(3)

(4)

(5)

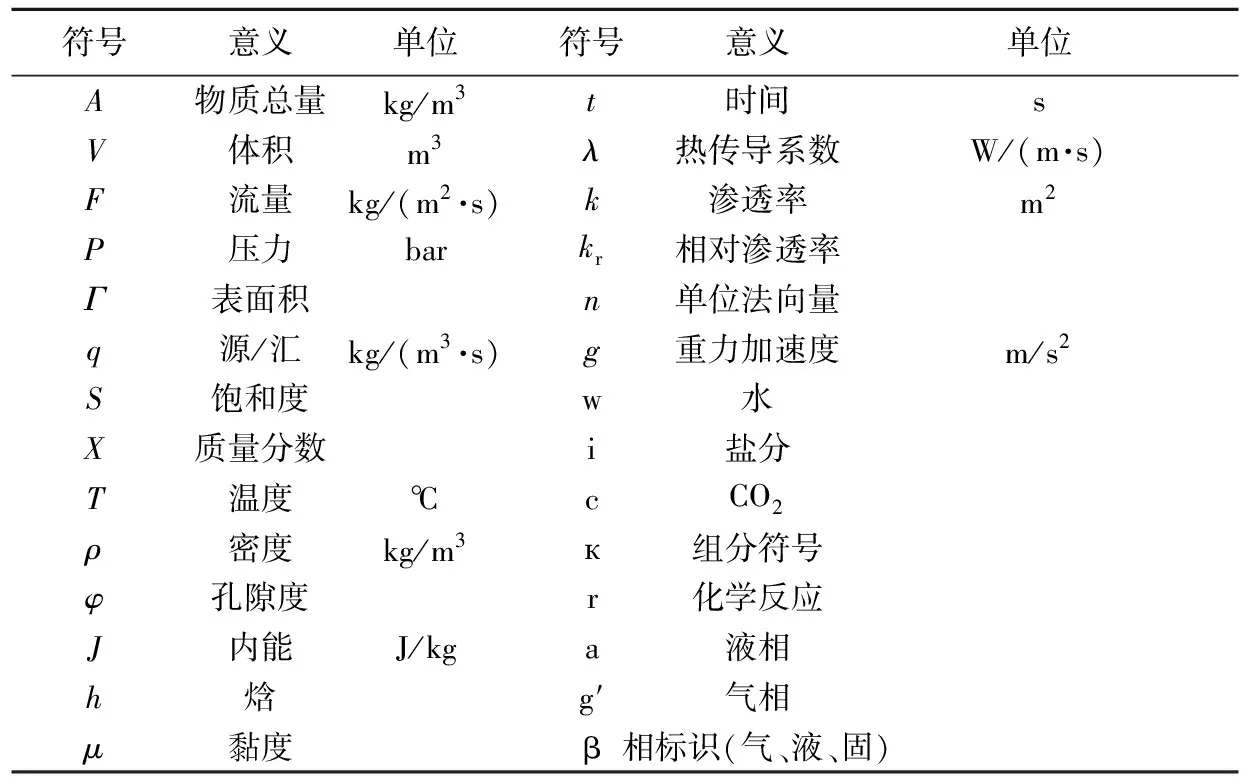
表1 模型中所涉及的符号及意义Table 1 Symbols and meaning in these models

1.2 模拟器程序结构

TOUGH2是一个面向过程的程序，主体采用FORTRAN77语言编写，包括一个主程序和若干个状态方程模块(图1中的EOS，用于计算单元的次级主要变量)，不同状态方程模块，对应不同功能的模拟器，如对于CO2地质封存则采用其中的ECO2N模块。通过对TOUGH2源程序分析，其程序流程见图1。

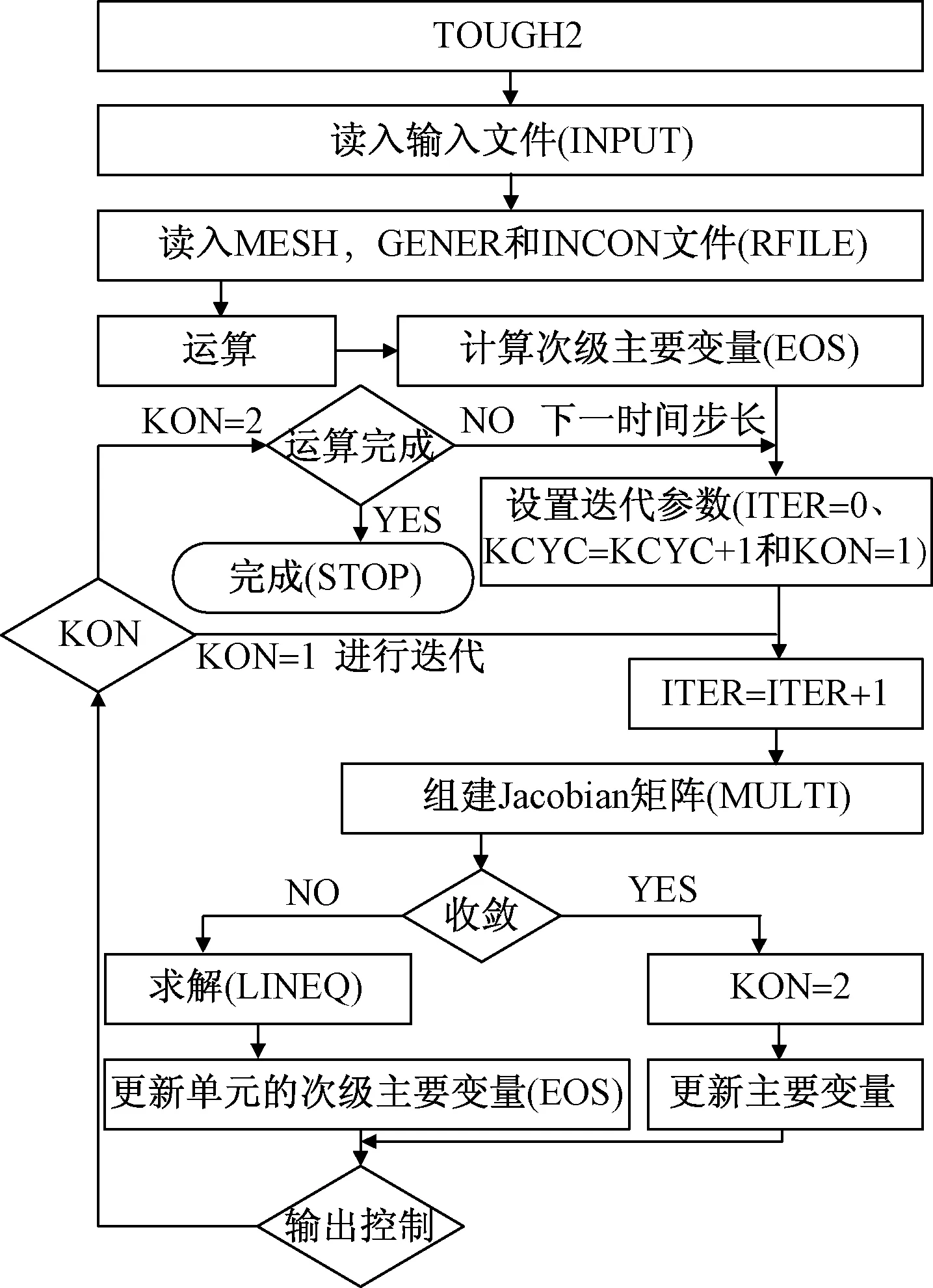
图1 TOUGH2模拟器程序简化流程图Fig.1 Simplified flow chart of the TOUGH2 simulator

1.3 空间时间离散及矩阵存储结构

TOUGH2模拟器是采用积分有限差进行空间离散、时间向前差分进行时间离散，并通过程序中的“MULTI”来组建大规模矩阵方程(又称Jacobian矩阵)。矩阵方程具有非对称、强非线性和高稀疏的特点；最后采用三元数组的方式进行存储，生成后的矩阵形式见图2。

图2 Jacobian矩阵存储(30个单元等温模型)Fig.2 Jacobian matrix storage (Isothermal models of 30 cells)

1.4 模拟器耗时评估

为了了解程序运行时的耗时部分，本文以中大规模的模型(2 500，10 000，40 000)为算例进行分析。结合前面对TOUGH2源程序结构的分析，可将模拟器分为四大过程：首先是对各种输入文件进行读入；第二步是计算每个单元的状态(EOS模块)；第三步是组建矩阵方程(MULTI模块)；最后是对矩阵方程进行求解。第一部分耗时较小，第二、三和四部分是模拟器的主要耗时部分，其中方程求解所占的时间比例最大，达到70%以上，而且随着模型规模的增大，这个比例还会增大(图3)。

图3 主要模块执行时间对比(20 a)Fig.3 Comparison of the module execution time (20 years)

单元的状态更新与组建Jacobian矩阵所耗的时间相当，因此在方程求解模块进行并行时需引起高度的重视。方程的求解方法，通常有直接法和迭代法，但由于直接法需要更多的计算机时和存储空间，而迭代法弥补了其不足，尤其是处理大规模的矩阵时，优势更加明显，故只考虑迭代法的并行化。通过对迭代法的分析(以稳定双共轭梯度迭代法-DLUSTB为例)，其主要包括三个功能区：格式转换、预处理(LDU分解)和迭代求解等。为了进一步了解其在求解模块中的执行时间，在上述方案中，也将对应的执行时间进行了深入分析。格式转换和迭代求解是主要的耗时部分，而且随着模型规模的增大，迭代求解的执行时间会更长(图4)。

图4 求解模块中不同功能区的执行时间Fig.4 Execution time of different functional areas in the solving module

综上分析，EOS模块、MULTI模块、格式转换和迭代求解是算法改进和并行化的重点。

2 并行算法的实现

2.1 OpenMP简介

OpenMP是一个为共享存储的多处理机上编写并行程序而设计的编程接口，其功能的实现得到两种形式的支持：编译指导语句和运行时库函数，并且可灵活地控制程序运行。OpenMP使用的是Fork-Join(交叉-合并)并行执行模型。当程序运行到并行区域时，会创建新线程或者唤醒已有线程(Fork过程)，此时主线程和派生线程共同工作；当执行完并行区域，派生线程会退出或挂起，回到主线程(Join过程)。OpenMP具有与标准Fortran、C和C++等语言无缝集成，只要在程序中加入OpenMP编译命令，即可完成并行；通过一些常见函数设置、获取并行环境参数，如omp_set_num_threads函数来设置程序的线程数、omp_get_thread_num获取当前线程号等。

2.2 并行算法的实现

基于TOUGH2模拟器算法以及OpenMP并行化的特点，按以下几方面进行了改进并实现了并行。

(1)动态内存分配

TOUGH2源程序数组采用静态内存分配，导致部分数组拥有大量空间而浪费，而部分数组则不够，带来十分不合理的内存使用方式，同时对于大规模计算问题，常常无法编译成功。基于此，采用面向对象的思想和动态内存分配的方式重组了源程序。

(2)并行化方案

通过前面对模拟器中的耗时分析，程序的计算时间主要分布在EOS模块、MULTI模块和方程求解等部分。故在进行并行化时，主要针对这些区域进行并行化，而且对OpenMP程序本身运行的线程锁、同步开销和负载不均衡等关键问题也进行了优化。

(3)跳转语句

由于OpenMP并行的限制，循环语句中应该是单入口与单出口，不易使用跳转语句，故需对程序中的跳转语句进行处理。其中一部分采用原子锁来处理，另一部分则需对程序进行重构。

(4)参数优化

源程序中各函数中的变量以及中间变量非常多，若在并行时都采用私有变量来处理(private、privatefirst、lastprivate或threadprivate)，则会带来大量的开销，对并行的优化效果非常不利。鉴于此，对程序采取两种处理方式：第一是将具有多个功能块的函数，分解为多个独立的子函数，一方面可以减小局部的参数传递，另一方面程序的可读性也得到了增强。第二是对多余的参数进行剔除或替换，重要的参数在函数之间采用参数传递。

(5)相关性的处理

一般来说，若两个计算块之间具有某种相关性，则它们无法或很难进行并行化，如在组建Jacobian矩阵计算单元之间质量与能量项、进行的不完全LDU分解、以及稀疏矩阵进行乘等部分。这时可借助临时数组来记录中间数据，后再进行统一处理。

(6)并行化原则

在进行OpenMP并行化时，主要遵从三个原则：第一，减小功能之间或数据之间的依赖性，尽可能有更大的并行区域，减少并行区域与串行过程的相互交叉；第二，采取更大功能范围内的并行，减小局部功能的并行，以减少并行线程申请的时间开销；第三，缩减并行区域的私有变量个数、原子锁、时间同步等耗时操作，并考虑负载不均衡等问题；第四，尽量保持原来程序的风格。

3 并行实验结果分析

3.1 模型设计及介绍

模型是以鄂尔多斯CCS示范场地的石千峰组地层为研究对象，模型的水平范围是以注入井为中心的5 km，厚度为291 m(图5)。在进行并行模拟器测试时，主要考虑以下两个方面：第一是改进后的模拟器与原有模拟器的正确性与效率比较；第二是并行化模拟器的并行化效率。针对第二方面，设计了三个模型，分别代表小、中与中大规模，来探讨模拟器的并行加速情况，具体模型方案设计见表2。

图5 模型测试网格Fig.5 Model test grid

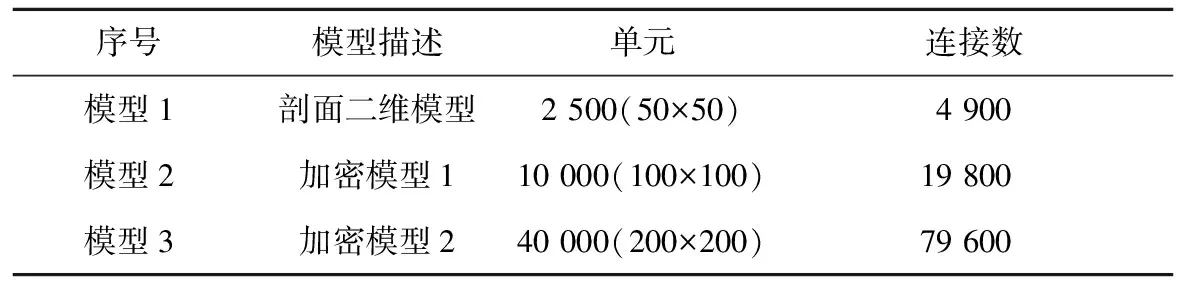
序号模型描述单元连接数模型1剖面二维模型2 500(50×50)4 900模型2加密模型110 000(100×100)19 800模型3加密模型240 000(200×200)79 600

3.2 实验平台

本次实验在PC机上完成，CPU为Intel(R) Core(TM) i7-2600 CPU@3.4 GHz，内存8 GB，操作系统为32位Windows 7，编译器采用Microsoft开发的支持OpenMP2.0的Visual Studio 2005。

3.3 模拟器结果对比

在程序编译时取消OpenMP支持，则改进后的模拟器即为单机版。下面针对方案1，分别运用改进前后的模拟器进行运算，并进行结果对比分析。图6是改进前后模拟器运算的CO2不同封存形式历时曲线。可知改进前后模拟器的运算结果稳合较好。而且改进前后模拟器的运算结果数值是一样的(只存在结果输出的舍入误差，表3)。故不难得出，改进后的模拟器是可靠的、正确的。

图6 CO2封存量历时曲线对比(气、液、总)Fig.6 Duration curves comparison of CO2storage capacity (in gas, liquid, and total)

图7是改进前后两种模拟器的运算总时间对比；由图上的蓝线可知，改进后模拟器的运算时间比原模拟器少，最大可达到1.28倍的加速，最小可达到1.12倍的加速。

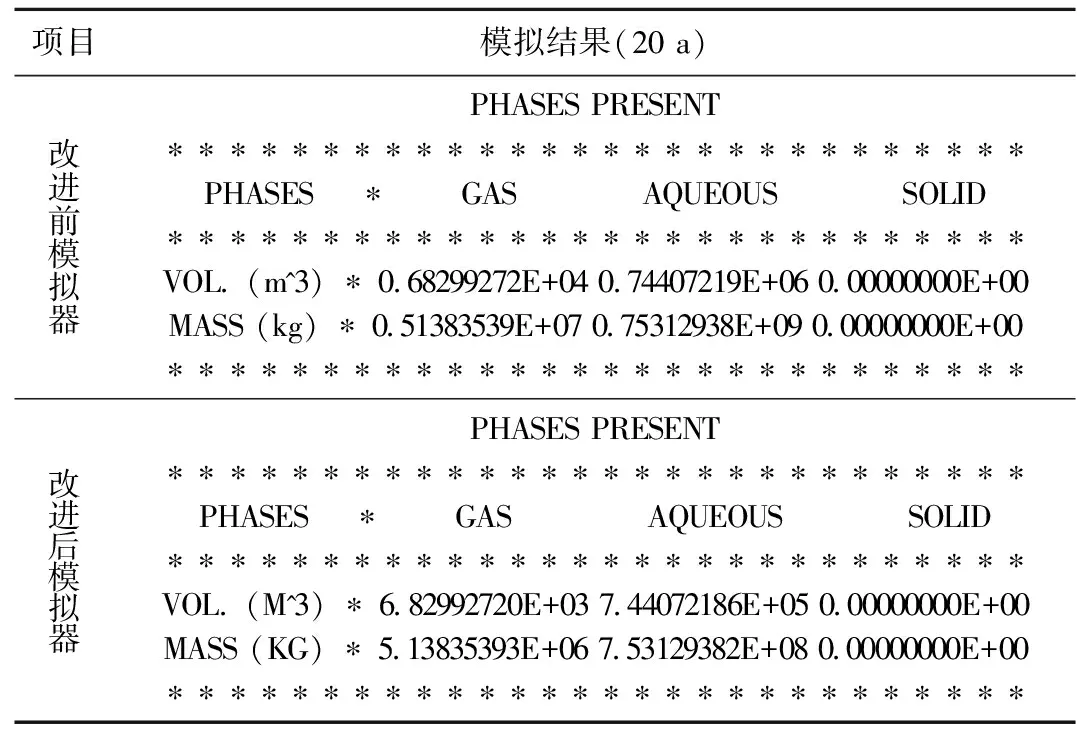
表3 模拟器改进前后模拟结果对比Table 3 Comparison of simulation results before and after the improvement simulator

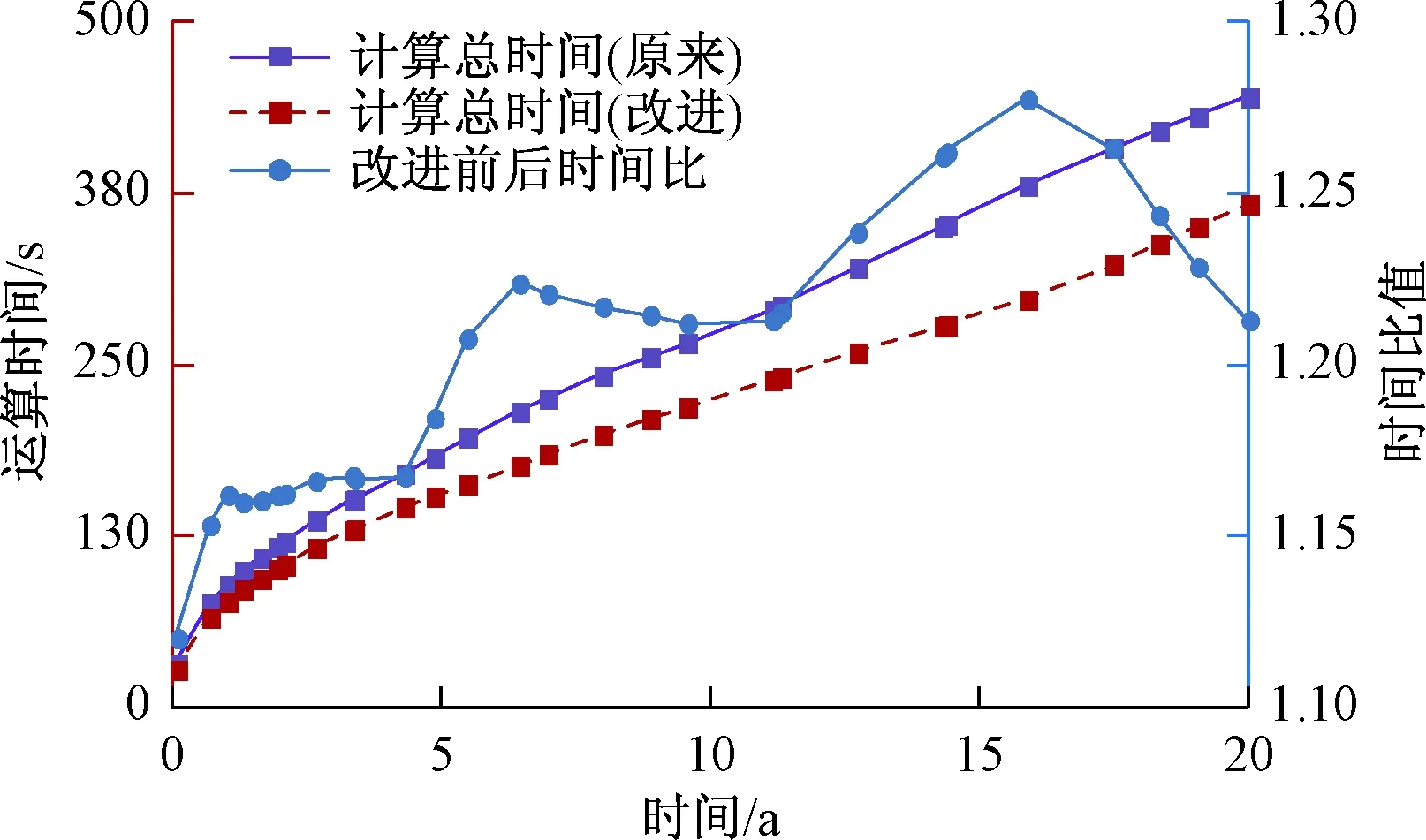
图7 新旧模拟器运算时间对比(模型1)Fig.7 Comparison of computing time between the new and old simulator in the first model

由以上对比不难得出，改进后模拟器的运算结果是可靠的，而且运算效率比原来高。

3.4 并行模拟器模拟结果对比

常用的浮点计算机都提供符合IEEE-754标准的单精度和双精度运算，常见的计算机系统都能够支持4倍精度运算，故在进行浮点运算时都会存在一定的舍入误差。鉴于此，本文对不同核数的模拟器也进行了对比研究，以了解在当前并行框架下，并行模拟器的误差大小和稳定性。

图8是不同核数对模型1运算的CO2封存量与单机运算CO2封存量之差历时曲线；对比分析有：2核的运算结果与单核的运算结果相差为零；4核与单核的相差最大，最后基本稳定在20 kg，这个误差相对于CO2的总封存量(20 a时，1.84491683E+07 kg)非常小，误差仅0.000108%。故在当前的并行框架下，并行模拟器的运算结果是可靠的、稳定的。

图8 不同核之间CO2封存总量之差Fig.8 The difference between the total amount of CO2 sequestration in different CPU numbers

3.5 加速效率对比

加速比(Sp)和执行效率(E)是测试并行算法加速效果的2个重要指标。由表4对比分析可知：并行化处理可明显加快模拟器的运算速度，即加速比会随着核数的增加而增大，原因在于将计算任务分解到多个处理器上，减少了单个处理器的计算量，因而可显著地减小计算时间。在当前模型中，4核可以达到2.28倍的加速比。但随着线程数的增加，模型的执行效率呈现减小的趋势；这主要是由于随着线程数的增多、线程的创建与销毁，以及各个线程之间的负载不能达到完全的负载平衡，由此带来了时间延迟而拖慢了执行效率。同时由于模拟器中还存在许多串行部分，并行效率还有待进一步提高，以达到理想的并行效率。

为了进一步了解各个并行块的执行情况，本文也将其执行时间进行了对比分析。图9是模型2中主要并行块的执行时间历时曲线。EOS模块和MULTI模块都可得到明显的加速；方程求解的加速稍小。通过对方程求解中不同功能块进行对比，格式转换的并行加速效果较明显，预处理和迭代求解的加速效果稍小。

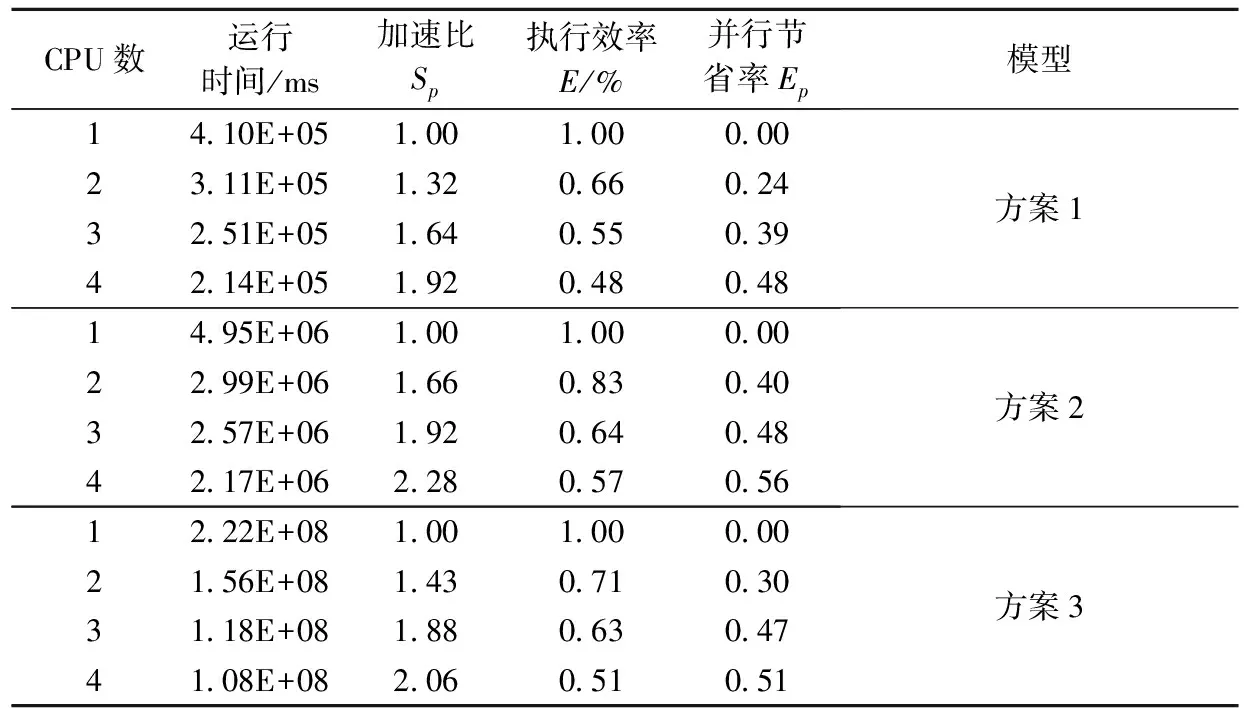
表4 不同处理核数下并行处理加速情况Table 4 The parallel processing acceleration in different CPU numbers

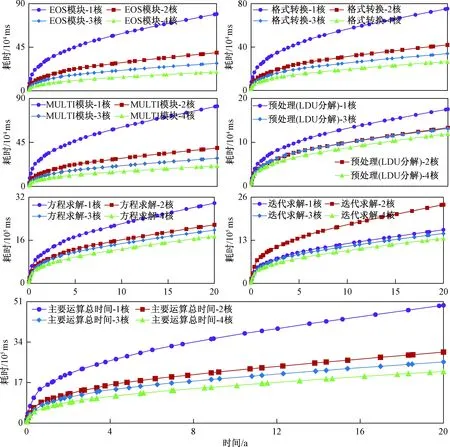
图9 模型2中不同核的执行时间对比Fig.9 Execution time comparison of different CPU numbers in the second model

4 结论

(1)通过分析改进前后的模型器计算结果：改进后模拟器的算法是正确可靠的，且改进后模拟器的执行效率得到了提高，在2 500个单元的模型中，执行速度提高1.12～1.28倍。

(2)由并行模拟器模拟结果对比分析，不同核之间由于计算机的浮点运算误差而引入的数值离散是非常小的，故在OpeMP框架下研发的并行模拟器是可靠的、稳定的。分析方案2的运算执行情况，在4核时，可以达到2.28倍的加速。

(3)由于改进后的模拟器还存在一些串行执行部分，以致未能达到理想的并行效率；同时与已有的并行模拟器进行对比研究，将是以后的研究方向。