典型考题研究：同类收集与成果扩大——从2018年福建中考卷第25题说起

☉江苏省如皋市经济技术开发区袁桥初级中学 陆海燕

中考复习期间学生会涉及大量习题，这些习题的来源主要是全国各地历年来的中考试题，而有些训练的效果好些，有些训练的效果却不甚如意.究其原因，当然与学生的思维水平、运算能力、记忆能力有关，但教学法上的研讨与改进也是一个值得深入思考的话题.比如抛物线有很多奇异的性质（如准线、焦点的性质，由于多地中考试题曾出现过，大家现在已比较熟悉），初中教材上涉及不多，但通过练习不少中考试题，优秀学生也能一眼洞察、看清问题结构，然而也有些偶尔出现一次的奇异性质，因为满足于一题一解或一题一答，缺少对问题结构的反思与揭示，使得优秀学生也不能深刻认识和理解一类问题结构，这是值得我们在解题教学中加以改进的.本文从2018年福建省中考卷第25题的思路解析说起，关联同类、逆向拓展，并提出一些教学建议，供研讨.

一、考题与思路突破

考题1：（2018年福建卷，第25题）已知抛物线y=ax2+bx+c过点A（0，2） .

①求抛物线的解析式；

②点P与点O关于点A对称，且O、M、N三点共线，求证：PA平分∠MPN.

思路突破：

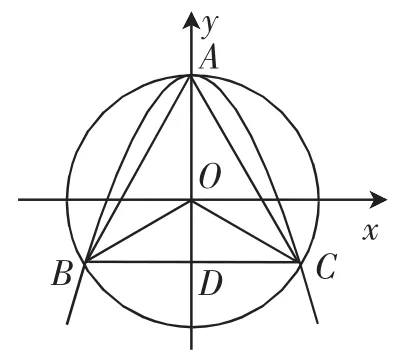
图1

（2）①分别解读：条件“x1＜可得在y轴左侧y随x的增大而增大；条件＜0”可得在y轴右侧y随x的增大而减小.于是可确认该抛物线的对称轴为y轴，且开口向下.可设抛物线的解析式为y=ax2+2.接下来只要画出草图辅助分析，如图1.

结合等边三角形ABC与圆O的半径为2，可得出点B、点C的坐标分别为选择其一代入y=ax2+2，可得a=-1，于是抛物线的解析式为y=-x2+2.

②解法1：构造如图2所示的草图分析.

设点M（x1，-+2）、N（x2，-+2）.由于直线MN经过原点，可设MN：y=kx.

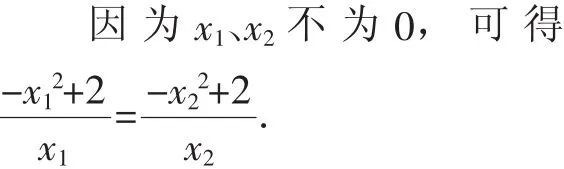
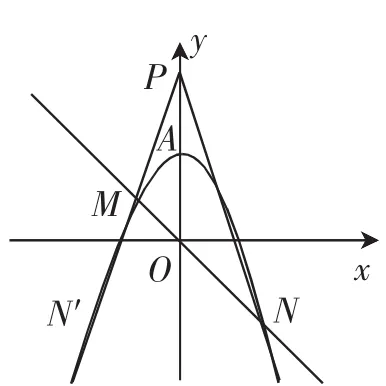
图2

由P是点O关于点A的对称点，易得OP=4，即点P（0，4），可设PM：y=k2x+4.把M点的坐标代入，可得

解法2：为了便于对比，我们再构造图3所示的草图变式（点M、N的位置发生了变化）分析.

先设直线MN的解析式为y=kx，将其与抛物线解析式联立成

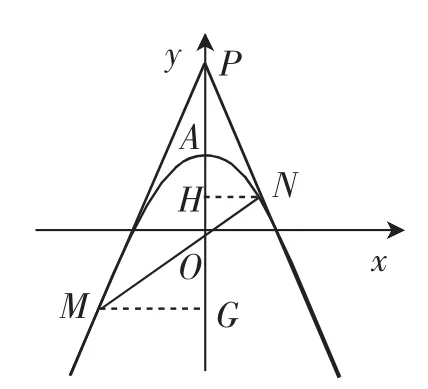
图3

消去y，可得关于x的一元二次方程x2+kx-2=0.

二 、回顾反思与同类链接

同类链接：这道考题最后一问的结构在2016年海南省中考卷第24题曾出现过.

逆向思考：这道考题最后一问的逆向思考问题在2017年湖北中考卷武汉卷第24题曾出现过.这里不妨简要引述一下，便于对比.

考题2：（2016年湖北武汉，第24题）抛物线y=ax2+c与x轴交于A、B两点，顶点为C，点P在抛物线上，且位于x轴下方.如图4，已知直线PA、PB与y轴分别交于E、F两点.当点P运动时，是否为定值？若是，试求出该定值；若不是，请说明理由.

结构认识：如图5，抛物线y=ax2+bx+c的顶点为C，点E、F在抛物线的对称轴上，直线y=n与抛物线交于点A、B.点P是抛物线上一个动点，连接AP，交抛物线的对称轴于E点.

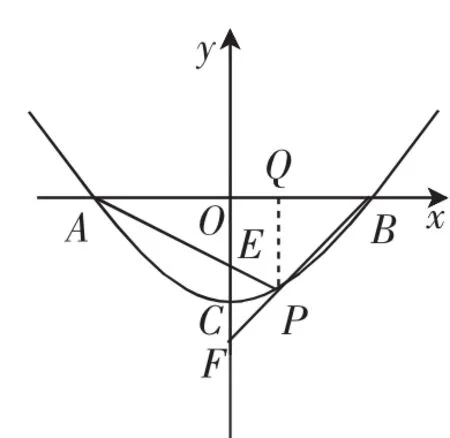
图4

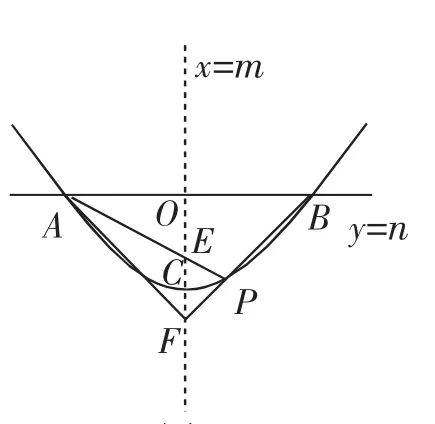
图5

有如下“等价”信息：

①点B、P、F在同一直线上；

②CE=CF；（类似的有OE+EF=2OC）

③∠AFE=∠PFE.

从前面考题1、考题2的求解可知，上述“等价”信息可以“知一推二”.

同类跟进：（2017年江苏泰州某校九上期末试卷）平面直角坐标系xOy中，抛物线的顶点为A（-1，-4），且经过点B（-2，-3），与x轴分别交于C、D两点.如图6，过点A的直线交x轴于点E，且AE∥y轴，点P是抛物线上A、D之间一个动点，直线PC、PD与AE分别交于F、G两点.当点P运动时，EF+EG是否为定值？若是，求出这个定值；若不是，说明理由.

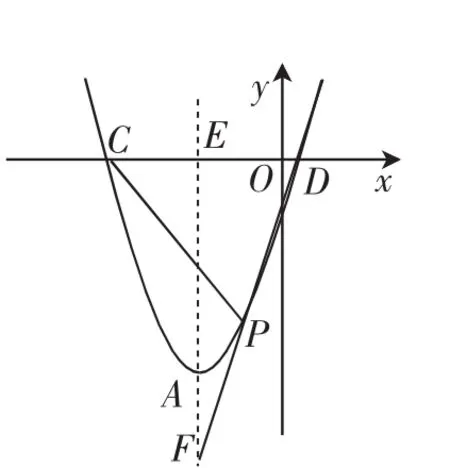
图6

三、教学建议

1.教师要善于归类收集典型考题，并深入研究揭示结构

数学教师的一个重要的日常基本功是解题，应该有自主解题的兴趣与爱好，把平时业余时间常常用来解题是一个优秀数学教师的重要特征之一.当然，仅仅有兴趣解题还不够，还需要在解题之后反思回顾，想清问题结构，并把同类问题归类收集整理到专用的资料夹.笔者的做法是把同类问题演算之后的结构与素材及时保存在电脑上相应文件夹中，文件夹以关键词命名，便于日后检索、调用.比如，本文关注的主题关键词可拟为“抛物线奇异性质”，并把与之相关的考题及演算稿都存入相应的文件夹，有时网络上、文献中的类似资料也可下载保存在一起.

2.组织典型考题讲评时，要引导学生回顾反思提炼结构

教师在组织考题讲评时，可检索自己的素材库把相关类型的问题整理出来，经过编辑加工整合成教学设计，精选一道较简单的考题先讲评，然后变式拓展，边拓展、边追问，让学生在回顾反思中提炼问题结构，加深对同类问题的深刻理解.在讲评之后还可跟进变式再练，不仅是检测听课效果，更主要的是通过“多题归一”训练巩固学生对问题结构的理解.