钢轨波磨区段高速轮轨瞬态滚动接触高频动态特性

于 淼，王卫东，刘金朝

(1.中国铁道科学研究院，北京 100081；2.中国铁道科学研究院 基础设施检测研究所，北京 100081)

钢轨波磨是指新铺设的钢轨在使用一段时间后，在接触表面沿其纵向面出现的波浪形不均匀磨损，具有明显的准周期形态[1]。高速铁路钢轨波磨的波长一般为50～150 mm[2]。当列车运行速度较高时，钢轨波磨易引起轨道—车辆系统的剧烈振动，缩短车辆及轨道部件的使用寿命，增加铁路养护维修费用，严重时对行车安全也是潜在的危害。因此，探究钢轨波磨机理以及明确钢轨波磨引起的轨道—车辆动态响应规律是解决铁路现场波磨问题的关键。

从19世纪末期，国内外开始对钢轨波磨展开研究。波磨成因复杂，与多个因素相关，表现形式也有较大差异。2009年，Grassie S L[3]按照波长固定机理和损伤机理将波磨成因分成了6类，其中，由于Pinned-Pinned共振引起的“响轨波磨”，波长一般为25～80 mm。该类型波磨在直线轨道以及高速铁路曲线区段时有发生，在高速铁路波磨中占主要部分。目前，对波磨成因的研究方法包括现场观测、波磨试验、理论分析、数值仿真等。其中，仿真方法主要分为多刚体动力学仿真、刚柔耦合仿真以及有限元仿真。将轮轨考虑为柔性体时，多用于轮轨自激振动、接触共振及瞬态滚动接触分析。Böhmer[4]利用ABAQUS有限元软件从频域角度研究了塑性变形对钢轨波磨发展的影响。Gómez[5]利用线性模型和“有限条法”对波磨发展趋势进行预测，计算了在各个轮轨固有频率下波磨的预测结果。Correa[6]等利用有限元方法分析了同一转向架不同车轮的位移导纳和模态特性与钢轨波磨的关联关系。陈光雄[7]建立了轮对通过小半径曲线的稳态有限元模型，研究发现蠕滑力饱和时轮轨系统摩擦自激振动将引起曲线钢轨波磨。李霞[8]利用有限元模型研究了轨道振型和共振频率与钢轨波磨的内在关联。以上利用有限元法建模主要从频域角度分析钢轨波磨问题，或利用线性模型对其进行时域分析。Kalker和Groβ-Thebing[9]指出当轮对运动波长与轮轨接触斑长度的比值小于10时需要考虑轮轨非稳态滚动接触问题。钢轨短波波磨是典型的轮轨非稳态滚动接触问题之一。因此，建立轮轨非稳态滚动接触模型是研究高速铁路钢轨短波波磨问题的关键。近几年，赵鑫[10-11]利用三维高速轮轨有限元模型从轮轨瞬态滚动接触角度解释了波磨在出现后进入稳定的现象。

本文针对高速铁路钢轨波磨问题建立轮轨瞬态滚动接触三维有限元模型，考虑轨道—车辆系统耦合作用以及轮轨真实几何，利用隐式和显式相结合方法进行轮轨动态滚动接触计算。进而分析列车高速通过钢轨波磨时的高频动态特性以及列车通过频率对波磨发展趋势的影响，为探究钢轨波磨发展趋势以及防治措施提供理论依据。

1 高速轮轨瞬态滚动接触有限元模型

1.1 模型建立

针对高速铁路轨道—车辆系统，采用了LMA型踏面车轮以及带有波磨区段的无砟轨道。车轮直径为860 mm，钢轨廓形为CN60，设1/40轨底坡。为了避免钢轨两端引起的应力波效应，且考虑轨道扣件整体刚度及阻尼作用，建立的轨道全长为15.21 m，轨枕间距为0.65 m，共24组轨枕，波磨区段长为1 m。设置轮对以第9个轨枕为起点，运行里程约为3.7 m，当轮轨接触由静态到滚动状态时会出现初始激扰，车辆运行速度越高，动态效应越强，所以在波磨区段与车轮初始位置间设置了2.4 m的动态松弛区。为了将本文模型结果与文献[10]相比对，将钢轨波磨波长设为0.08 m，波深0.14 mm，纵向及截面几何参照文献[10]，模型选取的系统结构和材料属性参数基本与其一致，见表1，且均不考虑轮轨横向自由度。文献[10]利用ANSYS/LS-DYNA有限元软件建立了单轮单轨有限元模型，为了更接近实际情况以及下一步开展考虑轮对横向自由度的研究，本文利用ABAQUS有限元软件建立了考虑轨道—车辆系统耦合作用的轨道—轮对模型如图1所示。

利用Hypermesh软件划分轨道—轮对系统有限单元，主要为8节点缩减积分线性实体单元，轮轨初始接触以及钢轨波磨区段采用最小尺寸单元为1.2 mm，整个有限元模型节点约为2.0×106个。由于钢轨波磨主要引起轨道—车辆耦合系统高频振动，车辆一系悬挂以上车辆系统振动频率较低，因此，将一系悬挂以上结构设为施加载荷的质点且能够在垂向自由振动，考虑惯性作用。在车辆系统结构中，轴箱与车轴通过轴承连接，受力较均匀。在有限元模型中一系悬挂由5根弹簧并联模拟，每根弹簧悬挂质点重量为1.6 t，轮对轴重为8 t。钢轨扣件结构由20根弹簧(4排×5列)并联模拟，仅考虑垂向刚度和阻尼，仿真模型中共建立48组扣件系统(一侧钢轨24组)，通过编译脚本程序自动生成。固定CA砂浆底面，轨道两端施加对称边界条件。

表1 模型参数

图1 轨道—车辆系统有限元模型

1.2 计算方法

利用隐式和显式相结合方法模拟高速轮轨瞬态滚动接触过程。隐式算法利用Newton迭代且满足动力学平衡方程，基于面—面接触算法计算轮对在初始位置的轮轨接触状态。初始增量步设为0.1 s，采用自动增量步调整。由于隐式算法是无条件稳定的，所以时间增量相比于显式算法要大一些[12]。但是在解决非线性问题时，由于每1个增量步需要经过多次迭代才能满足给定的容许误差要求，所以计算耗时较长。

轮对动态滚动阶段采用显式积分方法。ABAQUS/Explicit采用中心差分法计算接触问题。对一般的非线性问题，增量开始时需要搜索接触面并判断接触状态。内力和接触力根据上一步的状态进行递推，因此不需要隐式算法的迭代过程。利用该方法进行显式时程积分，计算波磨区段轮轨受力状态。计算过程主要分为4个步骤，具体如下。

步骤1：在t时刻，求出第i个增量步的节点加速度[12]，为

ü(i)=M-1(FP(i)-FI(i))

(1)

式中：u为节点位移；M为节点质量矩阵；FP为外力；FI为内力。

步骤2：对加速度在时域积分。在1个增量步内，加速度假定为恒值，Δt为时间增量，则节点速度为

(2)

步骤3：对速度在时域积分。在1个增量步内，速度假定为恒值，则节点位移为

(3)

步骤4：通过应变变化率计算应变增量dε，从而计算应力σ，然后将由式(5)计算所得的节点内力作为下1个增量步的初始内力，进入下1个增量步计算。

σ(i+1)=f(σ(i)，dε)

(4)

FI(i+1)=BTσ(i+1)

(5)

式中：B为应变矩阵。

1.3 模型验证及对比

隐式与显式算法在计算轮轨接触时有所不同，将静态结果作为初始条件导入动态显式计算时会引入初始激扰。若此时加载轮对初始速度会使初始激扰更加剧烈，延长所需的动态松弛区长度，增加计算时长。为此，在采用隐式算法计算轮轨静平衡后，增加采用显式算法计算轮轨平衡的过程。

将利用隐式算法获得的轨道—车辆系统静态平衡时的结果作为初始条件，由于弹簧状态无法作为初始条件导入，需基于轴重计算设置弹簧预压力。利用显式方法计算轮轨接触达到平衡时的时域过程如图2所示。从图2可以看出：轮轨接触存在初始激扰，当计算时长为0.03 s时，轮对垂向振动加速度已经趋于0，且轮轨垂向接触力基本平稳，约为83.5 kN。因此，将显式方法计算轮轨接触平衡的时长设为0.03 s即可满足计算轮轨平衡的要求。

图2 基于显式算法的轮轨接触平衡过程

设置轮对初始运行速度为300 km·h-1，包括沿纵向的平动速度及绕轴心的转动角速度。为避免轮对在运行中一系悬挂作用点出现偏心情况，需添加一系悬挂载荷质点与轮对作用点在纵向及横向运动方向上的位移等式约束。在不施加牵引扭矩情况下，轮对沿钢轨纵向自由滚动，轮轨瞬态滚动接触力如图3所示。

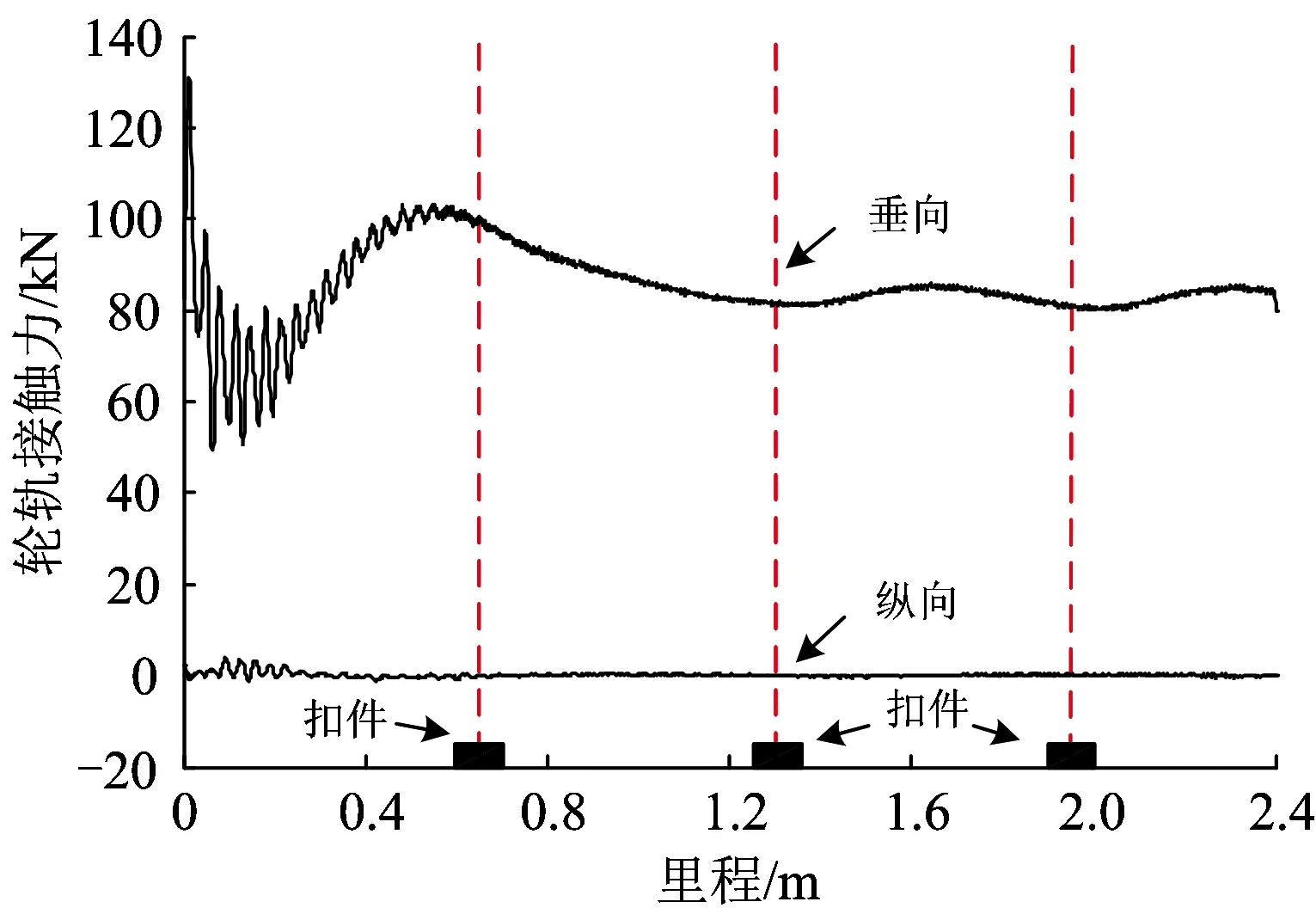
图3 轮轨接触力

从图3可以看出：由于轮对设置了初始运行速度，所以轮轨接触力存在初始高频振动；轮轨垂向接触力和纵向接触力在运行里程为1.2 m左右时收敛趋于平稳；轮轨纵向接触力基本为0，车轮与钢轨接触为纯滚动，扣件对轮轨纵向接触力影响不大；由于轨枕处扣件系统刚度与阻尼作用，离散支撑轨道系统存在固有刚度不平顺，在扣件附近轮轨垂向接触力出现波谷，幅值约为4 kN，且相对于扣件位置存在约0.2π的相位滞后。

达到轮轨接触平稳后的轮对继续沿钢轨向前滚动，在2.4 m处进入钢轨波磨区段，得到光滑钢轨表面(钢轨无波磨)和波磨条件下的轮轨接触力，并与文献[10]结果对比如图4所示。

图4 轮轨垂向接触力对比结果

从图4可以看出：本文轮轨滚动接触仿真模型与文献[10]中轮轨垂向接触力波动的趋势基本一致。从光滑钢轨表面处轮轨垂向接触力可以看出，文献[10]中结果在轮轨接触力平衡时仍存在峰峰值约为5 kN的高频振动，而本文轮轨垂向接触力相对平稳，这是造成文献[10]的钢轨波磨区段轮轨接触力波动大于本文的主要原因之一。由于离散支撑轨道系统存在固有刚度不平顺，在扣件附近光滑钢轨表面轮轨垂向接触力出现波动。文献[10]中考虑了轮对附属部件质量为3.3 kN，因此轮轨垂向接触力均值大于本文结果。同时，由图4还可以看出：对应波磨波峰附近轮轨垂向接触力出现波峰，对应波磨波谷附近轮轨垂向接触力出现波谷；轮轨垂向接触力波峰相对于波磨峰值存在约0.25π的相位超前，进而促使钢轨波磨向车轮滚动方向发展；轮轨垂向接触力在轨枕附近整体振动较大，最大峰值约为126 kN，动静比约为1.5；在轨枕跨间整体振动较小，最小峰值约为109 kN，动静比约为1.3。波磨区段轮轨垂向接触力整体振型与“拍”振类似，可能存在波磨引起的激振力与轨道系统某固有频率相接近的情况，即可能发生了系统共振，形成了时强时弱的信号。为此，下一部分将进一步研究轨道—车辆系统可能存在的共振现象。

2 轮轨瞬态响应分析

2.1 波磨区段列车通过频率分析

我国高速铁路运营速度为200～350 km·h-1，因此，为了研究波磨区段列车通过频率对轨道—车辆系统动态响应的影响，选取列车在100～500 km·h-1运行速度下波磨区段轮轨滚动接触状态进行对比分析。当列车运行速度为v(km·h-1)时，通过波长为λ(m)的波磨区段所对应的列车通过频率fw(Hz)为

(6)

利用式(6)计算可得出列车运行速度为100～500 km·h-1时，波长为0.08 m波磨区段的列车通过频率如图5所示。从图5可以看出：列车的运行速度与通过频率成正比，波长为0.08 m的短波波磨引起轨盗—车辆系统高频振动。

图5 不同速度下钢轨波磨区段列车的通过频率

2.2 钢轨Pinned-Pinned振动分析

钢轨Pinned-Pinned振动是指振型的节点位于轨枕处，钢轨似乎被轨枕处的节点固定，即钢轨在轨枕作用下的周期性固定模态振动形式。在2个轨枕跨中处施加激励，易激发钢轨Pinned-Pinned振型，且频率响应存在1个显著峰值；在轨枕上方施加激励会出现反谐振振型[11]。文献[3]中提出钢轨Pinned-Pinned频率的计算方法，APD Man对其进行了简化，并添加了Pinned-Pinned频率的模态阶数系数n，钢轨n阶Pinned-Pinned频率fp[13]为

(7)

式中：m和EI分别为单位长度钢轨的质量及钢轨的抗弯曲刚度；L为轨枕或扣件间距。

通过现场测试和仿真计算，APD Man进一步提出了更接近实际的Pinned-Pinned频率估算公式，为

fp=10.2L-1.61(EI)0.33m-0.33

(8)

从式(8)可以看出，除去钢轨固有属性外，钢轨Pinned-Pinned振动频率主要与轨枕间距有关，因此，可以考虑通过缩短轨枕间距来提高钢轨Pinned-Pinned振动频率。在本文模型中，L=0.65 m，EI=6.62×106N·m2 [14]，m=60.643 kg·m-1。则由式(7)可得1阶Pinned-Pinned频率的计算结果约为1 228 Hz，由式(8)可得的计算结果约为938 Hz。

对轨道系统有限元仿真模型进行模态计算，获得轨道结构中钢轨垂向Pinned-Pinned振动模态如图6所示，图中放大变形系数为50。

图6 钢轨垂向Pinned-Pinned振动模态

通过模态计算可得钢轨垂向Pinned-Pinned频率为949.43 Hz，波长为扣件间距的2倍，且在2个扣件之间振幅最大，在扣件处振幅为0。仿真所得模态结果即钢轨垂向Pinned-Pinned频率与式(8)的计算结果相接近，因此式(8)可用于估算钢轨Pinned-Pinned频率。无砟轨道扣件间距一般为0.65 m，最小不宜小于0.60 m，由此利用式(8)计算可得高速铁路无砟轨道Pinned-Pinned频率一般约为938～1 067 Hz。结合式(6)可得当列车以270～307 km·h-1速度通过0.08 m左右波长的波磨钢轨时，钢轨会出现Pinned-Pinned共振模态。由于系统存在较大的阻尼，所以即使在共振区域，共振频率的动力放大因数也会较小，轨道—车辆系统动态响应振幅变化不会过于剧烈。

2.3 钢轨Pinned-Pinned振动对轮轨接触力的影响

利用三维轮轨瞬态滚动接触仿真模型，研究钢轨Pinned-Pinned振动对轨道—车辆系统动态响应的影响，包括轮轨垂向接触力和纵向接触力。当不施加牵引扭矩时，轮对为纯滚运动，轮轨纵向接触力为0，因而无法研究钢轨Pinned-Pinned振动对轮轨纵向接触力的影响。所以，当计算动态轮轨滚动接触时，在轮对车轴处施加牵引扭矩，模拟列车牵引过程。模型中轮轨摩擦系数设为0.5，为避免车轮出现打滑现象，则取牵引系数为0.3。利用显式算法计算轮轨接触平衡时的轮轨接触力可求出所要施加的牵引扭矩大小。为了减缓施加牵引扭矩时引起的初始轮轨接触波动，牵引扭矩在轮对初始位置时设为0，然后成线性增加，在轮对滚动0.005 s时达到最大值[10]，即牵引系数为0.3时对应的牵引扭矩值，约为21 500 N·m。之后，牵引扭矩保持不变。在牵引扭矩作用下，列车运行速度如图7所示。

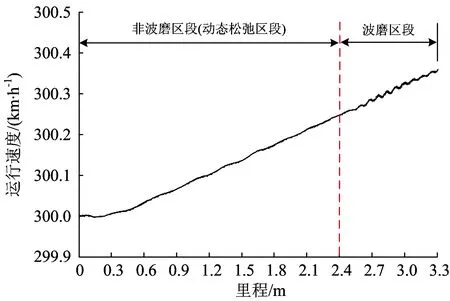
图7 牵引扭矩作用下列车运行速度

从图7可以看出：由于初始阶段牵引扭矩较小，在轮轨摩擦力作用下列车运行速度会略有下降；当牵引扭矩保持最大值不变时，列车运行速度会逐渐增加，且在波磨区段随波磨几何不平顺呈现轻微周期性波动。由于模型中波磨区段长度为1 m，该区段列车运行速度增加不超过0.2 km·h-1，速度变化相对较小，因此，在后文的分析中可忽略牵引扭矩引起的速度改变所带来的影响。

由第1.3部分可知，轮对滚动基本进入稳态后，在通过轨枕上方钢轨时由轨道离散支撑作用引起的刚度不平顺会导致轮轨接触力出现波动。当施加牵引扭矩时，列车以不同速度运行，轮对在未进入钢轨波磨区段前，不同速度下的轮轨垂向接触力如图8所示。

从图8可以看出：低速时轮轨垂向接触力振动收敛较迅速，随着列车运行速度的提高，轮轨垂向接触力初始高频振动将愈发剧烈；在不同运行速度下，列车运行约1.5 m后基本进入平稳状态；当轮对通过2 m附近处轨枕上方钢轨时，轮轨垂向接触力再次出现波动。当运行速度为100 km·h-1时，轮轨垂向接触力波动不明显。随着运行速度的提高，由于轨道—车辆系统刚度和阻尼的作用，扣件附近轮轨垂向接触力出现波动越明显，且轮轨垂向接触力逐渐减小，相对于扣件位置存在相位滞后。

图8 钢轨非波磨区段不同速度下的轮轨垂向接触力

达到轮轨接触平稳后的轮对继续沿钢轨向前滚动，在2.4 m处进入钢轨波磨区段。在牵引扭矩作用下，列车以不同速度运行时波磨区段轮轨垂向接触力如图9所示。

图9 钢轨波磨区段不同速度下的轮轨垂向接触力

从图9可以看出：当列车运行速度为100 km·h-1时，钢轨波磨区段轮轨垂向接触力随波磨几何不平顺基本成周期等幅振动，受轨枕处扣件支撑作用影响较小。对应波磨波峰附近的轮轨垂向接触力出现波峰；对应波磨波谷附近的轮轨垂向接触力出现波谷。轮轨垂向接触力波峰相对于波磨峰值存在相位超前，进而促使钢轨波磨向车轮滚动方向发展。随着列车运行速度的提高，轮轨垂向接触力振幅整体呈上升趋势。当速度为200～300 km·h-1时，轮轨垂向接触力最大值出现在轨枕上方附近，2个轨枕跨中处迅速减小；当速度为400～500 km·h-1时，轮轨垂向接触力最大值出现在2个轨枕之间中后部分，在轨枕上方较小，与前面提到的钢轨离散支撑规律一致，是由于轨枕处扣件系统刚度及阻尼作用。当速度为300 km·h-1时，对应列车通过频率为1 042 Hz，相对接近于钢轨1阶垂向Pinned-Pinned振动频率，轮轨垂向接触力出现“拍”振形式，轨道—车辆系统出现了Pinned-Pinned共振。由于轨道系统存在较大的阻尼，所以即使在共振区，共振频率的动力放大因数也会相对较小，振幅变化不会过于剧烈。

当列车运行速度分别为300和400 km·h-1时，利用Wigner-Ville分布对轮轨垂向接触力进行时频分析，并进行500 Hz高通滤波后的结果如图10所示。

图10 轮轨垂向接触力时频图

从图10可以看出：当列车运行速度为300 km·h-1时，主频约为1 042 Hz的轮轨垂向接触力振动能量主要集中在2.6 m处以及3.25 m处的轨枕上方附近，Pinned-Pinned共振将造成轮轨垂向接触力较大波动，会加速扣件系统伤损或疲劳断裂；当列车运行速度为400 km·h-1时，主频约为1 389 Hz的轮轨垂向接触力振动能量主要集中在2个轨枕之间中后部，约3 m附近。

列车以不同速度运行时轮轨纵向接触力如图11所示。

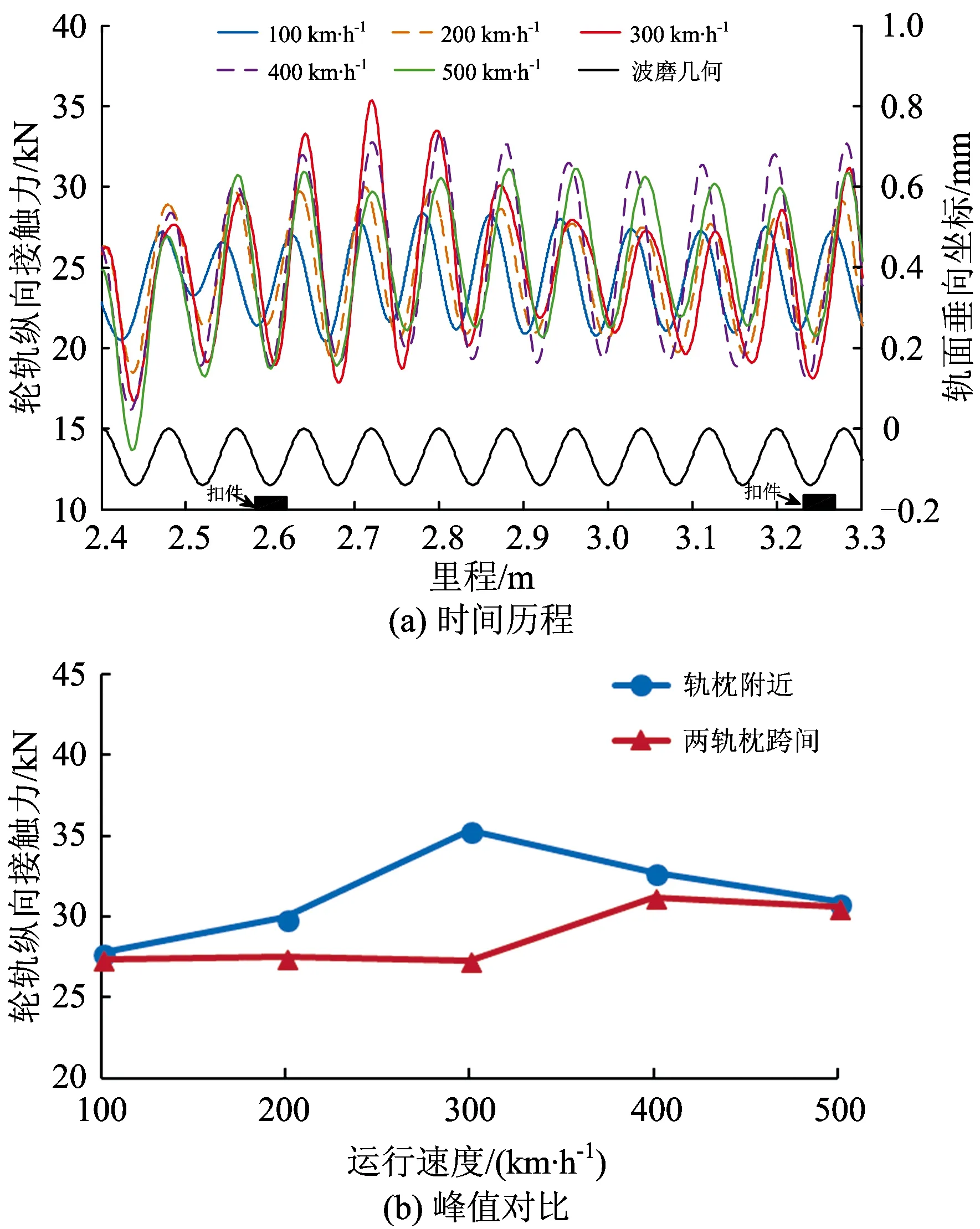
图11 不同速度下钢轨波磨区段的轮轨纵向接触力

从图11可以看出：列车以不同速度通过钢轨波磨区段时，轮轨纵向接触力随波磨几何不平顺呈周期性波动，对应波磨波峰附近的轮轨纵向接触力出现波峰，对应波磨波谷附近的轮轨纵向接触力出现波谷，且相位略有差异。当速度为300 km·h-1时，轨枕上方附近的轮轨纵向接触力明显大于其他速度结果，且“拍”振形式较明显，即与钢轨Pinned-Pinned振动发生了共振，轮轨纵向接触力最大峰值主要出现在轨枕上方后0.2 m之内，约为2个轨枕跨间最小峰值的1.3倍。由于轨道系统阻尼较大，共振现象不会过于剧烈。对比图9和图11可以看出，Pinned-Pinned共振对轮轨纵向接触力影响相比于垂向接触力更加明显。

在钢轨波磨区段，车轴处施加的牵引扭矩载荷为定值，是由牵引系数0.3计算获得。而当列车通过钢轨波磨区段时，由于轮轨非稳态滚动接触作用，当牵引扭矩为定值时，牵引比(轮轨纵向接触力与垂向接触力的比值)[3]出现了波动。计算速度为300 km·h-1时波磨区段的牵引比如图12所示。

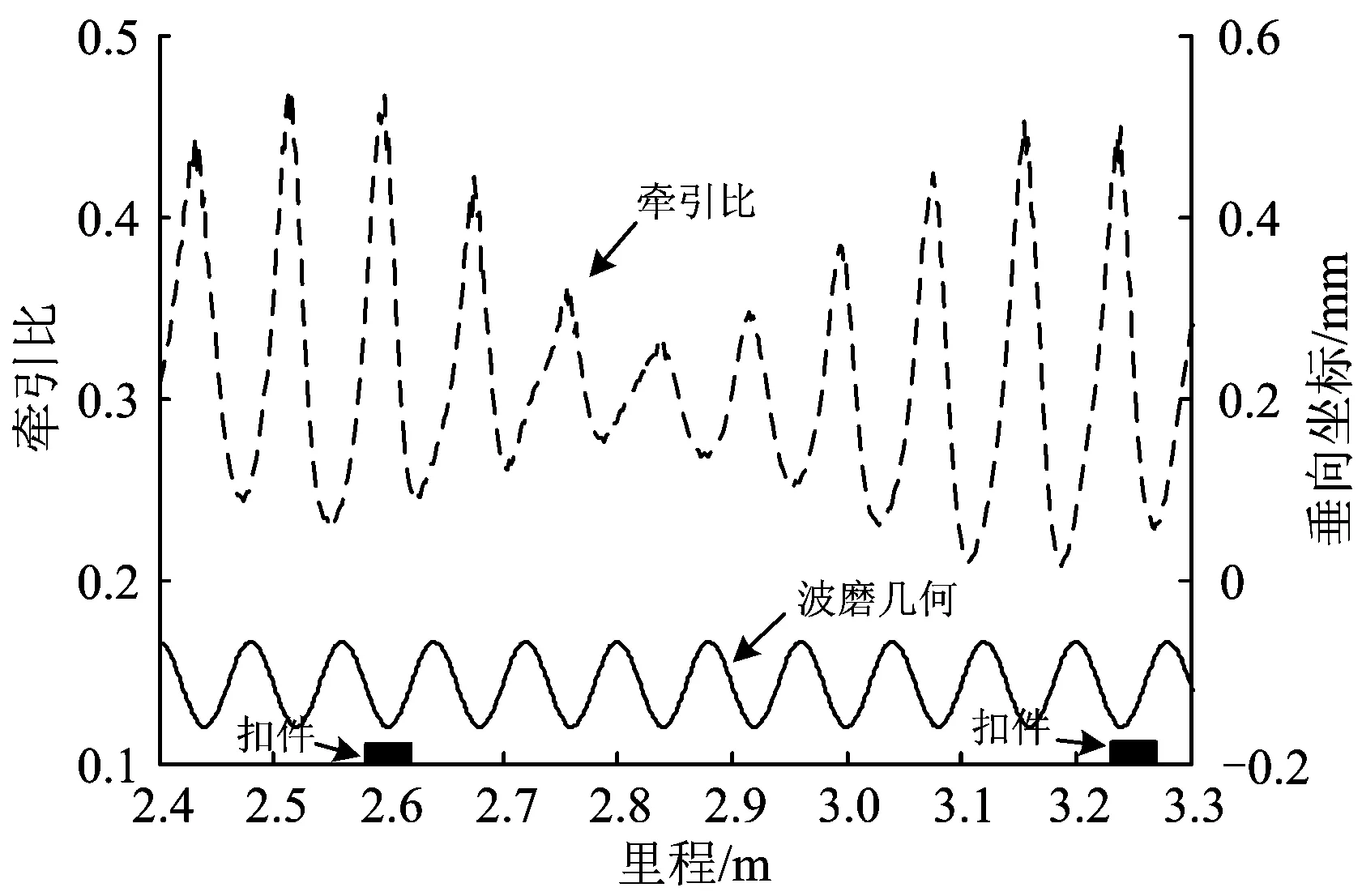
图12 波磨区段牵引比

从图12可以看出：波磨区段牵引比出现明显波动，波动范围在0.20～0.48之间，波峰均未超过轮轨摩擦系数0.5，说明轮轨接触既没有发生纯滚也没有出现全滑动现象。轮轨接触出现了周期性黏滑振动，进而导致钢轨表面的不均匀磨耗[1]。与轮轨垂向接触力和纵向接触力分布不同，牵引比与波磨几何不平顺基本上为反相位，对应波磨波谷附近的牵引比出现波峰；而对应波磨波峰附近的牵引比出现波谷。波磨区段的牵引比在轨枕附近整体波动较大，最大峰值约为0.47，接近于轮轨摩擦系数0.5，则波磨波谷处轮轨接触斑内滑动区与黏着区的比值较大，将会加剧波磨波谷处滑动磨损，而波磨波峰处牵引比较小，作用不明显。牵引比在2个轨枕跨间整体波动较小，最小波峰约为0.33。因此，列车通过波磨区段时，在牵引扭矩作用下，轮轨接触存在周期性黏滑振动，当轨道—车辆系统出现Pinned-Pinned共振时，会促使轨枕附近钢轨波磨波谷处的滑动磨损。

3 结论及展望

(1)列车以不同速度通过钢轨波磨区段时，轮轨垂向接触力和纵向接触力随波磨几何不平顺呈周期性波动，相位略有差异，对应波磨波峰附近的轮轨接触力出现波峰，对应波磨波谷附近的轮轨接触力出现波谷；而牵引比波动与波磨几何不平顺基本呈现反相位。

(2)当列车通过波磨区段所对应的通过频率与轨道Pinned-Pinned频率相近时引起系统共振，轮轨接触力出现“拍”振特性；轮轨接触力在轨枕附近整体波动较大，在2个轨枕跨间整体波动较小，会加速钢轨扣件伤损。

(3)列车通过波磨区段时，在牵引扭矩作用下，轮轨接触存在周期性黏滑振动。当轨道—车辆系统出现Pinned-Pinned共振时，波磨区段的牵引比在轨枕附近整体波动较大，波磨波谷处牵引比接近于轮轨摩擦系数，将会加剧波磨波谷处滑动磨损，加快波磨的发展。

(4)由于本文主要针对直线轨道钢轨波磨问题，且两侧钢轨采用相同波磨几何不平顺，因此轮轨横向蠕滑作用较小，同时，为了更好地与文献[10]结果相比对，本文在建立高速轮轨非稳态滚动接触模型时约束了轮轨横向自由度。在后续工作中，解决曲线波磨问题以及两侧钢轨存在不同波磨几何不平顺时将进一步研究横向蠕滑对钢轨波磨形成及发展的影响。