深圳典型潜水地层地铁车站基坑降水引起水位变化机理的试验研究

杨清源，赵伯明，孙风伯，赵天次

(1.北京交通大学 城市地下工程教育部重点实验室，北京 100044;2.北京交通大学 土木建筑工程学院，北京 100044)

近些年，随着地下轨道交通系统的开发和建设，地铁车站深基坑数量逐渐增多。基坑开挖深度的增加，导致降水的时间会更长，降水程度增大，从而对周围地表变形的影响也愈加突出。目前，国内外学者在基坑降水引起周围地表变形研究方面取得了一定成果[1-6]，这些成果中均采用Dupuit理论的降水曲线[7]划分由基坑降水导致的基坑外土层疏干区。但实际上，当含水层厚度较大，常因经济或技术条件限制，基坑地连墙无法将基坑内外的含水层完全隔离，基坑内降水井也主要为不完整井，因此基坑内降水会对井底部以下一定深度的地下水产生影响，同时地连墙底部会出现坑外地下水绕渗现象，引起基坑外地连墙附近地下水发生水平和竖直方向运动[8]，导致坑外实际降水曲线与Dupuit理论降水曲线的形式存在差异，进而影响基于Dupuit理论降水曲线计算得到的地表沉降的准确性。可见，揭示不完整井有效影响深度的变化规律以及地连墙底部出现地下水绕渗现象引起基坑外水位变化的机理，具有重要实际意义。

本文基于深圳典型潜水地层，以深圳某地铁车站基坑工程为背景，通过室内模型试验，结合理论分析，对不完整井降水有效影响深度变化规律和计算方法以及地连墙底部出现地下水绕渗引起坑外的水位变化机理进行研究。

1 室内模型试验

1.1 工程背景

模型试验以深圳某地铁车站基坑工程为背景，基坑所在区域的地层从上到下依次为粉质黏土层、砾质黏性土层、全风化花岗岩层和强风化花岗岩层。该地层为典型的潜水地层，地下水位为0.70～4.60 m。地层与降水有关的物理力学参数见表1。

地铁车站基坑长度为365 m，宽度为25 m，地连墙埋深为32 m，基坑内降水井按照车站基坑长边向每15 m布置2个，共设置48口井，如图1所示，图中W-1等和E-1等分别为降水井的编号。考虑试验场地条件限制以及试验研究重点是基坑内不完整井降水引起基坑外水位变化的机理，在满足降水井与基坑地连墙间距以及降水井相互间距与实际工程的几何相似比的基础上，选取中间位置的部分车站基坑结构开展模型试验研究。

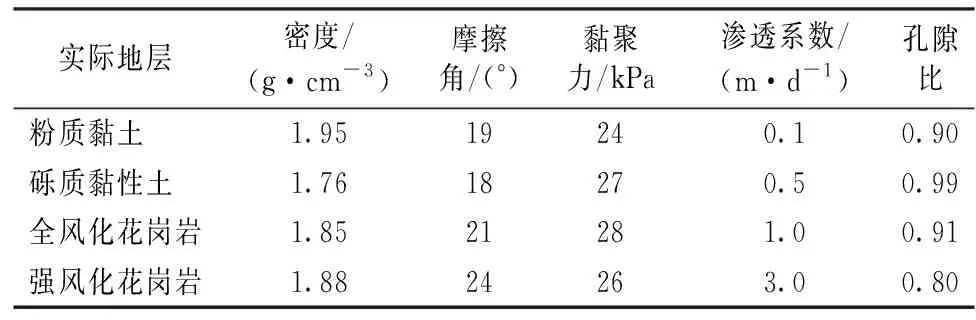
表1 地层的物理力学参数

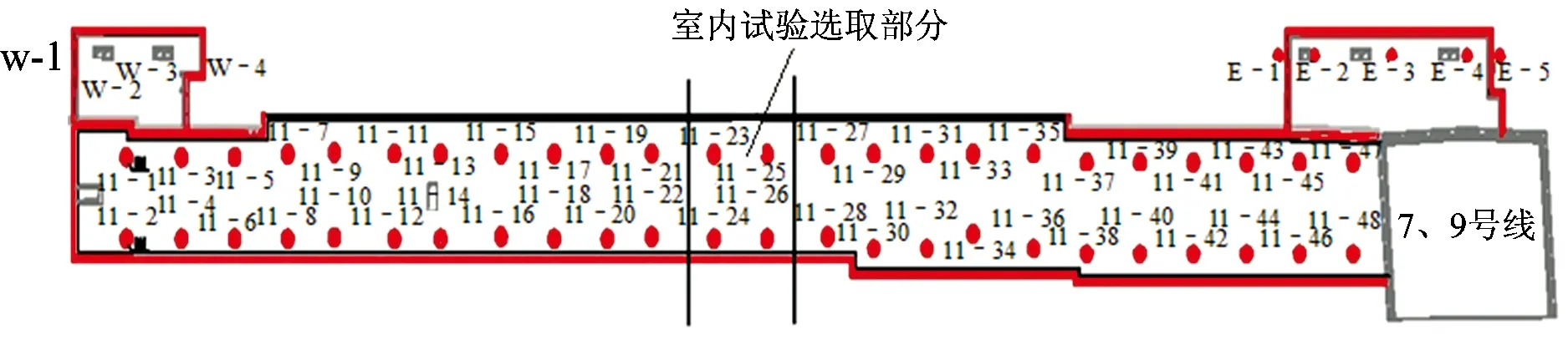
图1 基坑工程降水井布置图

1.2 相似比及地层材料

取几何相似比Cl=1∶50，密度相似比Cρ=1∶1，重力加速度相似比Cg=1∶1。基于这3种物理量的相似比，通过传统量纲分析法[9]可推导出各相关物理力学参数的相似比，分别为摩擦角的相似比Cφ=1∶1，渗透系数的相似比Ck=1∶7，孔隙比的相似比Ce=1∶1，黏聚力的相似比Cσ=1∶50。

模型试验的原材料选用40目精制石英砂、150目和300目石英砂粉[10]，根据表1中4层实际地层的参数以及对应的相似比，分别按照不同的质量配比将原材料混合制成模型中的4种相似地层材料，通过测量得到相似地层的物理力学参数，见表2。考虑每次试验周期较长，选取均一砾质黏性土和全风化花岗岩分别作为相似地层材料进行试验。

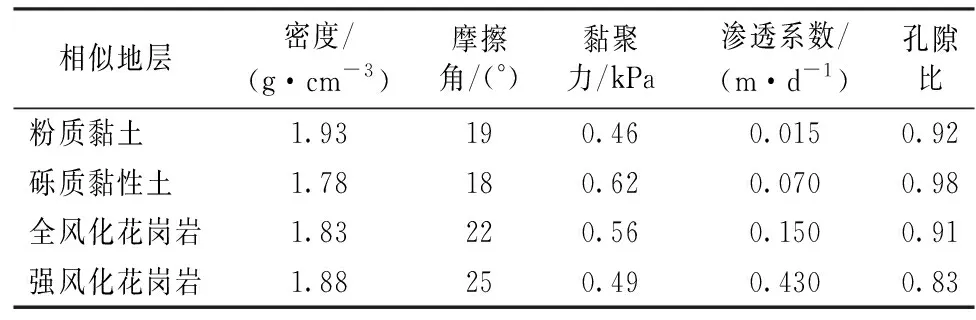
表2 相似地层的物理力学参数

1.3 地下连续墙

根据该基坑工程的设计方案可知，地下连续墙(简称为地连墙)的厚度为1 000 mm，采用钢筋混凝土砌成，钢筋混凝土的弹性模量为35 GPa，泊松比为0.167。由分离相似设计理论[11]，模型中地连墙选用有机玻璃板制成，有机玻璃的弹性模量为3.1 GPa，泊松比为0.25。根据抗弯刚度相似等效原则，确定模型中有机玻璃板的厚度为11 mm。

1.4 试验箱和抽水系统

试验箱的长×宽×高为2.0 m×1.8 m×1.2 m，四周均有补水箱，补水箱与降水区域之间采用带微小孔洞的隔板相隔。隔板厚度为5 cm，隔板开孔率为48%，大于试验地层最大孔隙率44%，故可通过调节隔板的开孔数量，使隔板开孔率与地层孔隙率一致，满足对试验地层稳定渗流供水，形成定水头边界条件。同时在补水箱中加入中空圆柱状支撑，以保证在整个试验过程中隔板不发生变形。抽水系统由抽水泵、降水井管、抽水管和抽水量控制阀门组成，其中降水井管采用外径为20 mm的PVC线管制成。

1.5 测点布置

模型试验测点布置如图2所示，其中在距5#降水井左侧0.05 m处设置测点1，在距1#降水井右侧0.05 m处设置测点2，分别在测点1和测点2处，从地表开始沿模型箱深度方向每隔0.05 m布置1个孔隙水压计，直至模型箱底部。在距地连墙外侧0.10 m处设置测点3，在测点3外每隔0.15 m设置1个测点，直至测点8，在测点3—测点8处沿模型箱深度方向分别于埋深0.07，0.22，0.37，0.52 m布置1个孔隙水压计。测点1和测点2主要对不完整井有效影响深度进行监测，测点3—测点8主要对基坑外与地连墙不同距离孔隙水压变化进行监测。

图2 测点布置图(单位：m)

1.6 试验工况

共设置6种工况，详见表3，每种工况下的降水深度均为0.1，0.2，0.3，0.4，0.5 m。

表3 工况设置

1.7 试验实施步骤

以工况1为例，试验实施步骤如下，其他工况试验实施步骤均与之相似，不再详细论述。

将制作的砾质黏性土土样由人工用铁锹缓缓填入箱体中。每填铺10 cm厚度时进行地层夯实，以保证土层的物理参数稳定。当填筑至试验仪器、基坑地连墙和降水管埋置深度时，将箱底排水管均连接到高处水箱，通过高处水箱向试验箱内注水，注水速度可通过箱底排水管口的阀门进行调节，保证流速平稳，且不易过快，使土层自下而上饱和，土层内饱和后会产生一定的沉降变形，则需要继续填入土样，经过1～2次饱和与补填之后，方可进行监测仪器的埋设和土样的继续填入，直至装填至试验要求的高度1.1 m。试验箱中土层固结时四周水箱和降水试验区域的水位均应保持在1.1 m，直至土层地表沉降观测点的位移计读数变化小于0.001 mm·d-1时表明土层的固结基本完成，此时达到模型试验的初始状态。

为保证降水过程中降水井内水位始终为试验所需的降深，每次降水试验前均应将抽水管的水头固定于5#降水井内指定降水深度(0.1，0.2，0.3，0.4，0.5 m)的位置。

当降水井过滤器埋深相对较浅，即l/2<0.3m0(其中，l为降水井过滤器长度，m；m0为降水井过滤器中点到隔水底板的距离，m)时，采用式(1)所示的巴布什金潜水不完整单井涌水量计算公式[7]进行计算。

(1)

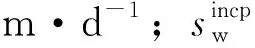
指定降水深度分别为0.1，0.2，0.3，0.4，0.5 m时，由式(1)计算得砾质黏性土地层的理论涌水量分别为0.004，0.008，0.013，0.019和0.026 m3·d-1。试验选用的抽水泵最大抽水量可达5.76 m3·d-1，通过调节抽水管与水泵之间的连接阀门，使抽水量大于或等于涌水量，保证降水井内水头高度始终为所需要的高度。

抽水开始后，始终保持四周水箱的水位为1.1 m，同时观测和采集不同埋深处孔隙水压计的读数，当孔隙水压计读数变化均小于0.001 kPa时认为降水达到稳定，可再继续抽水1 h后关闭抽水泵，整个抽水试验结束。

2 不完整井有效影响深度试验结果分析及理论计算

2.1 不完整井有效影响深度试验结果分析

分别整理6种工况下降水前和降水稳定后的不同埋深孔隙水压变化曲线，如图3所示。以图3(a)为例，当降水深度为0.1 m时，自地层埋深为0.2 m开始，随着地层埋深的增加，降水稳定后的孔隙水压变化曲线与降水前重合，表明该条件下的有效影响深度为0.2 m。以此类推，可得到6种工况下不同埋深时的有效影响深度，见图3。

由图3可知：不完整井基坑内降水有效影响深度大于基坑外，当其他条件相同时，基坑内不完整井有效影响深度是基坑外的平均1.18倍，这是由于基坑内降水地连墙底部出现地下水绕渗现象，绕渗作用增大了不完整井的有效影响深度；基坑内双井同时降水有效影响深度大于单井降水，基坑内双井同时降水有效影响深度是单井降水的平均1.12倍，这是由于群井效应导致绕渗作用增大，进而对有效影响深度的影响增大。

图3 不同工况下不同埋深时的孔隙水压变化曲线及其有效影响深度

2.2 不完整井有效影响深度计算公式推导

以巴布什金潜水层完整井和不完整井涌水量计算方法[7]为基础，结合刘俊龙[12]等将潜水不完整井等效为潜水完整井思路，推导不完整井有效影响深度计算公式。由于深圳典型潜水地层从上到下渗透系数逐渐增大，底部为强风化花岗岩地层，渗透系数最大，地层下部不存在弱透水层，故理论计算可忽略弱透水层本身释水的情况。巴布什金潜水层不完整单井涌水量计算公式见式(1)，完整单井涌水量计算公式[7]为

(2)

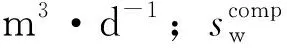
将不完整井等效为与其水位降深及涌水量完全相等的完整井，即

(3)

Qcomp=Qincp

(4)

(5)

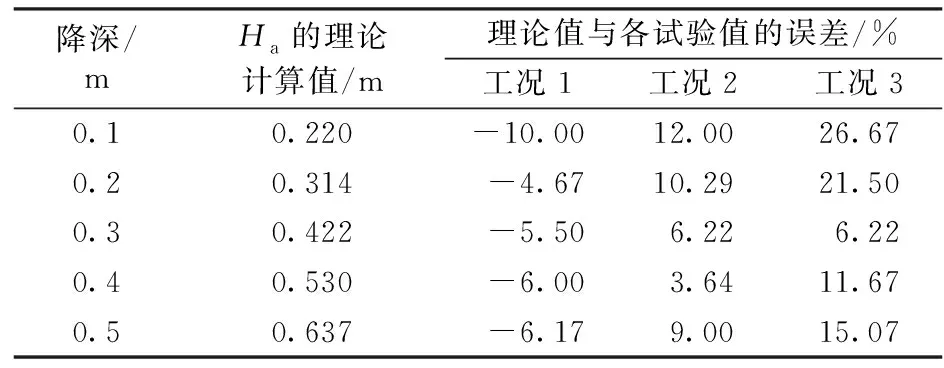
对于砾质黏性土和全风化花岗岩这2种相似地层，针对不同降深，根据式(5)，利用Matlab软件可以近似计算得到Ha。因不完整井与其水位降深及涌水量完全相等的完整井等效，所以等效完整井的含水层厚度Ha，就是不完整井的有效影响深度。同时计算Ha与各工况试验值的误差，结果见表4和表5，其中，与各工况试验值的误差=[(试验值-理论计算值)/试验值]×100%。

表4砾质黏性土相似地层中Ha的理论计算值及其与试验值的误差

降深/mHa的理论计算值/m理论值与各试验值的误差/%工况1工况2工况30.10.220-10.0012.0026.670.20.314-4.6710.2921.500.30.422-5.506.226.220.40.530-6.003.6411.670.50.637-6.179.0015.07

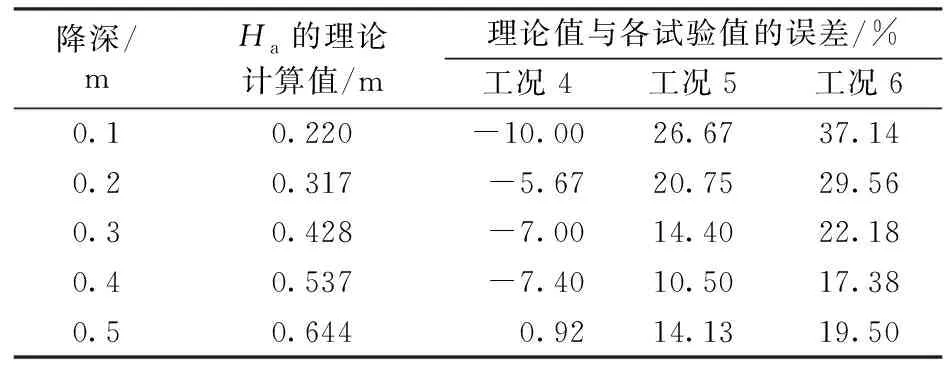
表5全风化花岗岩相似地层中Ha的理论计算值及其与试验值的误差

降深/mHa的理论计算值/m理论值与各试验值的误差/%工况4工况5工况60.10.220-10.0026.6737.140.20.317-5.6720.7529.560.30.428-7.0014.4022.180.40.537-7.4010.5017.380.50.6440.9214.1319.50

从表4和表5可知：理论计算值与工况1、工况4试验值误差相对较小，与工况2、工况3、工况5、工况6的试验值误差相对较大，且均小于试验值。可见，式(5)更适用于单井基坑外不完整井有效影响深度的计算，而运用于基坑内时需乘以放大系数。从2.1节试验结果可知，基坑内不完整井有效影响深度是基坑外的平均1.18倍，基坑内双井同时降水有效影响深度是单井降水的平均1.12倍。因此，基坑内单井有效影响深度理论值可由式(5)理论计算值乘以放大系数1.18得到；基坑内双井降水不完整井有效影响深度理论值可由式(5)理论计算值乘以基坑内影响放大系数1.18，再乘以双井降水影响放大系数1.12得到。实际地铁车站基坑大多均为狭长形，降水井与基坑长边地连墙的距离大多均为5 m(即模型试验中的0.1 m)，且沿宽度方向基坑内多为单井或双井降水，故得到的放大系数满足实际需要。

3 基坑外孔隙水压变化试验结果及降水曲线方程

3.1 基坑外孔隙水压变化试验结果

整理分析工况2降深0.5 m试验中测点3—测点8孔隙水压监测数据，得到基坑外不同埋深孔隙水压时程变化曲线，如图4所示。

由图4可得降水稳定后砾质黏性土相似地层不同埋深水位变化曲线，如图5所示。采用同样方法，由工况4也可得到全风化花岗岩相似地层不同埋深水位变化曲线，如图6所示。

从图5和图6可看出：降水稳定后在地连墙埋深范围内，基坑外土层中水位变化随埋深的增加而增大，同时由于水位变化曲线形式与降水曲线形式完全一致，由水位变化曲线形式可知基坑外降水曲线形式为“先下凹再上凸”型，该线型与潜水层Dupuit降水曲线“类抛物线”型[7]有较大不同。因此采用曲线拟合方法对基坑外降水曲线进行拟合，以得到该曲线方程。

3.2 降水曲线方程拟合

根据图5和图6中不同埋深基坑外水位变化曲线形状和趋势，选取的拟合函数为

(6)

式中：y为地连墙外距离为x处土层的含水厚度；

图4 砾质黏性土地层不同埋深基坑外孔隙水压时程变化曲线

A1，A2，x0和p为拟合参数。

将图5和图6中x和y的试验值分别代入式(6)，可得基于砾质黏性土和全风化花岗岩相似地层拟合函数中各参数的值，详见表6和表7，表中R为相关系数。

图5 砾质黏性土地层不同埋深基坑外水位变化曲线

图6 全风化花岗岩地层不同埋深基坑外水位变化曲线

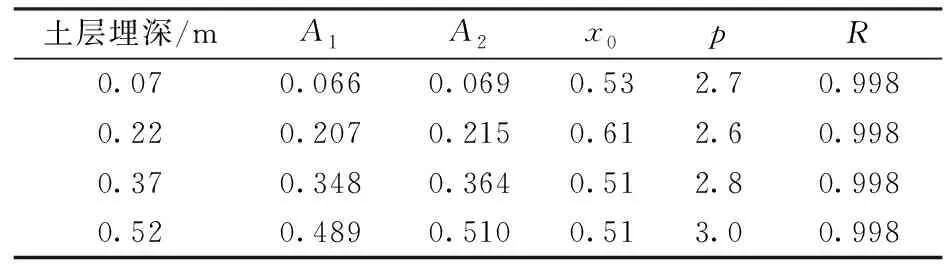
土层埋深/mA1A2x0pR0.070.0660.0690.532.70.9980.220.2070.2150.612.60.9980.370.3480.3640.512.80.9980.520.4890.5100.513.00.998

表7 全风化花岗岩地层拟合函数的参数值

(7)

由式(7)可知，影响地连墙外降水曲线变化的物理量主要有H，hw,k和Ha，如图7所示，其在试验中的取值分别见表8和表9。

图7 某土层降水曲线示意图

土层埋深/mhw/mH/mk/(m·d-1)Ha/m0.070.0660.070.070.750.220.2070.220.070.750.370.3490.370.070.750.520.4900.520.070.75

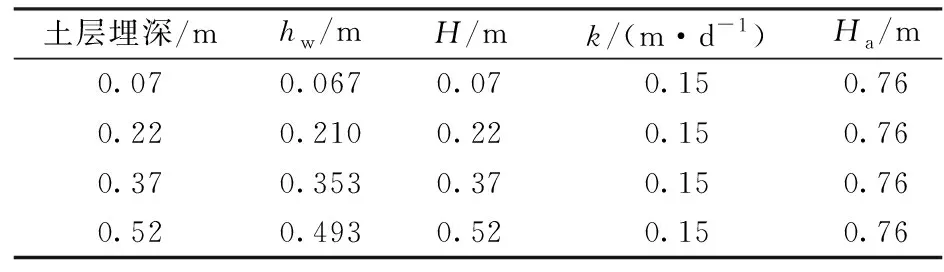
表9 全风化花岗岩地层主要物理量值

将拟合参数替换为与之相关的物理量，式(6)可以改写为

(8)

式中：h为降水稳定后与地连墙间距离为x处土层的含水厚度，m。

分别对砾质黏性土、全风化花岗岩地层，采用式(8)计算得到不同埋深时的降水曲线，并将其与试验降水曲线进行对比，如图8和图9所示。

图8 不同埋深降水曲线对比

由图8和图9可看出：本文理论计算结果与试验结果均明确描述了由于地连墙底部绕渗作用从地连墙外侧开始基坑外降水曲线呈先下凹再逐渐上凸的曲线形式，而由文献[7]可知，潜水层稳定流Dupuit降水曲线未考虑绕渗作用影响，从地连墙外侧开始基坑外降水曲线始终为类上凸抛物线形式，故本文理论和试验结果与实际情况更相符。同时理论计算降水曲线与试验降水曲线基本吻合，说明由式(8)计算得到的降水曲线能较准确描述基坑外降水趋势。

图9 不同埋深降水曲线对比

4 理论方法的验证

以图1所示的地铁车站基坑为工程实例，采用软件ABAQUS，建立三维流固耦合有限元模型，模拟实际潜水层基坑内降水有效影响深度及降水引起坑外水位变化，同时采用理论方法计算实际潜水层基坑内降水有效影响深度及降水引起坑外水位变化，将理论计算结果与数值模拟结果进行对比，以验证理论方法的正确性和合理性。

4.1 基本假定

首先做以下假定：降水过程中各土层应力应变关系符合修正剑桥本构理论，地连墙符合线弹性本构理论；地下连续墙与土体之间的接触面服从理想弹塑性本构关系；初始地下水位位于地表，土层均为饱和土。

4.2 有限元模型和土层参数

基坑简化及降水井分布示意图如图10所示。根据图10，在土体的四周侧向边界设置水平方向位移约束和水头在地表的常水头补给边界，在土体的底面设置水平方向和竖直方向位移约束和不透水边界。设置drainage-only flow边界条件于地表和降水井以模拟实际的潜水降水过程[13]。

图10 基坑简化及降水井分布示意图(单位：m)

土体均采用三维8节点孔压单元(C3D8P)，地连墙采用三维8节点非协调单元(C3D8I)，对于土与地连墙的接触面，极限剪切滑移量γcrit和摩擦系数μ分别设置为5 mm和0.3[14-15]。模型采用过渡网格实现模型网格中心加密，四周不加密，以有效节省计算时间，基坑三维有限元模型和网格简图如图11所示。根据土工试验得到主要土层修正剑桥模型参数，见表10。

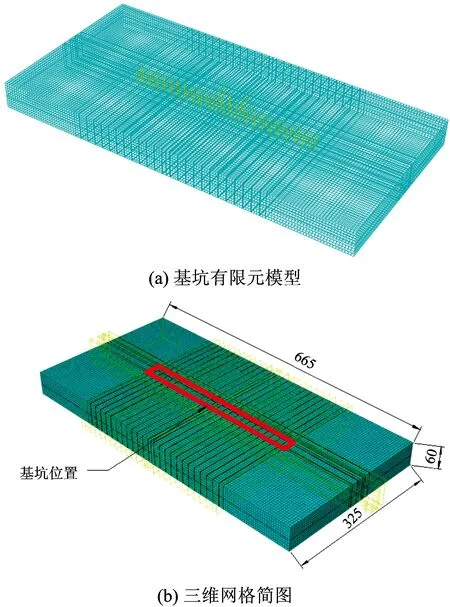
图11 基坑三维有限元模型和网格简图(单位：m)

土层埋深/m重度/(kN·m-3)水平渗透系数/(m·d-1)竖直渗透系数/(m·d-1)压缩系数回弹系数临界状态应力比压缩模量/MPa孔隙比泊松比粉质黏土 0～7.519.50.10.10.022 00.005 20.4708.030.900.32砾质黏性土 7.5～15.017.60.50.50.017 10.004 20.8778.870.990.31全风化花岗岩15.0～22.518.51.01.00.010 10.003 60.97516.050.910.23强风化花岗岩22.5～60.018.83.03.00.010 70.003 31.40414.770.810.23

4.3 测点布置及降水步骤

基坑降水分区及测点布置如图12所示，整个基坑分为降水Ⅰ区和降水Ⅱ区，降水时先对降水Ⅱ区进行分层(共分4层，第1层至第4层)降水并降至指定深度，再对降水Ⅰ区进行分层(共分4层，第1层至第4层)降水降至指定深度。在基坑内中心处设置测点A，在距地连墙外侧5 m处设置测点B，在地连墙中线外侧设置监测断面2-2，每隔1 m取1个测点。测点A主要对数值模拟中基坑内有效影响深度进行监测，测点B主要对现场监测和数值模拟中坑外水位时程变化监测，监测断面2-2主要对数值模拟中基坑外与地连墙不同距离水位降深进行监测。

图12 基坑降水分区及测点布置(单位：m)

基坑指定降水深度为21 m，实际降水过程模拟步骤见表11。

表11 实际降水过程模拟步骤

4.4 有限元模型验证

为忽略基坑开挖对水位变化的影响，数值模拟基坑开挖前降水Ⅱ区第1层(降深5 m)降水引起的水位变化，选取降水Ⅱ区第1层(降深5m)降水过程中测点B现场监测数据和数值模拟数据，绘制水位变化时程曲线，如图13所示。从图13可看出：数值模拟值与现场监测值近乎吻合，说明数值模拟的坑外水位变化值与现场监测值相合性较好，从而验证了数值模拟的准确性。

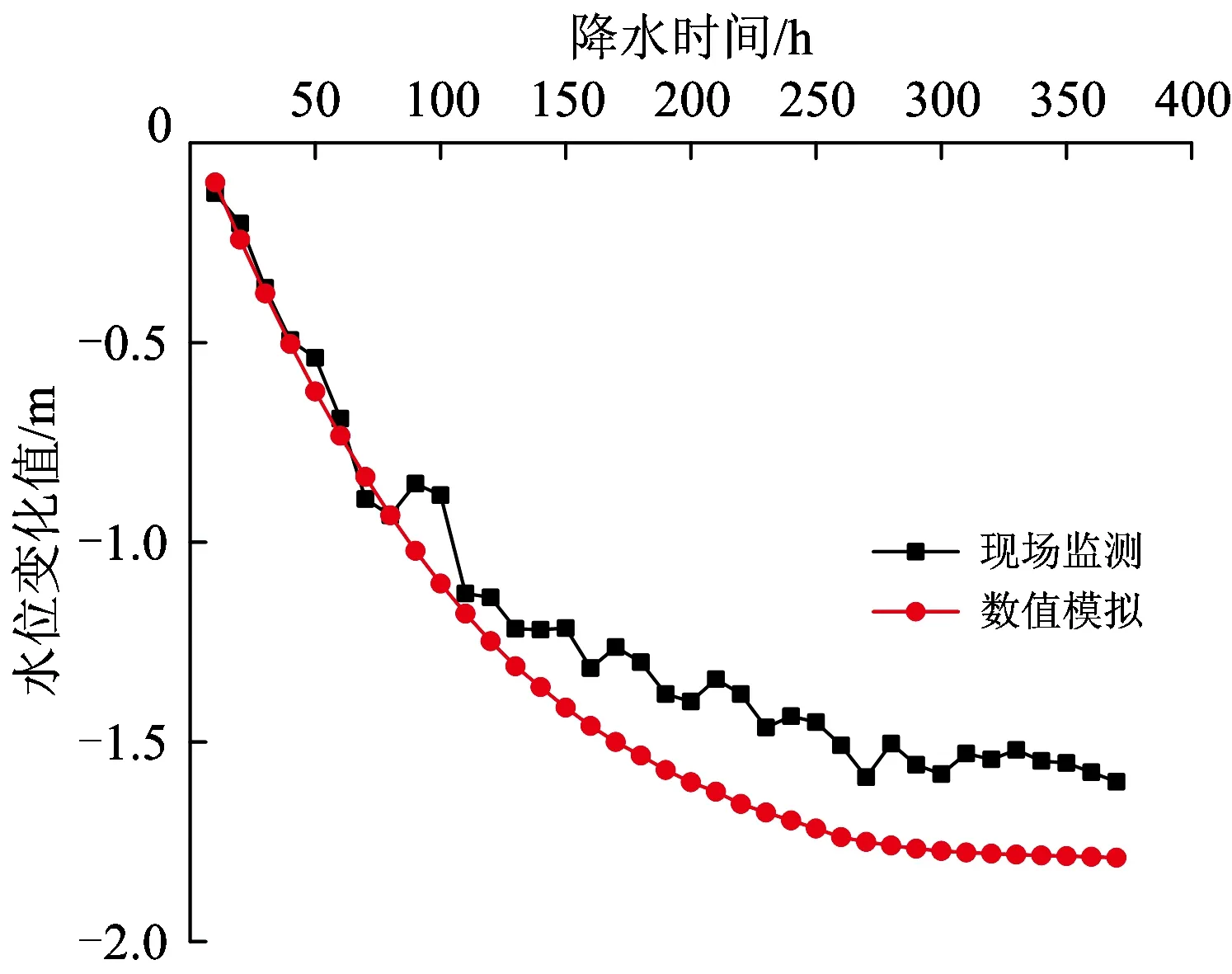
图13 测点B处水位变化时程曲线对比

4.5 理论计算结果与数值模拟结果的对比

4.5.1 有效影响深度

选取图12中基坑内中心测点A，首先，数值模拟降深21 m并且稳定后不同深度处的孔隙水压，绘制孔隙水压变化曲线如图14所示，由此得到基坑有效影响深度为40 m。

图14 测点A处孔隙水压变化曲线

然后，采用本文提出的理论计算方法进行计算。由于深圳地区潜水典型成层地层最小渗透系数与最大渗透系数相差不超过30倍，且地层从上到下渗透系数逐渐增大，不存在强弱透水层交替出现的情况，为方便计算，将不同地层等效为成层地层，成层地层的渗透系数采用等效渗透系数[7]，等效渗透系数计算公式为

(9)

式中：k为成层地层的等效渗透系数，m·d-1；ki为第i层土层的渗透系数，m·d-1；Si为第i层土层的厚度，m。

根据表10中的数据，采用式(9)计算得到成层地层等效渗透系数为2.4 m·d-1，进而采用式(5)计算得潜水层基坑内不完整井指定降深21 m时最大有效影响深度为42 m。

可见理论计算值与数值模拟值误差较小，验证了该理论计算公式的准确性。

4.5.2 水位降深曲线

选取图12中的监测断面2-2，数值模拟降深21 m并且稳定后的水位降深曲线，同时采用式(8)计算得到水位降深曲线，均如图15所示，由图中可以看出，两者基本吻合，从而验证了理论方法的计算结果能较准确描述实际基坑外水位降深趋势。

图15 监测断面2-2处水位降深对比

5 结 论

(1)由基坑降水模型试验可知，在降水条件相同的情况下，由于绕渗作用的影响，基坑内降水有效影响深度大于基坑外，基坑内不完整井有效影响深度是基坑外的平均1.18倍；由于群井效应的影响，基坑内双井降水有效影响深度大于单井，基坑内双井同时降水有效影响深度是单井降水的平均1.12倍。

(2)基于巴布什金潜水层完整井和不完整井涌水量理论计算公式，结合潜水不完整井等效为潜水完整井思路，推导出不完整井降水有效影响深度理论计算公式。通过将理论计算结果与模型试验结果对比，得到理论计算公式更适用于基坑外不完整单井有效影响深度的计算，而运用于基坑内不完整单井和双井有效影响深度的计算时分别需乘以放大系数1.18和1.18×1.12。

(3)在地连墙深度范围内，基坑外土层中孔隙水压变化值随深度的增加而增大，基坑内不完整井降水引起基坑外地层内降水曲线为“先下凹再上凸”型，基于模型试验数据，通过曲线拟合得到基坑外降水曲线方程。

(4)以实际工程为例，数值模拟基坑内不完整井降水有效影响深度和基坑外水位降深曲线；同时采用本文推导的理论计算公式计算实际基坑内降水有效影响深度及降水引起的坑外水位变化；将理论计算结果与数值模拟结果进行对比，有效影响深度误差较小，降水曲线基本吻合，从而验证了理论计算公式的正确性和合理性。