基于光学引导下飞行员操纵着舰建模

张凯伦，韩 维，陈志刚

（海军航空大学，山东烟台264001）

飞行员驾驶飞机着舰是舰载机任务中非常重要的一环，由于着舰环境有大量不确定性因素可能导致意外事故发生[1]，故飞机着舰对于驾驶员而言是一项极具挑战性的任务[2]。

在飞机着舰过程中，对驾驶员的研究一般有[3]：驾驶员行为、舰载机动力学、FLOLS等几个方面，在驾驶员的操作行为上MuRuer等人研究单自由度补偿任务并提出MuRuer驾驶员模型，Ronald Hess提出基于跟踪任务的多回路的驾驶员模型[4-6]，70年代提出的最优控模型（OCM），假设飞行员经过严格的训练为该控制模型的基础。随着智能算法的普及开始将智能算法应用到驾驶员模型中[7]。在舰载机动力学方面，王立新[8]等建立在环境的随机干扰下的舰载机动力学模型，对着舰的安全性的研究做了仿真。在光学引导方面有杨一栋等人对FLOSL光学系统的仿真[9]。

驾驶员模型主要包含驾驶员的操纵行为模型以及驾驶员的视觉感官模型[10]。通过对驾驶员操纵模型以及驾驶员的感官模型进行改进，从而建立一个较为合适的驾驶员着舰的模型。以往的驾驶员的操纵模型中增益项都作为常值计算，而实际情况其增益项会随反馈的信号不同而产生差异[11]。对于驾驶员感官系统而言，之前的研究都将驾驶员输入都以数值的形式作为反馈，但真实情况飞行员是感知不到数值的差异，需要依靠灯光的信号大概了解下滑轨迹与设定好的轨迹的差距[12]。因此，根据这两点对驾驶员着舰模型作相应的改进。

本文基于上述两点的不足，从驾驶员操纵杆的增益与驾驶员的视觉感官两方面分别运用增益项的自适应改进以及驾驶员的视觉模糊化处理来解决上述的不足。

1 驾驶员跟踪模型

Ronald Hess提出关于着舰任务下的一个多回路的驾驶员模型，该模型的优点是有较少的限制条件，所以适合用于实际的进舰模型的研究。驾驶员任务跟踪模型如图1所示。

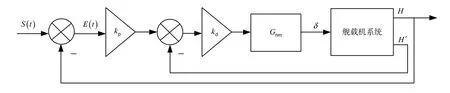
图1 驾驶员任务跟踪模型Fig.1 Pilot task tracking model

图1中：H为舰载机系统的高度输入指令；r为高度输出的速率变量；S为整个人机系统的输入量，kp和kd分别为偏差环节的以及的增益环节；Gnm表示驾驶员肢体的行为模型。

单轴的跟踪任务的驾驶员模型的控制率为：

2 驾驶员增益的改进

对于飞控系统的增益设计上，大部分都将其设置为常值，但是飞行员在操作飞机时，其增益项会随系统反馈的信息中会产生自适应调节的过程。下面对其增益项kp和kd自适应改进。

状态变量是完全可观察的，被控对象的状态方程为：

式（3）中：H和H'分别为高度输出和高度输出速率；Am和Bm为系数且大于0。

其参考模型的状态方程为：

式（4）中：Hm为模型输出；r为系统指令输入；Ap和Bp均为系数且大于0。

状态误差方程为：

由此可得：

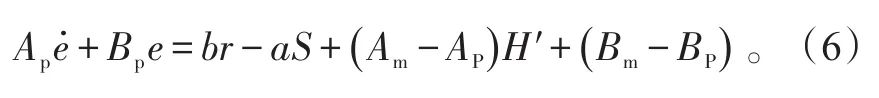
控制率δ可以表达为：

将式（7）代入（6）中可得：

对于人机的跟踪控制系统的任务，可利用Lyapunov稳定性理论来求得kp和kd的自适应率[11]，使其误差收敛。

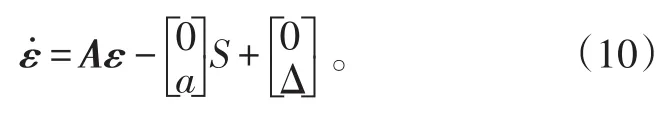
将式（1）代入式（8）可得：

为使方程左边趋于0，设计Lyapunov函数：

对式（12）求微分后得：

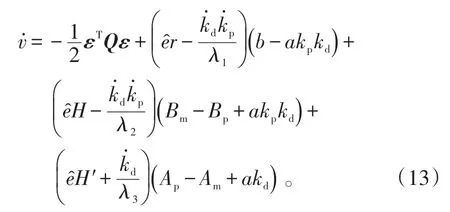
本文假设参考跟踪模型Hm和以及指令输入r都可设定为0，则其自适应率为：

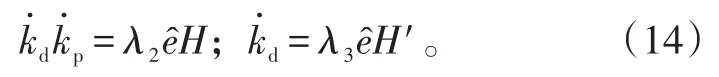
3 驾驶员视觉感受模型

3.1 光学助降系统的特点

当舰载机准备着舰时，在离航母的一段距离得到下滑的指令，飞行员开始人工操纵着舰。图2为飞机进舰图，飞行员控制飞机沿着所需的滑翔坡滑行，保持一条路径角度约为-3.5°的理想下滑轨道[12]。飞行员通过观察FLOLS光学助降系统获知飞机的下滑轨道与理想的下滑轨道的高度偏差，根据偏差的大小来操控飞机尽量向理想的下滑轨道靠拢，并最终在理想的位置完成着舰，并成功完成飞机阻拦任务[14]。

FLOLS向驾驶员提供高度偏差信息，主要影响纵向着舰过程，其主要组成部分是基准灯组和瞄准灯组。基准灯是一排水平固定的绿色灯组，向驾驶员显示理想下滑道的位置。瞄准灯组是一排竖直的灯组，由菲涅尔光学透镜组成，与理想下滑面平行并产生线性非常好的光束。这些光坡面在航母后方形成了垂向张角为1.5°的光学区域，每排灯提供0.3°的光源覆盖。在飞机着陆飞行期间，飞行员可查看可移动“球”在FLOLS景象中的位置。菲涅耳透镜的垂直光覆盖度将实际的飞机相对位置分成不同的相对位置范围，这些位置范围可以用图3中所示的“球”来标记当在理想下滑道观看“球”将与绿色基准灯对齐。当人类飞行员高于所需的下滑坡度时，“球”就会出现在基准灯上方。相反，当飞行员在预期的下滑坡度以下时，会看到低于基准灯的“球”。如果飞机的飞行位置离基准灯越来越远时，“球”的景象会呈现红色代表着舰危险。如果飞机偏离下滑道过远“球”将会从视野中消失。因此，人类驾驶员可以方便地估计高度误差。

图2 飞机进舰图Fig.2 Aircraft land carrier

图3 菲涅尔透镜示意图Fig.3 Fresnel lens

3.2 驾驶员视觉模糊建模

飞行员通过FLOLS系统感受高度误差的感测过程反映了模糊性。如图2中所示，飞行员感受“球”的位置时，认为是0.5倍球的高度，但实际可能是0.4倍的球的高度差。感测高度误差的过程基于人类飞行员的经验，受到飞行员主观性的影响。

基于模糊逻辑控制理论，模糊传感器块包括3个主要部分：模糊器，模糊推理和解模糊器[14-15]。模糊传感器输入和输出之间的关系取决于模糊推理以及基于飞行员的经验和知识的决策。然后，模糊器将FLOLS光学场景转换为飞行员所理解的高度偏差，解模糊器将模糊推理结果转换为以“球”测量的感测高度误差[16]。最后，几何关系模块将感测到的“球”中的高度误差转换为数值中感测到的高度误差。基于模糊逻辑控制理论，驾驶员感知过程变为数学运算[17]；飞行员传感器系统的模糊可以被量化和建模[18]。

表1为视觉感受的模糊高度偏差，图4为隶属函数。

表1 视觉感受的模糊高度偏差Tab.1 Fuzzy height deviation of visual perception

图4 隶属函数Fig.4 Membership function

由飞行员的视觉感受的偏差作为指令的输入，驾驶员的任务跟踪模型根据高度偏差的大小而实行不同的操纵策略。通过飞行员对菲涅尔透镜的光学引导信息的感知过程，并集成人机系统中各要素模型来建立光学助降系统引导下舰载机着舰人机系统的仿真模型，驾驶员根据实际高度的偏差对飞机进行操纵使飞机快速回到理想的下滑位置及姿态，见图5。

图5 人机系统Fig.5 Man-aircraft system

4 FLOLS引导下的着舰仿真

下面设置一个仿真算例来验证对文中建立的驾驶员操纵飞机着舰的模型的合理性。舰载机的进舰速度大约是69 m/s，下滑角是-3.5°，航母高度大约为30.6 m，吃水深度大约是10.7 m，舰载机的重心高度大约是2 m，所以舰载机大致的着舰高度为21.9 m，舰载机在距离舰载机水平位置约为1 511 m获得下滑道窗口，从开始着舰21.6 s左右时舰载机在指定的位置完成着舰。设定飞机的初始位置偏高12.2 m，约为2个“球”的高度，经过仿真获得着舰过程中飞机的状态变化以及舰载机下滑轨迹的变化如图6所示。

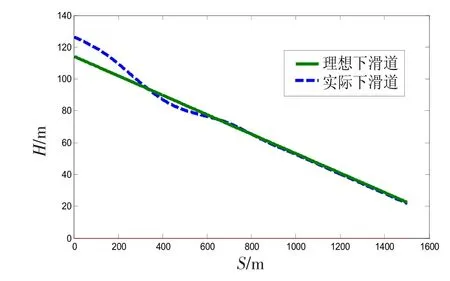
图6 飞机下滑轨迹与理想轨道对应图Fig.6 Flight glide path relative to carrier

从图6中可以看出，当飞机偏高约2个“球”的时候，驾驶员为使飞机能够在合理的时间内快速控制飞机使其接近原先预设的下滑轨迹上飞机所作出的位置和姿态的改变。当驾驶员看到飞机位置偏高时，首先压杆并让飞机低头使飞机能快速下滑使飞机快速修正高度的偏差。大约在8 s左右飞机的高度偏差已经基本修正，但是飞机的姿态还没有修正到理想状态，因此，飞机在高度修正、下滑角以及操纵杆都出现连续的波动。在大约15 s的时候，由于高度误差逐渐较小，飞机的姿态渐渐趋于稳定，从图7、8可以发现在15 s以后飞机的下滑角以及迎角都趋于平缓，飞机的实际下滑轨迹也基本与理想下滑道重合。根据图9可知，当飞机需要快速修正误差时，速度会有小幅度的上升，由于飞机速度的响应属于长周期变化，所以当飞机的姿态角趋于平稳时，速度依然持续变化中。

图7 飞机下滑角变化Fig.7 Flight path angle history

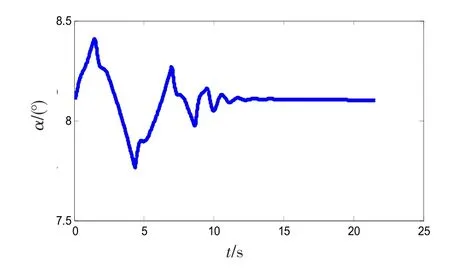
图8 飞机迎角变化Fig.8 Angle of attack history

图9 飞机速度变化Fig.9 Flight velocity history

5 结束语

本文改进了驾驶员的模型参数的设计方法，在驾驶员的视觉感知模型上利用模糊控制的理论进行改进，在菲涅尔透镜的引导下，能够使驾驶员在一定的高度偏差下准确跟踪预设好的下轨迹，并在指定位置顺利着舰。仿真实验的结果也表明，驾驶员进舰的结果和实际的飞机特性相接近，可以作为驾驶员操控着舰的参考。