基于时域分析法的无人机飞行质量综合评价方法

王玉伟，高 永

（海军航空大学，山东烟台264001）

数据表明，飞行器操控人员在复杂天气条件下决策失误，或操作不规范等是引起飞行事故和事故征候的一个重要原因[1]。飞行操作属于一种极为特殊的技能，飞行技术的获取、保持以及提升只能依赖于飞行训练这一种途径。同时，飞行训练也是确保飞行安全最为关键的基础。当前世界上，无论是有人机还是无人机，飞行训练的效能评估都已成为全世界飞行训练行业的难点之一，在整个训练支持技术研究领域，飞行训练质量分析评估技术已然变为研究热点。对于传统飞行训练质量管理办法，在飞行训练期间，数据的收集依赖于手工完成，人工主观地对飞行训练期间出现的问题、训练质量进行评估，这种分析评估方法效率低下，分析准确度不高，主观性强。

针对飞行训练质量评价，学者们开展了大量的研究工作，空军航空大学高文琦、钱鑫等人[2-6]建立了一套飞行训练成绩评估数学模型，这一系统对各个阶段评价指标进行了制定，对飞行成绩采用飞行参数误差进行评定，系统同时还具有维护数据、成绩统计等不同功能，整体性和操作性都很强，但是在各参数指标得分方法方面存在明显缺点。仅仅考虑了参数每单个采集点的范围决定单个点得分，再叠加求平均得出指标得分，并没有进一步分析数据总体的统计特征变化，如均值、标准差、偏度等等。这样评价方法不够细致，导致结果可信度不够。

为此，本文提出一种基于时域分析法的无人机飞行质量综合评价方法。

1 飞行质量综合评估结构层次

基于综合评估成绩是一个起落飞行架次的成绩，可以将评估模型自上而下分解成5个层次：飞行任务层、飞行阶段层、飞行科目层、飞行动作层、基本动作层。飞行任务层主要根据无人机作为平台担负的使命任务来划分，其对特定的飞行阶段及飞行品质有严格要求，需要在综合评估时加大权重，如执行光学侦查任务的无人机。为保证侦查信息的精确性、图片的清晰度，需要无人机有较好的巡航稳定性，在保持速度和高度的同时，还应有较好的抗干扰风能力。所以，进行综合评定的时候，必须加大无人机稳定性评价权重。相反，对执行突击任务的无人机，就需要有较好的机动性。因此，在综合评定时要增加机动飞行的评分权重。飞行阶段层是根据飞行航迹来划分，其对特定阶段的飞行安全和操控难易度有要求。如对飞行安全构成威胁的主要因素包括起飞和着陆等，尤其是舰载无人机。每个飞行阶段又存在多个飞行科目。每个飞行科目同时是由数个飞行动作进行编排所构成，这些动作主要包括筋斗类、盘旋类、升降转弯类以及其他不同战术动作，它们构成了飞行动作层。针对不同的飞行动作进行飞行质量评价往往不具备可比性，也无法用一套标准体系衡量所有的飞行动作。为了解决这一问题，需要将一个飞行科目分解成具有可比性、容易建立指标体系的基本飞行动作。可知任意一个复杂动作都可以分解成平飞、上升、下滑、转弯、横滚这5个基本动作，也称作基本动作层。图1为飞行质量综合评估结构层次。可以看出能否合理地评价出基本动作层是整个飞行质量综合评价的关键，得出基本动作评价，再根据具体飞行要求确定各个基本动作所占权重，即可求出飞行质量综合评价。

图1 飞行质量综合评估结构层次图Fig.1 Structure of the comprehensive assessment of flight

2 基本动作层评价指标体系

无人机飞控板所记录的数据众多，选取合适的评价指标是一个很重要的问题。有的指标虽然重要，但并不能起到实质性、决定性的作用。为确保评价指标体系的准确、实用以及科学性，在选择评价指标时遵循下述原则[7-10]。

1）系统性原则：对于评价指标体系，能够对被评价问题各个方面进行反映，实现对飞行质量全过程的反映。

2）科学性原则：评价指标体系元素构成、结构都能够对飞行质量真实情况进行反映，方法、内容都合理、科学。

3）可比性原则：对于评价对象必须能够对比、公平、可度量，不能存在明显倾向性。

4）实用性原则：评价指标可测量、可获取、操作简便实用。

参考上述指标选择原则，依据飞行大纲训练要求、资深的飞行员多年飞行经验，构建基本动作层评价指标体系，见表1。

表1 基本动作层评价指标体系Tab.1 Basic action evaluation index system

3 时域分析原理与指标选择

3.1 时域分析原理

时域分析法是指系统在输入一组变量时，以输出量的时域f(t)为基础，分析系统的瞬态和稳态特性。时域分析直接在时间域中对系统进行分析，它以时域抽样原理为基础，因而时域分析法直观易懂，分析方便。广泛应用于故障诊断、系统控制等领域[11-13]。

在本文的研究中，所有飞参数据均为Matlab数据的double类型，每组数据包括2列：一列为时间，另一列为记载的数据（速度、高度、GPS坐标等变量），即分析的时域输入量为时间，输出量为记载的数据。以时间为自变量描述，可以对记载信号进行滤波、放大、统计特征计算、相关性分析等处理。计算得到的时域参数的参数指标，一类是有量纲指标如峰值、均值、方差、歪度、峭度、均方根值等；另一类是无量纲指，即波形指标、脉冲指标、峭度指标、歪度指标和裕度指标等，这些参数指标反映了记载数据的性能，即反映了飞行训练数据的质量。

3.2 时域分析指标

为了分析方便，并立足于飞参数据现实需求，本文选择以下几类指标对数据进行分析。

3.2.1 均值分析

均值指一组数据或变量的平均值，也就是数据之和除以数据个数，均值一定程度反映了数据总体变化趋势和规律。飞参数据的均值反映了一段时间内飞行状态的稳定性与变化趋势，所以，选择将均值作为一个指标进行分析，均值计算表达式为：

3.2.2 方差（标准差）分析

方差是在概率论和统计中应用较多，它可以衡量一组数据的离散程度，表征一组随机变量与其数学期望之间的偏离程度的大小。

随机变量A，若存在，则称之为A的方差，记为称为随机变量A的标准差。

从方差定义可以看出，若变量X的取值集中在期望附近较小的一定范围，则方差较小；反之，若变量X取值偏离期望程度较大，则方差较大。

在研究飞行质量的过程中，研究飞行数据的方差即偏离程度，可以反映飞行员对操作状态的感知能力和调整能力，因而将方差作为评价指标之一。

3.2.3 偏度分析

偏度是用于衡量一组数据分布的不对称程度的指标。偏度指标α的数学表述是指该组数据三阶中心矩与标准差三次方的比值：

式（3）中：ν3代表3阶中心距；σ为标准差。

正态分布曲线左右完全对称，三阶中心距等于0，即α=0。当分布不对称时，见图2。当α=0时为正态分布；当α＞0时为正偏斜；当α＜0时为负偏斜。

图2 偏度偏斜示意图Fig.2 Schematic diagram of skewness

在研究飞行质量的过程中，研究飞行数据的偏度即不对称程度或偏斜程度，可以直观反映飞行的操作习惯，所以偏度也作为评价指标的一项。

3.2.4 峰度分析

峰度是衡量一组数据分布的集中程度的指标，峰度也可以量化分布曲线的尖峭程度，可以反映操纵灵敏程度，所以选择作为评价指标。

峰度指标β的计算式为：

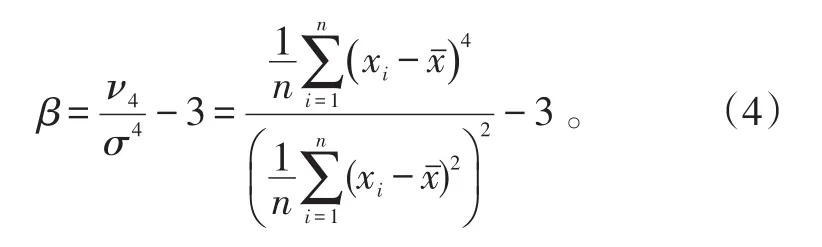
式（4）中：ν4是四阶样本中心距；σ是标准差；xi是第i个值；是样本平均值。

当峰度指标β＞0时，表示数据散布程度相对正态分布更加集中，表现在曲线上即曲线呈尖峰状态。

当峰度指标β=0时，分布为正态分布，表现在曲线上就是曲线呈正态曲线。

当峰度指标β＜0时，表示数据散布程度相对于正态分布更加分散，表现在曲线上就是曲线呈低峰状态。如图3所示。

图3 峰度状态示意图Fig.3 Schematic diagram of kurtosis

4 基本动作层评价数学模型的建立

4.1 指标权重方法的确定

在主观赋权方法当中，序关系分析法（G1法）计算量较于特征值法成倍的减少，方法简单直观，对元素或指标的个数没有限制，具有保序性，且相比于层次分析法，G1法无需矩阵一致性判断，计算过程非常容易[14-18]。因而本文采用G1法对飞行基本动作指标权重系数进行确定。

4.2 G1法原理及计算步骤

G1法是一种主观分析法，每一步调整都可以将专家的意愿进行体现，调整过程明确、方法简单。其优势显然不仅在于能够建立完全一致判断矩阵，而且对最终序列关系进行确定时无需构造判断矩阵[7]。求各个指标权重具体步骤如下。

4.2.1m位专家序关系一致时

1）确定指标间序关系。依照重要程度进行排序，最重在前，次重靠后，得到关系序列x1＞x2＞…＞xn。

2）xk-1和xk之间相对重要程度的对比判断：

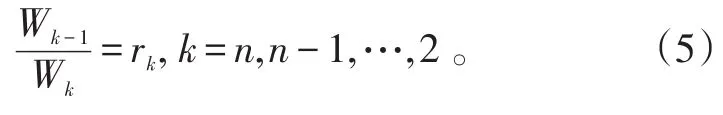
表2 rk赋值表Tab.2 Assignment table ofrk

3）指标权重系数计算。

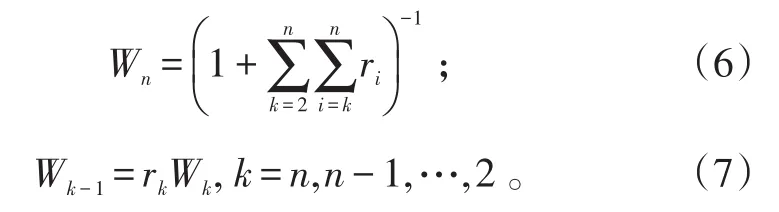
4.2.2m位专家序关系不一致时

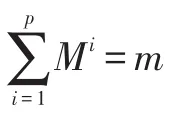
得到指标权重系数为：

4.3 时域指标及总指标得分方法

以基本动作层中平飞阶段为例建立评价模型。每个评价参数指标都有4个时域分析子指标，利用参数距离计算，得出第z个参数第i个时域分析指标的成绩为：

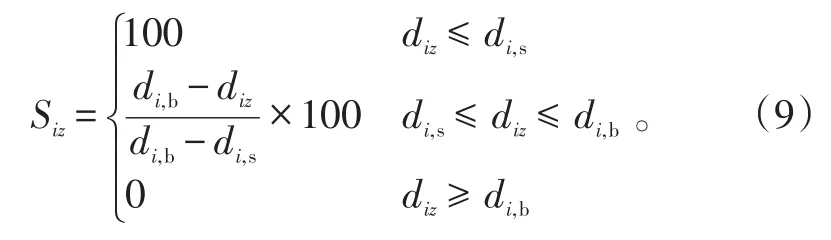
式（9）中：i=1,2,3,4,z=1,2,3,4,5；diz为第z个评价指标在第i个时域指标的实测结果与预定时域指标的误差；di,s为可忽略误差；di,b为允许存在的最大误差。

可以得到平飞第z个指标的总分为：

式（10）中，Wi为G1法求得的时域指标间的权重系数。

各参数指标权重系数Yz同理可得，即该阶段的平飞动作飞行总成绩S为：

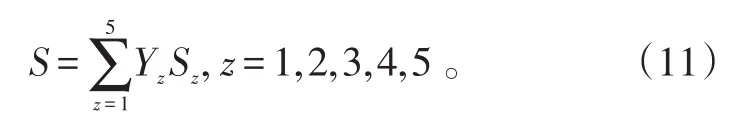
5 飞行质量评价实例

为验证评价模型的可行性，选择4名操控手作为评价对象，进行平飞任务，设定平飞任务计划：高度保持200 m，速度保持30 m/s，航向角保持0°，滚转角保持0°，俯仰角保持5°。设置各参数的时域分析指标可忽略距离di,s及允许存在的最大距离di,b。其中，平飞高度数据及其时域分析计算结果，在Matlab中实现效果如图4～7所示。其他参数的时域指标同理可得，具体得分如表3所示。

图4 均值计算Fig.4 Mean calculation

图5 标准差计算Fig.5 Standard deviation calculation

图6 偏度计算Fig.6 Calculation of skewness

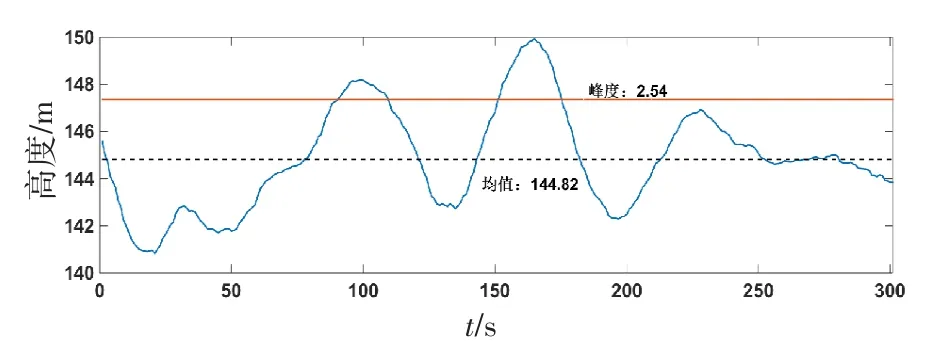
图7 峰度计算Fig.7 Kurtosis calculation

表3 某操控手平飞成绩得分Tab.3 Score of a control hand level flight

G1法计算得到的时域指标间权重向量为：

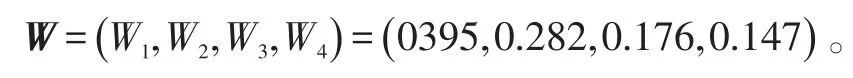
评价指标间权重向量为：

将W、Y代入式（10）、（11）得该学员平飞总成绩为82.085。

同理，其他学员的成绩分别可得：87.509、72.386、74.525。

教员传统打分方法依据飞行训练大纲，实行5分、4分、3分制，得出成绩分别为：4、4、3、3。

可以看出，传统打分方法得出的分数只有3分、4分或5分，区间太小，不能合理地区分学员的操纵水平高低。比如，前两位学员的成绩利用本文方法的得分是有差距的，而在传统方法下，2位学员的成绩却是一样的。而且传统方法依据飞行大纲不能对每个评价指标定量分析，不少指标只是定性分析，质量评价存在主观性。传统方法评价只对指标定了范围阈值，缺少对每个参数数据时域分析。比如，传统方法规定高度误差在20 m以内，高度得分为满分5分。如果以此方法打分，一个高度在标准高度20 m范围内来回波动和一个高度稳定在标准高度不变的成绩得分是一样的，明显传统方法评价结果不细致，说服力不足。

本文提出的飞行质量评价模型对所有指标进行定量分析，并利用时域分析原理，结合飞参数据现实需求得出了合适的时域分析指标，指标信息能充分反映各参数中学员的操纵水平，质量评价结果更合理。

6 结束语

本文针对部队无人机飞行训练质量评估方法评价不细致、效率低、主观性强的问题，提出了一种基于时域分析法的无人机飞行质量综合评价方法。实例显示，这一模型能够纠正传统评价方法评价不细致、主观性强等现象。利用时域分析原理，结合飞参数据现实需求得出了合适的时域分析指标，并用G1法确定指标间权重系数，评价结果公正客观，便于对训练期间的问题进行查找，提升飞行员操作水平。

下一步根据具体的飞行任务要求，由基本动作层为基础，调研确定每个层次中子层次的评分标准，根据建立的飞行质量综合评价数学模型编写成相应的软件，将需要进行评价的飞行数据输入进去，即可自动获得飞行质量评价结果。