耦合调和振子网络系统的联合连通同步*
张华 万明非 颜青 杨伟
(1.重庆理工大学 理学院, 重庆 400054) (2.铜仁学院 大数据学院, 铜仁 554300)
引言
网络型调和振子系统来源于由阻尼、 弹簧和质量构成的一种耦合力学模型.二阶网络型调和振子模型如下所示[1]:
(1)

(2)
其中ui(t)=-aij(vi(t)-vj(t)),i=1,2,…,N,表示对对第i个振子的控制输入.Ballard等对模型(2)进行了离散模化处理,并提出了一个离散时间下的控制输入协议[2].Su等利用振子间感应距离的概念,通过建立适当的控制输入使得每个振子在没有任何连通假设下仍能达到同步[3].Zhang等利用平均速度的概念在无法测量速度的情况下用位移耦合代替速度耦合分析了调和振子系统的同步[4].
在现实世界复杂的网络环境中,系统的网络结构不可能一直都保持不变,并且不是所有的系统都是同构系统.此外,外界各种因素对系统的干扰可能造成诸如通信阻隔、通信延迟、控制输入缺失、参数扰动以及传输误差等多方面的问题.为此,孙一杰等分析了异构多智能体在有向图下的广义平均一致性,利用非负矩阵理论和特征值扰动等方法,提出了一种基于辅助变量的线性一致性协议使得系统能在任意强连通有向结构下达到一致[5].Zhang等利用采样控制技术研究了耦合调和振子系统具有控制输入缺失的情况,通过建立误差系统求出系统的迭代解,然后通过分析迭代矩阵的范数得到了系统一致的充分条件[6].Zhou等利用脉冲控制技术分析了二阶调和振子系统的脉冲一致性,通过建立相应的误差系统,利用矩阵谱分析的方法得到了系统的稳定所需要满足的充分条件[7].Zhou在文献[6]的基础上分析了具有输入时滞的网络型调和振子系统的采样同步问题[8].Sun等在不考虑控制输入缺失的情况下将文献[6]中的无向图推广到有向图情形,并分析了时滞对系统同步性能的影响[9].此外,Sun等还分析了具有随机扰动的阻尼器的调和振子系统[10],通过建立随机李雅普诺夫方程来得到系统稳定的充分条件.Wang基于脉冲控制技术,在振子耦合瞬间加入了测量误差,利用均方收敛的概念得到了系统同步的充分条件,并给出了系统的收敛域[11].
值得注意的是以上研究都是基于系统拓扑结构图是连通的(拓扑结构为无向图)或是有一棵有向生成树(拓扑结构为有向图)的假设条件下讨论的.然而,在实际应用中由于各种外界因素的影响,系统的拓扑结构无法固定不变,并且每一时刻都能保持网络连通的条件也十分苛刻.所以在网络结构为切换拓扑或联合连通的情况下分析系统的同步性是有科学意义的.例如,唐朝君分析了切换拓扑下离散时间多智能体系统的包含控制[12].Hong等分析了二阶多智能体系统在联合连通下的引导跟随同步问题[13].Lin等在没有引导者的情况下分析了二阶多智能体的同步问题,并考虑了时间延迟对系统的影响[14].Mo等分析了异构的多智能体系统在联合连通下的引导跟随同步[15].Yu和Mu在自适应控制的情况下考虑了多智能体系统在联合连通下的引导跟随同步[16,17]. Wang在具有层次结构的系统中分析了联合连通下的引导跟随同步[18].然而,迄今就作者所知鲜有关于网络型调和振子系统在联合连通下的同步问题的研究报道.为此,我们在本文中分析了网络型调和振子在联合连通下的引导跟随同步动力学.
1 预备知识
1.1 符号说明

1.2 代数图论
令G=(ν,ε,A)表示一个图,ν={1,2,…,N} 代表图的顶点集,ε⊆ν×ν是图的边集.如果对i≠j,(i,j)∈ε都有(j,i)∈ε,则图G称为无向图,反之为有向图.矩阵A=[aij]N×N表示图的邻接矩阵,其中aij>0当且仅当(i,j)∈ε.称一个由图中边构成的序列(i,i1),(i1,i2),…,(il,j) 为点i到j的一条路径.如果图中任意两个不同的节点之间至少存在一条路径则称该图为连通图.
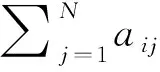
2联合连通下耦合调和振子网络系统的引导-跟随同步
令r0(t),v0(t)分别表示引导者的位置和速度,其动力学方程如下:
(3)
下面对系统(2)考虑如下控制输入协议:
(4)
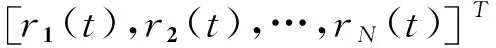
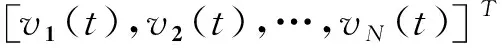
则系统(2)可以写成如下微分方程组形式:
(5)

假设1存在一个非空有界且有限的互不相交的连续时间序列[tk,tk+1),k=0,1,…,t0=0,对某一特定常数T>0,有tk+1-tk≤T.对每个区间[tk,tk+1),都存在一个互不相交的子区间列[tk0,tk1),[tk1,tk2),…,[tkj-1,tkj),tk0=tk,tkj=tk+1满足tki-tki-1≥τ,i=1,2,…,j,在每个[tki-1,tki)子区间上系统拓扑结构不变,只在在tki时刻改变.即切换信号σ满足当t∈[tki-1,tki),存在p∈p,使得
σ(t)≡p且σ(tki)≠σ(tki-1).
假设2在每一个区间[tk,tk+1)上系统所有可能的拓扑结构是联合连通的.




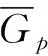
定理1带有引导者的调和振子系统在控制输入(4)下能够达到同步,如果假设1和假设2成立.
证明令误差函数e(t)=r(t)-r0(t)1N,s(t)=v(t)-v0(t)1N,x(t)=[eT(t),sT(t)]T,则:
(6)
记:
(7)
根据同步的定义,系统(5)同步等价于系统(6)的零解是渐近稳定的.
构造如下Lyapunov函数:
V(x(t))=xT(t)Qx(t)
(8)
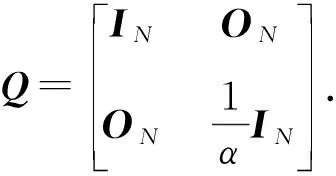
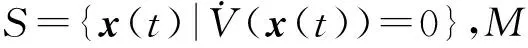
Hσ(tk1)+Hσ(tk2)+…+Hσ(tkj)>0
如果:
则有:
sT(Hσ(tk1)+Hσ(tk2)+…+Hσ(tkj))s=0,
即:
Hσ(t)s(t)=0,t∈[tk,tk+1).
下面证明M中只有(6)的零解. 由于M为系统(6)的不变集,即M中的元素为(6)的解,且M⊂S,则∀x(t)∈M,有:
该系统通解为:
(9)
由Hσ(tk1)+Hσ(tk2)+…+Hσ(tkj)的正定性,要使sT(Hσ(tk1)+Hσ(tk2)+…+Hσ(tkj))s=0恒成立,需s(t)≡0.所以要使x(t)∈M,需有s(0)=0.
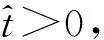
不妨设e(0)≠0,那么存在一个1≤q≤N使得eq(0)=c≠0,那么方程(7)的第q个系统有如下解:
(10)

3 数值模拟

引导者初值r0(0)=1,v0(0)=1.系统在这3种切换方式下随机切换情况下,系统的位移和速度状态的时间历程仿真结果如图2、图3所示.
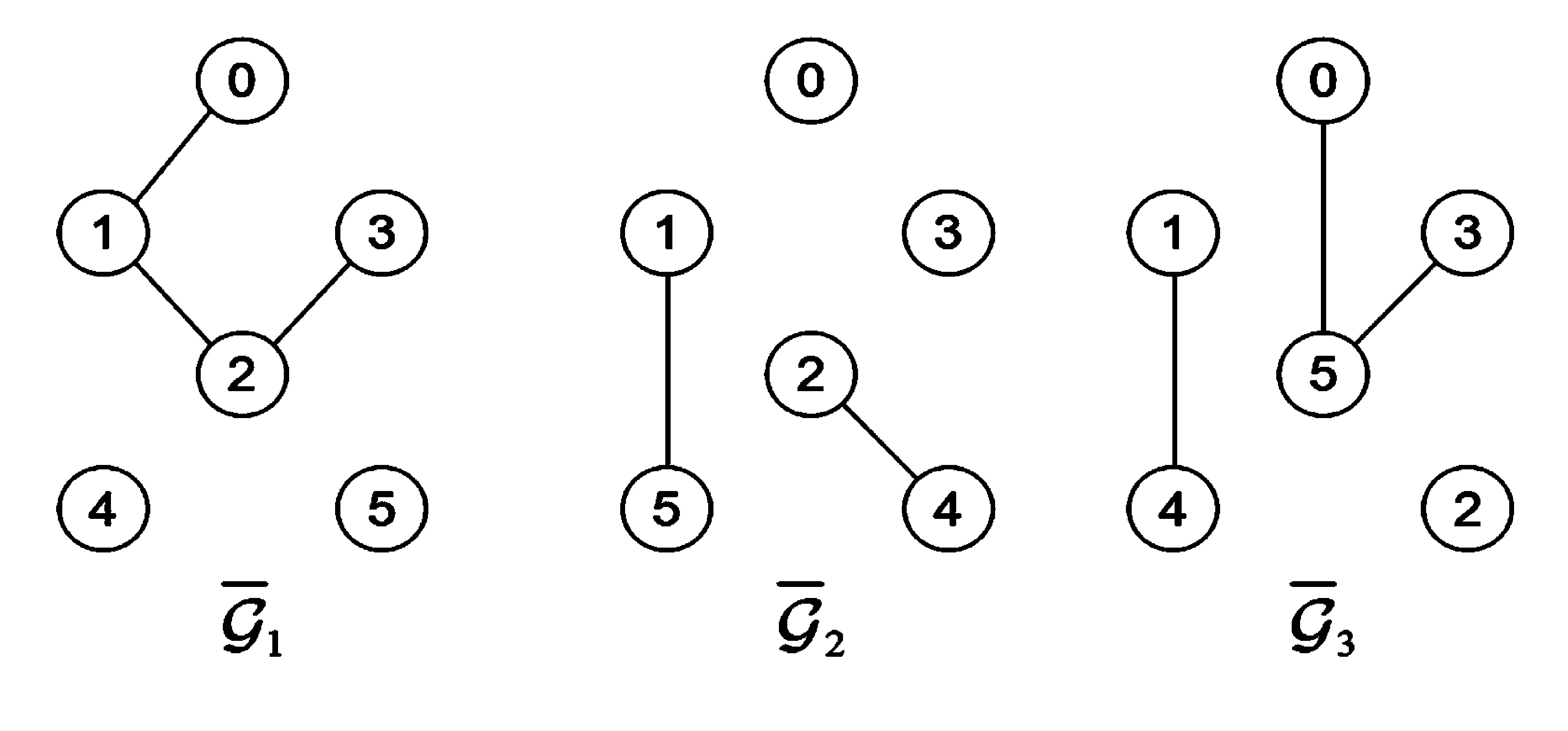
图1 三个联合连通网络拓扑结构Fig.1 Three jointly-connected network topologies
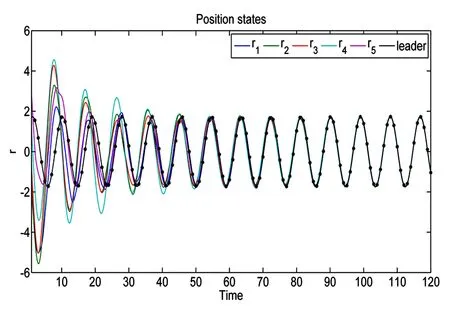
图2 引导者-跟随者的位移状态时间历程曲线图,*表示切换时刻引导者的位置Fig.2 Time response of the position states of the leader-follower system,where the asterisks * show the position states of the leader at the switching instants

图3 引导者-跟随者的速度状态的时间历程曲线,*表示切换时刻引导者的速度状态Fig.3 Time response of the velocity states of the leader-follower system,where the asterisks * show the velocity states of the leader at the switching instants
4 结论
本文在系统通信拓扑结构具有联合连通特性这一假设条件下,分析了网络型调和振子系统的引导-跟随同步问题,在无向网络拓扑结构下证明了所有的跟随者状态最终与引导者保持一致.数值模拟也进一步验证了理论结果的正确性.对于没有引导者的网络系统,其同步轨道与拓扑结构的切换方式有关系,其准确解析表达式目前我们还没有一个确切的算法能够算出,希望在后续研究中给出相关结果.

