基于阻抗法的多螺栓连接预紧扭矩检测试验研究*

任凯 张子涵 杜飞 吴冠男 徐超

(西北工业大学 航天学院, 西安 710072)

引言

随着微小卫星技术迅速发展,缩短发射准备时间的需求已经成了最直接的问题[1],而这就需要我们能快速及时地检测结构健康状况.卫星结构一般通过大量的螺栓连接的方式组装成为整体.由于装配过程中的操作不当、发射和再入过程中的动态激励等不可控原因,螺栓连接可能出现预紧力下降、连接界面错动甚至松脱等损伤现象,从而严重威胁航天器的结构完整性和系统功能性,所以监测螺栓连接松动就成了目前面对的主要问题.另一方面,空天飞行器逐渐成为各国关注的重点,而空天飞行器用于保持良好的气动外形和热防护的蒙皮与骨架的常见连接方式也是螺栓连接,为了能重复利用,也迫切需要针对螺栓连接预紧扭矩进行监测.

目前,机电阻抗[2]和超声导波方法[3]被广泛应用于航空航天结构健康监测.导波具有在结构中传播距离远,只需很少的传感器就可以实现对结构大范围地监测的优点,但当结构几何形状复杂、界面众多,即使在简单激励下,导波的频散、多模态特性导致其信号异常复杂,在多螺栓连接的结构中,提取出表征连接状态变化的特征信息将变得十分困难.

结构机械阻抗对于损伤较为敏感,利用压电传感器可以检测机械阻抗的变化,该方法对外界环境影响免疫力强,不依赖模型分析,故适宜复杂结构,适宜在线监测等优点[4].Liang等[5-8]最早提出了智能结构的阻抗分析方法,在阻抗分析的工作中做了大量的相关工作,他的研究奠定了基于压电陶瓷PZT的阻抗分析法的基础,其提出了PZT耦合结构的一维单自由度弹簧-质量-阻尼系统(SMD)模型的耦合电导纳表达式,分析了结构机械阻抗的变化对压电片电导纳的影响,以悬臂梁为例进行了实验验证.Sun等[9]利用压电传感器,对组合桁架进行了结构健康监测实验,通过对比损伤前后压电片电导纳的变化,验证了机电阻抗技术能准确识别出组合桁架发生的损伤.Bhalla等[10]研究了PZT在钢结构的初始损伤诊断中的应用,通过实验验证了机电阻抗法能有效地检测到钢结构的初始损伤.Yabin Liang等[11]利用PZT对销连接结构的载荷进行监测,结果表明阻抗实部对结构变化更加敏感.熊先锋等[12]对螺栓连接的四角固定铝板的螺栓松动状况进行了研究,证明了通过分析PZT阻抗的变化来检测螺栓松动状况的可行性.

目前学者针对基于机电阻抗的多螺栓的预紧扭矩检测方法的研究还不够深入,为此本文采用具有质轻,高效,制造容易,抗压等优点的压电陶瓷纤维复合材料MFC代替传统的PZT进行研究[13,14].针对常见的多螺栓连接结构,本文以两螺栓搭接梁为研究对象,提出了基于压电陶瓷纤维复合材料MFC的螺栓预紧扭矩检测方法.

1 基于机电阻抗的结构损伤识别原理

压电陶瓷材料是一种能够实现机械能和电能相互转换的功能材料,传统的PZT具有脆性大,密度高,硬度高,不易变形等缺点,使这类材料在应用上受到了很大限制,由NASA的Langley研究中心发明的压电陶瓷纤维复合材料MFC则具有优异的强度和灵活性.MFC是由矩形的压电陶瓷纤维夹在胶粘剂、电极和聚酰亚胺薄膜之间复合而成,电极和薄膜以相互交叉的方式接触,这样可以将电压直接传到压电陶瓷纤维上,或者由其传出.MFC作为一种智能材料,具有正、逆压电效应.当MFC在沿一定方向上受到外力的作用而变形时,其内部会产生极化现象,同时在它的两个相对表面上出现正负相反的电荷.当外力去掉后,它又会恢复到不带电的状态,这种现象称为正压电效应.当作用力的方向改变时,电荷的极性也随之改变.相反,当在MFC的极化方向上施加电场,MFC也会发生变形,电场去掉后,MFC的变形随之消失,这种现象称为逆压电效应.

借鉴基于压电陶瓷PZT与结构的相互作用模型[15],MFC与结构的相互作用可以用如图1所示的一维阻抗模型描述,MFC被看作为一个狭长的杆件,在交变电场作用下做x向的轴向振动,MFC一端固定,另一端与简化为单自由度系统的基体结构相连.

此时,粘贴在结构表面的MFC受到垂直于x方向的电场作用,该系统中MFC的电导纳为：

(1)

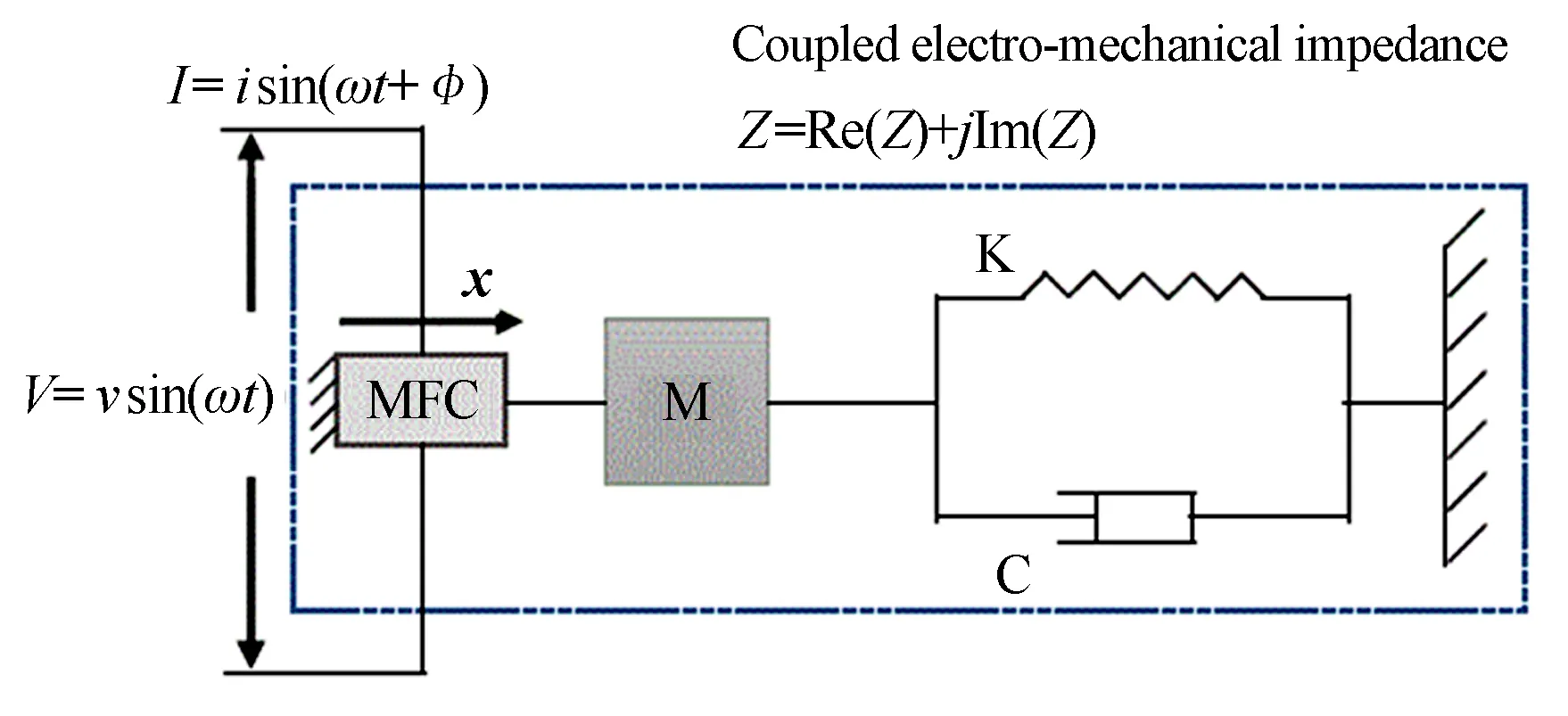
图1 MFC与梁结构机电耦合作用的一维模型Fig.1 1-DOF model of electromechanical coupling between MFC and beam structures

从方程(1)中可以看出,当压电材料的参数和性能保持恒定,与之相贴合的结构机械阻抗唯一的确定了MFC的电导纳.MFC的电导纳的任何变化都反映了结构的机械阻抗的变化,反映了结构中缺陷、损伤或其他物理变化.

相比于MFC的导纳模值、阻抗模值、阻抗虚部等参数,结构变化引起MFC的阻抗实部R=Re(1/Y)变化更为明显.因此,为了对螺栓的松动状况进行定性和定量的评价,本文以螺栓松动前后两组阻抗实部数据的均方根偏差RMSD作为指标：

(2)

2 实验研究

2.1 实验装置与试件

本文以图2所示的双螺栓搭接梁为研究对象.两端自由,两根相同的梁用两个M6螺栓相连,梁的几何尺寸为：ls=400mm,bs=60mm,hs=2mm,梁的材料为2024-T3铝,螺栓对称安装,相距32mm,距梁安装螺栓一端边界20mm,MFC型号为2814-p1,因为机电阻抗法敏感范围限于压电片附近区域[13,14],所以MFC应贴于螺栓附近,MFC中心距梁上下边界均为30mm,距有螺栓连接一侧边界50mm.阻抗分析仪型号为IM3570精密阻抗分析仪,选取MFC阻抗值的实部为测量对象.

图2 双螺栓搭接梁模型Fig.2 Model of double bolt lap beam

2.2 实验方法

因为基于机电耦合特性的机电阻抗技术工作频率高(30～500kHz)[4],所以先选取扫频范围为30～200kHz.查得强度等级8.8的M6螺栓标准扭矩为9～12N·m,由于所用铝板较薄,为防止铝板屈曲变形,取标准扭矩为6N·m,实验考虑了4种工况,分别是：工况1.两个螺栓扭矩均为6N·m；工况2.螺栓1扭矩3N·m,螺栓2扭矩6N·m；工况3.螺栓1扭矩3N·m,螺栓2扭矩3N·m；工况4.将螺栓1取下,螺栓2扭矩3N·m.

用扭矩扳手改变作用在螺栓上的扭矩,寻找阻抗实部的谱曲线上峰值频率与峰值大小的变化程度大的频段,作为敏感频段.通过计算此频段内损伤工况与标准工况(工况1)间的均方根偏差RMSD来判断螺栓松动状况.

2.3 实验结果

图3为四种工况中阻抗实部随频率变化的曲线,可以发现在40～43kHz,50～53kHz,72～75kHz,150.5～153.5kHz,164～167kHz,193.5～196.5kHz六个频段内,阻抗实部谱曲线上峰值频率和峰值大小变化比较明显,因此初步选择上述六个频段为敏感频段,得到工况2,3,4相对于工况1的RMSD如图4所示.从图中可以看出,40～43kHz和150.5～153.5kHz两个频段不能区分工况2和工况3,因此,以50～53kHz,72～75kHz, 164～167kHz和193.5～196.5kHz为敏感频段.

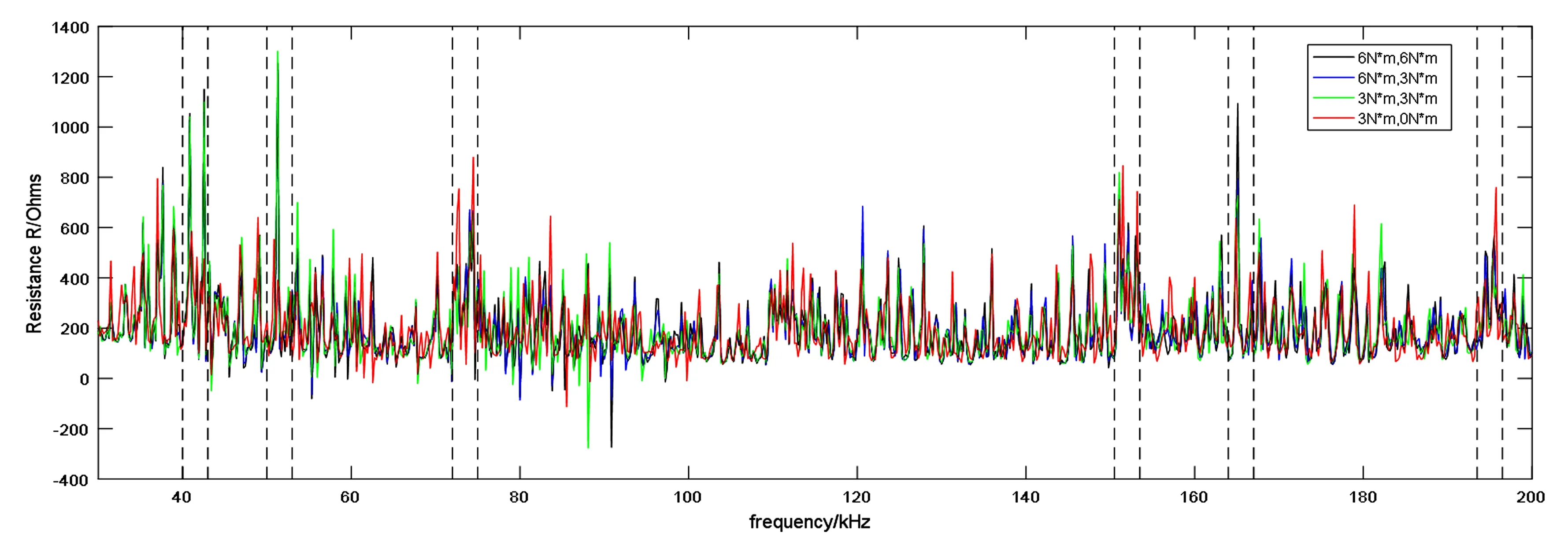
图3 不同扭矩水平的阻抗实部谱曲线Fig.3 Impedance real spectral curve under different torque levels

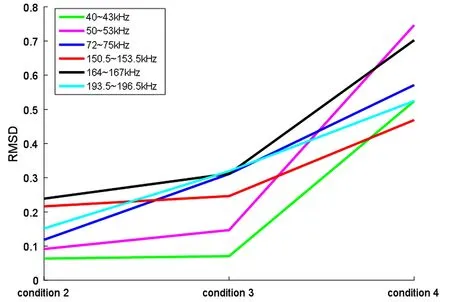
图4 其余工况阻抗实部数据相对于工况1的数据的RMSDFig.4 RMSD of impedance real spectral data under other operating conditions compared with that of the condition 1

在每个频段内,每组工况重复实验5次,以工况1重复实验5次得到阻抗实部数据的平均值为参考数据,计算各工况在对应频段相对于参考数据的RMSD,结果如图5所示.

从图5可直观地看出,同一工况下5组数据的RMSD波动较小,说明阻抗方法用于检测螺栓连接的搭接梁中螺栓松动实验有良好的可重复性.随着螺栓逐渐变松,螺栓上的扭矩下降,MFC测得的阻抗实部值与参考数据的RMSD逐渐增大,但变化较小.当有螺栓脱落后,MFC测得的阻抗实部值与参考数据的RMSD明显增大.

图5 各敏感频段内不同工况的RMSD(a)50～53 kHz; (b)72～75kHz; (c)164～167kHz; (d)193.5～196.5kHzFig.5 RMSD under different operating conditions in each sensitive frequency bands (a)50～53kHz; (b)72～75kHz; (c)164～167kHz; (d)193.5～196.5kHz

2.4 螺栓松动检测步骤

计算得到每组工况5次实验的RMSD的均值μ和标准差σ.建立包含参考数据和已知4种工况RMSD的均值和标准差的数据库.

步骤一、计算未知工况的RMSD.

步骤二、对比未知工况的RMSD与4种工况RMSD的均值和标准差.

假设在给定频段内,每种工况的RMSD服从正态分布,由未松动工况得到的RMSD落入工况1的(μ-2σ,μ+2σ)内的概率为95.44%,则由未知工况得到的RMSD若落入工况1的(μ-2σ,μ+2σ)内,未知工况即为未松动工况.若未知工况得到的RMSD不在工况1的(μ-2σ,μ+2σ)内,说明螺栓发生了松动,对比工况2,3,4的RMSD,就能判断出螺栓的松动程度.

表1 4种工况的统计值Table 1 Statistics of 4 operating conditions

为验证阻抗法能检测出螺栓上是否松动,对两个螺栓都施加扭矩3N·m,在4个敏感频段内计算其阻抗实部数据相对于参考数据的RMSD,如表2所示：

表2 未知工况的RMSDTable 2 RMSD under unknown operating condition

可以看出,在4个敏感频段内,未知工况的RMSD均未落入工况1的(μ-2σ,μ+2σ)内,且接近工况3的均值,说明未知工况螺栓发生松动,且松动状况与工况3接近.因此根据损伤指标RMSD,可以实现两螺栓不同松动工况的检测.

3 结论

针对工程中常见的多螺栓连接结构,本文以两个螺栓连接的搭接梁为研究对象,测量结构与压电陶瓷纤维复合材料耦合系统的阻抗实部,以敏感频段内阻抗实部的均方根偏差RMSD为损伤指标进行预紧扭矩检测.实验结果表明：

(1)敏感频段内阻抗实部的RMSD能够作为有效表征螺栓松动的损伤指标；

(2)根据实验建立了不同螺栓拧紧力矩下的阻抗实部均方根偏差数据库,并提出了螺栓松动检测方法.

(3)利用上述方法实现了对螺栓连接梁中不同螺栓预紧扭矩工况的检测.