主制造商供应商协同合作最优定价决策博弈与混沌分析*
王玥 陈洪转
(南京航空航天大学 经济与管理学院, 南京 211106)
引言
随着信息技术的飞速发展,复杂产品制造企业呈现全球化趋势.激烈的竞争、制造难度的增加、交货期的缩短等问题使得主制造商逐渐将有限资源集中在核心业务,以增强核心业务的竞争力,同时将非核心业务外包给供应商,与供应商建立协同合作的关系,由此形成了“主制造商-供应商”模式.目前,“主制造商-供应商”多利益主体的协同合作逐渐成为复杂产品研制与生产的主流生产模式[1],在国际航空工业界广泛采用,波音、空客等知名飞机制造商也运用这种模式.与传统的合作模式相比,该合作模式更加注重企业间的长期战略合作.在这种模式下,主制造商处于核心地位,协调各个节点的活动,供应商利用主制造商的技术和资源,参与到相关产品的生产项目中.由此,主制造商与供应商共享信息、共担风险,双方形成长期稳定的合作共生关系.为了达成价格、成本、利益等信息的协调,主制造商与供应商会进行多方面博弈,以便建立长期互惠互利的关系.价格作为影响销售的关键因素,在市场竞争中起着非常关键的作用,合理的定价策略可以使得供应链系统各方获得良好的利益,占领市场,因此主制造商与供应商十分重视价格的制定.
为了实现长期的合作,优化资源配置,主制造商与供应商之间对价格决策与利益分配会进行多次博弈.市场环境的多变与供应链中企业间的复杂关系,使得企业在进行价格调整时,可能出现决策失误的现象,继而影响平衡点的稳定性,令整个供应链的演化更加复杂,难以预测,甚至出现分叉与混沌现象.自混沌理论提出以来,其研究取得了丰富的成果[2],将混沌理论应用于供应链分析企业问题是国内外学者的研究热点.Agiza等[3]考虑有限理性的因素,对双寡头博弈过程建模,并分析其稳定性,发现分岔、混沌等复杂的动力学现象.Hwarng HB等[4]分析了多级供应链产生混沌的原因,提出了消除或减轻系统混沌的方法.Ma等[5]研究了以价格为决策变量的两家企业的动态竞争问题,并引入混沌控制策略使系统恢复有序的状态.Wei等[6]发现需求依赖库存的供应链系统会产生周期性波动现象,容易进入混沌状态.卢亚丽[7]基于有限理性策略与适应性策略,构建两寡头企业主从型Bertrand价格博弈模型,并研究该模型的动力学性质.董文波等[8]基于有限理性构建了具有溢出效应的双寡头价格博弈模型,探讨了价格调整率、产品同质化程度、知识溢出效应等相关参数变动对模型演化的影响.马军海等[9]基于四寡头垄断市场建立了市场的动态博弈模型,并应用复杂系统理论分析研究了系统的稳定性.龙剑军[10]基于集群企业的有限理性,采用两种不同的价格调整机制Navie和GD,在企业集群中构建起具集群溢出的双寡头Bertrand竞争博弈模型,分析了集群溢出对离散动态系统下价格均衡的影响,并进行了数值模拟.
此外,由于主制造商与供应商在系统中地位、势力、角色等方面的差异,主制造商作为核心企业主导着整个供应链,保持系统的稳定及竞争力,实现协同共生.为了约束企业间的行为,促使供应链资源得到良好配置,增强企业的收益,一些学者研究供应链采用协同机制等方法解决供应链的利益分配问题,使得企业共担风险,促进企业的长期合作.Mou[11]研究了非对称信息下,供应商采用数量折扣策略对于供应链绩效的影响,并验证了该策略的有效性.Cachon[12]分析了数量折扣、批发价格、双重收费策略下的供应链协同问题.Yao等[13]研究了回购策略下,价格敏感系数对于供应链系统的影响情况.Bo VDR等[14]构建了收益共享策略,在该策略下,供应链中企业愿意降低价格以提升供应链利润.Ma等[15]研究了一个制造商和两个零售商的供应链模型,证明了收益共享机制有效提高零售商的利润,稳定市场环境.Panda等[16]分析了一个三级供应链的协调问题,并提出合同谈判过程来解决利益分配问题.
现有文献主要针对传统供应链的协同制造模式,供应链的价格博弈与混沌的研究也多集中于寡头企业,缺乏针对复杂产品“主制造商-供应商”特点下价格的变动对于系统的影响.此外,有研究表明,供应链中成员间的合作关系都可以视为共生关系[17].供应链管理和运作的不同阶段对应着共生关系的若干阶段,系统外部环境构成了共生环境.因此本文主要研究一个主制造商和两个供应商的价格竞争博弈问题,为了实现双方长期稳定的共同发展,构建一个共生利润分配模型,供应商通过价格的下降实现市场的平衡,主制造商根据供应商价格的调整程度主动对供应商的受损的利益进行赔偿.通过这种稳定的经济合作共生关系,主制造商和供应商实现长期稳定的战略合作伙伴关系.通过数值仿真,分析了供应商间的价格调整速度对于系统稳定性的影响.研究了主制造商和供应商在共生利益分配模式下,共生利益分配系数对双方利益的影响.由此找到了系统的最优定价决策.结果表明,主制造商和供应商在建立共生关系后,利益相比于共生前均有所提升,系统的稳定区域也明显增大,市场更加趋于稳定.
1 模型与基本假设
考虑一个两级供应链,由一个主制造商和两个供应商构成.该供应链上企业协同研制产品,实现产品的开发与生产,假设主制造商与供应商均为独立的决策者,交易中主制造商供应商各自报价,其目的在于追求利润最大化.模型中的变量如下:
Pi(i=1,2)表示两个供应商各自产品的价格;
Ci(i=1,2)表示两个供应商各自的经营成本;
di(i=1,2)表示两个供应商出售产品各自的变动成本系数;
Ri(i=1,2)表示两个供应商各自的利益;
ki(i=1,2)表示两个供应商各自的价格调整速度;
w表示主制造商售出产成品分解到供应商提供产品的价格;
p表示主制造商售出产成品分解到供应商提供产品的成本;
Rm表示主制造商的利润.
根据模型的需要,做出如下假设:
假设1:根据经济学中需求函数的特点,考虑市场因素,假定其他条件不变,两个供应商提供差异化产品,供应商1的产品价格影响供应商2的产品价格,但是供应商2的产品价格不会影响供应商1的产品价格,即供应商1和供应商2的产品需求函数分别满足Q1=a1-b1P1和Q2=a2-b2P2-θP1.
假设2:两个供应商均以利润最大化为追求目标,进行下期决策时均采用有限理性决策[18].
假设3:两个供应商与主制造商协同合作价格决策,两个供应商降低产品价格,主制造商获得更多的利润,供应商按照一定比例分享主制造商的销售利润,实现合作共生,βi(i=1,2)表示供应商i的共生利益分配系数,即主制造商根据所得分配给供应商的比例.
2 模型构建
2.1 基本模型
在基本模型中,主制造商和两个供应商的利益函数满足如下关系式:
(1)
两个供应商均追求利益最大化,满足一阶条件为零,对两个供应商的利益求偏导,可以得到两个供应商的边际利益,即:
(2)
由此得到:
两个供应商根据有限理性策略,基于上期价格竞争的边际利益情况,对下期价格做出调整,则两个供应商的产品定价策略可表示为:
(3)
因此两个供应商的价格动态调整方程为:
(4)
2.2 共生利益分配模型
为了实现整个供应链的绩效水平的提升,主制造商基于一定的市场价格,通过供应商产品价格的降低来实现自身利益的增长.供应商价格的下降使得其利益减少,主制造商通过一定的利益共生机制补偿供应商缺失的利益,实现主制造商和供应商利益均增加的结果.则主制造商和两个供应商的利益函数变为如下关系式:
(5)
此时两个供应商的边际利益函数为:
(6)
同样的,可得:
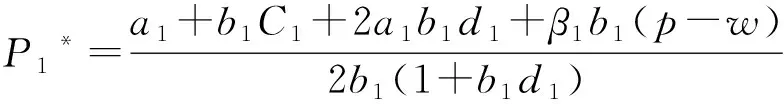
此时两个供应商的价格动态调整方程为:
(7)
3 数值模拟
3.1 基本模型
研究表明,非线性演化方程一般不存在解析解[7],因此为分析价格调整速度和共生系数对于系统和整个供应链的影响,并得出最优定价决策方案,假设a1=5,b1=2,a2=8,b2=1.4,C1=1.1,d1=0.3,C2=1.5,d2=0.1,θ=2.1,w=20,p=10,β1=0.2,β2=0.3,令两个供应商的初始价格为P1(0)=0.1,P2(0)=0.1,供应商二的价格调整速度为k2=0.1,随着供应商一的价格调整速度的变化,两个供应商的价格变动情况如图1所示.
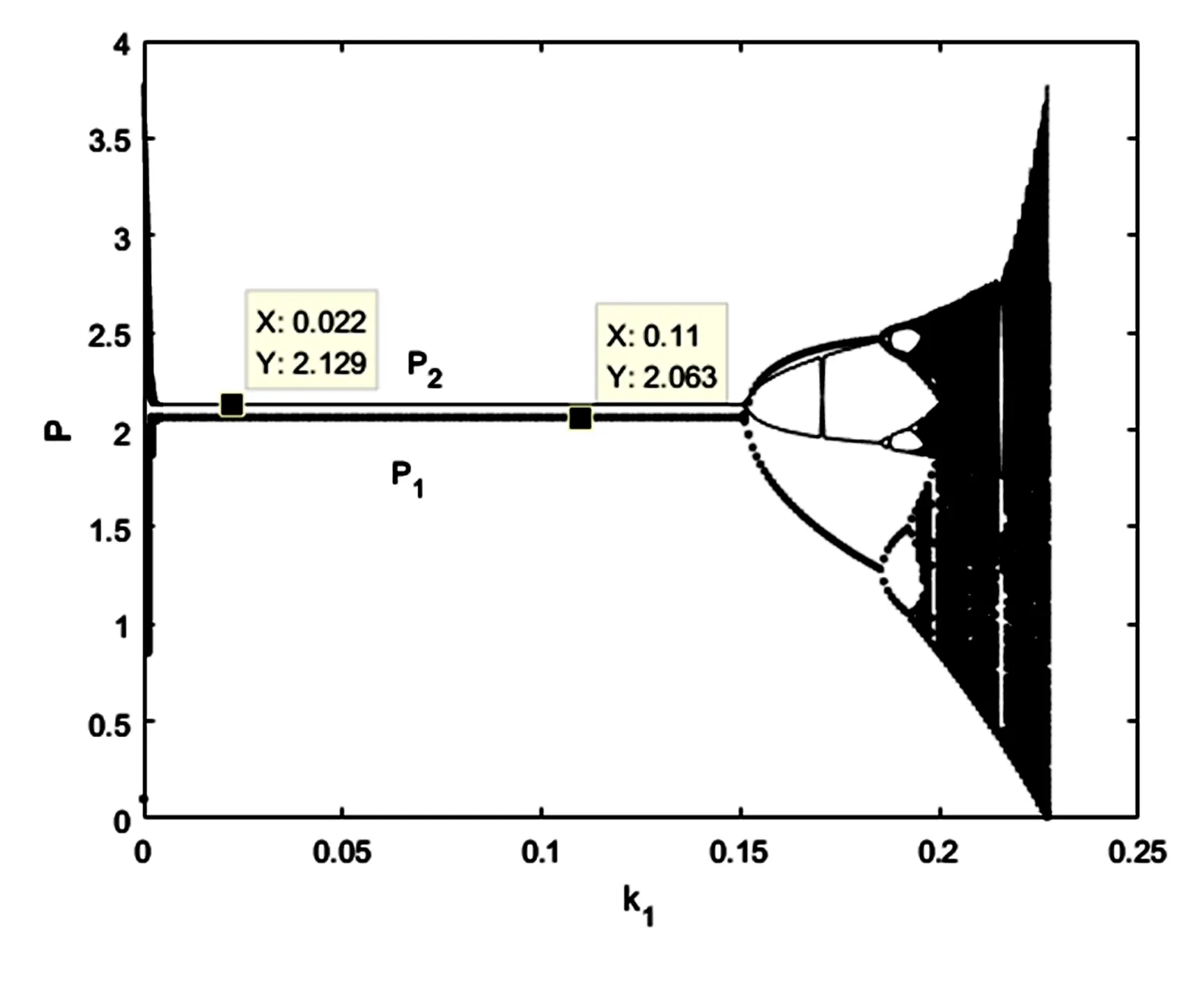
图1 调节速度k1对于价格P1和P2的影响Fig.1 Influence of the regulation speed k1on the price P1and P2
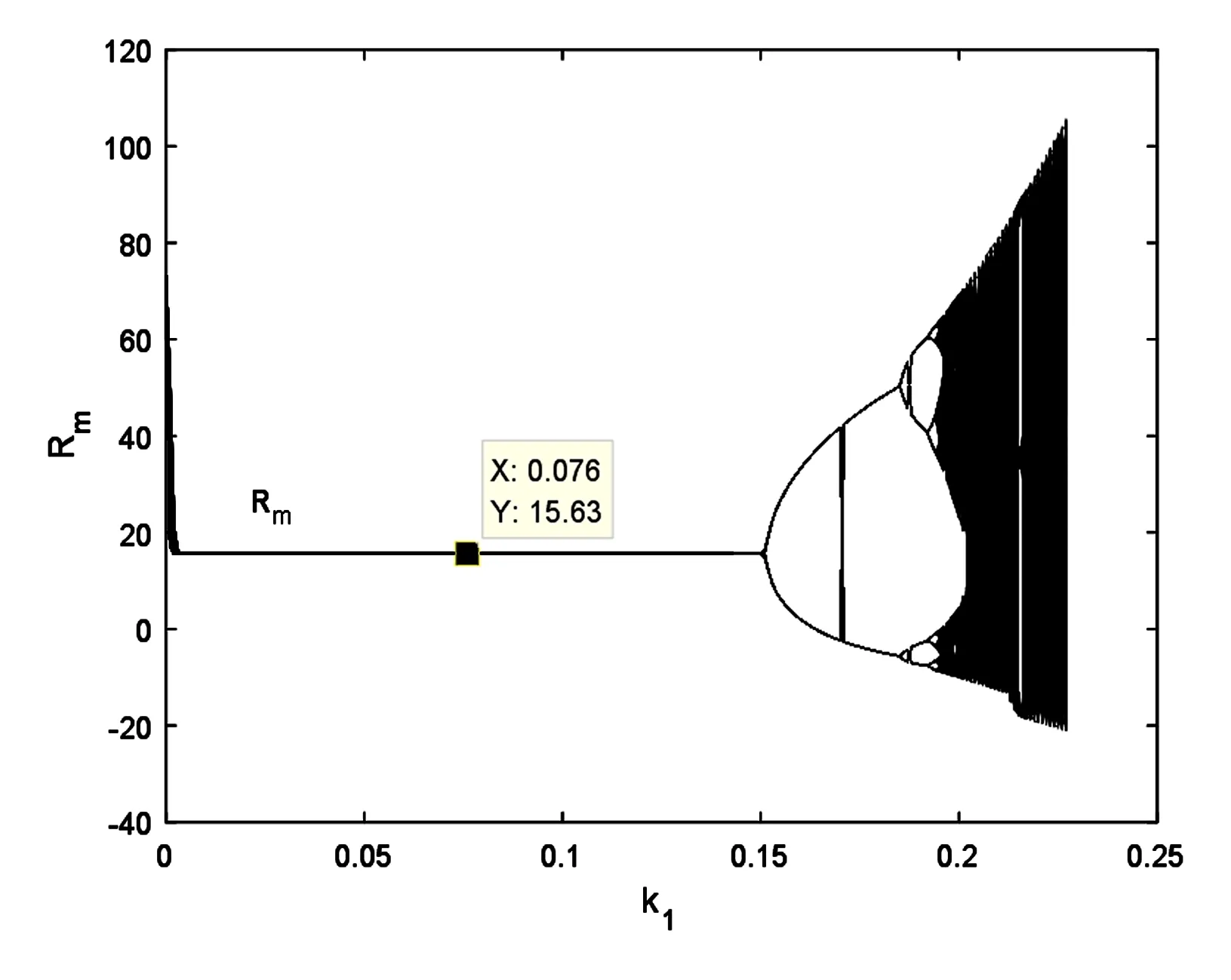
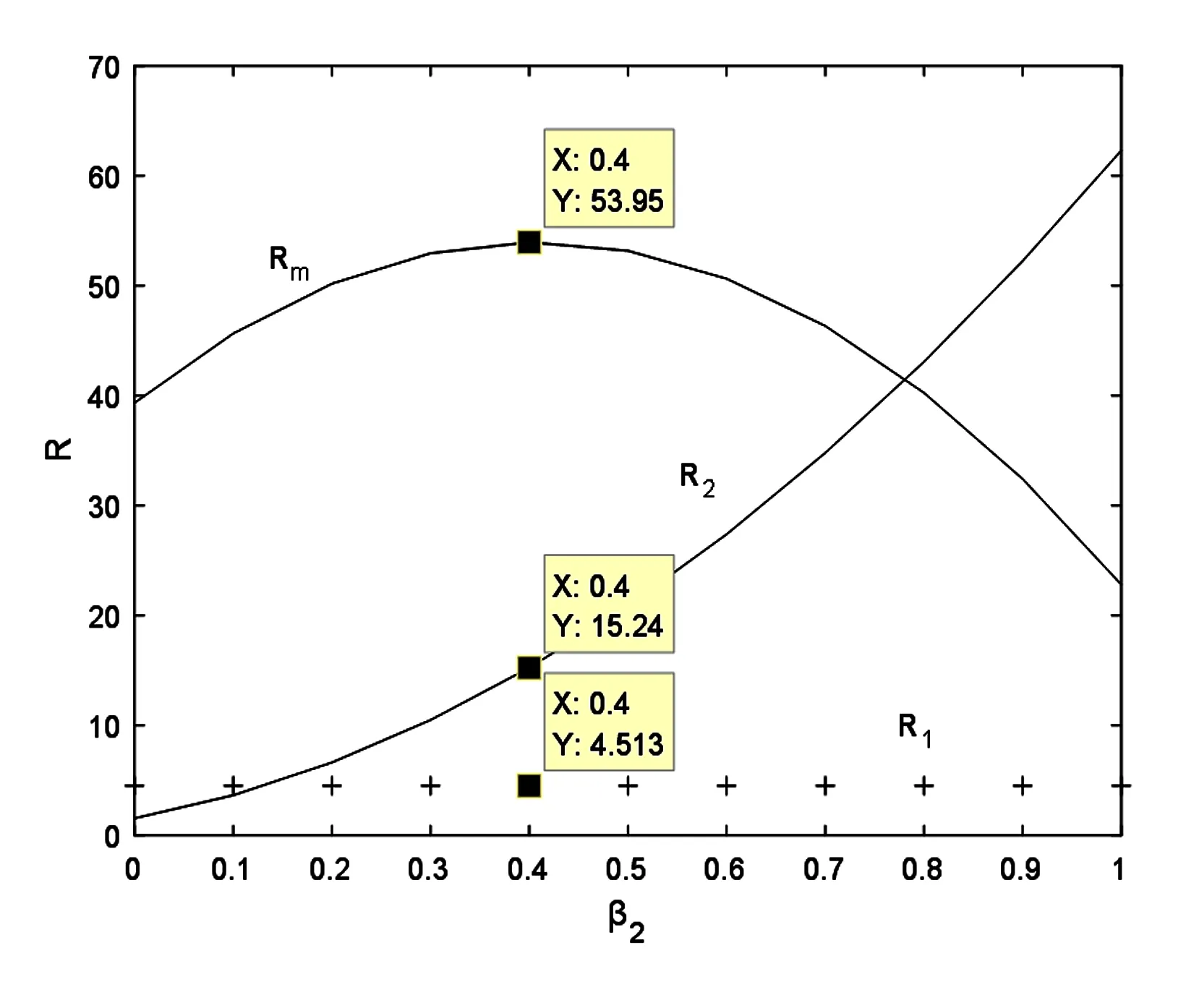
从图1可以看出,当0 图2 调节速度k1对于供应商利益R1和R2的影响Fig.2 Influence of the regulation speed k1on the supplier interests R1and R2 图3 调节速度k1对于主制造商利益Rm的影响Fig.3 Influence of the regulation speed k1on the main manufacturer interest Rm 图2与图3分别表示随着k1的变化,两个供应商和主制造商利益的变化,可以看到,在稳定状态下,供应商一的利益略高于供应商二的利益,当系统进入混沌状态后,供应商和主制造商的利益均会有较大的波动状态. 以上分析可知,两个供应商应将价格调整速度保持在0~0.15之间,价格始终稳定在纳什均衡点上,系统也处于稳定状态. 在共生利益分配模型中,主制造商引导两个供应商降低产品价格,然后根据供应商价格的降低程度将获得的利润按照一定的比例分配给供应商,以此实现各自利益的提升.由于供应商价格的降低,此时假设主制造商的成本变为p′=8.由假设3可知,主制造商在共生利润分配后,利益得到了提升.由此可知: (w-p)(Q1+Q2)< (1-β1)(w-p′)Q1+ (1-β2)(w-p′)Q2 (8) 带入上述数值,可得如下约束: (9) 因此,只要β1和β2满足上述不等式关系,则相对于共生前,主制造商的利益在共生利润分配后是增长的. 考虑上述条件,令β1=0.2,β2=0.3,得出调节速度k1对于价格p1和p2的影响,如图4所示,可以发现:当0 图4 调节速度k1对于价格P1和P2的影响Fig.4 Influence of the regulation speed k1on the price P1and P2 图5表示共生利润分配下,供应商一的价格调整速度对主制造商和两个供应商利益的影响.可以看出,利益均明显升高,此时,由于供应商二的价格下降较多,主制造商对于供应商二的补贴也较多,供应商二的利益略高于供应商一,由此激励了供应商的积极性,使得整个供应链系统更加稳定. 图5 调节速度k1对于供应商和主制造商利益R1、R2、Rm的影响Fig.5 Influence of the regulation speed k1on the supplier and main manufacturer interests R1、R2、Rm 令β2=0.3,考虑纳什均衡情况下,主制造商和两个供应商利益的变动情况,如图6所示,主制造商的利益变化先增后减,而两个供应商利益则呈上升趋势,当β1=0.6时,主制造商的利益达到最大. 图6 共生利益分配系数β1对于供应商和主制造商利益R1、R2、Rm的影响Fig.6 Influence of symbiosis benefit distribution coefficient β1on the suppliers and main manufacturer interests R1、R2、Rm 令β1=0.2,图7表明了β2对于三方利益的影响,此时共生系数β2的变动对于供应商一的利益无影响,始终稳定在4.513上,而供应商二的利益呈现上升趋势,主制造商的利益则是先增后减,当β2=0.4时,主制造商的利益达到最大. 图7 共生利益分配系数β2对于供应商和主制造商利益R1、R2、Rm的影响Fig.7 Influence of symbiosis benefit distribution coefficient β2on the suppliers and main manufacturer interests R1、R2、Rm 图8表示β1=0.2,β2=0.4时,供应商一的价格调整速度对于三方利益的影响,可以发现,此时稳定情况下,三方的利益情况与上述分析一致,主制造商的利益实现了最大化,两个供应商的利益也得到了提高. 图8 调节速度k1对于供应商和主制造商利益R1、R2、Rm的影响Fig.8 Influence of the regulation speed k1on the supplier and main manufacturer interests R1、R2、Rm 上述分析可知:两个供应商在主制造商的引导下,降低产品价格,主制造商由此可以获得更高的利益,而为了激励供应商,主制造商将所得的利益按照一定的比例分配给供应商,由此实现利益的共同增长.与基本模型相比,在共生利益分配模型下,供应商的价格调整速度保持在0到0.25之间,稳定区域实现了增加,两个供应商的价格维持在(1.313,1.182)上,供应商与主制造商的利益均得到了有效的提升. 本文研究一个主制造商和两个供应商的价格博弈问题.根据主制造商供应商的共生伙伴关系,引入共生系数,分析了基本模型与共生利润分配模型下,价格调整速度对于系统稳定以及企业利益的影响.研究发现:复杂产品协同制造下,主制造商和供应商在产品定价时,为了追求个体利益的最大化,会不断调整价格来达到自己的目的.随着双方价格调整速度的增加,供应链系统的稳定性也随之改变.价格调整速度越快,超过稳定范围,供应链系统便进入混沌状态.这从理论上表明,为了维持整个供应链的稳定,促进长期合作,主制造商和供应商应当适当地控制自身的价格调整速度.此外,由于双方的共生特性,引入共生利润分配,发现可以增加整个系统的稳定情况.主制造商作为主导者,通过引导供应商降低产品价格,并且将由此得到的利润通过一定的比例补偿给供应商,最终主制造商和供应商均能获得较高的利润,由此可以激励供应商的积极性,提高企业的利益,增强系统的稳定.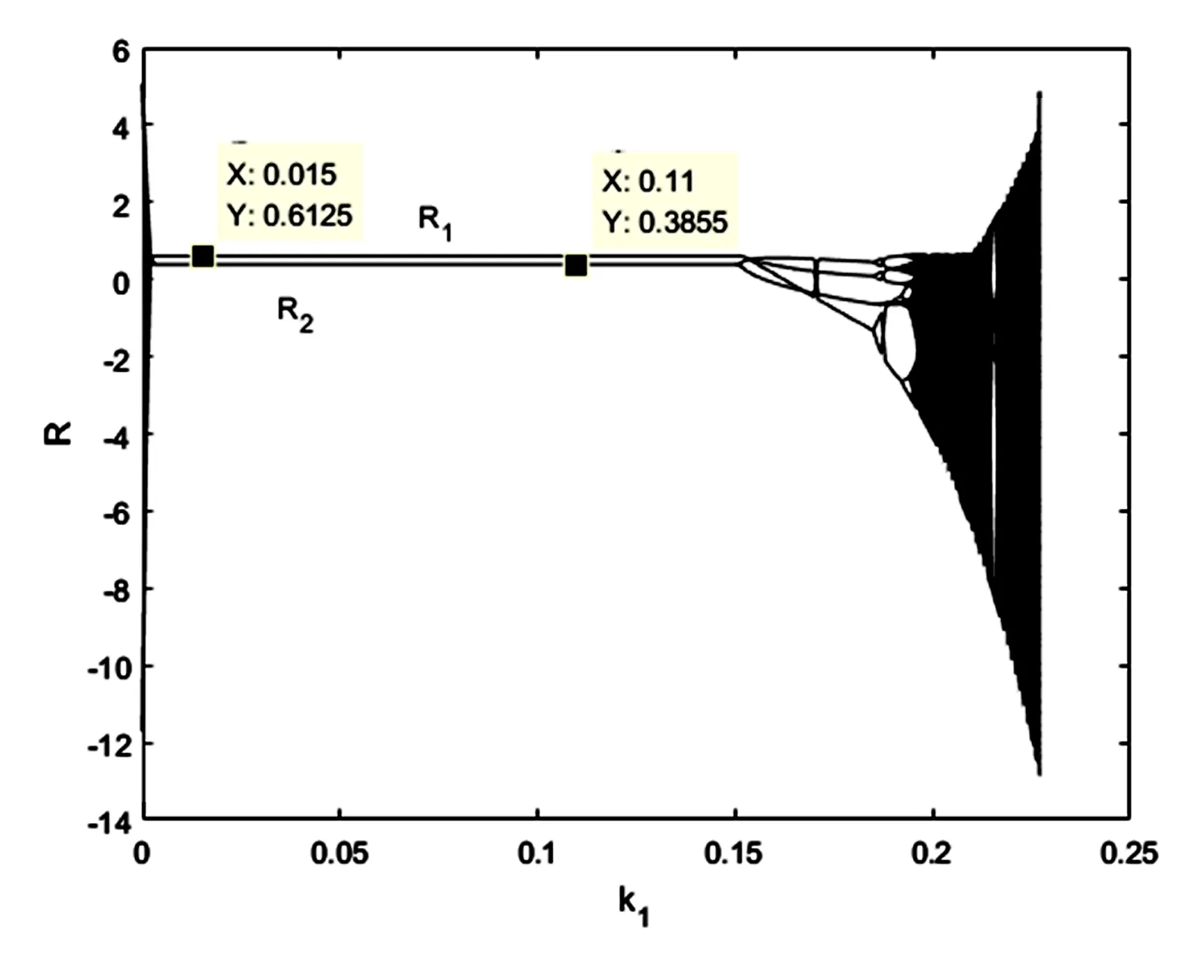
3.2 共生利益分配模型




4 结论

