一类弦-梁耦合非线性振动系统的动力学数值模拟研究*
吴娟 钱有华
(浙江师范大学 数理与信息工程学院, 金华 321004)
引言
非线性系统自被提出以来一直都是非常具有吸引力和发展前景的研究领域.然而随着深入的研究,人们发现许多实际系统中存在激励振动而不能用传统自由振动和受迫振动模型进行模拟,为了解决这个问题在文献[1-4]分别建立了激励系统的非线性模型,并对模型进行相关研究.另外越来越多的研究表明共振能够反映系统线性模态之间的相互作用,有着非常重要的研究价值.文献[5]通过研究弹性悬浮电缆模型的共振,构建了该模型在1∶1主共振和1∶2亚谐共振情形下的非线性模态.文献[6]研究了一个极限环振子系统发生的1∶3共振的Hopf 分岔,并研究了非线性不同共振情形下对其动力学行为的影响.文献[7]研究了一个弦-梁模型的弦和梁在2∶1内共振且梁在主参数共振-1/2亚谐共振和弦在1∶1主共振情形下的非线性模态,并研究了外激励对共振附近动力学行为的影响.文献[8]研究了微谐振器模型在不同参数响应下的非线性模态.同时,研究者们已应用多种方法研究系统在共振点处的动力学行为,并取得了丰硕的成果:文献[9]应用多尺度方法研究了磁场力作用下的双稳态曲梁压电发电离散系统的动力学行为.文献[10]运用多尺度法研究了两自由度和三自由度下系统的高阶近似.文献[11]讨论了轴向加速运动粘弹性梁问题的稳定性,该文献主要运用多尺度法和数值方法.文献[12]利用多尺度法研究了高阶多参数模型的响应和稳态.上述研究基本上是运用多尺度方法.可以看到多尺度方法不仅能计算稳态响应和计算非稳态响应,还能分析稳态响应的稳定性.因此经常被用来求解非线性系统的近似理论解.除了多尺度法还有许多其它有效的方法来求解非线性系统的理论解.比如文献[13]应用平均法研究 Duffing-van der Pol系统的稳态响应,文献[14]应用摄动法分析了含有阻尼项的拟线性系统在噪声激励下的响应,文献[15]对单边碰撞悬臂梁系统,在基础激励实验中,变换多次激励频率运用实验法的定性研究.数值方法通过数值求解非线性微分方程得到非线性系统在特定的参数条件和初始条件下的运动规律.不仅具有检验理论结果的作用,还能得到直观的结果为理论研究提供启示.本篇文章继承了文献[7]的工作,但改变了系统的共振情况,增加应用多尺度方法微分方程定性理论研究了弦-梁耦合非线性振动系统的稳态与分叉,并进一步运用数值模拟分析了系统的运动情形.
文章结构如下:第一部分,介绍弦-梁耦合非线性振动系统模型.第二部分,对本文所研究梁和弦之间产生1∶1主共振,梁在主参数主共振下原系统的平均方程.第三部分,通过阻尼系数分析参数变化对系统稳态响应的影响.第四部分,用数值模拟探讨外激励下系统运动形式.第五部分,对全文研究内容进行总结概括.
1 模型介绍
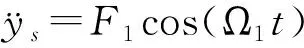

图1 模型图Fig.1 Model of a string-beam coupled system
由以上假设,运用弹性力学方法建立弦-梁耦合系统的非线性动力学方程为:
(1a)
(1b)
其中m1和m2分别为梁和弦单位长度质量,w1和w2分别是梁和弦的横向位移,l是梁和弦的长度,P0是梁两端所受的轴向压力,T0是弦的初始张力,A是梁变形前的横截面积,c1和c2分别是梁和弦的线性外阻尼系数,Ks是弦的弹性系数,E和I分别是梁的杨氏模量和转动惯量.
梁的边界条件:
弦的边界条件:
x=0,w2(0,t)=w1(0,t)
x=l,w2(l,t)=w1(l,t)
引入如下无量纲变量:

(2)
将上述变换代入方程(1),化简去掉(*),可以得到弦-梁耦合系统无量纲形式运动方程:

(3a)
α2l12y1-α2(g22l12+2g21l22)y22y1-α2g11l12y13-
(3b)
其中:

由于弦和梁的方程是耦合的,假设弦的模态函数包含有梁的相对位移,对梁和弦各取一阶模态进行Galerkin方法截断,梁和弦的位移w1和w2有如下形式
w1(x,t)=Y1(x)y1(t)
w2(x,t)=Y2(x)y2(t)+Y1(x)y1(t)
(4)
把式(4)代入无量纲形式弦-梁耦合系统运动方程,并且利用Galerkin方法进行截断,得到在参数激励和外激励联合作用下弦-梁耦合系统二自由度非线性常微分方程:
2β4g12l11y2y12=f11cosΩ1t
(5a)
(5b)
其中:
2 摄动分析
在本节中将运用多尺度方法分析方程(5).为了便于利用多尺度法对弦-梁耦合系统进行摄动分析,引入如下的尺度变换:
μ1→εμ1,a11→εa11,a13→εa13,a14→εa14
b21→εb21,b22→εb22,b23→εb23,a21→εa21
脉压雷达所采用的宽脉冲不仅可以提高雷达的平均发射功率,还能够确保足够大的作用距离。在接收端通过脉冲压缩处理将宽脉冲转化为窄脉冲,则可实现较好的距离分辨率,因此较好地解决了雷达大作用距离和高距离分辨率之间的矛盾。此外,脉冲压缩处理大大提高了雷达对非相干干扰的抑制能力[1]。如何对脉压雷达进行有效干扰已成为电子战领域的研究热点。
a24→εa24,f2→εf2,a22→εa22,a23→εa23
f11→εf11,f12→εf12
(6)
把变换代入上述得到含有小参数ε的运动方程:
εa13y12y2-εa14y13=εf11cosΩ1t
(7a)
εa21y23-εa22y1y22-εa23y12y2-
εa24y13=εf12cosΩ1t
(7b)

首先,令y1=y10+εy11,y2=y20+εy21并且引入导算子得:
(y10+εy11)+(Ω12+εσ1+εf2cos2Ω1t)-
εa13(y10+εy11)2(y20+εy21)-
εa14(y10+εy11)3=εf11cosΩ1t
(8a)
(y10+εy11)+εμ2(D0+εD1)(y20+εy21)+
εa22(1/9Ω12+εσ2)(y10+εy11)(y20+εy21)2-
εb22(D0+εD1)(y10+ey11)-εa24(y10+εy11)3+
εa23(y10+εy11)2(y20+εy21)=εf12cosΩ1t
(8b)
比较ε同次幂有:
ε0阶:
D02y10+ω12y10=0
(9a)
D02y20+ω22y20=0
(9b)
ε1阶:
D02y11+ω12y11=-2D0D1y10-f2y10cosΩ2t+
a11y10y202-μ1D0y10+a13y102y20+
a14y103+f11cosΩ1t
(10a)
D02y21+ω22y21=-2D0D1y20-b21D02y10-
μ2D0y20-b22D0y10+a23y102y20+a22y10y202+
b23y10+a21y203+a24y103+f12cosΩ1t
(10b)
由(9a),(9b)得:
(11a)
(11b)
代入(10a),(10b)整理得:
2iω1A1′)×eiT0ω1+a13A12A2eiT0(ω2+2ω1)+
cc+NST
(12a)
b23A1eiω1T0+b21ω12A1eiω1T0+a24A13e3iω1T0+
(12b)
由于系统的非线性运动控制方程中即含有平方非线性项也有立方非线性项,引入小参数ε,考虑梁和弦之间产生1∶1主共振,梁在主参数1∶1主共振情况.
(13)
这里的ω1和ω2是相应线性系统的第一阶和第二阶的固有频率,这里的σ1和σ2是调谐参数,为了简化分析,设Ω1=Ω2=1.
由多尺方法的应用[16]经过计算得到梁和弦耦合非线性系统直角坐标形式下的平均方程:
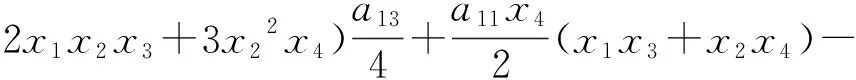
(14a)
(14b)
(14c)
(14d)
3 稳定性和分叉分析
根据运动稳定性理论,一个非线性系统稳定性取决于它的线性化系统,如果要分析非线性运动方程的稳定性,首先需要求出方程的平衡点.由方程(14)可知(x1,x2,x3,x4)=(0,0,0,0)为方程的平凡解, 对应的Jacobian矩阵为:
(15)
Jacobian矩阵(15)对应的特征多项式为:
f(λ)=a0λ4+a1λ3+a2λ2+a3λ+a4
(16)
其中:
a0=1
(17a)
a1=μ1+μ2
(17b)
(17c)
(17d)
(17e)
应用劳斯-霍尔维茨判据可知,如下条件均满足时:
a1>0,a1a2-a3>0
a1a2a3-a32-a12a4>0,a4>0
(18)
系统的所有特征值的实部均为负数,平衡点(x1,x2,x3,x4)=(0,0,0,0)是稳定的.如果(17)中有一个系数出现负值,那么系统有特征值实部出现正值,此时系统处在不稳定状态,将会导致分叉现象.因此,接下来我们会讨论系统的稳定性和分叉行为.
为分析阻尼参数对系统的稳定性的影响,取阻尼参数为分叉参数,通过计算假设参数值μ1=μ2=0,σ1=1.此时系统方程有双零和一对纯虚的特征值,则方程(15)的特征多项式和特征值为:
f(λ)=λ4+λ2,λ1,2=0,λ3,4=±i
(19)
选取μ1和μ2作为摄动参数,引入摄动变换μ1=ε1和μ2=ε2.则Jacobian矩阵(15)的特征多项式可以写成如下形式:
f(λ)=c0λ4+c1λ3+c2λ2+c3λ+c4
(20)
其中:
c1=ε1+ε2
(21a)
(21b)
(21c)
(21d)
由劳斯-霍尔维茨判据中平衡点是稳定条件可以将临界曲线定义为如下:
L1:ε1+ε2=0
(22a)
(22b)
20ε22-3ε12ε22-14ε1ε23-2ε24)=0
(22c)
通过上式可以画平衡点的分叉曲线,如图2.临界曲线L1、L2、L3将平面(ε1,ε2) 分成稳定区域和不稳定区域,其中Ⅰ为稳定区域,Ⅱ为不稳定区域.
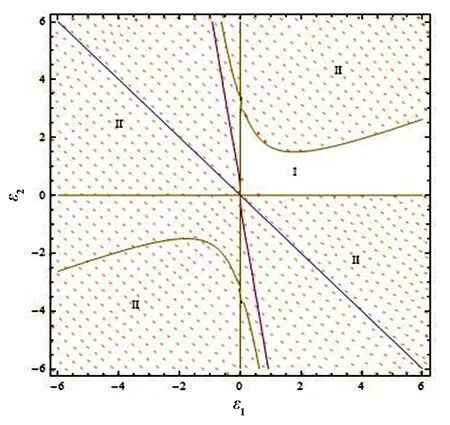
图2 双零和一对纯虚特征值的稳定以及不稳定区域Fig.2 Stable region and unstable region for the case of a double zero and a pair of purely imaginary eigenvalues
为了验证理论分析,在不同区域选取不同的参数值.首先,选取参数(ε1,ε2)=(0.5,0.1)在稳定区域Ⅰ中(z1,z2,z3,z4)=(0.004,0.01,0.003,0.001),我们得到图3. 在图3中,相空间轨线从初始点逐渐盘旋趋于平衡点达到稳定状态.选取(ε1,ε2)=(-0.5,0.2)在不稳定区域II中和(z1,z2,z3,z4)=(0.0005,0.001,-0.01,0.001),得到图4.相轨迹为不断向外扩展的螺线.
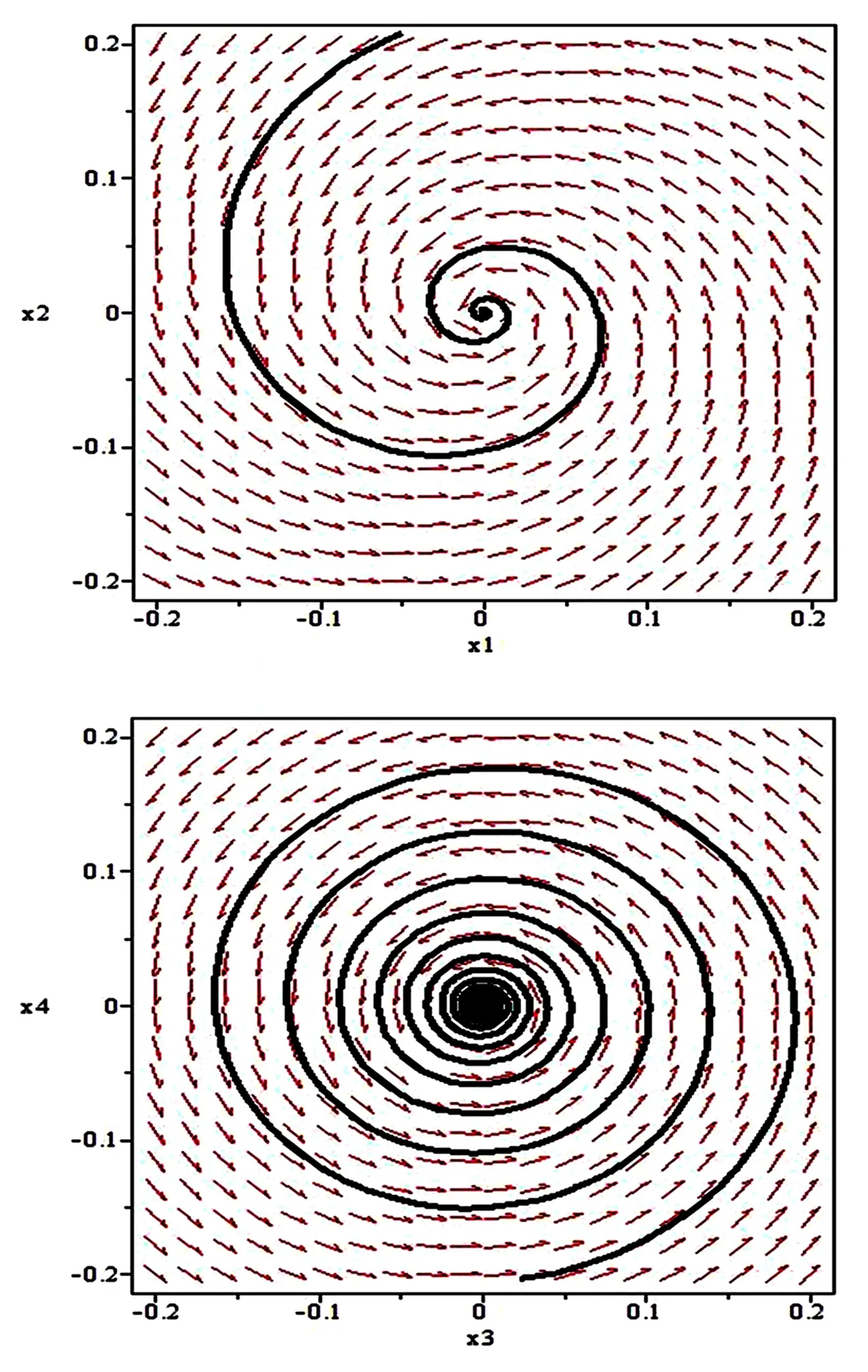
图3 稳定区域内的轨迹Fig.3 Trajectory of the stable region

图4 不稳定区域内的轨迹Fig.4 Trajectory of the unstable region
4 数值模拟
为了对平均方程进一步研究利用四阶龙格-库塔算法[17]发现了弦-梁耦合系统混沌运动的存在.设方程(14)中的基本参数为a11=20.1,a13=40,a14=56.2,a21=101.425,a21=10,a23=-13.825,a24=-3.8,b21=15,b22=27,μ1=0.88,μ2=0.0016,f12=42 对外激励f11赋予不同的数值,由matlab作图得到图5~8的不同的运动情形.其中,(a),(b)分别为x1,x2和x3,x4相图,(c),(d)分别为x1和x3的时间历程图,(e)为x1,x2,x3的三维相图,(f)为庞加莱截面图.

图5 单倍周期解(f11=50.8999)Fig.5 Period-1 solution when f11=50.8999
当外激励f11=50.8999时,如图5(f)所示系统庞加莱截面只有一个孤立的点,可判断此时弦-梁耦合系统产生单倍周期运动. 当外激励改变为f11=180时,如图6此时弦-梁耦合系统产生两倍周期运动. 当外激励f11=58.0582时,如图7系统产生四倍周期运动. 当改变外激励为f11=5.44时,图8(f)给出的庞加莱截面表明弦-梁耦合系统产生混沌运动.同样的,从 5(e)、6(e)、7(e)和8(e)可看出系统的运动情形,因为轨道的跳跃发生在三维相图中.
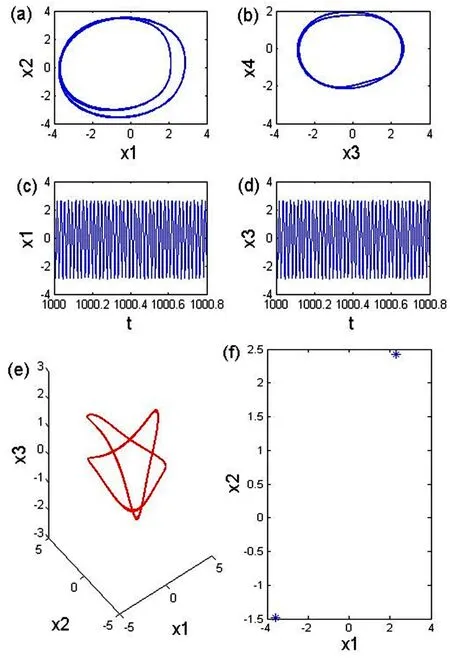
图6 二倍周期解(f11=180)Fig.6 Period-2 solution when f11=180

图7 四倍周期解(f11=58.0582)Fig.7 Period-4 solution when f11=58.0582

图8 混沌运动(f11=5.44)Fig.8 Chaotic motion when f11=5.44
5 结论
文献[7]中用Galerkin方法,得到了弦-梁耦合系统的运动控制方程,进而简化为具有两自由度的常微分方程.本文运用解析和数值方法研究了一种基于参数和外部激励的弦-梁耦合系统的稳定性与分叉和混沌动力学.利用多尺度法,求得具有参数和外部激励系统的平均方程.本研究的重点是在梁和弦的模式之间存在1∶1内部共振的情况,这是弦的主参数共振和梁的主共振.在平均方程的基础上,对系统的稳定性进行分析,发现参数取某些值时有系统一个双零和一对纯虚特征值.分叉分析结果表明,该弦-梁耦合系统具有稳定的平衡点.为了进一步说明理论预测,利用四阶龙格-库塔算法进行数值模拟.绘制平面相图时间历程图、三维相图和庞加莱图.数值结果表明,该系统的混沌响应有不同的形状.研究还发现:外激励参数f11对弦-梁耦合系统的混沌运动有重要影响.

