一种基于几何力学的机械臂末端规划算法
王本亮 高山 孙宏伟 史东华
(1.北京理工大学 数学与统计学院, 北京 100081) (2.复杂信息数学表征分析与应用北京市重点实验室, 北京 100081)(3.中国船舶重工集团公司第七一六研究所, 连云港 222006)
引言
随着工业机器人应用范围的扩展,机器人在导航、搬运、装配、喷涂与焊接场景中与人交互工作的情况越来越多,如何避免与人及障碍发生碰撞成为机器人运动规划中的一个重要问题.目前运动规划中对避障的处理可分为全局规划与反应规划两种方式[1].
全局规划通常采用概率方法, 尽可能找到一条从运动起点到目标终点的无碰撞轨迹, 再利用样条函数将轨迹光滑化. 常用的有Kuffner和LaValle[2]提出的一种基于采样的路径规划算法—RRT(快速随机生成树), 其通过对状态空间中的随机采样点进行碰撞检测, 从起始位置快速扩张树来规划路径. Karaman和Frazzoli等[3]提出了RRT*法, 并证明在一定条件下, 该方法以概率1收敛到最优解. 这类基于采样的规划算法通常应用于已知的作业环境中, 适合解决高维空间中多自由度、约束复杂的规划问题, 但存在实时性与可重复性较差、碰撞检测频繁等缺陷. 此外, 还可应用最优控制方法来规划从起始点到目标点的无碰撞最优路径(如最省时间, 最省能量等), 如Gerdts等[4]应用SQP(序列二次规划)法来求解多连杆机器人路径规划的最优控制问题, 并引入隐面剔除策略来减少求解过程中障碍带来的约束. 这类计算方法由于计算复杂度高, 难以实时实现.
反应规划通常利用机械臂连杆到障碍物的距离信息来实现避障. 由Khatib[5]提出的人工势场法是机器人反应规划最常用的一个方法: 机器人在一个虚拟的力场中运动, 障碍物与其它机器人个体设为斥力极, 目标点设为引力极, 机器人个体根据力场的综合作用来实现无碰撞轨迹规划, 但由于引力场和斥力场的相互作用, 易使机器人陷于局部极小(零势场)点处. Luo等[1]利用障碍物与机械臂间的斥力矢量信息构造计算简单的一阶运动方程实现避障, 但所生成的轨迹欠光滑. Chang和Marsden[6]提出了平面质点躲避凸障碍的回转力控制算法, 与势场法中的斥力极相比, 回转力总是垂直于机器人的速度, 该性质保证了由势场力梯度决定的控制律的收敛性. Garimella等[7]在此基础上提出了三维空间欠驱动系统避障的回转力方法.
几何力学以微分几何与对称性方法[8]为工具来研究力学系统的动力学与控制问题. 作为科学最古老分支之一的经典力学与数学中的微分几何、李群李代数等分支逐步携手, 形成了使用微分几何中的无坐标语言描述、兼具优美和广泛性的现代拉格朗日和哈密顿力学, 为多体系统、流体、场论及几何控制理论等提供了统一的框架. 我国学者在基于几何力学的非完整场论及约化、力学系统控制、保结构算法等方面取得了大量原创性的成果[9-12].
利用微分几何语言对机械臂建模的优势在于: 首先, 可得到描述运动且独立于坐标选取的最简洁运动方程; 其次, 能利用系统对称性进行约化, 并使约化后的系统便于构造理想的控制律; 最后, 还可利用几何结构的类似, 方便地将有限维连续系统的结构推广至无穷维力学系统, 从而可应用于软体机器人的建模仿真控制算法.
为克服上述算法存在的效率低、运动规划轨迹欠光滑等缺陷, 本文考虑开链机械臂末端避障的路径规划问题, 提出一种基于几何力学的反应规划算法. 本文第一节利用回转力实现机械臂末端刚体避障, 同时给出到达指定位姿的控制律, 进而获得光滑的避障轨迹; 第二节引入几何力学框架下的阻尼最小二乘法求解对应的机械臂逆运动学问题; 第三节将所得算法与特殊欧式群SE(3)中的RRT算法作对比. 最后以六轴开链机械臂为例, 给出相应的仿真实验结果.
1 机械臂末端避障的回转力方法
考虑机械臂末端刚体, 其质量为m, 转动惯量为, 位形空间SE(3)=SO(3)3, 位置x=(x,y,z)T∈3, 旋转姿态矩阵R∈SO(3), 体角速度为ω=(ωx,ωy,ωz)T∈3, 并记状态空间Q=TSE(3)≃SE(3)×se(3), 状态
假设控制u所在有界控制输入集为U, 定义控制力矩τ:Q×U→3, 作用力f:Q×U→3, 受控刚体运动方程可以写为:
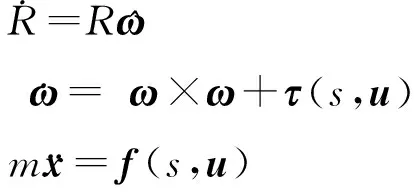
(1)
其中·^:3→so(3)为帽子映射:

(2)
(3)
其中Kx,Kv∈3×3为正定矩阵, Δx=x-xg为误差项,Γ(s)为斜对称矩阵.

(4)

为使位置控制律具有避障性, Garimella等[7]提出Γ(s)的一种设计方法:
(5)
其中Γi,k1(θi),k2(di),ei(s)为对应障碍物Oi的避障矩阵、角度系数、距离系数和旋转轴, 障碍物可视为一系列圆柱、球及其组合. 为简单起见, 假设单个障碍物为球形(若单个障碍物为圆柱, 旋转轴e(s)可取为圆柱的中心轴), 其半径为r,d为刚体质心位置指向球心的向量,θ为刚体质心运动方向与d之间的夹角,rd为检测半径. 取:
(6)
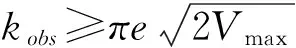
(7)
同样的, 为使目标姿态Rg可达, 可选取姿态控制律[13]:
τ= -skew(KRΔR)∨-Kω(ω-ΔRTωg)+
ω×(ΔRTωg)+
(8)
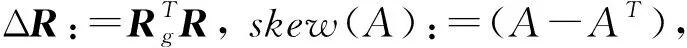
结合位置控制律和姿态控制律, 可获得刚体在SE(3)中到达指定位姿的无碰撞轨迹c=(R,x):[0,t]→SE(3).
2 运动学逆解的阻尼最小二乘法
从机械的角度看, 对于n连杆开链机械臂, 我们可以用一系列通过转动或移动关节连接的刚体运动链表示. 为简单起见, 只考虑转动情形. 此时关节空间Tn是各独立关节角所在空间S1的n重笛卡尔积. 考虑机械臂由关节空间到工作空间的正运动学映射gst:Tn→SE(3).
逆运动学问题的处理一般可采用分析法或数值法. 分析法利用机械臂特殊几何结构得到解析表达式; 数值法通过迭代收敛得到局部的唯一解, 比较著名的算法有循环坐标下降法(CCD)、启发式FABRIK策略; 还可将逆运动学问题转化为优化问题, 利用Newton法、梯度下降法、阻尼最小二乘法等优化算法进行求解(详见综述[14]).
阻尼最小二乘法[14]综合了Newton法以及梯度下降法的优点, 并改善了两者的不足. 为应用欧式空间的阻尼最小二乘法(DLS), 我们利用局部微分同胚ψ:se(3)→SE(3)的逆映射将SE(3)中的逆问题转换到欧式空间se(3)中.
设cg:[0,t]→SE(3)为期望目标曲线, 令:
F(θ,t)=ψ-1(cg(t)-1gst(θ))
(9)
其中ψ可由指数映射或作为其近似的Cayley变换给出. 利用SE(3)中的Cayley变换[15]:
ψ-1(M)=(Cay-1(R),(R+I3)-1x)
(10)
其中,M=(R,x)∈SE(3),I3为3阶单位矩阵, Cay-1:SO(3)→so(3)为:
Cay-1(R)=(I3+R)-1(I3-R)
(11)
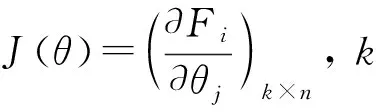
为求解F(θ,t)=0的最佳近似解, 考虑优化问题:
(12)
其中e=F(θ,t)为误差项,λ∈为非零阻尼系数. 阻尼最小二乘解为:
Δθ=JT(JJT+λ2I)-1e
(13)
当参数λ较小时, 算法效果趋近于Newton算法, 反之, 算法效果趋近于梯度下降法.
下面给出回转力避障与阻尼最小二乘法相结合的反应规划算法(算法I):

Algorithm I Reaction Planning
3 快速随机生成树(RRT)算法
为检验前面所提规划算法的有效性, 我们将其与经典的RRT算法进行仿真对比. RRT方法采样方式可分为关节空间采样[16]与工作空间采样[17]. 由于正运动学映射的非线性, 一般采用工作空间采样方式. Kuffner[18]介绍了刚体工作空间中常用的采样策略, 包括SE(3)采样点间距离的定义、插值方案的选取. 为实现在随机生成树中添加新路径, 即“长树枝”(图1)的过程, 我们利用前述阻尼最小二乘法生成采样点与RRT中父结点的连接路径.

图1 快速随机生成树算法示意图Fig.1 Representation of rapid-exploring random tree method (the extend operation)
具体实现过程为: 记初始位姿Q0∈SE(3)为随机树T根结点. 预先给定某阈值p(p∈(0,1]). 随机生成某数pc(pc∈(0,1)), 若pc≤p, 则在工作空间中随机采样, 采样点记为Qrand; 否则直接取定目标位姿为采样点Qrand.树T中距离Qrand最近的结点记为Qfather, 记由Qfather.x指向Qrand.x方向上步长为pstep处的结点为Qnew.x,Qnew.R可利用四元数与旋转矩阵的关系插值[18]给出. 其中Q*.x和Q*.R分别表示采样点Q*位置和姿态. 若机械臂位姿Qnew不与障碍物发生碰撞, 则将Qnew插入树T并连接Qnew与Qfather. 重复采样直至T到达目标位姿, 从而获得一条由Q0到目标位姿Qd的规划路径.
4 仿真研究
为验证我们所提出算法的有效性, 以简单的六轴开链机械臂为例(图2), 其杆长依次为l1,l2,…,l6, 对应质量为m1,m2,…,m6.
机器人运动学正解由指数积公式[19]给出:
(14)
其中机器人初始位姿:

(15)
运动旋量ξi:
(16)
其中ωi∈3是运动旋量轴线方向上的单位矢量, 定义为:
ω1=ω4=(0,0,1)T
ω2=ω3=ω5=(1,0,0)T
ω6=(0,1,0)T
(17)
qi∈3为轴线上的任一点, 取为:
(18)
将式(15)~式(18)代入式(14)得到机械臂正运动学映射. 在实验环境为Intel i5/2.5GHZ/2G的计算机上, 给定3组机械臂末端初始状态及可达目标状态, 分别采用RRT算法测试, 取偏向概率1-p=0.64, 步长pstep=2.8, 经样条函数光滑化, 得到轨迹如图3所示.

图2 六轴开链机械臂模型Fig.2 Model of six-axis open chain manipulator

图3 RRT规划算法所生成的避障轨迹Fig.3 Collision-free trajectories generated by the RRT path planning algorithm

图4 由回转力控制所生成的避障轨迹Fig.4 Collision-free trajectories generated by the gyroscopic force controller
为将算法I与RRT方法比较, 在相同场景下, 考虑开链机械臂末端实现避障, 取机械臂末端质量m6=3.92kg, 转动惯量=diag(2,2,1), 刚体初始及目标速度、体角速度均设为0, 得到轨迹如图4所示, 两种算法规划结果比较见表1.
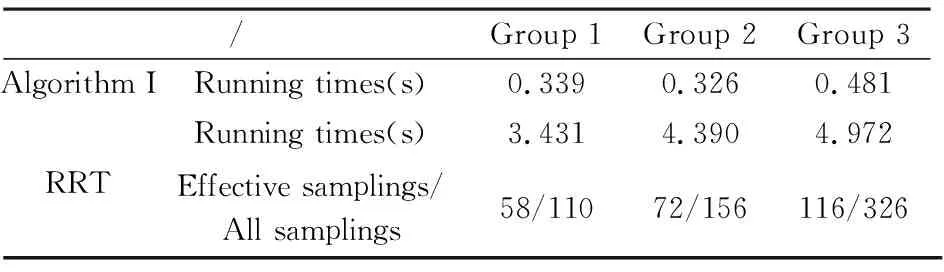
表1 算法I与RRT规划比较Table 1 Comparison of algorithm I and RRT planning
由上述结果可知:相比于RRT算法运行时间长、采样效率低, 回转力与阻尼最小二乘法的结合可达到快速避障的效果, 且无需用样条函数进行光滑化处理, 适用于一些末端追踪过程中快速避障的场景.
5 小结
本文提出了一种基于几何力学的开链n连杆机械臂末端规划算法, 借助末端刚体的自然运动方程, 分别引入势场力和回转力进行追踪与避障, 能够在工作空间中快速产生光滑的规划轨迹; 同时利用阻尼最小二乘法进行运动学逆问题的求解, 得到关节空间的规划路径, 可以克服传统算法检测频繁, 以及规划路径欠光滑等缺陷, 具有一定的实际应用价值.

