变截面粘弹性旋转梁非线性参数振动研究

张云飞 杨鄂川 李映辉†

(1.西南交通大学 力学与工程学院, 成都 610031) (2.重庆理工大学 机械工程学院, 重庆 400054)

引言

变截面梁在航空机械中有很多应用,对其振动特性和响应研究很多.Gupta等[1]用有限元法得到了截面直径线性变化的圆截面梁固有频率和模态；Heidebrecht[2]基于变截面梁振动方程用傅里叶级数法得到其固有频率和模态；崔灿等[3]提出了快速计算变截面梁振动特性的半解析法；Ghafari[4]用多项式降阶法得到旋转复合材料梁的固有频率.对粘弹性梁,杨晓东等[5]用多重尺度法研究了粘弹性变速运动梁的稳定性；Martin等[6]用修正变分迭代法对粘弹性梁进行分析,得到其振幅；Mahmood等[7]研究了粘弹性梁的非线性自由振动,得到阻尼对振幅的影响；Abolghasemi等[8]对不同倾角的旋转粘弹性梁进行研究,讨论了吸引子的稳定性；蒋宝坤等[9]对旋转粘弹性夹层梁的非线性自由振动特性进行了研究,得到其固有频率和响应.刘金建等[10]研究了轴向运动功能梯度粘弹性梁横向振动的稳定性,讨论了不同因素对稳定性的影响.目前对变截面粘弹性旋转梁的研究较少.Vinod等[11]提出了一种适用于有锥度的旋转欧拉梁谱单元的计算公式,验证了其正确性,并表明该单元在波传播问题中有更好的收敛性.Zolkiewski[12]研究了承受横向变载荷并且固定在刚性盘上的变截面梁的振动问题.朱由锋等[13]用有限差分法对变截面旋转梁的弯曲振动进行了研究,得到其幅频特性和相频特性.本文将基于Kelvin-Voigt粘弹性本构,考虑几何非线性建立其振动方程,研究其振动特性和参数振动,讨论其参数振动的稳定性.

1 数学模型

1.1 变截面粘弹性旋转梁模型

图1为高度随长度线性变化的变截面粘弹性旋转梁模型,刚性转毂半径R,梁左端高度a,右端高度为b,锥度Δ=b/a,长度l,宽度d,绕轮毂旋转角速度Ω,材料弹性模量E,粘性系数η,密度ρ.

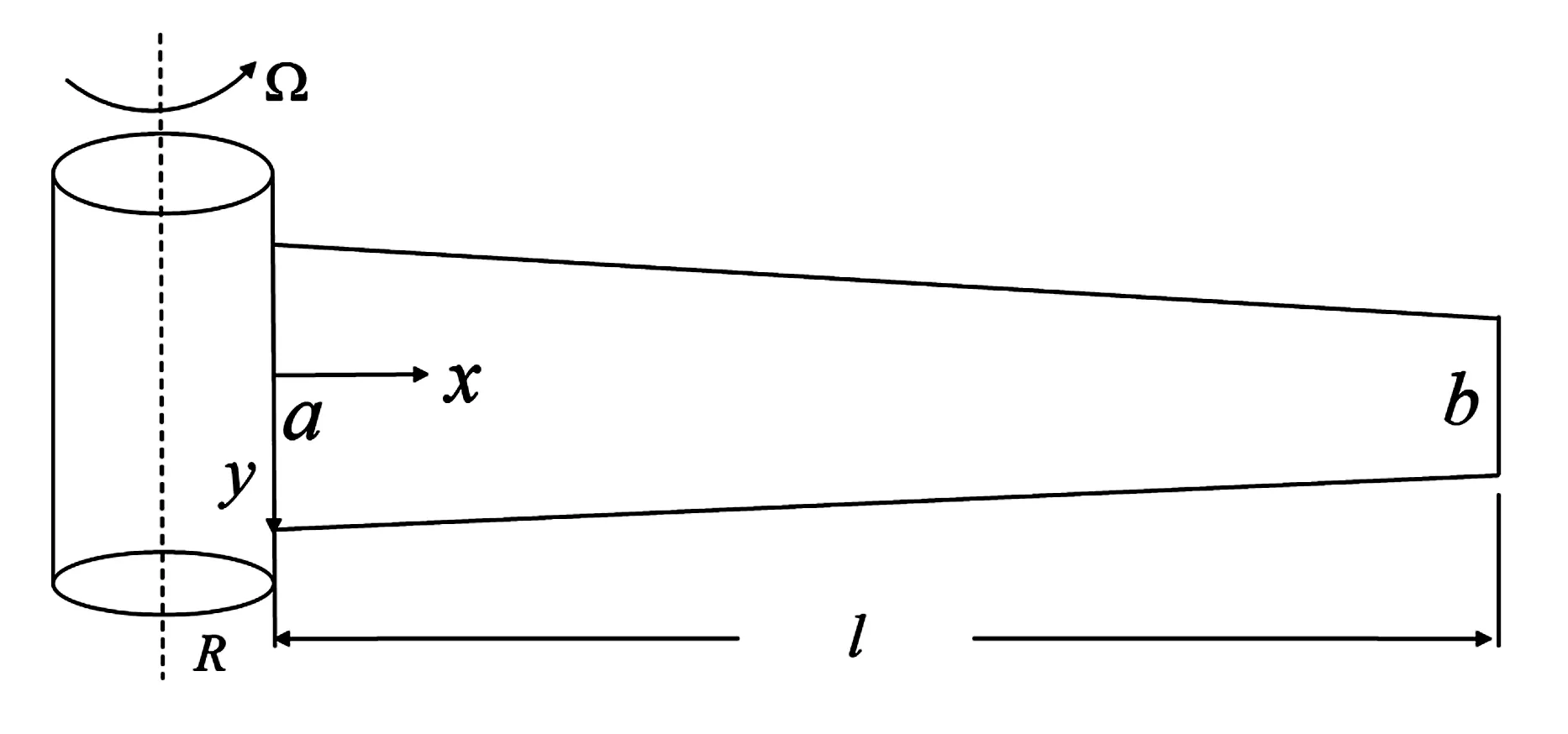
图1 变截面粘弹性旋转梁模型Fig.1 Rotating viscoelastic beam with variable cross-section

1.2 控制方程

仅考虑挥舞振动,旋转梁平衡方程[9]:

M,xx-ρAw,tt+(Nw,x),x=0

(1)

式中,M为弯矩,w为y方向挠度,A为横截面积,N为轴力,w,x和M,xx表示w和M对x的一阶、二阶偏导数,位于x处横截面积和惯性矩分别为:

对于粘弹性材料,用Kelvin-Voigt方程描述其本构关系:

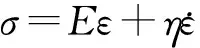
(2)

几何非线性关系:

(3)

离截面x处离心力为:

(4)

轴力为:

N=N1+∬Aσdydz

(5)

式(5)代入式(1)中得变截面粘弹性旋转梁非线性振动方程:

ηIw,xxxxt+EIw,xxxx+2EI,xw,xxx+EI,xxw,xx+

EAw,xxw,x+ηA,xw,xtw,x+ηA(w,xxw,xt+w,xw,xxt)-

(6)

边界条件为:

w(x,t)|x=0=w(x,t),x|x=0=0

w(x,t),xx|x=l=w(x,t),xxx|x=l=0

(7)

2 振动特性

方程(6)对应的线性振动方程为:

ηIw,xxxxt+EIw,xxxx+2EI,xw,xxx+EI,xxw,xx+

ηI,xxw,xxt+2ηI,xw,xxxt+ρAw.tt+

ρΩ2A(R+x)w,x-(ρΩ2AR(l-x)+

(8)

设:

(9)

其中,

Yi(x)= (cospix-coshpix)-

(10)

为满足边界条件的试函数,qi(t)为广义模态坐标,pi由方程(11)：

cosplcoshpl+1=0

(11)

确定,将方程(9)代入(8),基于Galerkin方法得：

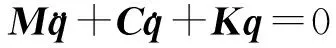
(12)

式中M,C,K为广义质量,阻尼和刚度矩阵,其元素为：

(13)

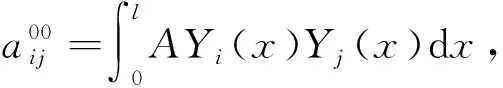
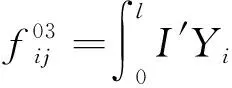
3 参数振动

在方程(9)中,取N=1,代入(6)有：

(14)

设：

Ω=Ω0+εcos(ωt)

(15)

式(15)代入式(14)有：

(16)

式中,

用多尺度法求解方程(16).

假设：

q1=q0+εq2

=D02+ε2D12+2εD0D1

(17)

代入(16)中得：

ε0项

D02q0+k1q0=0

(18)

ε1项：

D02q2+k1q2= -c1D0q0-2D0D1q0-

k2q0cos(ωt)-d1q03-g1q03D0q0

(19)

设q0解的形式为：

(20)

并令：

ω=2ω0+εσ

(21)

将方程(20)、(21)代入到(19)得：

k2(A(T1)eiω0T0+

d1([A(T1)]3e3iω0T0+3[A(T1)]2·

g1(iω0[A(T1)]3e3iω0T0+

(22)

消除(22)式久期项得：

(23)

(24)

得到：

(25)

令γ=σT1-2β,

(26)

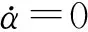
(27)

4 数值计算及讨论

本节通过数值方法讨论了梁的振动特性和幅频响应,计算中相关参数如表1.

表1 材料参数Table 1 Material parameters

4.1 方法有效性验证

为验证本方法,计算其频率并与有限元结果对比,有限元采用一维梁单元进行模拟,数值计算中取l=2m,a=0.1m,b=0.05m,d=0.05m,当模态阶数取12时,频率趋于稳定.表2给出了轮毂半径为0.1m,模态阶数为12时有限元法(FEM)及本文方法得到的不同转速下的前四阶频率.

表2 不同转速下的频率Table 2 Frequencies with various rotating speeds

可见有限元与本文方法有非常好的一致性,说明本文方法有效.

4.2 轮毂半径和转速对频率的影响

图2给出了转速、锥度和轮毂半径对一阶频率影响.

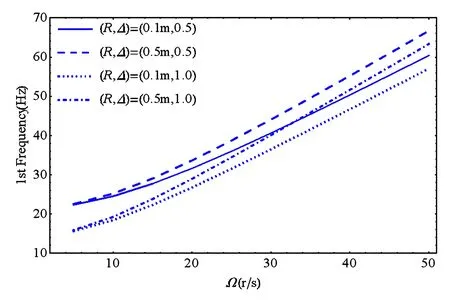
图2 一阶固有频率随转速、锥度和轮毂半径变化Fig.2 Development of first natural frequency with rotating speed, taper and radius of hub

可见,转速增大,频率增大,轮毂半径增大,频率增大,锥度增大,频率减小.

4.3 幅频响应

图3给出了轮毂半径为0.1m,锥度为0.25,转速为1r/s时的幅频响应曲线.图中实线和虚线分别代表系统的稳态和不稳态响应.可见系统从左到右存在两个分岔点,系统开始时只存在稳定的平凡零解,当到达第一分岔点时,系统发生音叉分岔,平凡解稳定性消失,出现一稳定的非平凡解,到达下一分岔点时,不稳定的平凡解变为稳定,同时分岔出一个不稳定的非平凡解.

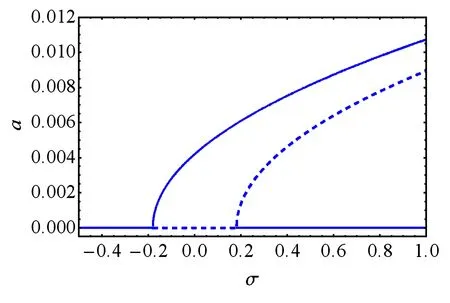
图3 幅频响应曲线Fig.3 Amplitude-frequency response curves

4.4 参数对稳定性的影响

图4给出了转速为1.0r/s,锥度为0.25,轮毂半径为0.1m和0.7m时的幅频响应曲线.可见轮毂半径增大,系统不稳定域增大.

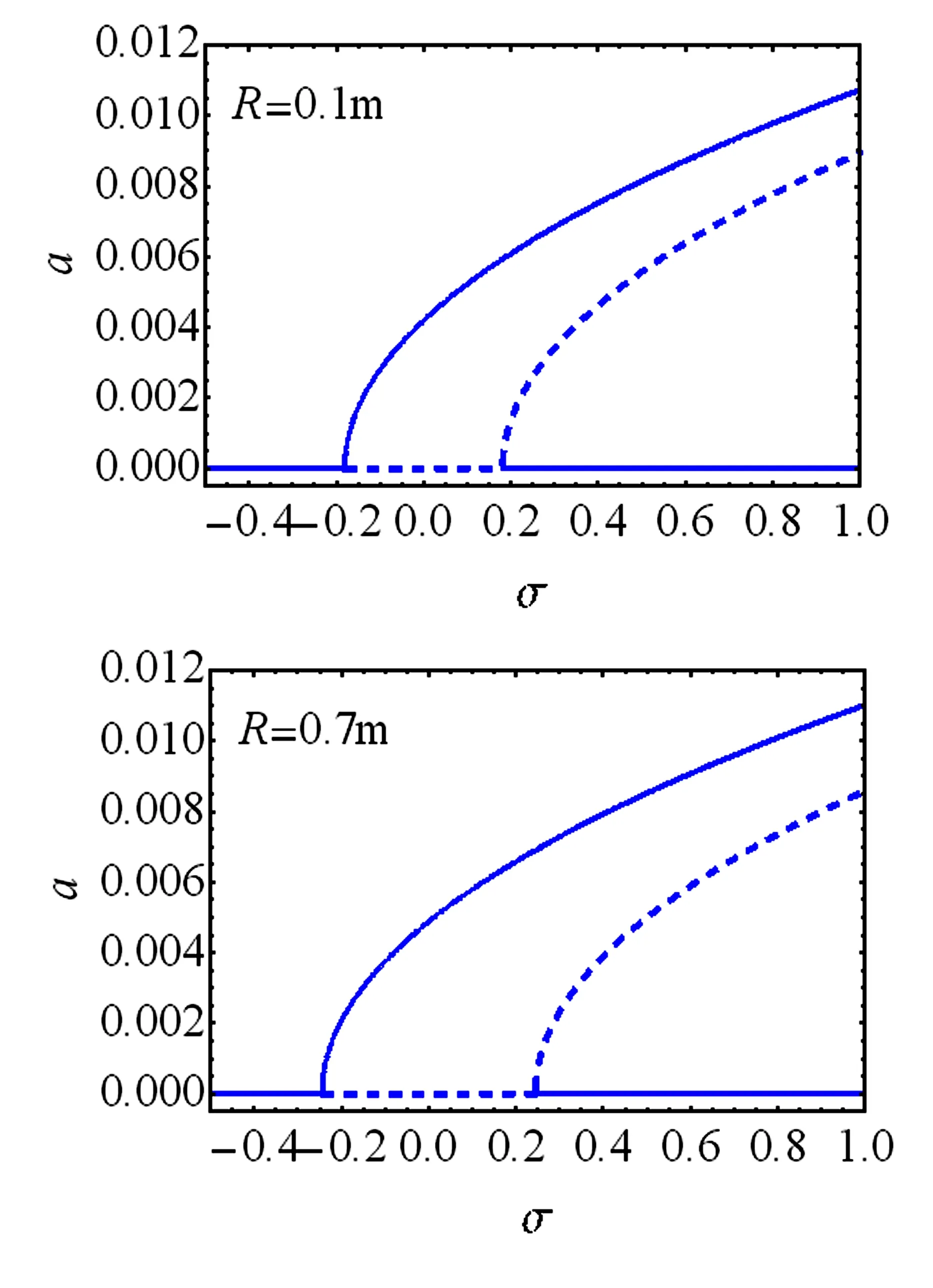
图4 轮毂半径对稳定性影响Fig.4 Effect of hub radius on stability

图5给出了轮毂半径为0.1m,锥度为0.25,转速为0.6r/s和1.2r/s时的幅频响应.可见随着转速增加,系统不稳定域增大,且使第一分岔点提前,第二分岔点延后.

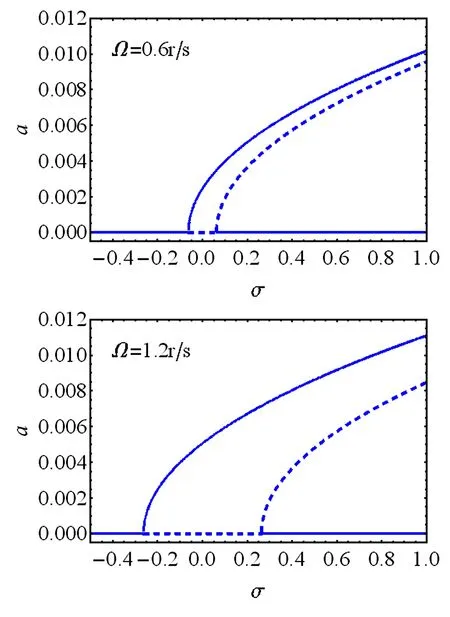
图5 转速对稳定性影响Fig.5 Effect of rotating speed on stability

图6给出了轮毂半径为0.1m,转速为1r/s,锥度为0.25和0.15时的幅频响应.可见随着锥度的增大,系统不稳定域减小.

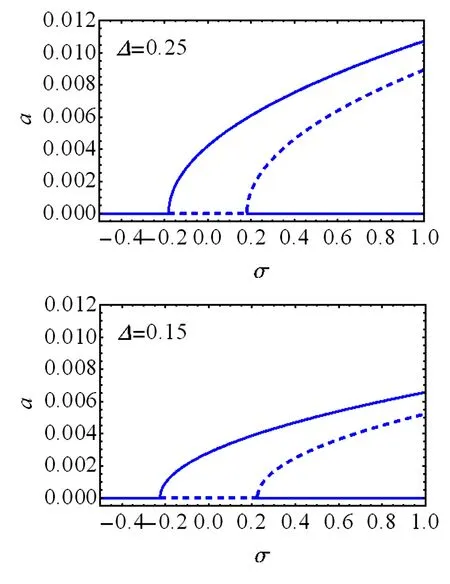
图6 锥度对稳定性影响Fig.6 Effect of taper on stability

5 结论

本文研究了变截面粘弹性旋转梁的振动特性和参数振动,得到了幅频响应.讨论了轮毂半径和转速对固有频率和幅频响应的影响,结果表明参数振动不稳定区域随轮毂半径、转速的增大而增大,随着锥度的增大而减小.