Fast Ferry Smoothing Motion via Intelligent PD Controller

Mounia Ticherfatine·Qidan Zhu

Abstract A novel type of control law was adopted to reduce the vertical acceleration of a fast ferry as well as the motion sickness incidence suffered by the passengers on board by means of a submerged T-foil.Considering the system changing characteristics under high disturbances,a model-free approach was adopted.In addition,an upgraded proportional-derivative(PD)controller with correction terms resulting from a fast-online estimation of the system dynamics was designed.The overall controller,known as intelligent PD(i-PD)controller,was tested, and the obtained results were compared with those of a classic PD controller. The controllers were also tested in a changing environment and at different operating velocities.The results confirmed the effectiveness of the i-PD controller to smooth the motions with low computational cost control schemes.Furthermore,thanks to ability of the i-PD controller to continually update the estimated dynamics of the system,it showed a better reduction in both vertical motions and the seasickness level of the passengers with the needed robustness under external disturbances and system changing parameters.

Keywords Model-free control . Intelligent PD . Pitchmotion . Ship control . T-foil . Smoothing motion

1 Introduction

Since the fast ferries and passengers comfort issues increase with increased speed, research studies have been conducted to reduce the undesirable effect of random sea wave disturbances on the vertical motions of the ships. Active fin stabilizers were then introduced on the ships to damp the effect of the forces of the vertical waves (Esteban et al. 2000). Moreover, the seasickness suffered from the passengers is related, in a cumulative form, to the vertical acceleration that is directly associated to the pitch motion induced by the forces and moments of the waves (O’Hanlon and MacCawley 1975).

Our research targets the improvement of the sea keeping of the fast ferries by means of an anti-pitching submerged moving device known as the T-foil.The regulation problem consists on designing an appropriate control law that can control the actuator to attenuate the vertical acceleration of the highspeed ferry.Thus far,classic PD controllers have been tested in the research studies of(Aranda et al.2001;Esteban et al.2002),and a fuzzy PD controller has been implemented to stabilize the vertical motion of the ship(Santos et al.2005).Later,a robust regulator-based-mixed sensitivity was designed to attenuate the vertical dynamic motions of the highly perturbed system(Ticherfatine and Qidan 2016).However,the design of the previously cited controllers was based on the linear model of the ship’s dynamics that can result in poor performances when tested in large operating domains and high order disturbances.To overcome these difficulties,model-free approach-based intelligent PD(i-PD)controller was adopted.

Recently introduced by(Fliess and Join 2009),model-free control is based on a local linear approximation of the system dynamics resulted from a fast model estimation technique.This approximation is continuously updated based only on the knowledge of the input-output attitude.

The control law is designed based on a PD controller augmented with compensating terms provided by the online estimation of the dynamics of the system.The resulting controller is known as intelligent PD.Adding more robustness to classic PD controllers with less mathematical complexity,model-free control was successfully applied to linear and nonlinear systems(Fliess et al.2011;Fliess and Join 2013).In this report,a model-free control based on i-PD controller is proposed to enhance the comfort of the passengers on the fast ferry by reducing the vertical motion using a submerged T-foil.To highlight the effectiveness of this strategy a comparison with a classic PD results is also performed.

This paper is organized as follows.First,the process model of a fast ferry equipped with a T-foil is presented.The sea waves and vertical acceleration effects on the seasickness level of passengers are introduced.Next,the proposed methodology of model-free control technique is explained and a fast estimation technique of the system dynamics is developed.An i-PD controller based on model-free control is then designed and applied to the system.Finally,the vertical motions and motion sickness incidence attenuations are tested and compared to those of a classical PD controller.

2 Process Model

The process model comprises the pitch motion model of a high-speed ferry equipped with the T-foil as an actuator with a control input u,and all are subjected to random waves’disturbances.

2.1 Ship Motion and Actuator

The vertical dynamics of the fast ferry are essentially related to pitch motion causing high vertical accelerations that are the main cause of seasickness suffered by the passengers on board.De la Cruz et al. established the model of pitch motion of a fast ferry by process identification(De la Cruz et al.2004).To counteract the effect of the wave’s forces and moments on the ship,a T-foil is placed on the bow as shown in Fig.1.

The T-foil is used as a stabilizer fin providing a lift force and moment to damp pitch motion induced by the wave’s effects on the hull.The main parameters of the used T-foil are listed in Table 1.The generated T-foil lift force and moment are a function of its angle of attack and the ferry’s speed described by the following equations(Aranda et al.2001):where CLis the lift coefficient,ρ is the fluid density,A is the area of the T-foil surface,δ is the angle of attack of the actuator,and x is the distance to the center of gravity(COG),where the T-foil is placed.

Fig.1 T-foil location on the ship

Table 1 The main parameters of the T-foil

A variation in the angle δ results in a generation of a lift forces and moments.The T-foil rotation angle is limited on[(-15°,15°)],and the rotational speed is limited to[(-13.5°/s,13.5°/s)](Esteban et al.2000).

The process model of the pitch motion of the ship equipped with the T-foil can be represented as shown in Fig.2.

The wave forces and moments acting on the hull are translated into pitch motions,and these forces are counteracted by the lift force generated by the actuator.

2.2 Waves Disturbances

In this study, Pierson-Moskowitz wave spectrum is adopted to generate the wave disturbances acting on the hull and is defined as follows:

where S(w)is the spectrum of the wave amplitude,w is the wave frequency,and h1/3is the significant wave height corresponding to a sea state number(SSN).

The amplitude of the resultant irregular wave can be obtained by the following equation:

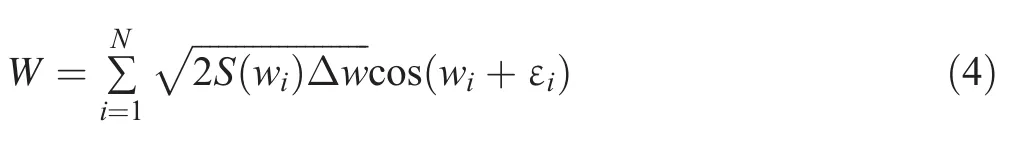
where εivaries from 0 to 2π which is the random phase angle of the irregular wave(Fossen 1994).

The pitching disturbance forces and moments acting on the hull are presented in Fig.3.The sea state number is chosen to be 4 with a significant wave height of 1.8 m.

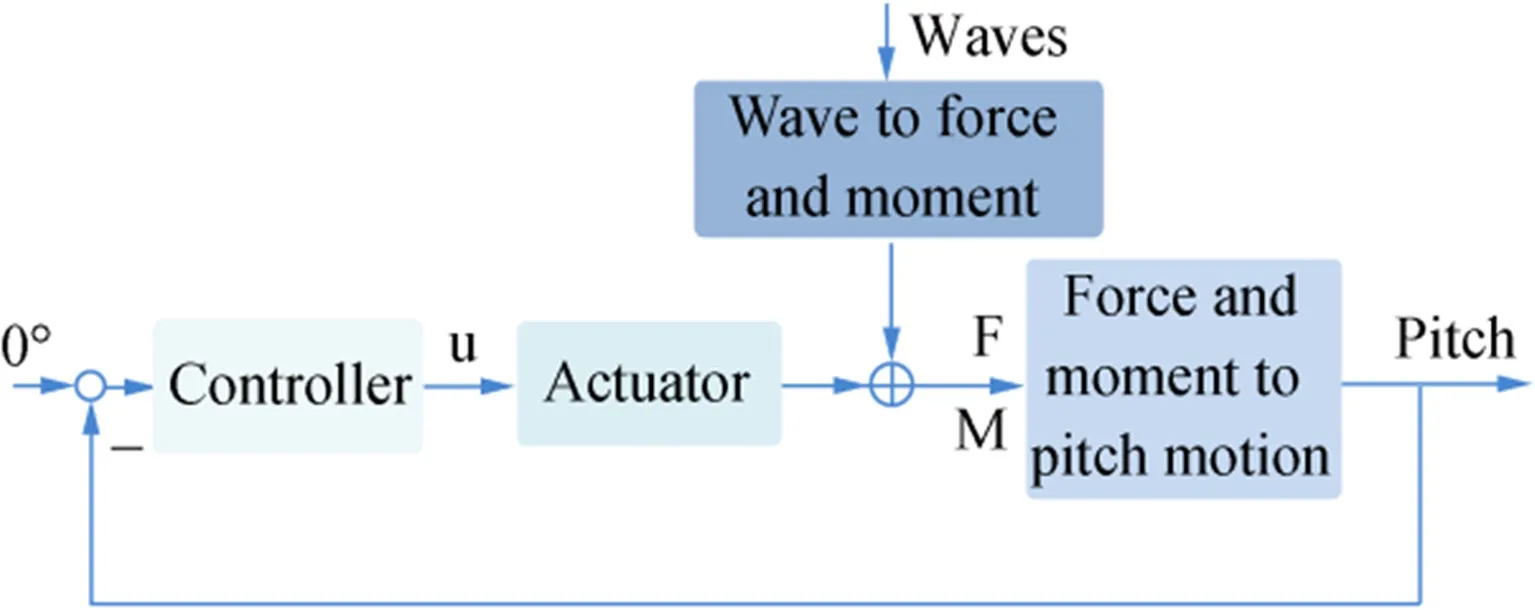
Fig.2 Process model of the ship with the T-foil under waves disturbances

Here,for instance,the transfer functions of the generated force(W2F)and moment(W2M)from wave height at a ship speed of 40 kn are as follows:

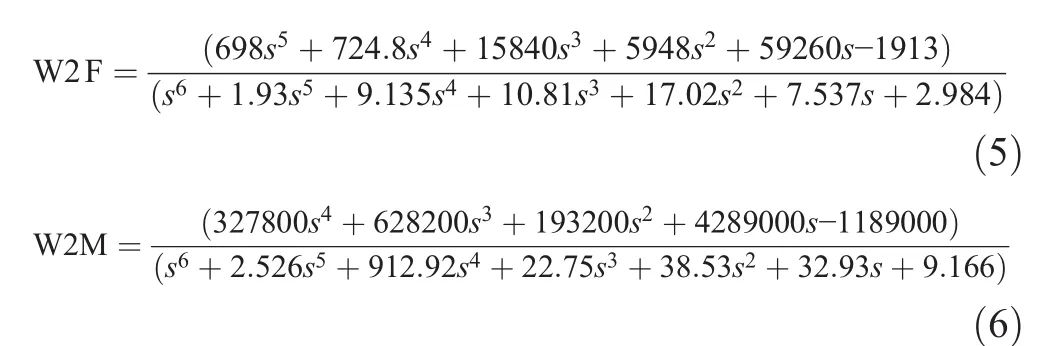
2.3 Vertical Acceleration and Motion Sickness

As previously mentioned,the pitch acceleration is the main cause for undesirable effects on the passengers.For the fast ferry,seasickness recorded its highest value originated from the vertical acceleration at 40 m forward from the COG,at that point,the pitch acceleration is the worst and it is called the “worst vertical acceleration”(WVA).The WVA can be computed by the following equation:

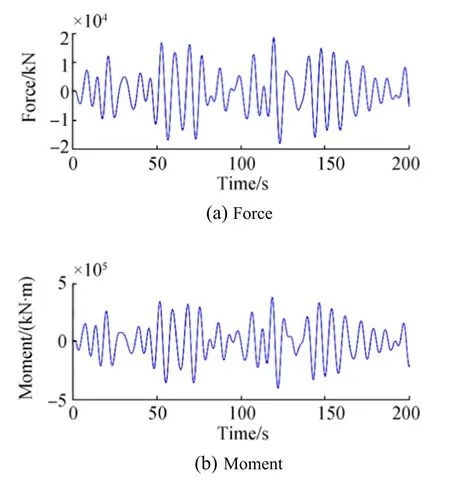
Fig.3 Forces and moments generated by random waves of SSN 4.a Force.b Moment

where P(t)is the pitch motion in(°).

Motion sickness incidence(MSI)is used as an evaluation term for the passengers and is defined as the percentage of people getting sick when experiencing vertical acceleration after 2 h of motion.

The rise in MSI when increasing the speed of the ship has been always an issue facing the ferries development by imposing a limitation on their speed operating range.The MSI can be calculated using the following formula(O’Hanlon and MacCawley 1975):

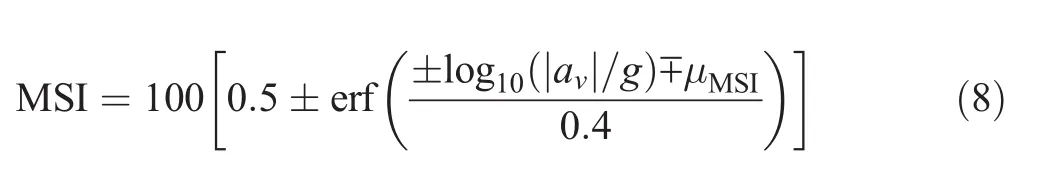
where erf is the error function,|av|is the vertical acceleration measured at the worst place on the ship,and μMSIis given by the folowing expression:

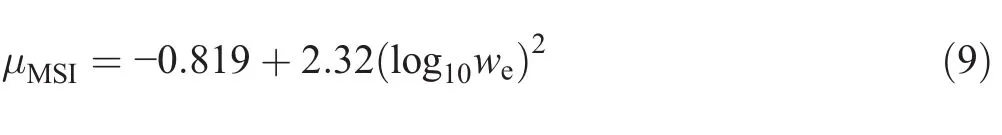
where ωeis the frequency of wave encounter and it is calculated for the head sea as follows:

By introducing the T-foil,the pitch motion and its acceleration are reduced as well as the MSI without needing to slow down the ship.

3 Model-Free Control

Model-free control(MFC)is a very recent approach to nonlinear control that was introduced by(Fliess and Join 2009).This approach consists on designing a control law while no mathematical model of the system dynamics is needed.The MFC is based on a continuously updated ultra-local model only with the knowledge of the input-output of the system.The input-output behavior is approximately governed within its operating range by a partially known or totally unknown finite-dimensional differential equation:

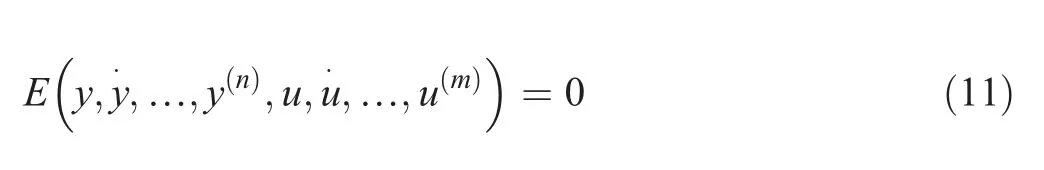
Equation(11)is replaced by an ultra-local model valid within a short-time interval as follows:

α is a nonphysical constant that is determined by the control designer to ensure a certain control performance.

The differentiation order v is also a designer choice and it is generally chosen to be 1 or 2 in the model-free control systems literature(Fliess et al.2011;Fliess and Join 2013).

F captures the unknown dynamics and the system behavior under perturbations and/or parameter uncertainties from the input-output signals.The numerical value of F must be updated at each sample time since Eq.(12)is valid only for a short time window.An approximation of the system dynamics is created based on the purely numerical ultra-local model that is used for the control law design.

For our application v was chosen to be equal to 2 and the ultra-local model becomes the following:

The numerical value of F is estimated based on the online parameter identification technique explained in the following section.

3.1 Numerical Estimation

First, the second derivative of the noisy signal y is estimated. This problem is chosen to be solved by Taylor/Maclaurin series based on algebraic differentiation scheme(Fliess et al.2008).

The third order approximation and Maclaurin times-series of the output signal y(t)around t=0 is presented as follows:

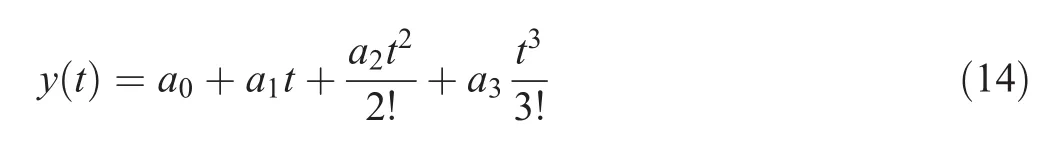
Applying the Laplace transformation to(14)the following equation is obtained:

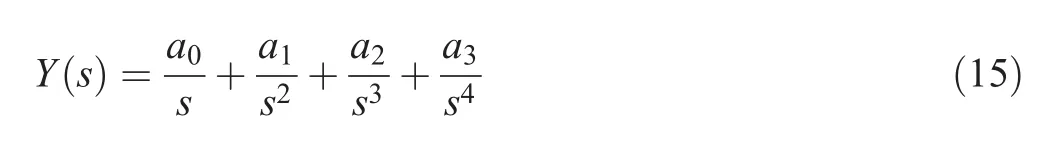
Then,by multiplying by s4:

This equation is differentiated once with respect to s to eliminate the constant a3and then multiplied by.Then,the equation was operated withto eliminate all nonneeded constants and remove the appearance of any positive powers of s that correspond to a differentiation operation in time domain.The resulting equation is the following:

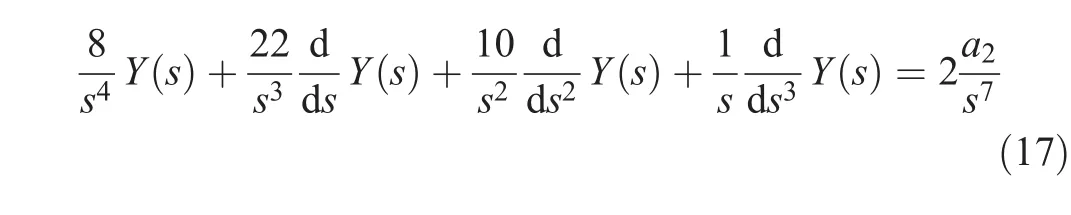
Now back to the time domain using the inverse transformation rules,

The well-known Cauchy repeated integral formula is also used:

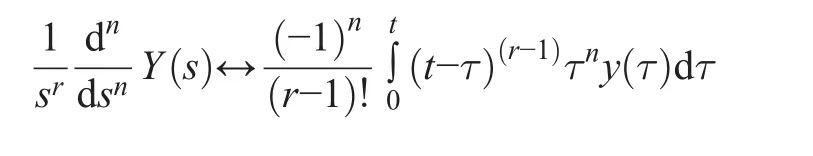
The estimate of the second derivative of output signal y is the following:

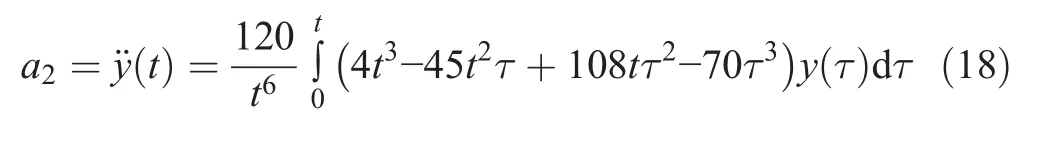
By changing the integration borders to a small fixed length window T,the final expression for the algebraic estimator of the piecewise constant function F is obtained:

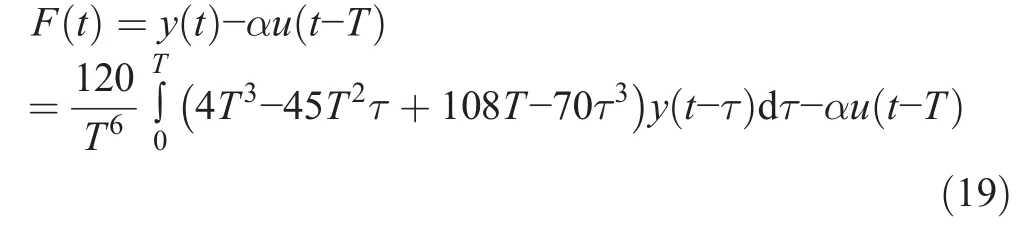
3.2 Controller Design

Based on the previously estimated numerical value of F,the control input u(t)can be calculated as a simple cancelation of the influence of the resultant disturbance and unknown dynamics termsplus a closed loop stabilizing term,

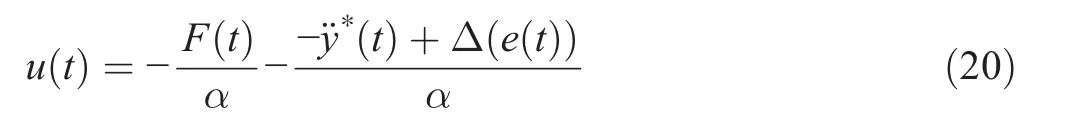
e=y-y∗is the output error.

Combining(13)and(20),

Δ(e(t))is an appropriate function which is selected such that asymptotic stability is ensured:

The term Δ(e(t))is chosen to be a PD control law.The control input of the feedback is expressed as the following:

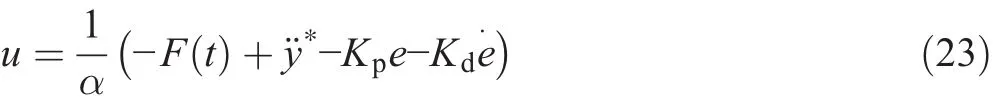
Kpand Kdrepresent the usual tuning proportional and derivative gains,respectively.

Equation(21)becomes a linear differential equation of the error.Hence,the selection of Kpand Kdis straightforward to ensure stable closed loop dynamics

The integral action of the classic controller exhibited a negative effect on the control performance therefore a PD controller was selected.

The resulting controller from Eq.(20)is an i-PD controller that consists of a PD controller augmented with an intelligent termthat contains all the structural information of the system dynamics to be canceled.The overall control law is composed of a cancelation of the influence of the resultant disturbance and unknown dynamics termsplus a closed loop PD controller term that ensures stable closed loop dynamics.

This control scheme is summarized in Fig.4.

4 Numerical Experiments

Numerical tests were performed on the fast ferry equipped with a T-foil controlled by the designed i-PD controller.White Gaussian noise was added to the output as sensor noise to obtain a complete model of the controlled system in its operational environment.

To show up the superiority of the proposed controller,a comparison of the results using a classic PD controller was performed.The parameters of the classic PD controller Kpand Kdwere tuned to obtain an optimal desired performance and they are listed in Table 2.

The identification of the piecewise function F with the fast estimation was performed through a time window of T=0.2 s.The gains of the i-PD controller,listed in Table 2,were directly selected to ensure the closed loop stability,and the constant α was tuned by trial and error to attained a good closed-loop performance.

The results of testing the fast ferry at 40 kn in head sea and a predominant frequency of SSN4 are presented in Figs.5,6,7,and 8.

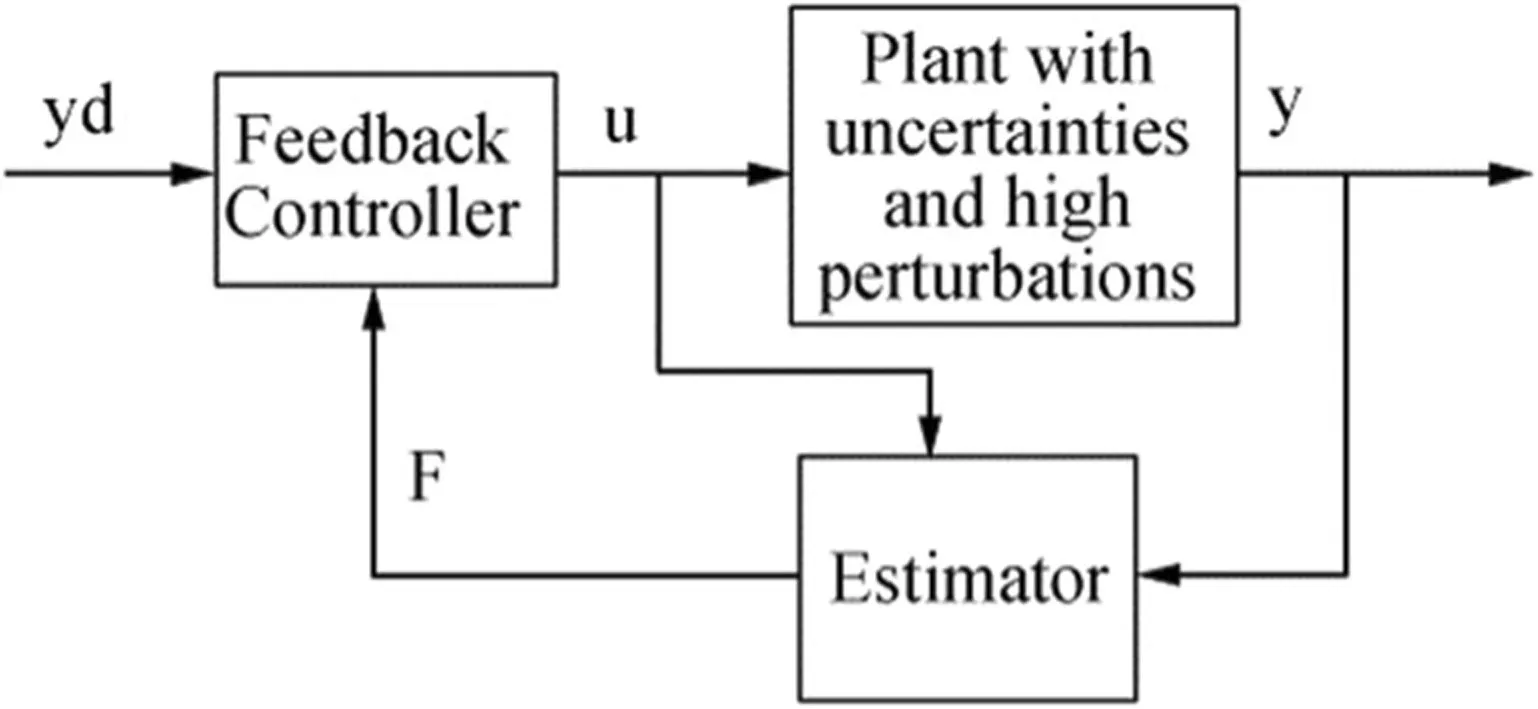
Fig.4 Control scheme of model-free control

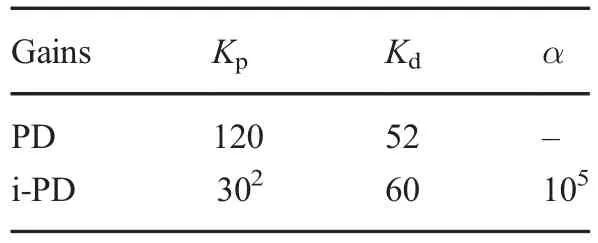
Table 2 Controller parameters

Fig.5 Pitch motion response without controller and with PD and i-PD controllers

For instance,Fig.5 shows the pitch motion signal without controlling and the same motion when controlling the T-foil once by the PD controller and then by the i-PD controller.It can be clearly seen that with the classic PD controller,there is a significant attenuation in the pitch motion and its vertical acceleration that is shown in Fig.6.However,the i-PD controller performs better than the classic PD controller with a mean WVA of 0.28 m/s for the i-PD versus 0.32 m/s for the PD controller.

Indeed,by using the i-PD controller,the reduction in WVA is translated into a reduction in the MSI as presented in Fig.7.Therefore,the passengers suffer much less from seasickness than when using the PD controller.This corresponds to a total reduction in MSI of 89.3%for the i-PD and only 85.4%for the PD controller.This result is highly positive for the comfort of passengers and the rise in the operational capabilities of the ship.The added intelligent termto the PD structure counteracted the effect of random wave’s disturbances.Due to the ability to constantly re-identify the local model at each sample time,the i-PD controller was able to perform better and improve the dynamic behavior and the rejection of the perturbation effects.Thus,the i-PD controller has more robustness against disturbances through random wave perturbations.Also,as shown in Fig.8,the T-foil follows the control law avoiding saturation and can well handle the control effort limits.

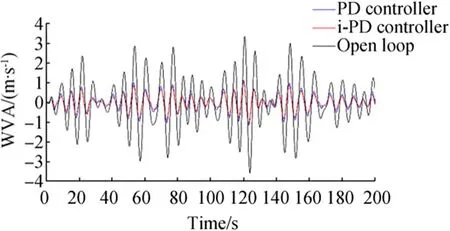
Fig.6 WVA response without controller and with PD and i-PD controllers

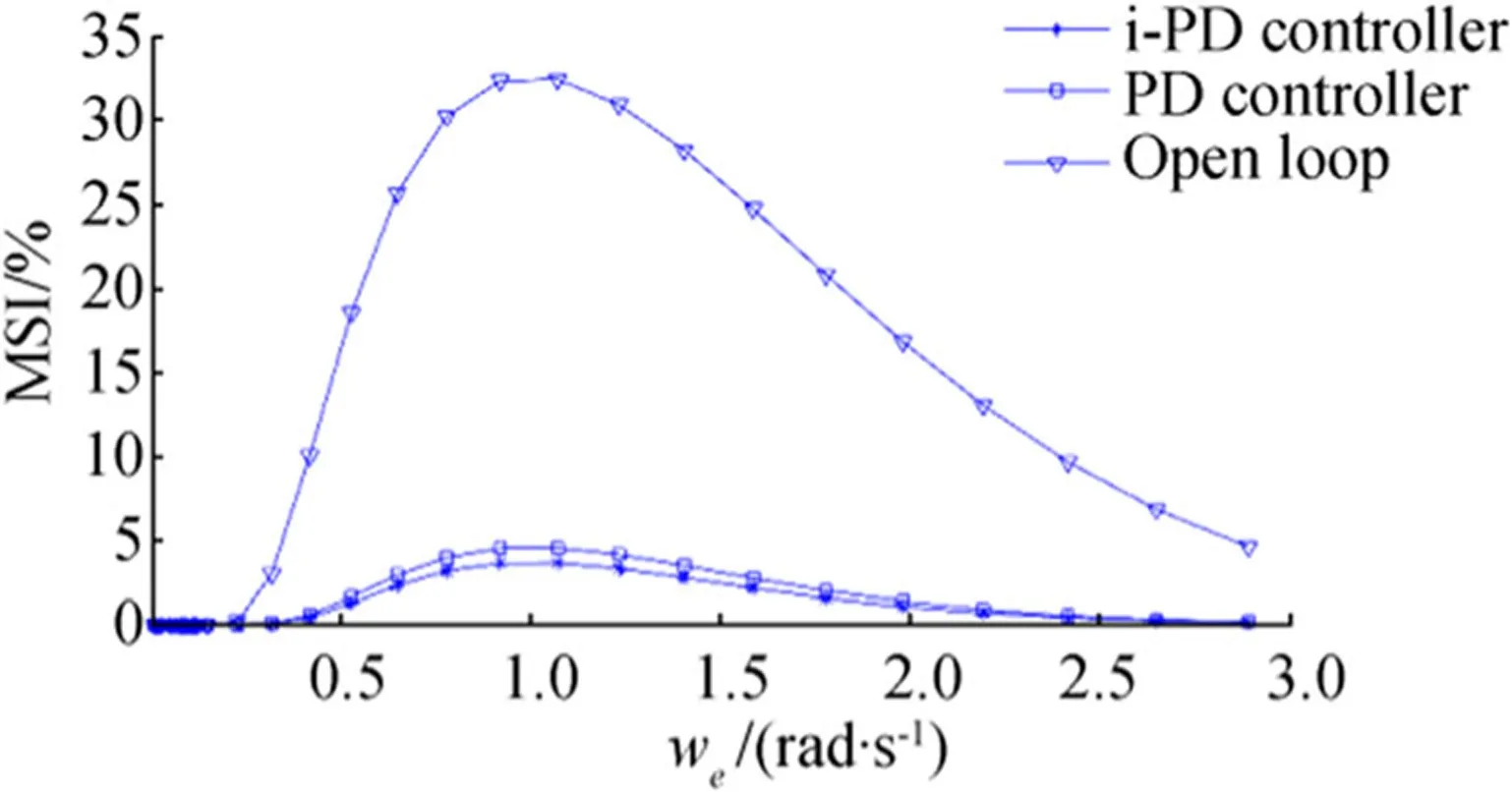
Fig.7 MSI percentages at 40 kn and SSN4

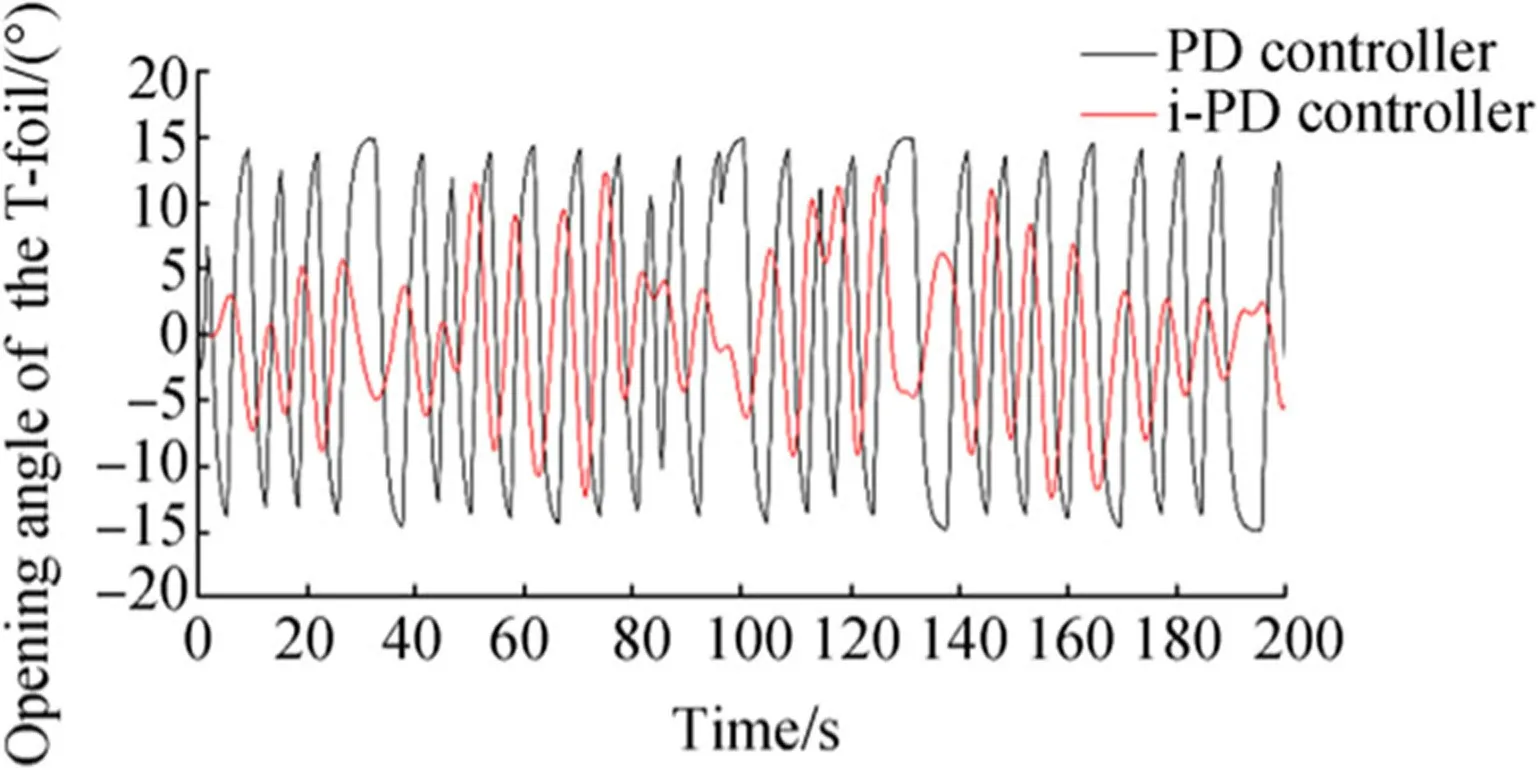
Fig.8 Opening angle of the T-foil for the PD and i-PD controllers

4.1 Robustness Study with Changing Parameters

As ship parameters are highly dependent on sea wave frequency and motion amplitude,a robustness test to changing parameters was performed.Model parameters were changed up to 30%without retuning the gains of both controllers,and the results are presented in Figs.9 and 10.The figures show the degradation in the performances of the classic PD controller,whereas the performances of the i-PD controller remain good.

The PD controller does not adapt to changes of the plant while the i-PD controller is shows sufficient control capacity that does not rely on model parameters.

Table 3 summarizes the obtained mean WVA and MSI percentages.According to Table 3,the performances of the PD controller dropped to 78.71%of MSI reduction whereas the i-PD controller reached a reduction in MSI of 92.88%.

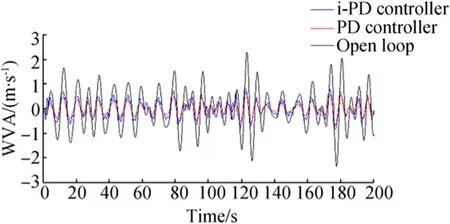
Fig.9 WVA responses after changing parameters

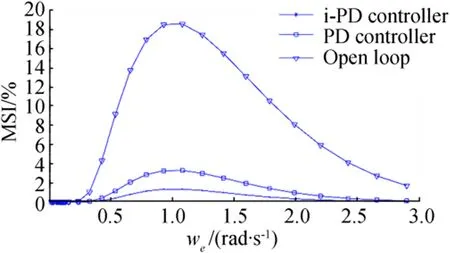
Fig.10 MSI responses after changing parameters

Here,the superiority of i-PD controllers over PD controllers is further confirmed.A good reduction is ensured without the need to adjust the gains of the controller,although model parameters changed.Hence,the intelligent controller has model-free characteristics and it is stronger against parameter variations and disturbances.

4.2 Robustness Study with Changing Speed

Both controllers were then tested at three different operating speeds(20,30,and 40 kn).This time the PD controller was tested twice.First,with maintaining the gains of the PD controller constant and the second with retuning the gains at each nominal plant related to each speed while the gains of the i-PD controller were maintained fixed.Table 4 resumes the obtained MSI for the three controllers at three different working speeds.

According to Table 4,the obtained MSI results with the tuned PD controller are better than those obtained with the non-tuned PD controller,which is an expected result.In the gain scheduling scheme,the controller is optimally tuned for the corresponding operating points.However,even by retuning the PD controller at different speeds,the obtained results using the i-PD controller are still better.

This result is because the i-PD controller is designed to be robust by ensuring the PD controller performances.In addition,the intelligent term permits to acquire the updated information on the system behavior to better counteract the effect of the disturbances.

Table 3 WVA and MSI percentages obtained with model changed parameters

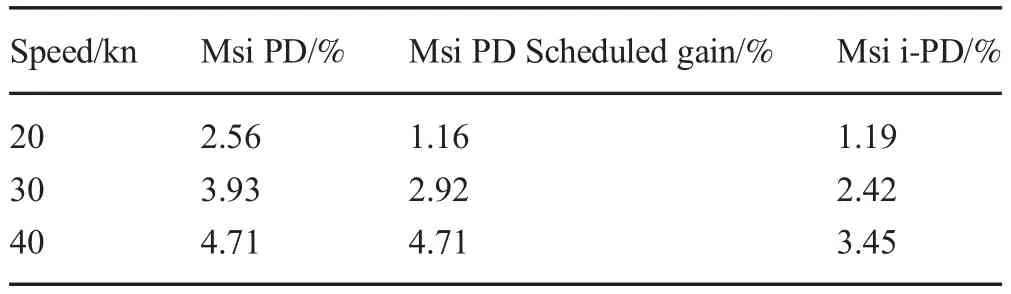
Table 4 MSI percentages at 20,30,and 40 kn

5 Conclusion

This work discusses the reduction of the vertical motions inducedby random waves of a fast ferry and the improvement of the comfort of its passengers using a controlled submerged T-foil.An intelligent PD controller based on model-free control approach is designed to properly move the T-foil.The performances of the i-PD controller were compared to those of a classic PD controller when experiencing random sea waves.The effectiveness and robustness towards disturbances and model uncertainties of the designed controller were then shown via several different simulations.First,the i-PD controller showed a straightforward method for gain tuning compared to the PD controllers which tuning is very dependent on the model.Secondly,the results showed that the i-PD controller exhibited a good disturbances rejection better than the classic controller.Also,unlike the PD controller,the i-PD controller demonstrates the capacity to handle the change in system parameters. Furthermore, the two controllers were tested at different operating speeds,and the i-PD controller highlighted its superiority over the PD controller.This work presents a convincing application of the new model-free control in marine technology,and this is a field in which model based control is especially difficult to develop.It serves as a good contribution for ship vertical motion attenuation and improving the comfort of passengers.Meanwhile,this research provides a baseline for further studies with an enlarged operational range.