Internal Resonances for the Heave Roll and Pitch Modes of a Spar Platform Considering Wave and Vortex Exciting Loads in Heave Main Resonance

Wei Li·Yougang Tang·Bin Wang·Yan Li

Abstract

Keywords Spar platform . 3-DOF nonlinearequations .Multiplescales .Sub-harmonic response .Jump phenomenon.Sensitivity analysis

1 Introduction

Previously,the parametric or internal resonance has been used to investigate the pitch-roll coupled motion for ships.Froude(1863)noted an unstable roll motion when the ratio of the natural frequency of roll and pitch was approximately 2:1.Nayfeh et al.(1973-1988,2011),Mook et al.(1974),conducted numerous works on the coupled pitch-roll motion for ships with nonlinear dynamics.Sayed and Hamed(2011)studied a two DOF system with quadratic coupling under parametric and harmonic excitations for a ship.The multiple-scale method was used to analyze the response of a nonlinear system and the results were compared with the available published work.

Haslum and Faltinsen(1999)studied the coupled Mathieu instability for heave and pitch without damping.They demonstrated that the nonlinearity of the spar platform was due to the influence of the heave motions on the pitch restoring.Rho et al.(2003)studied the mooring effects on the stability of the spar platform.The results demonstrated that the mooring system has only a small effect on preventing nonlinear motion.Koo et al.(2004)discussed the Mathieu instability of a spar platform with damping effects,mooring,and risers and found that pitch damping significantly suppressed the instability.The results showed that the buoyancy can pitch natural period plays an important role in the Mathieu instability.Rho et al.(2005)investigated the vertical motion stability of a spar platform based on the coupled heave-pitch Mathieu equation with damping.The numerical results were confirmed by the model tests.A large heave motion makes the GM negative,exciting the unstable pitch motion.Neves et al.(2008)studied the occurrence of the Mathieu instabilities of a vertical cylinder for the heave,roll,and pitch mode in regular waves.They used different mooring systems to observe the nonlinear resonance and stated that the dynamic pressure field was a reason for the parametric resonance aside from the vertically driven pendulum phenomenon.

Zhao et al.(2009,2010)studied the internal resonance characteristic of a classic spar platform in heave and pitch mode with nonlinear dynamic theory.The results demonstrated the energy saturation phenomenon in the heave mode when the heave amplitude arrives at a certain value.Extra energy was transferred from the heave to pitch mode,thereby resulting in a large amplitude of the pitch motion(Zhao 2010).Shen and Tang(2011)studied the nonlinear stochastic motion of a truss spar in the heave and pitch mode.A large amplitude of the pitch motion was excited when the characteristic frequency of the stochastic wave was close to the natural heave frequency.Liu et al.(2014a,b)studied the heave-pitch internal resonance response of a spar platform and drew a stability diagram in regular waves.Yang and Xu(2015)proposed the pitch stability diagram in irregular waves of a spar platform.The unstable property was determined by analytical method and numerical simulation.

Li et al.(2017a,b)studied the nonlinear internal resonance of a spar platform in the heave,roll,and pitch mode in the heave main resonance considering the vortex-induced motion.The results showed that the energy infiltration occurred in the heave,roll,and pitch mode with internal resonance.The energy infiltration was closely connected with the damping and initial condition.The response of roll was more complicated with the influence of the vortex-excited force.In addition,Li et al.(2017a,b)studied the nonlinear internal resonance in roll resonance.The results showed two nonlinear response cases with changing vortex exciting loads.Some sensitivity analysis was made to determine the effects of the damping and detuning factor.

According to the earlier motion equations,we obtained herein two possible first-order perturbation solutions:linear and nonlinear solutions.We determined the boundary conditions of the real root for the nonlinear solutions.We made some sensitivity analyses to test the influence of different parameters,such as amplitude of the wave excitation force,damping,and internal detuning factor.The general character of the solutions changing with the parameters was obtained.

2 First-Order Perturbation Solution of the 3-DOF Coupled Equation

Li et al.(2017a,b)considered the motion of a spar platform with three DOF(heave,roll,and pitch)when second-order nonlinear couplings were included in the motion equations.The equations are presented as follows:

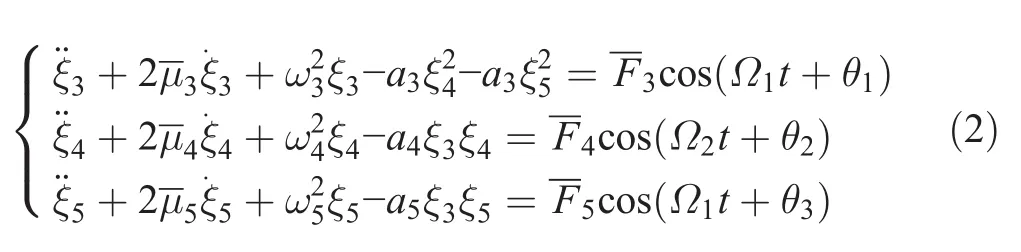
where m is the mass of spar;m33is the added mass of spar;I is the inertia moment;I44and I55are the added moment of inertia for roll and pitch,respectively;∇is the spar displacement;Biis the radiation damping;F3and F5are the amplitudes of the heave and pitch wave excitation loads,respectively;F4is the amplitude of the vortex excitation loads;Ω1is the frequency of the incident wave;and Ω2is the frequency of the vortex induced force.

After including the second-order nonlinear terms,the motion equations can be written as follows:

where

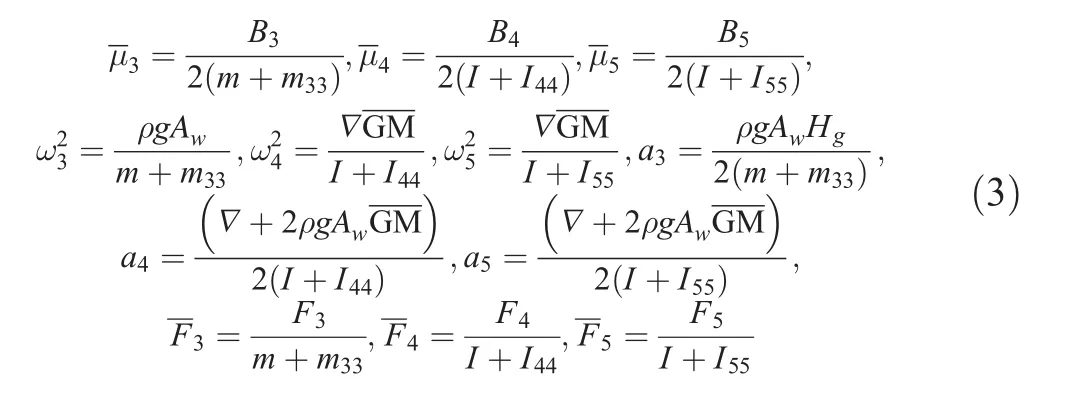
We used the multi-scale method to determine the first-order approximate solutions of Eq.(2).The motion equations were simplified with new dependent variables to eliminate a3,a4,and a5from Eq.(2).

where

For convenience,ε was considered to be a measure of the response amplitude.We considered it to be small compared with unitywas defined as:= εμi;i=3;4;5.

According to the multi-scale method,different time scales were introduced:

The incident wave frequency herein was close to the heave natural frequency.The nearness of Ω1to ω3was expressed by the detuning parameter σ1,such that:

The nearness of ω3to 2ω4and 2ω5was expressed by the detuning parameters σ2and σ3:

To make the heave forced term come together with damping term in the same first-order perturbation equation when Ω1≈ ω3,we assumed that,

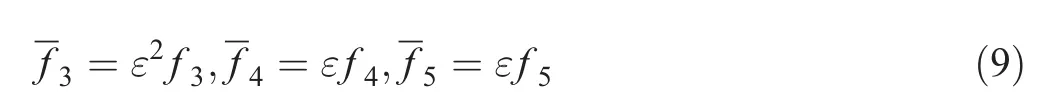
The motion equations are written as follows:

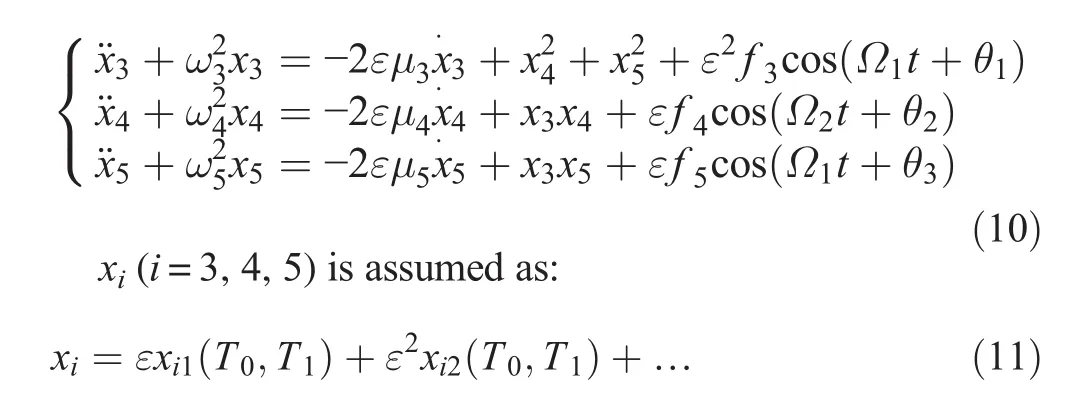
The time derivatives are transformed according to

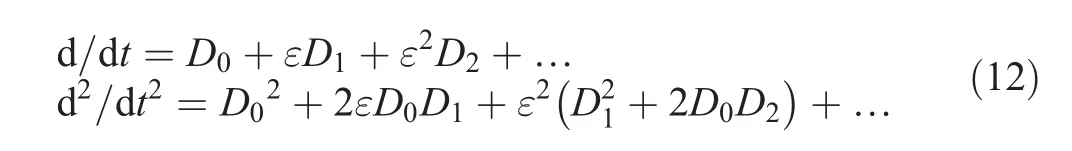
where Dn= ∂/∂Tn.

Substituting Eq.(11)into Eq.(10)and equating the coefficients of equal powers of ε,we obtain:

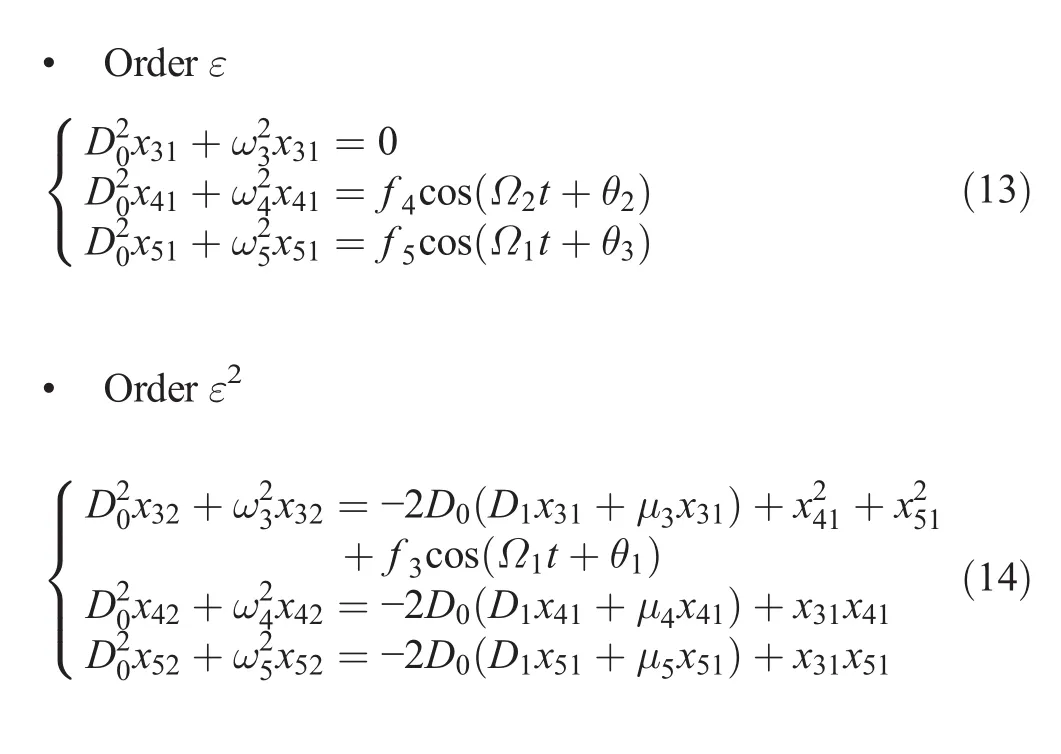
The first-order approximate solutions to Eq.(10)can be expressed as follows:

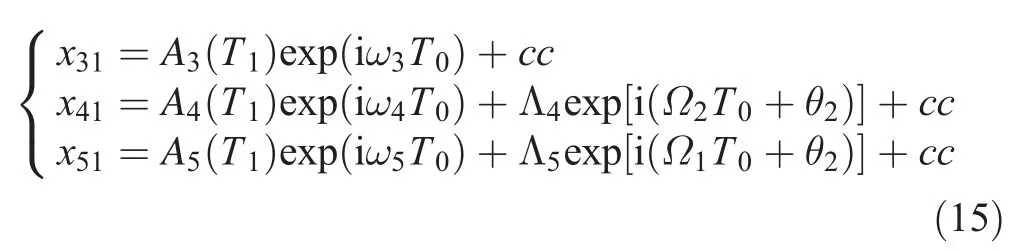
Substituting Eq.(15)into Eq.(14),we obtain:

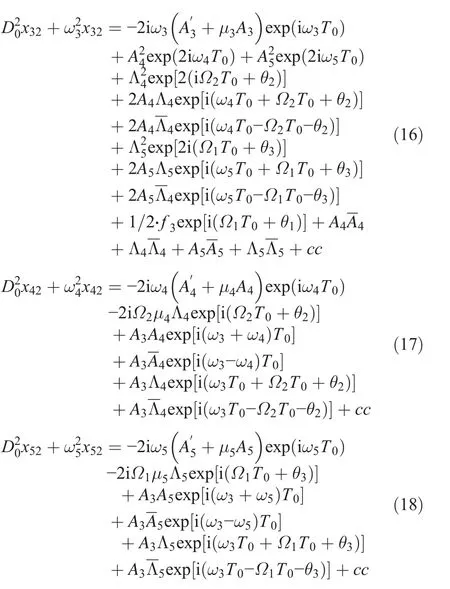
Substituting Eqs.(7)and(8)into Eqs.(16)-(18),the solvability conditions can be written as:

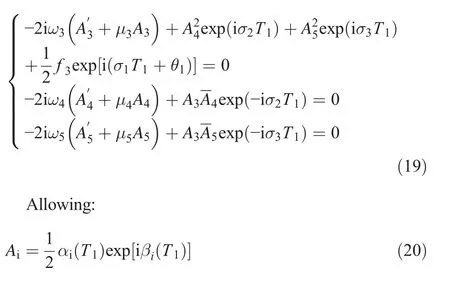
where αi(T1)and βi(T1)are real.The following is defined as:

We obtained the following equations by substituting Eqs.(20)and(21)into Eq.(19):

The steady-state response is given by==0.We have two possibilities:Case(a) α4and α5are zero,and α3is a non-zero and Case(b)α3,α4,and α5are non-zero.

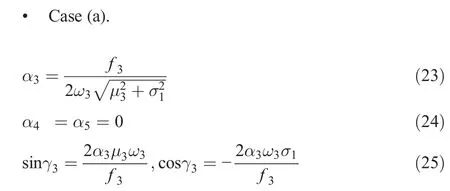
The first-order perturbation solution for Eq.(10)is written as:

which is essentially the linear solution.This constant solution corresponds to a simple-harmonic response with the same period as the excitation in heave,roll,and pitch.

We observe that Eq.(28)is invalid when μ4≠ μ5.Here,either α4or α5is zero.Assuming α5to be zero,Eq.(30)can be written as follows:

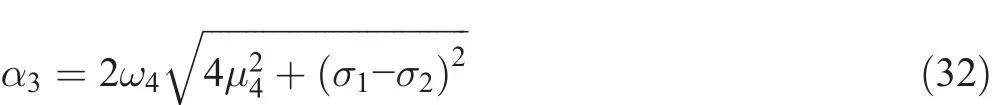
The first-order perturbation solution for Eq.(10)is expressed as:

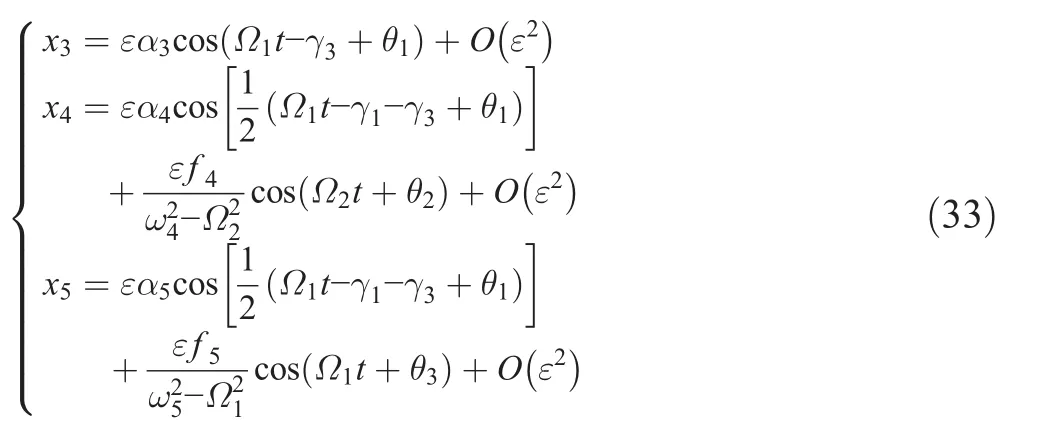
Finally,the heave,roll,and pitch coupling motion response are expressed as follows when the incident wave frequency is close to the heave natural frequency:

Equation(28)shows an interesting feature of the heave mode,although the heave mode is being driven by a simple-harmonic excitation with the same period of the wave,the amplitude of the heave mode α3is independent of its exciting force f3and heave damping μ3.Eq.(29)shows that the total energy of the roll and pitch mode is constant in a specific sea condition.The half subharmonic responses driven by the wave excitation occur in the roll and pitch mode,except for the simple-harmonic response with the same frequency as the wave excitation and vortex-induced excitation.α4and α5are only dependent on the exciting force,f3,in the heave mode,which is considerably different from case(a).

Next,we determine when the roots of Eq.(29)are real with:

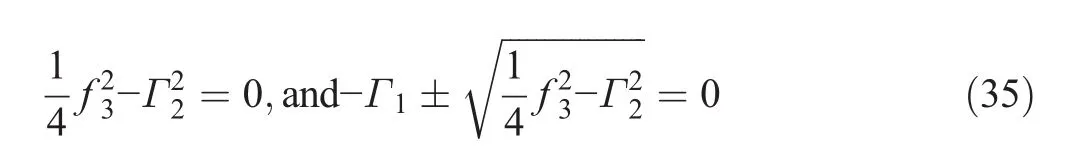
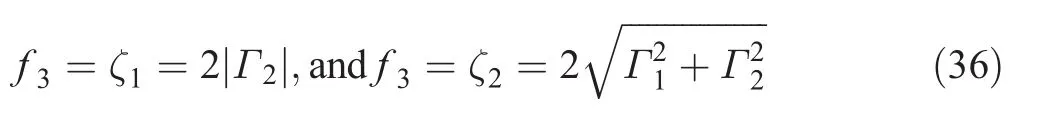
ζ2must be greater than ζ1.A real solution to Eq.(29)can only be obtained if f3＞ ζ1=2|Γ2|.When f3＜ ζ1,the response must be obtained from the linear solution Eq.(26).When f3＞ζ1,two possibilities are considered:Γ1＜0 and Γ1＞0.

When Γ1＜ 0,at most,one real solution exists only if f3＞ζ2.Consequently,when f3＜ζ2,the response must be given by the linear solution.Moreover,when f3＞ζ2,the response is one of two possibilities.

When Γ1＞ 0,one real solution exists if f3＞ζ2.Two real solutions exist if ζ1＜ f3≤ ζ2.Consequently,when f3＜ζ1,the response must be obtained from the linear solution.When ζ1＜ f3≤ ζ2,the response is one of the three possibilities,whereas when f3＞ζ2,the response is one of the two possibilities.

We need to determine the stability of the aforementioned solutions to verify which of them describe a response of the spar platform.

We define two critical values of f3as follows:

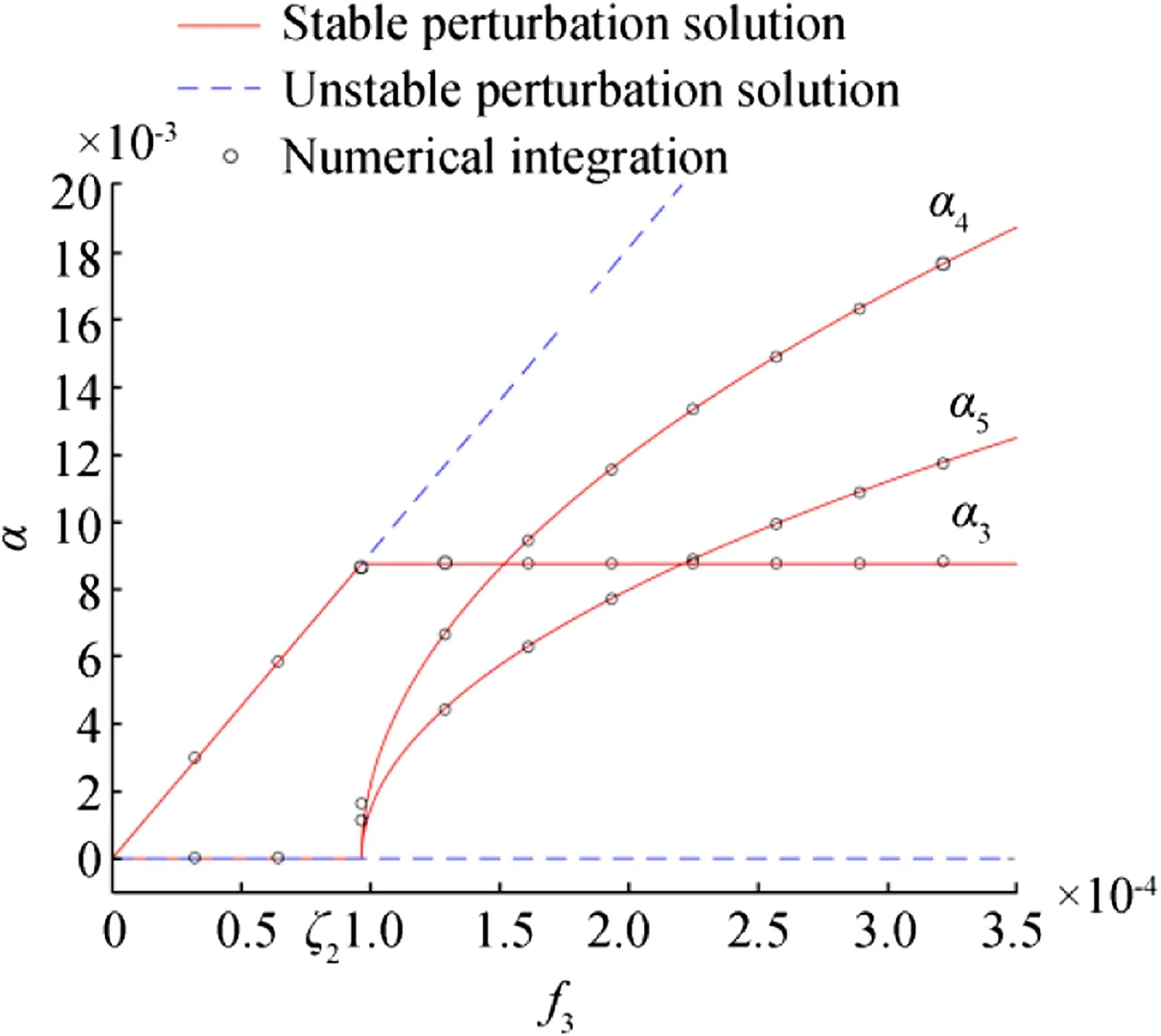
Fig.1 Heave,roll,and pitch amplitude with wave excited force f3when σ1=0 and Ω1= ω3

3 Numerical Results and Discussion

We chose the parameters in Hong et al.(2005)to illustrate the analytic solutions. The results were compared with the numerical simulation. Lyapunov stability theory was used to analyze the stability of the analytic results.Table 1 shows the parameters of the spar platform.

We obtain the following by calculating the dimensionless coefficient in Eq.(2):

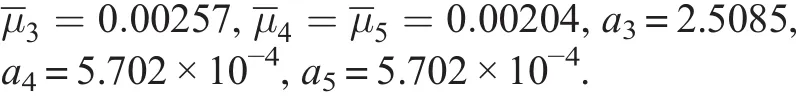
The natural frequencies for the heave,roll,and pitch mode are:

ω3=0.2144rad/s,ω4=0.1072rad/s,

ω5=0.1072rad/s,respectively.

The amplitude of the heave,roll,and pitch(α3,α4,α5)are illustrated as functions of the amplitude of the wave excitation,f3,detuning parameters(σ1,σ2,σ3),and damping coefficients(μ3,μ4,μ5).The continuous lines in all the figuresherein represent stable solutions.The dashed lines represent unstable solutions,and the circle dot lines represent numerical integration.

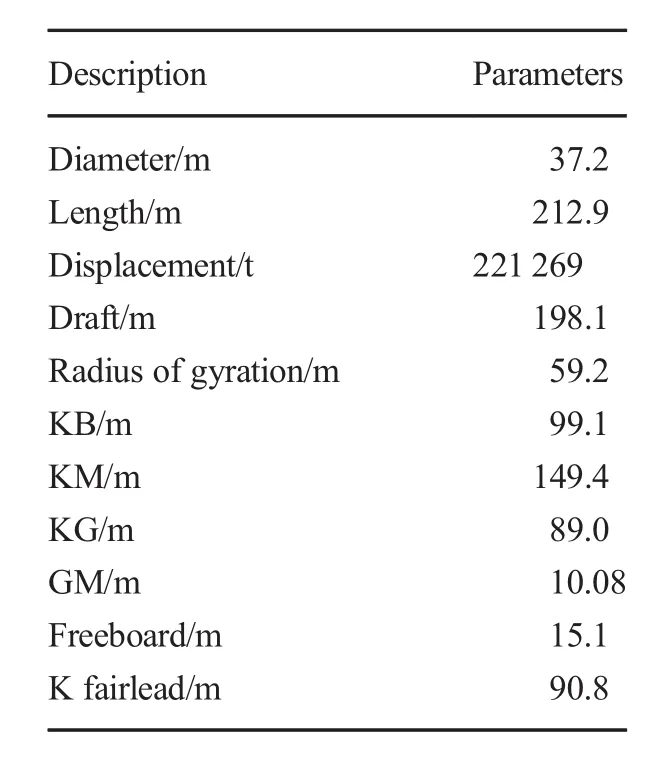
Table 1 Characteristic parameters of the spar platform

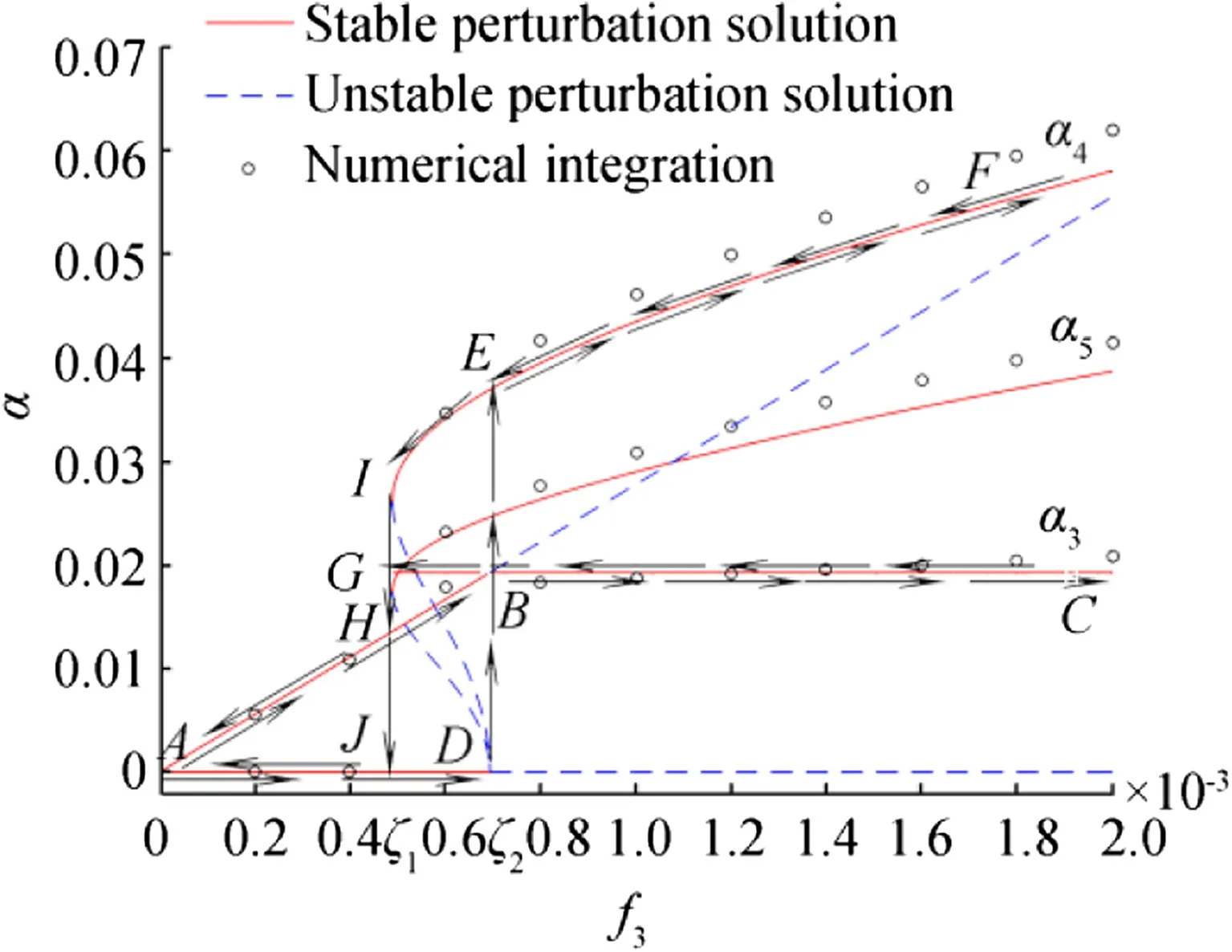
Fig.2 Heave,roll,and pitch amplitude with excitation f3when σ1=0.08 and Ω1≈ ω3

Fig.3 Excitation-response curves for various damping values when Ω1≈ω3

The amplitude of heave(α3),roll(α4),and pitch(α5)are plotted in Figs.1 and 2 as a function of the amplitude of the excitation,f3.The incident wave frequency is equal to the heave natural frequency(σ1=0)in Fig.1 and approximately equal to the heave natural frequency in Fig.2(σ1=0.08).Only one stable solution in all the regions can be found in Fig. 1. However, unlike Fig. 1, different solutions are available in different regions. Two stable solutions can be used when ζ1＜f3＜ζ2,whereas only one stable solution can be used in the other regions.Figure 2 shows a jump phenomenon associated with the varying f3.As f3increases from zero,α3follows a solid line from A to B,and α4remains zero from A to D until f3equals ζ2.α3remains constant α*3from B to C as f3increases beyond ζ2.α4jumps from D to E.α4increase along the curve from E to F as f3continuously increases.α3remains constant from C to G as f3decreases from a value greater than ζ2.α4follows the curve from F to I until f3equals ζ1.α3drops from G to H,and α4drops from I to J,as f3continues to decrease.α3decreases along the curve from H to A as f3decreases from ζ1to zero.α4decreases from J to A.

Fig.4 Heave,roll,and pitch frequency-response curves when σ2=0 and Ω1≈ω3

Figures 1 and 2 show that the perturbation solution is validated by the numerical integration solution.They also clearly present a saturation phenomenon.The heave response α3was independent of the wave excitation f3when f3＞ζ2.The rollα4and pitch α5rapidly increased with the increasing wave excitation.α3increased with f3,whereas α4and α5remained zero when f3＜ ζ2.This was the solution to the linearized problem.The linear growth heave amplitude α3did not continuously increase but remained constant,when f3=ζ2.The increase in f3only produced an increase in the amplitude of the roll α4and pitch α5.In other words,the heave energy was saturated,and the heave mode could not hold more energy.The extra energy transferred from the heave mode to the roll and pitch can cause a large amplitude for the roll and pitch.The differences between the amplitude for the roll α4and pitch α5were caused by the initial condition.

Based on Fig.2,we plotted α3,α4,and α5as a function of f3(Fig.3)with different values of damping to analyze the damping effect.Combined with Eq.(28),we found that the amplitude of the heave motion α3with an internal resonance was independent from heave damping μ3.In Fig.3,the heave amplitude α3remained the same when the heave damping μ3increased from 0.0257to0.0411,and μ4and μ5remained as0.0204.In contrast,the amplitude of the roll and pitch decreased.μ3remained 0.0257 when μ4and μ5increased from 0.0204 to 0.0408.The amplitude of the heave motionα3increased,whereas the amplitude of the roll α4and the pitch α5decreased.

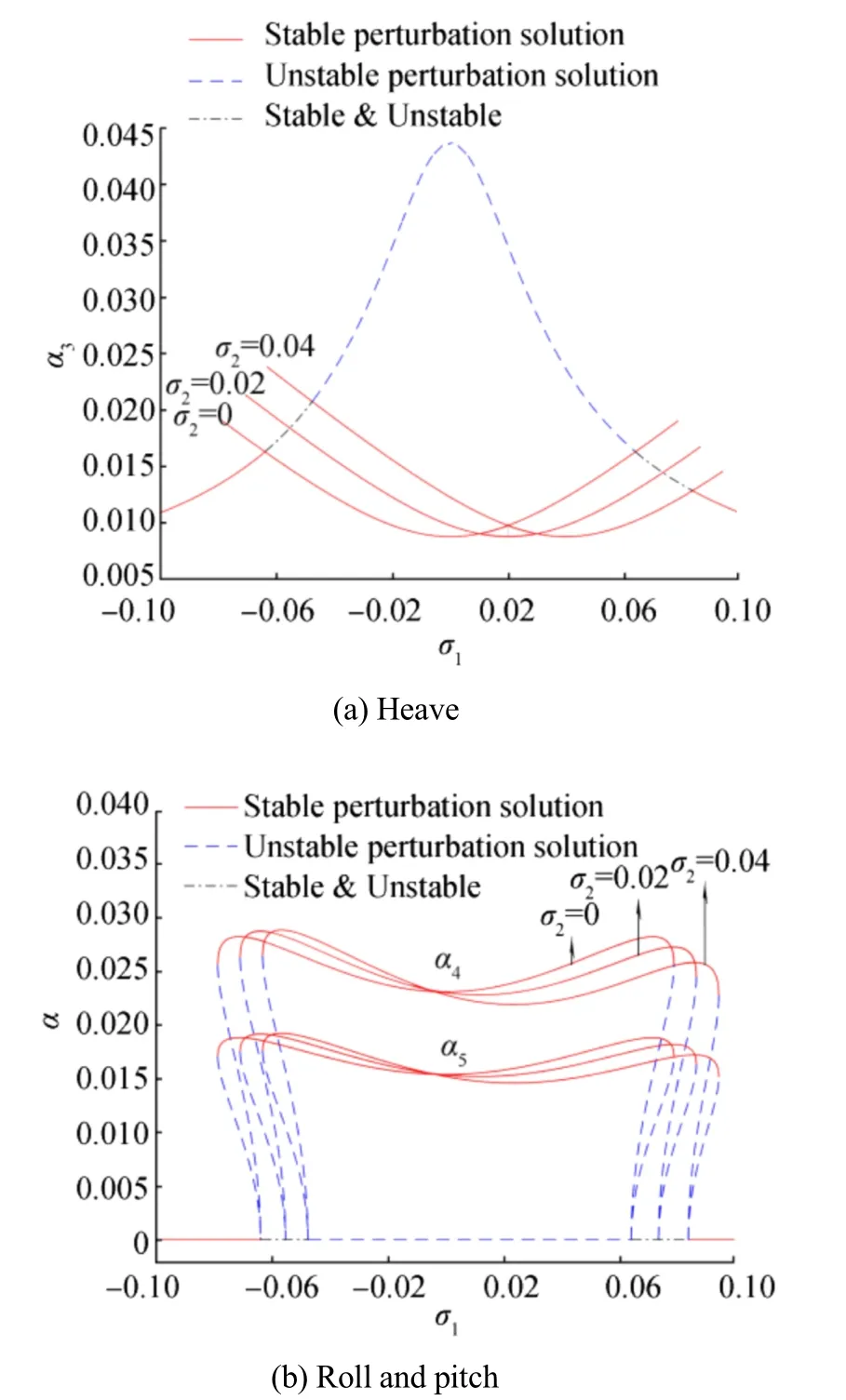
Fig.5 Frequency-response curves for various values of σ2when Ω1≈ω3

Figure 3 shows the influence of damping on the solution,indicating that the multiple-solution region depended on damping coefficients μ3, μ4,and μ5.In other words,the damping can restrain the nonlinear responses.Meanwhile,the region between ς1and ς2decreased as the damping increased.The multiple-solution region disappeared when the damping further increased.As a result,the roll and pitch response did not exhibit two stable motions and the jump phenomenon.We conclude from Fig.3 that the mechanism of the energy transfer from heave to roll and pitch becomes more difficult with the increase in damping.

In Fig.4,α3,α4,andα5are plotted as functions of σ1when σ2=0.Only one stable solution is found in the center region(-0.064＜σ1＜0.064),which corresponds to Fig.1.The first order perturbation solutions corresponded with the numerical results.In the-0.079＜σ1＜-0.064 and 0.064＜σ1＜0.079 region,two stable solutions correspond to Fig.2.The jump phenomenon resulted from the multiple solutions to the equation and was indicated by the arrows with the incident wave frequency change.The motion response amplitude may suddenly change as the incident wave frequency varies.In other regions,the solutions corresponded to the linearized problem.

Fig.6 Frequency-response curves for various damping values when Ω1≈ω3

The effect of the internal detuning parameter,σ2,was shown in the frequency-response curves in Fig.5 based on Fig.4.We note that the multiple-solution region changed for various values of σ2.For a given σ1(e.g., σ1=-0.06),the linear solution may be both a stable and an unstable solution.

Figure 6a, b and c shows the amplitude of the heave α3,roll α4,and pitch α5responses,respectively,with the change of the detuning parameter σ1for different damping values.The multiple-solution region depends on the damping.We note that at μ3=0.0411 and μ4= μ5=0.0326,only one stable solution can be found in all the regions.Hence,the jump phenomenon disappears with increasing damping.

4 Conclusions

The nonlinear coupled heave-roll-pitch internal resonance of a spar platform was studied herein in heave main resonance using an analytic method and a numerical calculation.The results are summarized as follows:

1)The coupled nonlinear internal resonance occurred in the heave resonant waves when the ratio of the heave,roll,and pitch frequencies was 2:1:1.The heave mode became unstable,causing a large amplitude of the half subharmonic responses in the pitch and roll mode.

2)A saturation phenomenon occurred in the heave mode when the spar platform exhibited internal resonance.The amplitude of the heave mode maintained a constant value with the increased amplitude of the heave wave force.The energy imported in the heave mode transferred to the pitch and roll mode.

3)The jump phenomenon was produced by varying the wave force.The motion amplitude of the spar platform in these regions suddenly changed,which harmed the riser and mooring systems.

4)Achieving the saturated value became difficult for the heave mode as the damping increased.Meanwhile,the multiplesolution region decreased as the damping increased.The multiple-solution region disappeared when the damping further increased. The roll and pitch response did not exhibit two stable motions and the jump phenomenon.