关于Lagrange插值公式教学的体会

陈 浩 王小丽

（1.重庆师范大学 数学科学学院 重庆 401331；2.重庆师范大学 地理与旅游学院 重庆 401331）

在数值分析的教学中，Lagrange插值类问题是一个难点. 数值分析教材广泛认为，Lagrange插值公式形式优美但其数值实现有一定的不足. 笔者认为，通过引入Lagrange插值公式的一种质心表示形式，可以克服其数值实现的困难. 同时，这不仅给学生们提供了解决插值问题的一类新思路，提高了学习效率，也提高了学生的认识，是值得尝试的.

设(xj,yj),j=0 ,…n为n+1个横坐标互不相同的插值节点. 令Pn为所有不超过n，次的多项式的集合. 则经典的插值问题为：求一多项式p∈Pn使其通过所有的插值节点，即：p(xj) =yj,j= 0 ,…n.该问题的解是存在唯一的且其解的Lagrange形式为[1]：

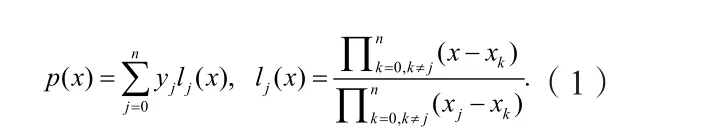
Lagrange插值公式的优点在于其形式优美且利于理论分析，其不足之处主要在其数值实现方面[2]，如：

1.计算p(x)需要Ο(n2)次加法和乘法运算；

2.增加一个新节点（xn+1,yn+1)需要重新计算；

3.数值不稳定性.

在数值实现方面，数值分析教材一般建议利用Newton插值公式与秦九韶算法结合[1]来实现，其计算p(x)仅需要Ο(n)次加法和乘法运算且增加新节点（xn+1,yn+1)不需要重复计算.

为得到Lagrange插值公式的等价形式，我们先将Lagrange插值基函数改写.令l(x)=(x-x0)(x-x1) (x-x),并定义质心权系数

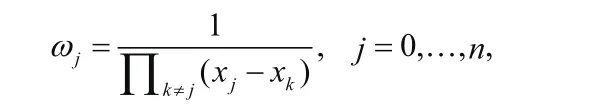
则有ωj=1/l'(xj)，因此Lagrange插值基函数lj可写为

从而，Lagrange插值多项式可改写为

式（2）即为Lagrange插值公式的等价变形之一，为使其更加对称优美，我们进一步将其改写. 由Lagrange插值余项定理[1]可知对常函数1插值所得插值多项式即为其本身，即

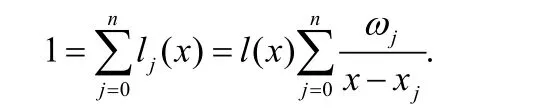
求出l(x)代入Lagrange插值多项式（2）式可得质心公式

此质心公式为Lagrange插值公式的等价形式，但其具有特殊且优美的对称性. 其计算p(x)需要Ο(n2)次加法和乘法运算且为了增加一个新节点（xn+1,yn+1)而更新权系数ωj仅需要Ο(n)次运算，同时其具备优良的稳定性[2].

Lagrange质心公式（3）相比Newton插值公式的好处之一是其避免了差商表的计算. 此外，Lagrange质心公式不依赖插值节点的排列顺序，而Newton插值公式中差商表的计算非常依赖插值节点的排序，尤其当n很大时很多排序会导致数值不稳定性.