关于插值型数值积分公式教学内容的探讨
陈 浩 王小丽
(1.重庆师范大学 数学科学学院 重庆 401331;2.重庆师范大学 地理与旅游学院 重庆 401331)
在数值分析的教学中,数值积分公式是很重要的内容,数值分析教材往往侧重于基于函数值的数值积分公式的分析,而对于基于函数值及其导数值的数值积分公式的探讨很少出现.Hermite插值涉及到被逼近函数的函数值及导数值,因此,利用插值型积分思想,启发学生思考Hermite插值是否可以用来解数值积分问题,并得出相关结论.这样做既可以将数值分析中插值与数值积分两大重要内容联系在一起,又可以培养学生分析问题、解决问题的能力,从而激发学生学习数值分析的兴趣,进而提高学生的认知与效率.本文将对此作一些初步的讨论.
设x0,… ,xn为区间[a,b]上n+1个互不相同的节点,且函数f(x)在此n+1个节点处的函数值f(xk)及导数值f'(xk)已知,则近似f(x)的2n+1次Hermite插值多项式为[1-2]
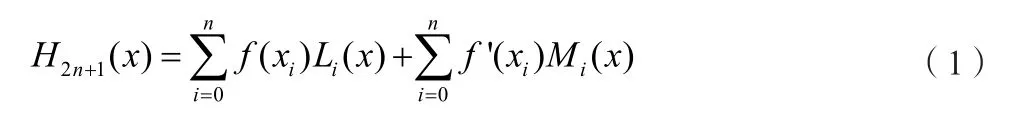
其中不超过2n+1次的多项式Lk(x),Mk(x)定义如下
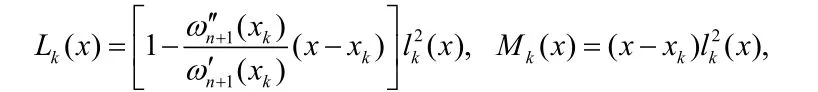
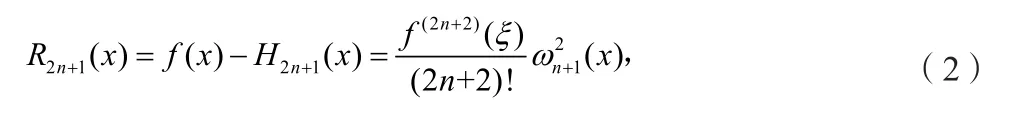
其中ξ∈[a,b].对(1)式在[a,b]上求积分可得基于Hermite插值的数值积分公式
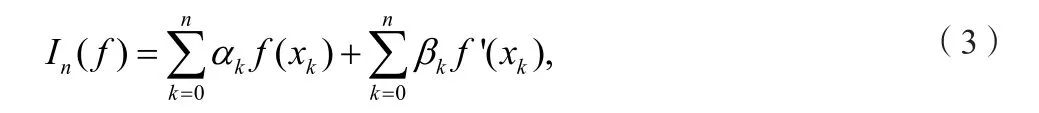

由(4)可知Hermite插值型积分公式(3)对不超过2n+1次的多项式是精确的,即此积分公式代数精度为2n+1阶.

表1 改进复合梯形公式计算例1的绝对误差
当n=1时,令x0=a,x1=b,计算可得α0=α1=(b-a)/2,则可得如下数值积分公式
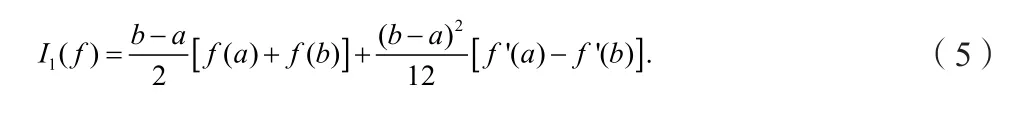
式(5)也称为改进的梯形公式. 若f(x) ∈C4([a,b]),则公式(5)的误差界为
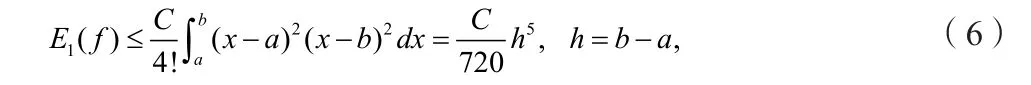
利用复合求积思想,将区间[a,b]分成m等分,求积节点xk=a+k(b-a) /m,在每个子区间上利用改进的梯形公式(5)并求和可得如下复合积分公式
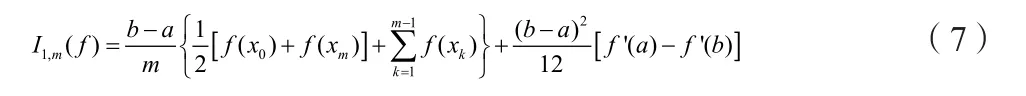
式(7)也称为改进的复合梯形公式, 其误差界为
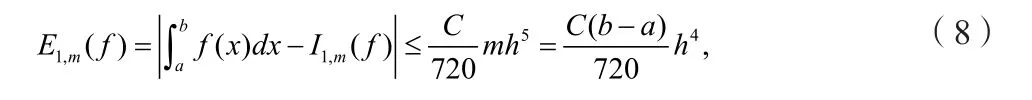
表1展示了当步长h减半(m倍增)时绝对误差及相邻误差比值:的变化情况
数据显示相邻误差比值趋近于16,即改进的复合梯形公式(7)数值收敛阶为4阶,进一步验证了(8)式中的理论误差界.

