积分在求和中的应用

（丹东市中医药学校 辽宁丹东 118000）

一、问题研究的背景

数学是一门应用性极强的学科， 积分学及其应用作为高等数学的一个分支， 在现实应用中的意义就更为显著。它不仅是一门重要的数学分支， 而且在物理学， 生物学， 经济学等领域及各种工程学科中有着极其重要的应用。

微积分是世界近代数学的重要内容， 也是近代数学进一步发展和拓展的重要基础。微积分思想的萌芽出现得比较早， 中国战国时代的《 庄子⋅ 天下》 篇中的" 一尺之棰， 日取其半， 万事不竭" ， 就蕴涵了无穷小的思想。古希腊数学家阿基米德在公元前三世纪运用杠杆原理推导出了球体的体积公式， 就包含了定积分的基本原理。之后， 帕斯卡在求曲边图形的面积时， 用到了“无穷小矩形”的思想并把无穷小概念引入数学， 为后来莱布尼茨的微积分的产生奠定了基础。

积分求和是伴随着微积分学一起发展起来的学科。 1686年， 莱布尼茨又发表了他的第一篇积分学论文《深奥的几何与不可分量及无限的分析》， 初步论述积分或求积问题与微分或切线问题的互逆关系。在这篇论文中， 积分号第一次出现在出版物上。积分求和有着深刻而生动的实际背景， 它从生产实践与科学技术中产生， 又成为现代科学技术中分析问题与解决问题的一个强有力的工具。积分求和成为了有自己的目标和方法的新的数学分支。

近年来， 国内外学者对积分求和做了许多研究， 无论是在深度还是广度方面都取得了重大发展。 积分求和在理论和实践过程中起着非常重要的作用。

二、本文的主要工作

第一部分给出积分的一些相关性质， 这些性质将为我们对积分在求和问题中的研究奠定基础。

第二部分利用积分的一般理论来找寻积分在求和应用中的例子。

第三部分利用积分性质， 逐步延深到积分在求和中的应用。

三、预备知识

首先引入了一些性质， 并再借助这些性质简要介绍了本研究领域的发展现状及相关结论。

主要性质

（1）性质，设f是定义在[a,b]上的函数，a＜c＜b， 则f在[a,b]上可积的充分必要条件是f在[a,c]和[c,b]上都可积， 此时

它表示曲线y=f(x)与直线x=a，x=b和y=0围成的图形面积的代数和。

（2）性质设f在[a,b]上连续， 则至少存在一点∈[a,b]， 使得

四、主要结果

本文主要论证的是积分在数列求和中的应用， 下面通过举例阐述应用。

1.积分在数列求和中的应用

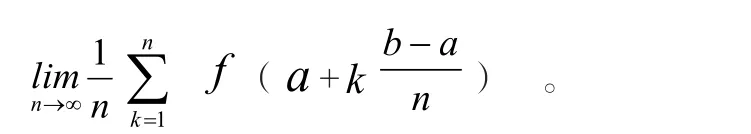
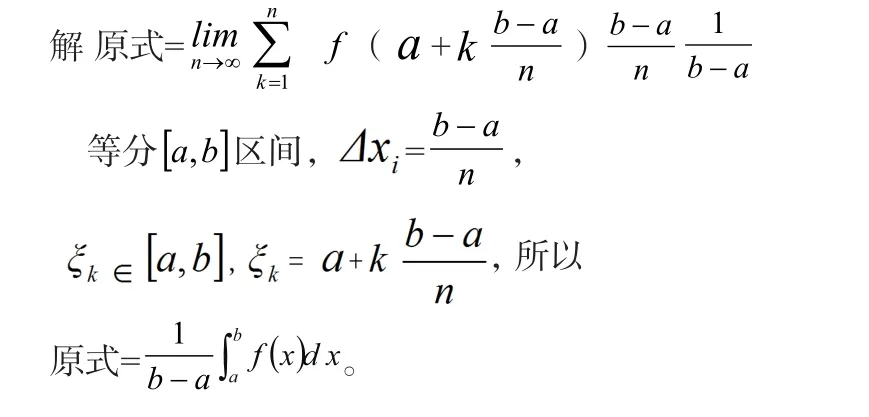
通过上述例子说明， 利用积分直接计算数列的和的问题， 是一种较好的解题方法， 同时， 也使我们认识到初等数学与高等数学之间的内在联系。

2.积分在几何， 经济中的应用

解 利用参数方程

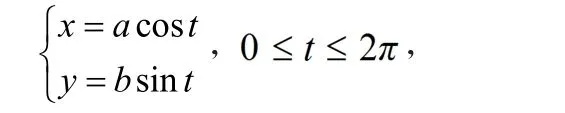
与对称性得

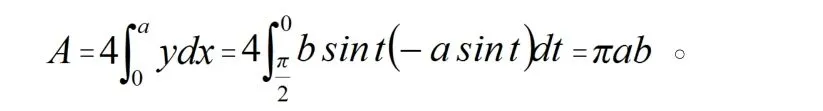
例2 某公司投资2000万元建成一条生产线投产后， 在时刻t的追加成本和追加收益分别为（百万元/年）和=1 7（百万元/年）， 试确定该生产线在何时停产便可获得最大利润？最大利润是多少？

解t时刻的利润

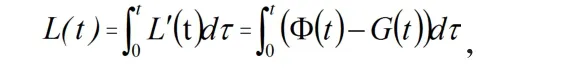
由极值存在的必要条件可知取得最大利润的时刻即最大停产时刻， 应满足L′(t)=0，得，

故生产在投产8年时可获最大利润， 其毛利润为

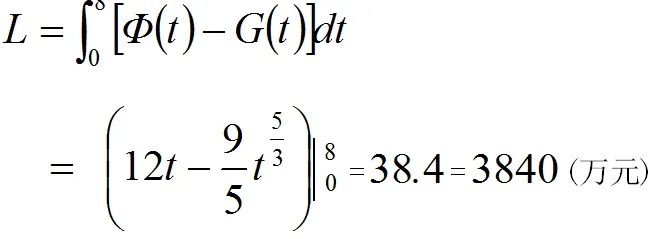
考虑到固定成本是2000万元， 可得最大净利润

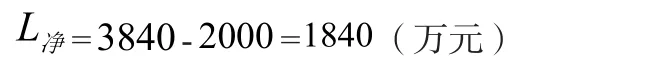
通过上述三例说明， 积分在不同学科内的应用， 是一种较好的解题方法， 同时， 也使我们认识到积分与其他学科之间的内在联系。