找寻“巧合”中的规律——2018年南京市中考第27题感悟

☉江苏省南京市致远初级中学 何君青

☉江苏省南京市致远初级中学 张田田

2018年中考尘埃落定，各地中考试卷相继出炉，南京市中考试卷新颖、独特，历来受到全国各地教育同行的关注.今年南京市中考试卷依然保持一贯的作风，知识覆盖广，区分度适宜.试卷第27题看似简单，却内涵丰富，从求直角三角形的面积入手，继而推广到一般三角形的面积求法，考查可谓独具匠心，看似“巧合”，实则蕴含着规律.笔者对此题进行了深入研究，感悟颇深，故撰文与同行交流.

一、原题呈现

下框中是小颖对一道题目的解答.

题目：如图1，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积.解：设△ABC的内切圆分别与AC、BC相切于点E、F.CE的长为x.根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x.根据勾股定理，得（x＋3）2＋（x＋4）2=（3＋4）2.整理，得x2＋7x=12.所以S△ABC=1 2AC·BC=1 A D 2（x＋3）（x＋4）=1 E O 2（x2＋7x＋12）=1 C F B图1 2 ×（12＋12）=12.

小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积.这仅仅是巧合吗？

请你帮她完成下面的探索.

已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n.

可以一般化吗？

（1）若∠C=90°，求证：△ABC的面积等于mn.

倒过来思考呢？

（2）若AC·BC=2mn，求证∠C=90°.

改变一下条件：

（3）若∠C=60°，用m、n表示△ABC的面积.

分析：本题是三角形、圆的相关知识与思想方法的综合运用，是苏科版教材九年级（上）“切线长定理”的延伸，在教学时，教师会利用此图研究直角三角形的内切圆的相关结论并探索勾股定理.本题有3小问，第（1）问“正着做”，第（2）问“反过来做”，第（3）问“一般化做”，环环相扣，难度逐步上升，题目不仅注重知识之间的连贯性、几何语言的规范性，更注重对学生发散性思维的培养.本题源于教材、高于教材，以文字、表格、图形等方式多样化呈现，有利于学生读懂题、理解题意.从考查内容上看，本题从求直角三角形的面积入手，运用切线长定理、勾股定理解决问题，这些都是中考中的核心考点，注重对基础知识、基本技能的考查，同时注重对基本活动经验、类比思想、逆向思维的考查；从考查方式上看，本题打破以往的考查方式，给予学生适当的解题方法指导，降低了难度，让学生对压轴题的恐惧感大大降低；从考查意义上看，本题的考查注重知识间的连贯性，一正一反地解决问题，让学生对知识的理解更加深刻，也提醒教师在后续授课时需注重知识发生、发展、探究的过程，让学生学到知识，理解知识，会运用知识解决问题.所以，无论从试题基础性、新颖性、公平性、自洽性看，还是从试题的信度、效度、区分度、可推广性看，本题都是一道不可多得的好题.

二、解法剖析

本题的第（1）问和第（2）问做法比较常规，难度不大.第（3）问要求学生要有转化的思想，化斜为直，从而解决问题.第（3）问解法如下.

图2

分析：此法先作出三角形的高，再利用三角函数和勾股定理，求出三角形的面积.从解题教学的角度看，此方法从已知到可知，从要知到需知，拟定可行的步骤成功地解决了问题.此法“源”于学生对方框中方法指导的理解，体现了知识间的连续性.这种解题的步骤源于教师在日常教学中的点滴，要给予学生探索的时间和空间，使学生对数学概念的形成产生痕迹.在上课时，教师需要充分让学生对数学结论发表自己的看法，给予足够的探究时间，学生的数学能力必然会有大幅度的提升.

三、推广研究

为了能将本题研究得更加透彻，从“巧合”中探索出规律，笔者又设计了如下几个问题.

拓展题1：若∠C=45°，用m、n表示△ABC的面积.

解：如图3，过点A作AG⊥BC，垂足为G.

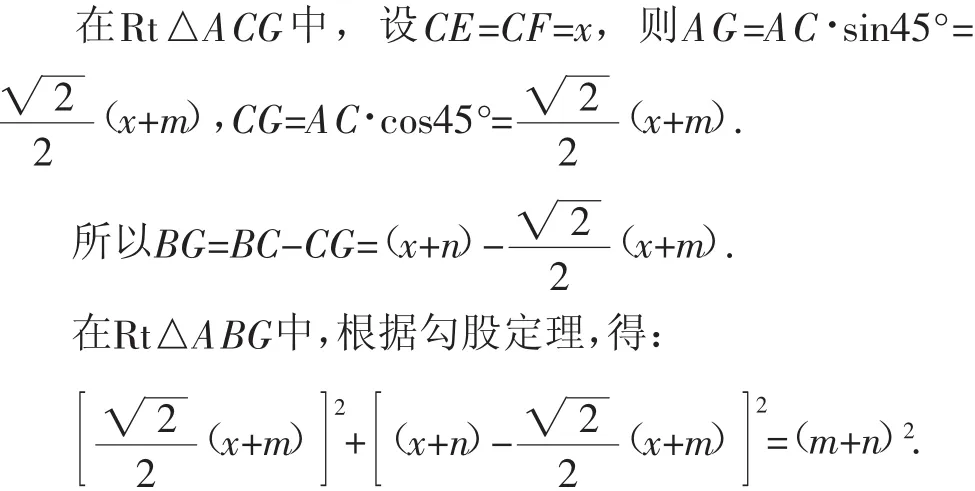
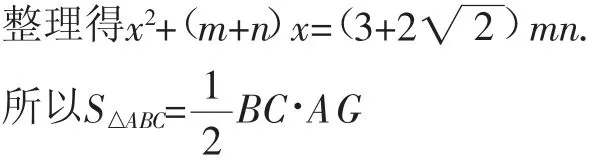
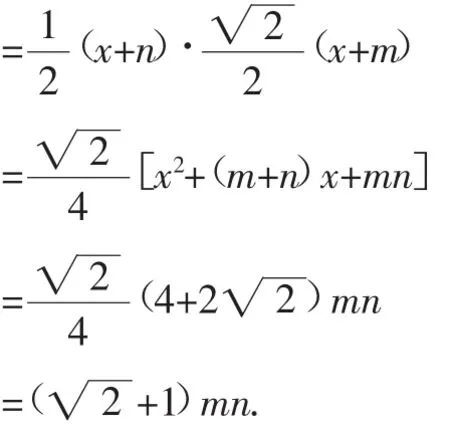
图3

拓展题2：若∠C=α（0°＜α＜90°），用α、m、n表示△ABC的面积.

解：如图4，过点A作AG⊥BC，垂足为G.

在Rt△ACG中，设CE=CF=x，则AG=AC·sinα=（x+m）·sinα，CG=AC·cosα=（x+m）cosα.

所以BG=BC-CG=（x+n）-（x+m）cosα.

在Rt△ABG中，根据勾股定理，得：

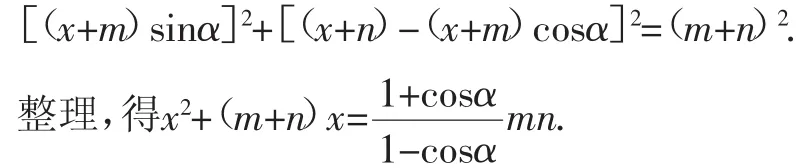
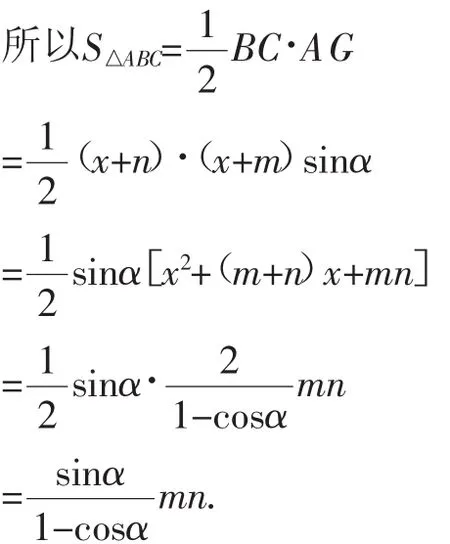
图4

分析：拓展题1将考题中∠C的度数从60°变成45°，方法一致，难度基本相当，区别在于答案中含有根号，计算量比考题有所增加.拓展题2将考题中∠C的度数变得更为一般，用α（0°＜α＜90°）进行了表示，在表达各边时需要用三角函数表达，虽然方法一致，但难度大大增加了.

荷兰数学家弗莱登塔尔提出：学习数学唯一正确的方法是实行“再创造”，也就是由学生本人把要学的东西自己发现或创造出来.故此题在平时教学时需进一步拓展，找寻规律，这样才能让学生真正“会学”，在课堂上实现知识的创新、整合，自主探索、合作交流，根据已有的体验，用自己的思维方式重新创造，得到更多的收获.

四、感悟思考

考试，无论是期中、期末还是中考，都十分注重对基础知识、基本技能、基本思想方法和基本活动经验的考查.对于学习数学，基础是根本的前提，若没有基础，能力的培养和提高则无从谈起.故在教学的过程中，教师不仅要教学手段多样化，更要注重解题方法的多样化，注重通过题组的教学，探寻其中蕴含的数学规律.本题从求三角形面积这一核心考点出发，继而变形、推广，不仅关注数学阅读能力，以及基础知识、基本技能，更让教师在后续的教学中关注学生数学经验的获得，重视基本活动经验的积累，由此可见这道中考题的用心良苦.

1.有利于提高学生的能力

随着学校招生的需要，“功利性”愈演愈烈，应试教育成为很多学校的主要教学方针，凡是中考必考的核心考点就会进行大量的反复训练，中考不考的知识大胆舍弃，不在课堂上提及.这种不良的教学模式对学生能力的培养和后续的发展大有坏处.本题恰好是对这种不良的教学模式的极大冲击，平时的“题海战术”对这类题毫无作用，在题海中“遨游”的学子对于这种题目的解决不占任何优势，反而平时课堂注重知识的形成、发展，喜欢探究的学生占一定的优势，这符合新课标的要求“引发学生的数学思考，鼓励学生的创造性思维的培养”.

在做题时，建议学生多去探索问题中蕴含的数学规律，不要只埋头做题，思考问题时，多经历观察、猜想、分析、综合、归纳和论证等活动，亲身体验知识的发生、形成与发展过程，学会研究的策略和方法，发展探究和归纳的能力，获得终身受益的数学素养.

2.有利于促进教师的发展

中考对后续的教学应起到一定的导向作用，教师在平时教学中应多关注学生能力的培养，致力于教材资源的开发，充分研究命题的规律，注重解题时的一题多解，一题多变.

教师在教学时，要多给学生探索的时间和空间，从题出发，探索题目背后的价值，让一个问题变成一类问题，从而让学生解一题、会一类、通一片.这样的做法也能培养学生主动探究的能力，增强学习数学的兴趣.当学生对数学产生浓厚的学习兴趣时，自然有强烈的求知欲，教学效果更会事半功倍.

一道中考题，看似简单，却又不“简单”，题目看似“巧合”，实则蕴含丰富的规律，让教师明白活用好题、给予学生足够空间和时间的重要性，让学生了解自主探究、领悟数学内涵的学习要义.