“一纸三折”隐玄机 运算推理揭本质——2018年泰州市中考数学第25题命题感悟

☉江苏省泰州市教育局教研室 钱德春

“数学实验”是江苏初中数学教学的特色与亮点，以实验探究驱动数学思维是培养学生数学核心素养的重要途径之一.泰州市2018年数学中考压轴题设置了一道折纸探究问题，试题一面世就在一线数学老师和教学研究人员中引起了强烈的反响.大家见仁见智，一线老师觉得背景新颖，问题出乎预料；专业教学研究人员给予较高评价，福建唐羊老师直言“2018年泰州中考卷出得真不错”，该题特点用一句话概括：“一纸三折”隐玄机，运算推理揭本质.本文结合试题的命制过程、试题特点，谈谈笔者的命题感悟.

一、真题再现

（2018年泰州第25题）对给定的一张矩形纸片ABCD进行如下操作：先沿CE折叠，使点B落在CD边上（如图1-①），再沿CH折叠.这时发现点E恰好与点D重合（如图1-②）.

（2）将该矩形纸片展开.

①如图1-③，折叠该矩形纸片，使点C与点H重合，折痕与AB相交于点P，再将该矩形纸片展开.求证：∠CPH=90°；

②不借助工具，利用图1-④探索一种新的折叠方法，找出与图1-③中位置相同的P点，要求只有一条折痕，且点P在折痕上，请简要说明折叠方法.（不需说明理由）

图1

二、简析简解

试题分为两个大问共三个小问.问题（1）要求根据操作与发现求的比，旨在引导学生初步认识图形，为后续的问题解决积累活动经验.问题（2）①给出折叠方法，要求证明∠CPH=90°.这样设置有两个意图：一是从问题中提取有效信息，根据“折叠”分析线段关系；二是驱动学生思维发展，思考“证明一个角是直角”的常用思路与方法：可由△AED △DHC求得线段长，用勾股定理的逆定理证明，也可以由△AHP △BPC证明，还可以用纯几何方法证明.问题（2）②要求不借助工具探索新的折叠方法，本质上是要求学生在上述活动经验的基础上，对已有方法迁移与创新.这里简要呈现问题（2）①的证明方法.

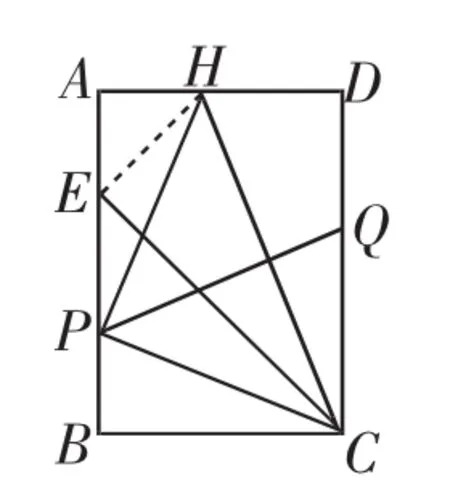
图2

这里AH的长也可由△AED △DHC求得，∠HPC=90°还可用勾股定理的逆定理证明.关键是利用静态图形的特点，设出其中一个量，根据线段关系求出相关的量，再用全等三角形或勾定理的逆定理证明.这种方法没有复杂思维，学生容易入手，是通性、通性，但计算量大，不容易运算到底，对学生的解题心理和运算能力是一种考验.

图3

方法二：几何推理法.如图3，连接ED、HQ.由折叠得：ED⊥CH，PQ⊥CH，易得，所以四边形EDQP为平行四边形，所以DQ=EP.因为QH=QC，所以∠HCQ=故∠QHD=90°-45°=45°，所以 DH=DQ.所以 EP=DH.又因为EB=BC=AD，所以BP=AH.又因为PH=CP，易证△CBP

纯几何推理的方法运用了轴对称、特殊三角形、特殊四边形、全等三角形等基础知识，尽管书写量不算小，但挣脱了烦琐运算的樊篱，思路清晰，线条明快，有畅快淋漓之感.

从试题及分析与解答过程可知，“试题背景”选用学生熟悉的折纸操作；“题干部分”给出操作步骤，“一纸三折”隐含了图形特征、关系等数学信息；“问题部分”设置了从“折叠—运算或演绎—折叠”的设问形式，引导学生探究图形性质，并尝试继续操作；“问题解决”需要对操作后图形的特征、性质认知，通过代数运算与逻辑推理，揭示图形折叠本质；“解答过程”必须先经历基于“折叠”的图形性质探究与证明、再进行以掌握图形性质为前提的新“折叠”；“考查内容”为课程标准所要求的数学基础知识、基本技能、基本思想方法和基本活动经验；“命题意图”旨在体现对“操作—观察—思考—推理—操作”的过程性学习的考查，实现以实验助推思维生长、让理性插上感性翅膀的考查目标.

三、试题前世今生

图4

（1）“一折”.如图4，“先沿CE折叠，使点B落在CD边上”，得到△BCE是等腰直角三角形、四边形BCFE是正方形、CE平分∠BCD，此外，还有一些相等的线段.

（2）“二折”.如图4，“再沿CH折叠.这时发现点E恰好与点D重合”，出现了如下结论：点E与D关于CH轴对称、CE平分∠BCD、CH平

试题命制经历了根据预设找背景、一纸三折隐玄机、选择方向定方案、选择调整再优化和精雕细刻再完善的过程.

1.根据预设找背景

根据预先设定，处于试卷倒数第二题位置第25题，拟从数学实验探究入手，选用江苏省义务教育免费教材《数学实验手册》中的《A4纸中的学问》为背景，从A4纸的特征出发，考查特殊三角形、四边形等有关内容.

2.一纸三折隐玄机

分∠ECD、∠BCP=∠PCE=∠ECH=∠HCD=22.5°，CE=CD，由勾股定理得，△BCP △DCH，进而有

如图5，如果将△ABE剪下拼到△CDF位置，可得四边形BEFC是菱形，由此又能衍生出新的结论.

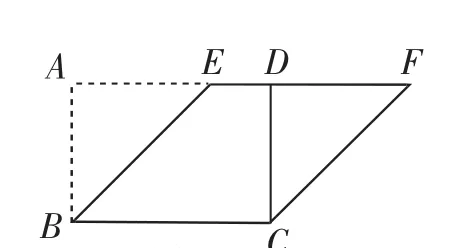
图5

（3）“三折”.如图6，“折叠使点C与点H重合，折痕交AB于点P”，连接EH、QH、ED可得：△AEH、△QDH是等腰直角三角形，CH垂直平分DE、四边形EPQD为平行四边形，△APH △BCP，点P为以CH为直径的圆与AB的一个交点 ，BP=AE，PC 平 分 ∠BCE，PQ=PC=PH、点H、E、P、C在同一圆上、点T是△HPC的内心……

由此可见，此折纸问题隐含的图形性质、结论较多，隐藏了玄机.根据这些特点，问题可以向不同方向发展.

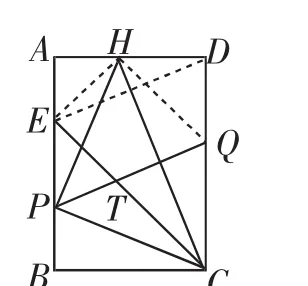
图6

3.选择方向定方案

方向一：如图5，将图中的△ABE沿折痕剪下，拼到△DCF的位置.

（1）证明四边形BEFC是菱形；

（2）如图7，设P、Q分别是BC、CF上两点，且∠PEQ=67.5°，探索BP、PQ、QF三条线段之间的数量关系，并说明理由；

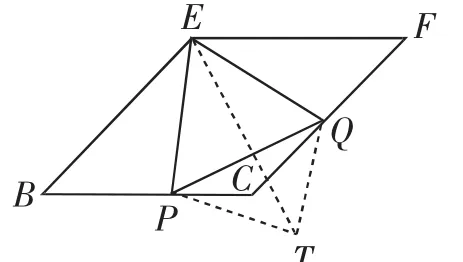
图7

（3）在（2）中，设AB=a，（BP+2a）（QF+2a）的值是否变化？并说明理由.

线段BP、PQ、QF之间的数量关系为BP2+FQ2=PQ2，图形是典型的“半角模型”，坊间流传甚广，其证明方法主要是“翻折”或“旋转”，有基本的“套路”可循.另外，“（BP+2a）（QF+2a）等于定值”问题是“变中不变”的问题，具有较浓厚的数学味儿，美中不足的是：结论系上一结论经过计算而得，知识单一、思路狭窄，难以承载作为中考压轴题应有的份量.

方向二：从“重心”角度考虑.

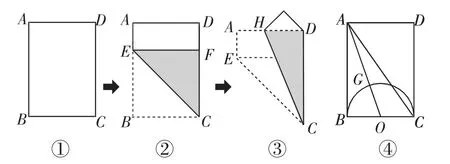
图8

方案一：将一种型号的长方形纸片ABCD（如图8-①）按如下步骤操作：

第一步：如图8-②，沿CE折叠，使点B落在CD上的F点.

第二步：如图8-③，沿CH折叠，点E恰好落在点D处.

（1）求证：四边形BCFE是正方形.

（2）若AD=1，求CD的长及tan∠DCH的值.

（3）我们知道，三角形两条中线的交点就是三角形的重心.如图8-④，以BC为直径在长方形纸片ABCD内作半圆O，与AO相交于点G，求证：点G为△ABC的重心.

第（1）问是一道基本的几何证明题；第（2）问根据给定一条边长进行计算，学生容易上手得分，也为第（3）问的解决作有效铺垫；而第（3）问先交代“重心”定义，旨在引导学生用定义证明“重心”.图8-④中AO已知是BC边上的中线，只要再证明G在另一边的中线上即可.学生可能有两种选择，一种选择是连接并延长CG交AB于点M，证明M为AB边上的中点，通过代数运算或几何推理解决；另一种选择是连接并延长BG交AC于点N，同样可证明点N为AC的中点.但若连接BD交AC于点N，由“矩形对线互相平分”知N为AC的中点，则要证明DB经过点G，对初中学生而言就勉为其难了，故再作调整.

方案二：（2）（条件与方案一中的问题（1）与上述问题相同）在图8-③中，若AD=a，求的值，并用含a的代数式表示△CDH的面积.

（3）我们知道，三角形两条中线的交点就是三角形的重心.如图9，以C为圆心、BC长为半径画弧交BD于点G.求证：点G为△ACD的重心.

图9

这种调整虽然解决了上述困惑，但再三推敲后发现：“重心”内容在课程标准中属于“了解”层次，尽管题干特地说明了“重心”的概念，并且试题主要是用重心定义证明，而不是考查重心性质的应用，然而，由于中考试题是教学的风向标，作为压轴位置的试题，将“重心”这样的非核心知识作为考点，会对教学产生误导，因此最终还是忍痛割爱了.

方向三：从图形面积上思考.

如图10，以C为圆心、BC长为半径画弧交BD于点G，求△ABG的面积.

问题很快被破解：作CM⊥BD于点M，通过计算易得BM=MG=GD，从而有△ABG的面积等于△ABD的面积的，至此问题被“秒杀”，显然没有达到压轴题应有的区分度要求.

图10

方向四：操作→推理或运算→操作.

试题是以“折叠”为背景的，前面的问题由“折叠”产生，为了保证问题形式的一致性，接下来的问题还回到“折叠”上来.

（3）（条件与方案一相同）图1-④中的CE、CH为上述操作的折痕，利用图1-④的纸片再折叠一次得到点P（点E除外），使△PCH是以CH为斜边的直角三角形.请在图上画出折痕，简要说明折叠方法，并说明理由.

问题中的点P的位置如何找？可以有两种探究方法.

一是以CH为直径作⊙O与AB相交于两点（如图11），其中一点为E，另一点为S，∠CSH也为90°.进而可联想到：作OM⊥AB于M，则EM=SM，由梯形中位线定理得AM=BM（要证明），则有AE=BS，即只要在AB上取一点S，使BS=AE，这个点S即为所求的P点.

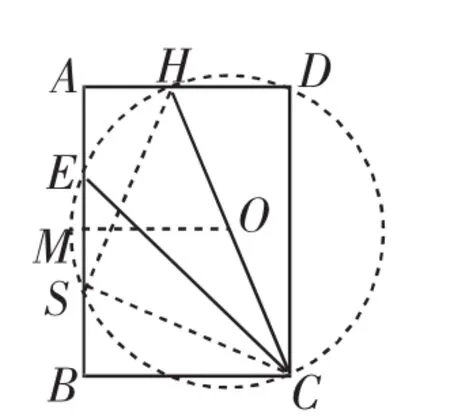
图11

二是通过三角形相似找点P.假设点P就是所求的点，则有△BCP △APH（如图12），于是有：设BC=a，计算得CD=设BP=x，所以有解得1）a或a.满足x=a时的点即为E点，故点P为使PB=1）a的点.

图12

以上是通过计算或推理得到点P的位置，如何回归到“折叠”的方法上来？有如下方法：

方法一：如图13-①，折叠使AD边落在CD边上，折痕交AB于点P；

方法二：如图13-②，折叠使AD边落在AB边上，点D的对应点即为点P；

方法三：如图13-③，将矩形ABCD对折，使AD与BC重合，点E在AB上的落点即为点P；

方法四：如图13-④，折叠使BC边落在CE上，折痕交AB于点P；

方法五：如图13-⑤，折叠使点C与点H重合，折痕交AB于点P.

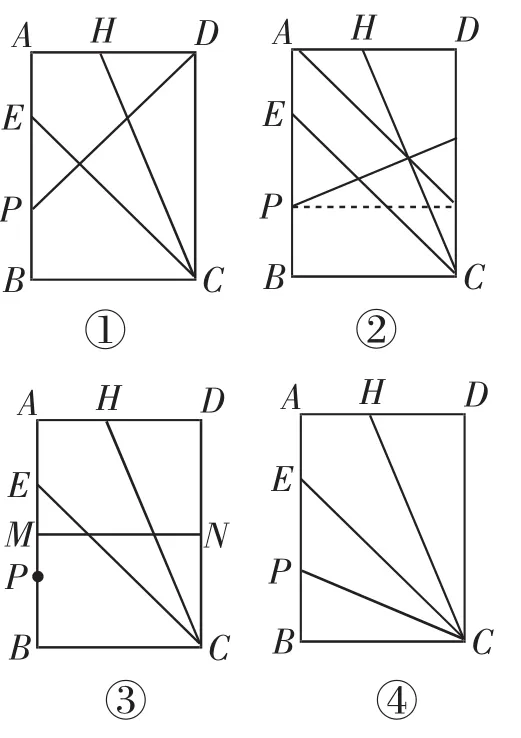
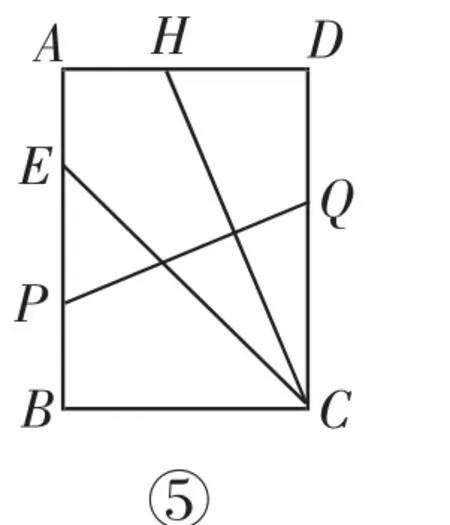
图13

……

此外，问题还可以通过多次折叠来解决.那么“折叠”的理由何在？与运算和推理等探究的方法、结论有何关联？换言之，如何将运算与推理的结论与图形折叠“无缝对接”？

显然，由“点P为以CH为直径的圆与AB的另一个交点、BP=AE”得到“AP=BE=AD”，由此可以得到“方法一”“方法二”“方法三”；由“∠BCP=∠PCE=22.5°、”联想到△PCH为等腰直角三角形，进而得到“方法四”“方法五”.事实上，所谓的“折叠”，其思路还是来源于对图形性质特征的认识和探究活动经验.

但是，试题的命制与解题教学有本质的区别，前者侧重结果，后者侧重过程.命题者既要考虑试题探究的过程性、思路的开放性和方法的多样性，更要考虑阅卷的可操作性与评价的标准性，因此必须适度开放与适当减少答案的多种可能性相结合.因此问题增加了两个限制：一是只进行一次“折叠”，二是强调一定要是“折痕与AB的交点为P（点E除外）”.如此，符合要求的“折叠”只有“方法一”“方法四”“方法五”这3种方法.

4.选择调整再优化

纵观试题的3个问题：发现整个试题是从操作到操作，缺少逻辑推理要求，这样的几何试题显得不够完美.遂将原问题（2）改成关于“折叠”操作结论的证明题，即“（2）①如图1-③，折叠该矩形纸片，使点C与点H重合，折痕与AB相交于点P，再将该矩形纸片展开.求证：∠CPH=90°”，并追加“问题（2）②”，通过新的“折叠”方法继续操作，找出相同的点P，这样就适当控制了方法的多样性，问题形式也在“折叠”上一脉相承、一以贯之.

5.精雕细刻再完善

大的方向与问题形式确定后，接下来就是问题细节的处理，如呈现方式、文字表述等问题的推敲、雕琢，以尽可能达到准确、完善.

（1）试题背景如何呈现？

尽管学生几乎每天都有可能接触A4纸，但是，如果不细心留意，学生不会对这样的背景有“感觉”，这样的背景就不太公平.故试题干脆不提及“A4纸”的名称，而是通过折叠操作，用“发现”的结论求该纸片两邻边的比，为后续问题解决奠定基础.这样，试题背景经历了“A4纸”→“给你一张矩形纸片”→“对于给定的矩形纸片”的调整过程.这里的“给定”意在说明“纸片”是命题者设定好的特定矩形纸片，而不是“任意”纸片.

（2）操作方式如何描述？

原来题干的“操作”过程这样描述的：“第一步：沿CE折叠，使点B落在CD边上；第二步：沿CH折叠，点E恰好与点D重合.”事实上，“点E恰好与点D重合”不是“折叠”出来的，也不是任意型号的纸片都具有的特征，而是“对于给定的特定的纸片（A4纸）”才有的.因此，将题干改为操作后“发现点E恰好与点D重合”.

（3）是否将“折叠”后纸片的重叠部分画上阴影？

根据学生《数学实验手册》上的图形，对折叠后的重叠部分加了阴影（如图8-②和8-③），但图上的阴影会对学生利用图形探究造成干扰，在最终呈现的试题中去掉了阴影.

（4）为什么要将“折叠”后的纸片展开？

最初试题提供了“折叠”后的图形，如果这样，解题者难以在该图上发现和证明结论，故加上“将该矩形纸片展开”的操作，在“展开”的纸片上保留“折叠”的痕迹，既合情合理又便于学生探究.

（5）问题（2）①如何设问？

原来问题（2）①是要求“判断折叠后的△PCH的形状，并说明理由”.事实上，△PCH是一个等腰直角三角形，如果学生回答“直角三角形”，算正确吗？这就会引起理解歧义，给评分带来麻烦，本着“存疑即否”的命题原则，将“判断△PCH的形状“改为“求证∠CPH=90°”这样的设问方法指向更具体.

（6）问题（2）②的再操作问题如何叙述？

该题本意是以“再折叠“形式考查学生对图形性质与特征的再探究、再认识.但具体命题中需要考虑：一是如何折叠？折叠几次？从前面分析来看，仅“一次折叠”就有五种方法，如果允许多次折叠则方法更多，这就有一个多种可能性如何控制的问题；二是如何将折叠过程在图形上体现出来？要不要画图？图如何画？如果画图，是否允许使用工具？如果使用工具，如何用？理论上需要尺规作图，这与命题本意相悖；三是如果不使用工具画图，那又会出现什么问题？显然图形的随意性使问题失去了数学的严谨性；四是如何制定评分细则？这些问题都需要认真对待.经思考最终敲定：“不借助工具，利用图1-④探索一种新的折叠方法，找出与图1-③中位置相同的P点，要求只有一条折痕，且点P在折痕上.请简要说明折叠方法（不需说明理由）”，这样就重点考查数学思维，画与不画不影响得分.

四、命题感悟与反思

应该说，数学实验试题的命制是一次初步尝试，通过实践，笔者体会到：数学实验是数学思维的催化剂，实验操作有时是基于学生已有的认识与经验，操作问题要体现“三个能级”要求，回归数学本真，准确把握实验真实与数学简约之间的关系，顺应解题心理，设置合理的上行阶梯.

1.数学实验是数学思维发展的催化剂

本题从形式上看是一个几何操作探究问题，试题背景取自于初中数学实验手册，试题沿着“操作探究—运算与推理—操作探究”的轨迹发展，整个问题体现了“做数学”的理念，通过数学实验引导数学思维.因此试题也可以看作数学实验问题.数学实验问题有两种类型，一类是通过实验来探究结论并用数学知识验证结论，另一类是用实验的方法直观地验证逻辑推理得到的数学结论.本题两种类型兼而有之.第（1）问根据“折叠”操作的图形求线段的比，第（2）①问判断和证明“折叠”操作后图形的形状，这属于操作探究型实验，第（2）②问则是基于对图形认识的新的操作，实际上是对已有数学认知的实验验证，属于直观验证型.由此发现，无论何种类型，数学实验的根本目的是助推数学思维的生长.因此，试题要把握好数学实验与数学思维之间的关系，不能为实验而实验，而要通过数学实验促进学生思维能力发展.

2.图形操作基于已有认知与活动经验

试题看似折纸实验，实质上问题的解决必须依赖于对折纸中所隐藏的图形位置与数量关系的认识与理解.如图形折叠后，有些结论，如等腰直角三角形、正方形、22.5°等可以通过实验现象直观发现，而更多的问题或结论则需要通过深刻分析，经由数学计算或推理才能获得.

3.操作探究体现知识“三个能级”要求

喻平教授把数学知识分为三个能级，即知识理解、知识迁移和知识创新.本试题第（2）①的证明方法多样，思维入口宽，不同思维层次的学生可以有不同的解法.如第（2）①问既可以用代数方法运算推理，也可以用纯几何方法演绎推理；第（2）②问要求继续“折叠”，实际上是要求对前面的操作经验与方法进行新的迁移，体现出对数学知识的理解、迁移与创新的能力要求.这应该成为今后命题的方向和要求.

4.数学实验试题命制要回归数学本真

试题命制最初出现了“重心”的问题，这不是初中数学的核心内容，容易产生不良价值导向，于是命题组及时调整.经历这个过程，笔者体会到：无论试题形式如何、难度怎样，命题一定要依标据本，基于初中数学课程标准和教材，基于学生的认知基础，问题的解决方法要回归到初中数学的基础知识、基本方法，不能突破“天花板”.

5.力求兼顾实验的真实与数学的简约

既然是数学实验，就应该设置真实的实验背景、体现真实的操作过程，这就带来问题的多变性与复杂性.而数学的特征之一就是简约.因此，如何兼顾数学实验的真实性与数学问题的简约性是数学实验类试题命制的难点.

比如，本题图形“折叠”后的多线条对学生解题就是一把双刃剑.一方面这些线条为问题解决提供了思路.可以设想：如果将图中的CE删去，就相当于抽掉了登高的木梯；另一方面线条多又对问题解决造成了一定的干扰.因此，从命题角度看，试题要尽可能体现对学生的人文关怀，减少对学生的思维干扰；从教学角度看，需要增强学生抗干扰的能力，培养学生提取有效信息的能力和“数学模型”意识，问题（2）①的图形就可以分解为多种基本图形.

又如，本题的操作限定在长与宽之比确定的矩形中，所以操作后所有图形的形状、位置与数量关系都是确定的，所有的线段长度、角的度数、封闭图形的面积等都可以通过计算获得，因而学生想到用代数运算方法解题应该是一种自然选择.但这样又出现思路单一、过程繁杂的现象，在一定程度上影响学生的解题信心.因此，从命题角度看，试题可以设计成代数方法、几何方法都容易入手的形式；从教学的角度看，要注意渗透数形结合思想，形的问题尝试用数的方法解决，数的问题尝试从形的角度思考，还要引导学生交叉进行，以达到融会贯通的效果.

6.试题命制必须设置合理的上行阶梯

从实测数据看，该题均分3.9，难度系数为0.325，0分的占31.1%，满分的只占0.4%，出乎命题者的预料.从思维难度上说，如果第（1）问设置长度、面积或三角函数值计算问题，可为后面问题探究做铺垫，减缓试题的坡度，但这又会将学生引入到代数运算的“独木桥”上来；如果不设置“计算”台阶，学生的思路可更开放、多样，结果又导致部分学生“跳一跳够不到”，这两个问题让命题者处于两难的境地.命题既要考虑考查目标、区分度和试卷构成，也要了解、把握学生的认知基础和能力，在学生最近发展区内命题，设计合理的梯度和难度，让学生有上行的台阶.这些都需要命题者更多的思考与实践.