结论与过程 相辅又相成

安徽省萧县中学 (235200)

郝文华

“以生为本”是新课程的一个重要理念，学生的数学学习活动，不应只局限于简单的接受、记忆和模仿训练，而应倡导自主探索、动手实践、合作交流的学习方式，让学生在探索中体验数学知识发现和创造的历程，这也是培育数学核心素养的重要渠道.在教学中，教师如果一味地包办代替，只注重结论的呈现，而不重视知识的来龙去脉，将不会达到理想的教学效果.事实上，结论与过程应该是一个相辅相成的关系，下面就此问题，结合笔者多年的教学实践，谈几点看法.

一、知识的推导过程宜严密细致，不应简而概之

俗话说，细节决定成败.对于一些知识的产生、发展与证明都要有严密的逻辑过程，而不应纯粹为了获取一个结论而直奔主题.事实上，这种推理过程，本身就具有极高的体验价值，其蕴含的思想方法及处理问题的策略，均是值得学习与借鉴的.例如，在推导等差、等比数列的求和公式时，教材中利用了倒序相加和错位相减的处理策略，这些方法不是纯粹为了推导求和公式而设定的，它本身就是一种求和策略，而这种策略对于解决一些其他数列求和问题具有极高的应用价值.再如，在圆锥曲线的学习中，对椭圆、双曲线和抛物线方程的推导过程，本身就是求曲线轨迹的一种方法.可以说，只有明白了知识产生发展的起因与过程，才能突显数学教学的本质.

又如，在三角函数的教学中，辅助角公式是一个非常重要的知识点，但在实际教学中首先要明确的一个问题就是为什么要学习辅助角公式，也就是说，辅助角公式产生的背景是什么？明白了这一点，学生在做题时才能想到去利用这个公式.否则，即使学生知道有这个公式的存在，也未必能想到去应用.这就需要教师在实际教学中，要注意引导学生去寻求这个辅助角公式的产生背景.那就是，形如f(x)=asinx+bcosx的函数，其结构上是关于正余弦的线性组合，为了研究其各种性质，就需要将其转化为类似于函数f(x)=Asin(ωx+φ)的结构形式，这就需要利用辅助角公式来进行转化，其过程如下：

f(x)=asinx+bcosx=

例1 (2013年全国Ⅰ卷)设当x=θ时，函数f(x)=sinx-2cosx取得最大值，则cosθ= .

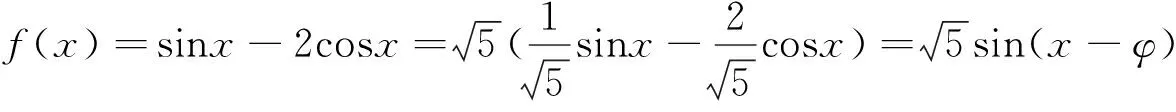
由此可见，单纯的记忆辅助角公式，只能解决形如函数f(x)=asinx+bcosx的一些简单的性质问题.对于一些复杂的问题，还需对辅助角公式的内涵有所了解.

二、结论的直接呈现与记忆，无法让学生真正掌握知识

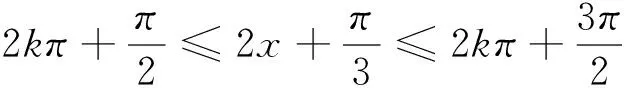
由此可见，只有深度了解知识的来龙去脉，才能以不变应万变，才能避免出现重形式而不重实质的“假理解”现象.

三、教学中要多角度、多渠道地展现过程性教学

为了更好地体现过程性教学，教师课前就要充分预设，精心准备.授课中要尽可能地让学生主动观察、分析、猜想、归纳、概括等发现和探索过程，鼓励学生探讨其他可能的解答思路.引导学生课前预习教材，教材是学生获得知识的重要途径，也是教师授课的“根本”.通过阅读教材，可以看出哪些知识需要讲解过程，哪些知识需要一带而过，教师要做到心中有数，详略得当.例如，在二项式定理的讲授中，定理的引出是以多项式相乘展开的，首先提出问题：计算乘积(a1+b1)(a2+b2)(a3+b3)，并思考乘积中的每一项是怎样得到的.

不难得到(a1+b1)(a2+b2)(a3+b3)=a1a2a3+a1a2b3+a1b2a3+a1b2b3+b1a2a3+b1a2b3+b1b2a3+b1b2b3.

引导学生观察：所得的八项有一个共同特征，那

授课中，如果老师不讲或淡化上述引入过程，而直接给出二项式定理，然后让学生去记忆式子的结构和相关性质，就无法真正的掌握二项式定理的内涵.事实上，这个引入是二项式定理产生过程的主要体现，只有充分理解了多项式相乘的规律，才能从实质上把握二项式定理的结构.

(A)15 (B)20 (C)30 (D)35

由以上可以看出，过程性教学无论是在概念的理解上还是在解题上都是至关重要的一个环节，也是培养学生思维能力的主要渠道，更是培育数学核心素养的动态过程，在实际教学中，不可轻视.