采用电抗子模块分段投切的模块化多电平换流器降电容方法

李 钰, 李 帅, 赵成勇, 许建中, 曹均正

(1. 新能源电力系统国家重点实验室(华北电力大学), 北京市 102206; 2. 中电普瑞电力工程有限公司, 北京市 102200)

0 引言

模块化多电平换流器(modular multilevel converter,MMC)拥有模块化、可靠性高、开关频率低、波形质量高、制造难度低等优势[1-4],为柔性直流输电技术提供了更广阔的应用空间。

作为传统柔性直流输电中采用的集中大电容的替代,MMC用分布于各个子模块的小电容来支撑直流电压,更易于制造。但在实际应用中也产生了一系列问题：由于分布电容之间的能量不均,进而引发上下桥臂能量不均衡分布,使子模块电容电压波动难以抑制,增加了换流器损耗,使交流侧输出电压出现偏差,影响波形质量。

电容器在整个换流站的占地面积和建造成本中占比很大。如果仅依靠提高电容器容值来降低电压波动,会使其体积和成本大大增加,经济性较差。因此针对MMC探索新的方法来降低子模块电容波动,对减小换流器占地面积和建设成本具有重要的现实意义。

对于MMC电容电压波动的抑制方法,国内外学者提出了许多有效的解决方案,目前主要分为控制方案和拓扑方案两种。

从附加降容控制角度：文献针对桥臂上存在的二倍频环流分量,设计了环流抑制控制器,经过二倍频负序的旋转坐标变换的比例—积分(PI)控制器,有效地抑制了二倍频环流,但没有抑制其他次数环流产生的电压波动;文献采用2次环流注入方法,通过离线最优化计算得出电压波动最小时对应的环流参考值幅值和相位;文献在文献基础上,同时注入2次和4次环流分量,通过遍历的方法计算了各分量的最优参考值,效果更好。但文献[6-7]的最优化计算均属离线计算,实际应用时存在困难;文献从能量角度出发,设计了dq解耦双环控制器,在线控制使桥臂能量波动最小来降低电压波动,实质也是注入负序二倍频环流,但控制器较为复杂;文献提出两种根据MMC的输出电压指令值和输出电流瞬时信息在线计算2次环流参考值的方法,但是对注入环流降低电容电压波动的机理并未做深入分析。文献[10]提出一种直接控制环流来抑制电压波动的方法,根据相电流的瞬时值与相电压调制值得到环流2次分量的参考值,并使用陷波器得到两倍频分量,引入准比例—谐振(PR)控制器进行环流闭环控制,控制器较复杂。以上控制方法主要依赖于对2次环流的控制。文献[11提出调制波注入3次谐波的方法,可进一步降低换流器损耗以及子模块电容电压波动。从降容拓扑角度：文献[12]提出通过采用半桥加全桥混合子模块及相应均压策略,可使换流器电压调制比升高,实现子模块电容电压波动幅值的降低。文献[13]分析了半全混合MMC拓扑下的子模块电压波动,并推导出波动最小的工作点,且针对无功功率增加引起的电压波动提出了抑制策略。文献[14]提出了一种含中间子模块的MMC改进拓扑,其中间子模块不含基频电压波动,顶部子模块和底部子模块不含基频与二倍频电容电压波动,但该方案需要对MMC子模块重新改造。文献[15]将控制方案与拓扑方案相结合,提出利用环流注入方法及混合MMC拓扑特有的提高交流电压的方式,可以有效地降低对直流电容值的要求。

本文首先分析了考虑2次和4次环流分量的MMC子模块电压波动产生机理;从拓扑角度提出了以子模块形式分段投切桥臂电抗器的降容方案,分析了方案的原理;设计了相应的控制策略;在PSCAD/EMTDC平台下进行仿真实验,验证了方案的有效性,并将其与环流抑制控制方案的作用效果进行了对比。

1 MMC子模块电容电压波动分析

文献[16]中对子模块电容电压波动的产生机理进行了数学分析,但没有推导二次环流及更高次分量对子模块电压波动的影响。在半桥MMC拓扑中,假定MMC的3个相单元的参数完全相同,每相上、下桥臂参数对称,则可以认为直流电流在3个相单元中平分,交流电流在上、下桥臂平分[17]。忽略内部环流,上下桥臂电流可以表示为：

(1)

(2)

式中：Idc为直流母线电流;iuj和idj分别为上、下桥臂电流;Ivj为交流侧电流幅值,其中j=a,b,c;ω为基波角频率;φ为初相角。

但实际上,桥臂电流中除了直流分量和基频交流分量,还含有偶数次谐波分量形式的内部环流[18],其中2次环流幅值占比最大。由于其他次数环流对子模块电压波动的影响较小且可类推,本文只计及2次环流和4次环流,以a相为例,此时上下桥臂的电流可以表示为：

I4fcos(4ωt+φ4f)

(3)

I4fcos(4ωt+φ4f)

(4)

式中：I2f,I4f和φ2f,φ4f分别为2次环流、4次环流的幅值和相角。

上、下桥臂的开关函数可分别表示为[16]：

(5)

(6)

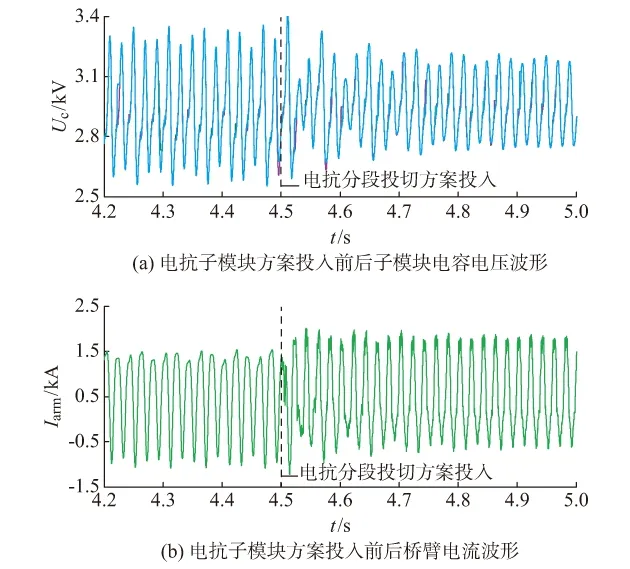
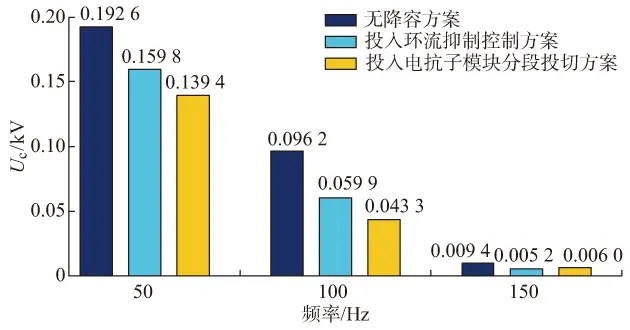
式中：m为调制比,定义为m=2U/Udc,通常情况下有0

假设排序频率无限大,则各子模块电容电压保持一致,任意时刻通过上下桥臂任意子模块电容的电流值为：

(7)

(8)

式中：C为子模块电容的容值;ucua和ucda分别为上、下桥臂任意子模块的电容电压。

考虑到子模块能量不能无限积聚,即式(7)和式(8)中的直流项应为零[10],则有

(9)

由式(7)和式(8)可以看出,考虑到2次、4次环流时,子模块电压应含有从基频到五倍频的波动项,且上下桥臂的2次、4次分量相位相同,1次、3次、5次分量相位相反。上下桥臂任意子模块的电压可分别表示为：

ucua=Ucref+UcrefΔU1sin(ωt+φ1)+

UcrefΔU2sin(2ωt+φ2)+UcrefΔU3sin(3ωt+φ3)+

UcrefΔU4sin(4ωt+φ4)+UcrefΔU5sin(5ωt+φ5)

(10)

ucda=Ucref-UcrefΔU1sin(ωt+φ1)+

UcrefΔU2sin(2ωt+φ2)-UcrefΔU3sin(3ωt+φ3)+

UcrefΔU4sin(4ωt+φ4)-UcrefΔU5sin(5ωt+φ5)

(11)

式中：Ucref为子模块电容电压的额定值,Ucref=Udc/N，其中N为上下桥臂子模块总数;ΔUi(i=1,2,3,4,5)表征了各次分量的波动幅度;φi为各次分量相角。

则对式(7)和式(8)求积分,可得ΔUi为：

(12)

(13)

(14)

(15)

(16)

式中：x0至x3变量展开式如附录A式(A1)至式(A4)所示。

上下桥臂电压可分别表示为：

uua=NucuaFmua=Uuadc+Uua1cos(ωt+φ1′)+

Uua2cos(2ωt+φ2′)+Uua3cos(3ωt+φ3′)+

Uua4cos(4ωt+φ4′)+Uua5cos(5ωt+φ5′)+

Uua6cos(6ωt+φ6′)

(17)

uda=NucdaFmda=Uuadc-Uua1cos(ωt+φ1′)+

Uua2cos(2ωt+φ2′)-Uua3cos(3ωt+φ3′)+

Uua4cos(4ωt+φ4′)-Uua5cos(5ωt+φ5′)+

Uua6cos(6ωt+φ6′)

(18)

式中：Uuai为桥臂电压各次分量幅值(i=1,2,3,4,5,6);φi′为各次分量相角。

由式(10)和式(11)的推导过程可以看出,即使假设桥臂电流中不含环流分量,直流电流和基频电流也会因为全控器件的开断而产生基频和二倍频的电容电压波动分量。上下桥臂电压之和即为相单元总电压。由于各相单元上的二倍频电压波动不等,电压差将作为电源产生二倍频的环流分量。该环流将产生更高次数的电压波动分量,新产生的电压波动又作为电源产生相应次数的环流分量。

由式(12)至式(16)可以看出,子模块电容电压的基频波动幅度与基频电流幅值和2次环流幅值有关;2次分量波动幅度与基频电流幅值、2次环流幅值有关;3次分量与2次环流幅值、4次环流幅值有关;4次、5次分量均与4次环流幅值有关。因此,单纯将内部某次环流抑制为零,无法消除其余频次电流对电压波动的影响,不是电容电压波动抑制的最优解[19]。且因为大部分谐波分量幅值均与基频电流值有关,进而与传输功率有关。当子模块电容值有限而传输功率增大时,电容电压波动会随之增大。

2 电抗子模块分段投切控制方案

由上文可知,子模块电容的电压波动实际是由桥臂电流引起的,若要让电流流过电容,必然存在电压波动。由各相单元之间存在电压差,即上下桥臂电压之和并不完全与直流电压Udc相等而产生的环流进一步增大了电压波动。通过对桥臂电抗器进行投切控制,可以改变桥臂中的能量分配,进而改变桥臂各次电流值,抑制子模块的电容电压波动。

2.1 电抗分段投切方案拓扑结构及运行方式

针对桥臂电抗器元件,提出一种在上下桥臂控制投入不同数目的电抗器,改变环流在上下桥臂之间的分配,从而抑制子模块电容电压波动的方案。方案采用的MMC拓扑如图1所示。

图1 含电抗子模块的MMC拓扑Fig.1 Topology of MMC with reactance submodules

在MMC半桥换流器基础上,方案将原本的桥臂电抗的整段固定接入改为分多段灵活投入,即把每个桥臂上的桥臂电感分为固定投入部分L1和多个可控投切的电感Li(i=2,3,…,n)。其中每段灵活可控的电感L0构成一个电抗子模块(LSM),以提高可靠性。各段桥臂电抗器串联构成该桥臂上的总电抗。电抗子模块内部结构如图1所示,通过对其内部的开关器件的控制,可以使电抗子模块内的电感投入或切除,从而改变上下桥臂分别串联的电抗值。

2.2 电抗器分段投切方案原理

桥臂电抗对桥臂电流有较大影响[17],当上下桥臂电抗值不同时,可以较大程度上影响上下桥臂的电流分布。以a相为例,假设通过桥抗投切控制,上桥臂投入naup个电抗子模块,其上桥臂电抗值比下桥臂投入的电抗值小。设两桥臂投入电抗值之差为ΔL,则有

Laup=naupLi+L1

(19)

Ladown=Laup+ΔL

(20)

式中：Laup和Ladown分别为上、下桥臂电抗值。

如附录A图A1所示,上下桥臂分别有

(21)

(22)

式中：uka为交流电网侧电压,有uka=Ukcos(ωt+θ);uua和uda分别为上、下桥臂的桥臂电压；LT为变压器漏电感。

可求得上、下桥臂电流分别为如附录A式(A5)和式(A6)所示,容易得出随着上桥臂电抗值的减小,桥臂电流的有效值将随之增大,并大于下桥臂的输出电流。

MMC上同一时刻上下桥臂投入的MMC子模块总和始终为N,各子模块相互串联,因此任一时刻接入的子模块的充放电速率相等,而只有接入的子模块电容才会产生电压波动。假设排序频率足够高,各子模块的电容值相同,则同一时刻桥臂等效电容值与投入的子模块个数之间的关系可以表示为：

(23)

式中：Ceq为该桥臂对外等效电容;n为处于投入状态的子模块数量;C0为子模块的电容值。

可以看出,投入的子模块数量越少,桥臂等效的电容值越大,因此其子模块电容电压波动幅度也小于子模块数量较多的桥臂。因此可通过增加投入数较少的桥臂的分流,抑制另一桥臂电流的方式降低整体电容电压波动幅值。

同时,为避免由于各相单元的总电抗值不同而引起更多的环流,在控制投切时要保证上下桥臂投入的电抗之和保持恒定值。

将式(A5)和式(A6)改写成包含偶次环流分量的形式,则a相上下桥臂电流可以表示为：

cos(2ωt+φ2f)+(I4f+ΔI4)cos(4ωt+φ4f)

(24)

cos(2ωt+φ2f)+(I4f-ΔI4)cos(4ωt+φ4f)

(25)

式中：ΔIi为各次分量幅值的变化量。

结合式(12)至式(16)可以看出,电抗子模块分段投切方案可以对子模块电容电压各次分量起到抑制作用。

2.3 电抗器分段投切方案控制策略

由于绝缘栅双极型晶体管(IGBT)和二极管通流能力的限制,为了保证器件的安全裕度,应确保桥臂投入电抗个数较少的半个工频周期的桥臂电流不超过器件额定值,因此可通过所采用IGBT的参数来作为上下桥臂投入电抗数差值的选取约束之一。同时,由于不同传输功率下桥臂电流值不同,相应的约束条件也不同,因此有必要使投入电抗差值可以根据需要改变,从而使任何工况下都能在达到最优降容效果的同时满足可靠性的要求。考虑到桥臂电抗及抑制故障下的桥臂电流上升率的作用,为保证采用本方案不会影响抑制效果,应该将上升率约束作为此时相总电抗值(L1+2L2)的选取依据。

因此,控制策略应能实现以下两种功能：①为避免各相单元总电抗值不同而引发更多环流,要保证任意时刻上下桥臂投入的电抗值之和为恒定值;②上下桥臂投入电抗值之差可以随工况变化而改变。由此设计了如图2所示的控制策略。

图2 电抗子模块分段投切方案控制流程图Fig.2 Flow chart of dynamic switching control for LSM

上下桥臂投入子模块个数之和为N。当上桥臂投入MMC子模块个数Nup

(26)

式中：nl为每桥臂上所有的电抗子模块数目;nlref为根据不同工况设置的上、下桥臂投入电抗子模块个数之差参考值。

当Nup>N/2时,上桥臂等效电容较小,令

(27)

而下桥臂投入的电抗子模块个数nldown取：

nldown=nl-nlup

(28)

可以看出,上下桥臂接入的电抗子模块个数之和始终为nl,即任意时刻一相的总电抗值维持nlL0不变;之差为nlref,可以根据工况需要设置。此时可以满足上文中对控制策略的要求。

nlref决定了式(22)中L1的大小,即L1=nlref·L0。实际控制中,应根据系统流过桥臂电流较小时的工况(一般为换流站工作在逆变状态、非满功率运行时)设置最大的nlref,此时nlref=nl。其他工况下的nlref应相应减小,以使桥臂电流不会超过器件额定值。

得到上下桥臂各投入的电抗子模块个数后,按照一定频率(可按nlup是否变化作为是否改变信号的依据)生成各个电抗子模块内IGBT的控制信号。为避免桥臂电抗器突然接入主电路引起过电压,应该保证电抗子模块投入时桥臂流过的电流值较小。值得注意的是,判断是否要投入电抗的时刻为桥臂投入子模块数为N/2时,正是调制电压的过零点,通过计算此时桥臂电流与调制电压的相位差,桥臂电流过零点是可以预测的。可在预测的基础上,在IGBT关断信号的产生中增加判断逻辑,通过测量桥臂电流,仅在桥臂电流小于一定限值时才允许IGBT关断,投入电抗子模块。该限值应综合考虑过电压承受能力和测量时延。

如图1所示,对于任一电抗子模块,其电抗器上反向并联的两个IGBT接收导通信号时,IGBT支路短路,电抗子模块被切除;同时接收关断信号时,IGBT支路断开,电抗子模块接入桥臂。则控制环节应发出2nl组信号,令上桥臂的电抗子模块中nlup对IGBT关断,nl-nlup对IGBT导通;下桥臂的电抗子模块中nldown对IGBT关断,nl-nldown对IGBT导通。

值得注意的是,从交流侧向换流器看时,上下桥臂电抗对外等效为并联,由于任意时刻都存在一个桥臂的电抗值较小,并联电抗值比不采用方案的MMC更小,不会使换流器的动态性能变差。

3 仿真分析

3.1 仿真模型

在PSCAD/EMTDC环境下搭建了双端MMC半桥HVDC仿真模型。两端换流器均为三相六臂MMC,系统详细参数如附录A表A1所示,两端换流站子模块个数均为216(不含冗余),子模块电容容值C=5 000 μF,控制方式为换流站C1定Udc=640 kV,定Q=0 Mvar;换流站C2定P=1 000 MW,定Q=0 Mvar。

将电抗子模块方案及环流抑制控制方案与未采用任何方案的MMC系统进行对比分析。三种情况下桥臂上所接电抗器总和均为0.150 1 H。

对于电抗器投切方案,取灵活可变部分电抗值为 0.15 H,接入的电抗子模块个数为上、下桥臂各10个,即nl=10,每个电抗子模块中所接电感为0.015 H。为尽可能发挥方案作用,应使电抗子模块内IGBT的有较强的通流能力。所选IGBT型号为5SNA 1500E330305,参数为3.3 kV/1.5 kA,厂商为ABB。当换流器工作在逆变运行状态下,传输1 000 MW额定功率时,为控制桥臂电流在器件承受范围内,取nlref=8。

3.2 电抗子模块分段投切方案仿真结果

为体现电抗子模块分段投切方案的降容效果,图3为在4.5 s(稳态运行阶段)投入电抗子模块分段投切方案前后部分参数的波形。在4.5 s前,电抗子模块中IGBT均处于闭锁状态,即电抗器全部投入。4.5 s时启动电抗子模块控制,开始投切电抗。图3(a)为方案投入前后a相上桥臂子模块电容电压的波形,可以看出电抗子模块的分段投切使电容电压波动水平明显降低。由于各子模块运行状态一致,其他桥臂子模块电压也同样明显降低。图3(b)为控制投入前后a相上桥臂的桥臂电流波形变化,桥臂电流正向有效值增大,负向有效值减小,因此一个周期内电流有效值变化不大,仍保持在器件允许范围内。

图3 电抗子模块投切方案投入前后波形对比Fig.3 Comparison of arm current waveforms with and without using switching scheme for LSM

但在电抗子模块方案的实际应用中,应在系统启动阶段就开始方案的投切控制,从而保证稳态运行阶段下任意时刻一相的总电抗值维持恒定。图4(a)和(b)分别为在系统有功功率抬升阶段(3.5 s)投入电抗子模块方案时与不采用降容方案下的有功功率和无功功率波形对比。采用电抗投切控制方案时功率仍能跟随控制参考值,表明方案不会影响系统运行。

图4 电抗子模块投切方案下功率波形对比Fig.4 Comparison of power waveforms with using switching scheme for LSM

3.3 电抗子模块投切方案与环流抑制控制方案仿真对比

图5(a)至(c)分别为当传输功率同为1 000 MW的情况下,不采用任何抑制方案、采用环流抑制控制方案、采用电抗子模块投切方案时a相上桥臂子模块的电容电压波形。如图5(b)所示,环流抑制控制方案可以将电容电压波动的波峰波谷差值降低24.6%。如图5(c)所示,电抗子模块分段投切方案可将电容电压波动的峰谷差降低36.3%。

图6为三种方案投入前后子模块电容电压中各次交流分量的频谱图,体现了对子模块电压的各次分量的抑制情况,由于4次及更高次分量占比较小,在此只列出1,2,3次分量的幅值。由图6可以看出,桥臂电抗器分段投切方案对1,2,3次电压波动均有较好的抑制作用,这是因为其电抗投切对于桥臂上各次电流均有影响,从而对各次电压分量都有抑制效果。

图5 各种方案降容效果对比Fig.5 Effect comparison of capacitor voltage suppression

图6 不同方案下的电容电压频谱图Fig.6 Spectrogram of capacitor voltage with different schemes

4 损耗分析

MMC半桥子模块的损耗的主要来源于IGBT、二极管的开关损耗与通态损耗[20],还包含较小的桥臂电抗器损耗。IGBT和二极管的导通损耗的计算公式分别如式(29)和式(30)所示。

PTcon=UCEIC=(RTIC+UCE0)IC

(29)

PDcon=UDID=(RDID+UD0)ID

(30)

式中：UCE为IGBT集电极和发射极之间的电压;IC和ID分别为IGBT与二极管的工作电流;RT和RD分别为IGBT与二极管的导通电阻,与结温有关;UCE0和UD0分别为IGBT和二极管的通态压降,与结温有关。为简化计算并保证一定裕量,可默认结温为125 ℃[21]。

IGBT和二极管的开关损耗计算公式如下[21]：

(31)

(32)

(33)

式中：a1,b1,c1,a2,b2,c2,a3,b3,c3为拟合系数;Eon为IGBT单次开通消耗的能量;Eoff为IGBT单次关断消耗的能量;EDrec为二极管单次反向恢复消耗的能量。

对于附加的电抗子模块,其所选IGBT型号为5SNA 1500E330305,与MMC子模块相同。对于IGBT和二极管,由附录A表A2和表A3中的IGBT模块在结温125 ℃时的参数,可通过式(29)至式(33)计算得出通态损耗与开关损耗。

电抗子模块与桥臂串联,导通时流过电流即为桥臂电流。对于一相上桥臂的电抗子模块,半周期内有(nl+nlref)/2个IGBT和(nl+nlref)/2个二极管导通,另外半周期有(nl-nlref)/2个IGBT和二极管导通;每周期电抗子模块各器件最多开断一次。

电抗器的损耗为直流损耗和总谐波电流损耗之和[22]。计算公式分别如式(34)和式(35)所示。

P1=Id2R

(34)

(35)

式中：Id为电抗器流过直流电流;Iv通过电抗器的v次谐波电流有效值;R为直流电阻;Xv为v次谐波下电抗值;Qv为对应谐波下电抗器的品质因数。取基波下品质因数Q1=400,直流电阻R=0.1 Ω。

根据文献[21]中所提方法计算得出的单端MMC的损耗功率如附录A图A2所示。图A2中,电抗子模块分段投切方案下MMC子模块的通态损耗为3.196 5 MW,电抗子模块器件通态损耗为0.24 MW;MMC子模块开关损耗为3.59 MW,电抗子模块开关损耗0.013 MW;桥臂电抗器损耗0.185 MW;电抗子模块新增器件损耗为0.253 MW,占换流器总损耗的3.502%,占传输功率的0.025 3%。

5 结语

为降低MMC换流站电容值,本文对子模块电容电压波动的抑制方法进行了研究。首先分析了考虑2次和4次环流分量的MMC子模块电压波动产生机理,得出桥臂电流与电容电压相互影响的关系。从桥臂电抗出发,提出了以子模块形式分段投切桥臂电抗器的降容方法,通过改变上下桥臂间电流分布来抑制电容电压波动。

在PSCAD/EMTDC环境下进行了仿真验证。结果表明,方案能有效抑制子模块电容电压的波动,且由于不针对某一确定频率的环流分量,可以对各次子模块电容电压波动均有较好的抑制效果。

采用电抗子模块分段投切的MMC降容方法,由于对原有换流器拓扑进行了修改,在应用上存在一定障碍。但拓扑方案与部分控制器方案不冲突,与目前已经较为成熟的控制类降容方案的结合使用有一定的研究意义,但方案间的配合仍需进一步研究;由于电抗子模块增加了器件使用,使成本和损耗有所上升,应结合降容效果综合考虑参数设置,对此有待进一步研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。