电力系统发电侧和负荷侧共同碳责任分摊方法

陈丽霞， 孙 弢， 周 云， Ella ZHOU， 方 陈， 冯冬涵

(1. 电力传输与功率变换控制教育部重点实验室(上海交通大学)， 上海市 200240； 2. 美国国家可再生能源实验室， 戈尔登 80401， 美国； 3． 国网上海市电力公司电力科学研究院， 上海市 200437)

0 引言

全球气候变暖是当前人类社会面临的巨大挑战之一，电力行业作为化石燃料消耗的主要行业，占能源消耗相关碳排放总量的近40%[1]。低碳化对于电力行业是一个艰巨的任务，电力行业目前正在从各方面寻找符合自身特点的低碳化道路[2-4]。因此，开展电力系统碳责任(即统计时间内全系统的碳排放总量)在各利益主体间的分摊研究具有重要意义。

由于碳排放和发电环节直接相关，因此传统的对于电力系统碳责任的相关研究侧重在发电侧“看得见”的碳排放，主要有宏观统计方法和全寿命周期的方法[5-7]。但这类方法只能分析发电侧碳排放量的大小，而无法考虑电力系统的网络结构和传输特性。相应地，世界各国也针对发电侧制定了许多减排政策，如总量管制和交易制度、上网电价补贴政策、碳税等，这些政策在实际实施过程中遇到了诸多问题与挑战。

近年来随着智能电网的发展，需求侧响应对于电力系统的节能减排起到了重要作用。有越来越多的学者将电力系统碳责任分摊研究从发电侧转移到了负荷侧。其中，基于碳排放流理论[8-10]的负荷侧碳责任分摊得到了广泛应用和研究。文献[11]基于碳排放流理论，提出了一种以交易为分配主体的计算模型，用于计算负荷产生的碳排放。文献[12]通过负荷分析对碳排放结构进行分解，得出了在忽略发电机组承担网损对应的碳排放量的情况下，负荷所承担的碳排放流量基本等于系统所有机组所注入的碳排放流量。除了基于碳排放流理论的负荷侧碳责任分摊研究，文献[13]采用了碳流追踪的方法对负荷侧的碳责任分摊进行研究；文献[14]从合作博弈的角度，采用合作博弈理论中经典解的概念将碳责任在负荷侧进行分摊；文献[15]基于图论的知识研究了碳责任在负荷侧的分摊。

目前已有的文献几乎没有涉及发电侧和负荷侧共同分摊碳责任的相关研究。仅在发电侧分摊碳责任对负荷成员没有直接的激励信号；同样地，仅在负荷侧分摊碳责任不会直接对发电机组产生激励。此外，对于电力系统，发电机组和负荷是相互依存的关系，缺少其中的任何一方都不会产生发电行为，并且发电机组和负荷都具有节能减排的潜力，仅在单一侧进行碳责任的分摊也是不公平的。因此，本文认为两者都应该承担起电力系统节能减排的责任。

本文基于合作博弈理论，将发电侧与负荷侧共同碳责任分摊问题建模成一个基于合作博弈的成本分摊问题。同时采用发电侧和负荷侧各承担一半系统碳责任的原则，在双边竞价电力市场模式下，选用Aumann-Shapley法对发电侧与负荷侧共同碳责任分摊进行具体求解。最后基于算例分析探究双侧碳责任分摊机制的有效性和分摊结果的合理性。

1 发电侧与负荷侧共同碳责任分摊及其建模

基于双边竞价的电力市场出清模型如式(1)所示。

(1)

对于发电侧和负荷侧共同碳责任分摊问题，本文基于双边竞价的电力市场模式，发电机组和负荷均参与市场报价，市场出清结果通过求解以社会效益最大化为目标的优化模型得出。

在电力系统中，发电机组和负荷在能源和碳责任方面是相互依存的关系，缺少其中的任何一方，系统都不会产生发电行为，发电侧和负荷侧对电力系统有着同等重要的作用，它们也应承担起同等大小的电力系统节能减排的责任。因此，对于碳责任在发电侧和负荷侧的共同分摊，本文采用发电侧和负荷侧各承担一半系统碳责任的原则，并在此基础上进行碳责任在发电机组和负荷间的分摊。

合作博弈作为解决成本分摊问题的有力工具，在电力系统成本分摊领域有着广泛的应用，如传输成本分摊、线路损耗分摊、机组启停成本分摊等[16-18]。本文将发电侧和负荷侧共同碳责任分摊问题建模成一个基于合作博弈的成本分摊问题。典型的合作博弈问题可以用(N,c)表示，其中N表示所有参与成员构成的集合，对应全联盟，c(·)表示合作博弈问题对应的特征函数。具体地，在本文的模型中，求解碳责任在负荷侧的分摊时，参与成员为所有负荷成员；求解碳责任在发电侧的分摊时，参与成员为所有发电机组。特征函数为系统碳排放量的计算，c(N)表示全联盟对应系统产生的总碳排放量，用S表示子联盟，即N的非空真子集(S⊆N)，c(S)表示有且只有S中的成员存在于系统中时对应的系统碳排放量，相应地有c(∅)=0。

2 基于Aumann-Shapley法的碳责任分摊

Shapley值是合作博弈中重要经典解的概念之一，它体现了成员对各个子联盟的平均边际贡献。但Shapley值的计算复杂度随参与成员数目的增加呈指数型上涨，且分摊结果容易受到参与成员自身相对大小的影响而缺乏一定的公平性。Aumann-Shapley法作为Shapley值法在参与成员无穷多情况下的一种延拓，克服了Shapley值法的上述缺陷，并满足有效性、虚拟性和可加性的公理化标准[19]，在电力系统阻塞费用分摊、传输费用分摊、网损分摊等问题中具有广泛应用[20-22]。文献[20]研究了基于Aumann-Shapley法的传输费用在发电机组和负荷之间的分摊；文献[21]研究了基于Aumann-Shapley法的阻塞费用分摊；文献[22]将Aumann-Shapley法应用于有功和无功网损分摊问题。

本文将Aumann-Shapley法应用于发电侧和负荷侧共同碳责任分摊。Aumann-Shapley法的计算采用积分的形式，参与成员n(0≤n≤NG+ND)基于Aumann-Shapley法分摊到的碳责任是其实际功率从0到Pn的积分，如下式所示：

(2)

式中：t为积分变量；P为系统参与成员构成的功率向量；c(tP)为系统碳排放的计算函数，系统碳排放的计算详见附录A；Pn为成员n的实际功率。

(3)

在电力系统中，系统碳排放的计算并非是一个连续可微的函数，因此计算求解的过程需要进行离散处理来代替式(2)中的精确解。基于离散处理，成员n基于Aumann-Shapley法分摊到的碳责任为：

(4)

式中：M表示将参与成员的功率平均分成M个离散段；ΔPn为成员n的功率微增量；[c(kP/M+ΔPn)-c(kP/M)]/ΔPn表示在第k个离散段，成员n对系统碳排放的单位边际贡献量。

参与成员n基于Aumann-Shapley法分摊到的碳责任结果体现了其对于系统实际碳排放的平均边际贡献。值得说明的是，在该方法下，对于水电机组等可再生能源，其对系统实际碳排放的边际贡献为0，分摊到的碳责任也为0，因此，基于Aumann-Shapley法的碳责任分摊实际上保证了发电侧碳责任分摊仅发生于常规火电机组。

3 算例分析

本节算例分析包含两个部分：第1部分在简单PJM 5节点系统中，将碳责任赋予一定的经济效益，以碳成本的形式施加给各参与成员，分别探究碳责任仅在发电侧分摊、仅在负荷侧分摊与在发电侧和负荷侧共同分摊3种情况对各发电机组出力、实际负荷、系统碳排放和社会效益的影响，以此检验双侧分摊机制的可行性；第2部分应用Aumann-Shapley法在IEEE 30节点系统中进行发电侧和负荷侧共同碳责任分摊，分析分摊结果的合理性。

3.1 PJM 5节点系统算例

PJM 5节点系统的网络结构及参数参考文献[23]，机组和负荷信息见附录B表B1和表B2。假设系统中输电线路1-4的容量约束为150 MW，其余输电线路没有容量约束。

对于分摊机制可行性的探究，本文基于分摊结果做出如下处理：基于机组和负荷在一段结算时期内的出力和实际负荷以及系统碳排放情况，进行碳责任在参与成员之间的分摊，将各成员分摊到的碳责任在下一结算时期以碳成本的形式施加给它们，机组和负荷基于施加的碳成本进行新的报价，探究基于碳责任分摊结果施加的碳成本对机组出力、实际负荷和系统碳排放的影响。具体地，单位功率碳责任分摊结果乘以碳价构成边际碳成本，本文假设碳价为32美元/t。机组新报价为初始报价加上边际碳成本，负荷新报价为初始报价减去边际碳成本。以机组为例，假设出力为100 MW的机组初始报价为30美元/(MW·h)，分摊到的碳责任为50 t/h，则其分摊到的单位功率碳责任为0.5 t/(MW·h)，边际碳成本为0.5 t/(MW·h)×32美元/t=16美元/(MW·h)，故机组的新报价为46美元/(MW·h)。

由于篇幅的限制，本节仅列出基于分摊结果的机组出力和负荷情况对比，对于3种分摊机制下的分摊结果以及机组和负荷基于分摊结果的新报价，见附录B表B3至表B8。

3.1.1发电侧碳责任分摊

对于发电侧碳责任分摊，本部分依据机组对系统的实际碳排放贡献进行分摊，基于发电侧碳责任分摊结果的机组出力和负荷情况如图1所示。

图1 基于发电侧碳责任分摊结果的机组出力和负荷情况对比Fig.1 Comparison of output of generators and loads based on carbon obligation allocation results on generation side

在发电侧施加碳成本导致发电机组报价提高，其中机组G5由于碳排放强度最高，施加碳成本后报价最高，竞争力下降，从而出力降为0，报价次高的机组G3的出力也有所下降。此外，由于机组报价的提高，负荷L1的报价低于机组G3和G5的报价，实际负荷降为0。此时，系统碳排放由原来的405.56 t降到259 t。可见，发电侧碳责任分摊机制对发电机组有直接激励作用，施加碳成本使得高碳排放强度机组的报价上升，竞争力下降，从而促进系统碳排放的降低，对于负荷没有直接激励作用。

3.1.2负荷侧碳责任分摊

对于负荷侧碳责任分摊，本节采用碳流追踪法进行分摊[13]，基于负荷侧碳责任分摊结果的机组出力和负荷情况如图2所示。

图2 基于负荷侧碳责任分摊结果的机组出力和负荷情况对比Fig.2 Comparison of output of generators and loads based on carbon obligation allocation results on load side

在负荷侧施加碳成本使得负荷报价下降，其中，负荷L1的报价最低，负荷降为0，负荷L3的实际负荷值有所下降。而各发电机组的报价保持不变，与机组G3相比，高碳排放强度机组G5的报价较低，仍然有着较高的出力，报价最高的机组G3的出力降为0。此时，系统碳排放由原来的405.56 t降为308.64 t。由此可见，负荷侧碳责任分摊机制对负荷有直接的激励作用，能够激发需求侧响应，促使负荷调整用电需求，但对于发电侧出力结构的改善没有直接的激励作用。

3.1.3发电侧和负荷侧共同碳责任分摊

对于发电侧和负荷侧共同碳责任分摊，采用Aumann-Shapley法进行分摊，基于发电侧和负荷侧共同碳责任分摊结果的机组出力和负荷情况如图3所示。

图3 基于发电侧和负荷侧共同碳责任分摊结果的机组出力和负荷情况对比Fig.3 Comparison of output of generators and loads based on carbon obligation allocation results on both generation side and load side

在负荷侧，施加的碳成本使得负荷报价下降，报价最低的负荷L1实际负荷降为0，报价次低的负荷L2的实际负荷也有所降低。在发电侧，施加的碳成本使得机组报价提高，报价最高的机组G5和G3的出力均降为0。此时，系统碳排放由原来的405.56 t降为220 t。由此可见，发电侧和负荷侧共同碳责任分摊机制对机组和负荷都有着直接的激励作用，在发电侧，能够促进机组出力结构的改善，在负荷侧，能够促使负荷用电需求的调整。

4种情况下系统碳排放和社会效益情况对比如图4所示。其中，社会效益即式(1)中的目标函数值。此外，对于发电侧和负荷侧共同碳责任分摊，本文引入对比方法与Aumann-Shapley法的分摊结果进行对比，由于正文篇幅的限制，详细内容可见附录B表B9、表B10和图B1。

图4 系统碳排放和社会效益情况对比Fig.4 Comparison of carbon emission and social welfare

由图4可知，双侧分摊机制下系统碳排放最低，且与仅在发电侧和仅在负荷侧碳责任分摊机制相比，其社会效益略高于后两者。可见，双侧分摊机制在不牺牲社会效益的情况下，相较于单一侧分摊机制进一步降低了系统碳排放。

根据本节算例结果，本文提出的发电侧和负荷侧共同碳责任分摊机制使得发电侧和负荷侧都承担起电力系统节能减排的责任，对发电机组和负荷都有直接的激励作用，能激励发电机组和负荷的节能降耗行为，且与单一侧分摊机制相比，能够在不牺牲社会效益的情况下降低系统碳排放。可见，在具体的参数条件下，本文所提机制能够更好地激励机组和负荷的节能降耗行为，促进电力系统低碳发展的效果，具有一定的可行性。

3.2 IEEE 30节点系统算例

IEEE 30节点系统网络结构及参数参考文献[24]，机组和负荷信息见附录C表C1和表C2，一日中机组组合情况和日单位负荷曲线见附录C图C1。机组实际碳排放情况以及基于Aumann-Shapley法的分摊结果如表1所示。

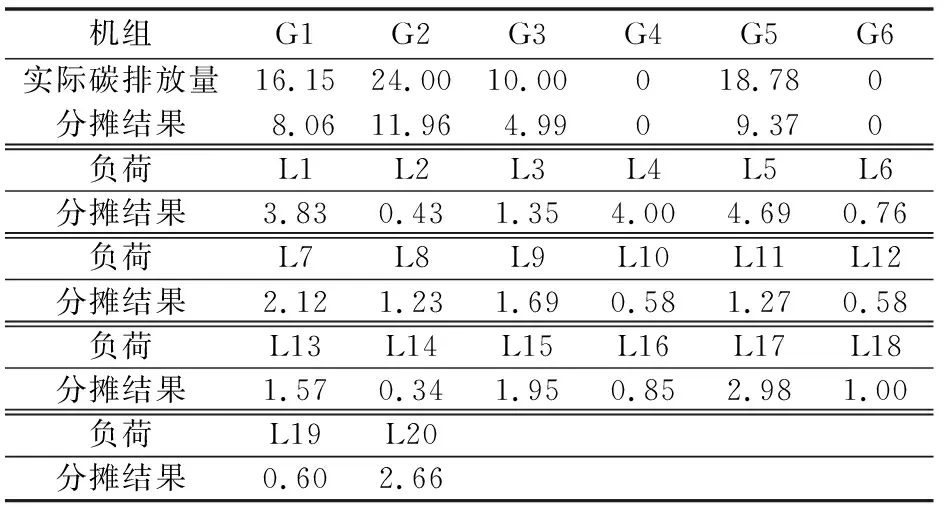
表1 IEEE 30节点系统机组实际碳排放及分摊结果Table 1 Carbon emission of generators and allocation results in IEEE 30-bus system t/h

分析上述分摊结果，对于发电侧，对照表1中机组实际碳排放情况，可见机组分摊到的碳责任比例与其实际对系统的碳排放贡献比例一致，具有合理性。对于负荷侧，基于Aumann-Shapley法的分摊结果综合体现了负荷大小和地理位置因素的影响。具体地，负荷L20的需求比负荷L19大得多，从而负荷L20分摊到了更多的碳责任。而负荷L12和负荷L16虽然大小相同，但由于两者所处地理位置不同，最终分摊到了不同的碳责任。

此外，根据日负荷曲线，进行发电机组和负荷在一日24 h的碳责任分摊，分摊结果见附录C图C2。由图可知，对于发电机组，07:00—08:00时间段内，6台机组都处于开启状态，但由于两个时刻负荷大小不同，各机组分摊到的碳责任也不同。对于某一负荷，各时刻由于机组开停机状态不同，其所分摊到的碳责任也在变化。由此可见，分摊结果能够体现时间因素的影响，对于各参与成员，相同的状态由于在各时刻对系统碳排放影响不同而被分摊到不同的碳责任。

4 结语

本文提出将电力系统碳责任在发电侧和负荷侧进行共同分摊，将其建模成一个基于合作博弈的成本分摊问题，采用Aumann-Shapley法具体进行分摊求解。基于算例分析，得出如下结论。

1)在具体的系统参数下，与仅在发电侧碳责任分摊和仅在负荷侧碳责任分摊机制相比，发电侧与负荷侧共同碳责任分摊机制令发电机组和负荷都承担了电力系统节能减排的责任，能激励发电机组和负荷的节能降耗行为，在不牺牲社会效益的情况下降低系统碳排放，具有一定的可行性。

2)基于Aumann-Shapley法的分摊结果给发电机组和负荷都合理地分摊了一定的碳责任，具体地，其在发电侧的分摊结果与发电机组实际对系统的碳排放贡献相符。在负荷侧的分摊结果能综合体现负荷成员大小以及地理位置因素的影响。

本文对发电侧与负荷侧共同碳责任分摊及双侧分摊机制的可行性进行了初步探究，研究内容可以为低碳背景下电力市场机制的设计提供较为可行的思路参考。后续研究拟在此基础上，对发电机组和负荷基于碳责任分摊结果的策略行为进行研究，以更好地检验基于Aumann-Shapley法的双侧碳责任分摊机制的有效性。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。