求解水电站日负荷优化分配的混合整数非线性规划模型

申建建, 张秀飞， 王 健， 程春田， 李秀峰

(1. 大连理工大学水电与水信息研究所， 辽宁省大连市 116024； 2. 云南电力调度控制中心， 云南省昆明市 650011)

0 引言

水电站日负荷优化分配包括机组组合和机组间的负荷分配两个核心问题，目的是在满足系统负荷需求和复杂调度约束条件下，合理安排各机组的启停方式与出力计划，保障机组安稳、高效、经济运行。众所周知，水电运行存在非常复杂的水力和电力时空耦合关系，特别是对于一些大型水电站，呈现出高维、非线性、离散、非凸等典型特点，使得日负荷优化分配建模及求解面临很大困难[1-3]。

关于水电机组组合和负荷分配问题的研究已有许多理论和实践成果[4-5]，包括动态规划、拉格朗日松弛、智能算法[8-9]、解析式规划[-12]等。其中，动态规划可以求得机组间负荷分配的离散最优解，但随着机组台数和离散精度增大，面临严峻“维数灾”问题；拉格朗日松弛通过引入乘子处理复杂耦合约束，但乘子的微小变动会导致振荡或奇异现象[13-14]，收敛性无法保证；智能算法对目标函数和约束条件的要求较低，但其随机搜索特点使得结果稳定性较差，收敛到全局最优解甚至较好的可行解比较困难，在很大程度上限制了其广泛应用。由于涉及机组启停等整数变量，日负荷分配问题更多地被描述为混合整数规划模型求解，但受限于水电系统非线性特性，求解中需要将非线性因素线性化处理，这势必会影响结果精度，通过分段线性尽管可以减少误差，但会降低求解效率，且不同的线性化方法会产生不同的计算结果，如何进行线性化非常关键。以水电机组出力特性曲线为例，文献[15-16]为避免非线性问题，仅采用一条出力—流量关系曲线或者选用某几个局部最优点代替不同水头的发电曲线，忽略了水头变化，直接影响机组的实际发电效率，应用结果表明最大降低了15%[17。为考虑水头影响，文献[18-20]提出了改进的线性化方法，通过将多条出力—流量关系曲线分段线性转换成一系列一维函数或者利用三角形和网格进行三点插值，确实提高了计算精度，但由于引入大量整数变量严重影响了求解效率，且结果与实际出力曲线的误差仍然难以忽视。

事实上，机组组合和负荷分配是典型的非线性整数优化问题，非线性模型比线性模型更能准确描述该问题。为此，本文从水电调度实际特性出发，提出求解水电站日负荷分配的混合整数非线性规划模型(MINLP)，采用多项式技术，分析并准确描述了水电站日负荷分配涉及的水位—库容曲线、尾水位—出库流量曲线、机组流量特性曲线、发电水头等复杂非线性关系，有效避免了线性简化或假定影响优化结果实用性。以金沙江干流溪洛渡水电站18台机组的负荷分配优化问题为例验证了MINLP模型的有效性。

1 数学模型

1.1 目标函数

水电站日负荷优化分配是以电网下达的负荷需求为控制条件，以总耗水量最小[21]为优化目标，并考虑电站和机组复杂水力和电力运行约束，确定日内最优开停机组合以及各台机组的发电出力计划。

(1)

(2)

(3)

式中：F为耗水量最小目标函数；t,T分别为时段号及其时段总数；Δt为t时段小时数；Qt,wt,st分别为电站在时段t的出库流量、开停机产生的耗水量、弃水流量；i，N分别为机组编号及其总台数；qi,t为机组i在时段t的发电流量；wup,wdown分别为机组开机与停机产生的耗水量；yi,t,xi,t分别表示机组的启动操作与停机操作，详细介绍可见1.2.2节。

1.2 约束条件

1.2.1水库运行约束

1)水量平衡约束

Vt+1=Vt+3 600(It-Qt)Δt

(4)

式中：It为电站在时段t的入库流量；Vt为电站在时段t的库容。

2)水位库容、尾水位泄量关系约束

Zt=fzv(Vt)

(5)

(6)

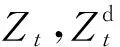
3)边界条件

(7)

(8)

st≥0

(9)

1.2.2机组运行约束

1)负荷平衡约束

(10)

式中：ui,t为机组i在时段t的开停机状态变量(1表示运行，0表示停机)；pi,t为机组i在时段t的出力；Lt为电站在时段t的负荷需求。

2)最小开关机持续时间及开停机次数约束

ui,t-ui,t-1=yi,t-xi,t

(11)

yi,t+xi,t≤1

(12)

(13)

(14)

(15)

3)水头约束

(16)

(17)

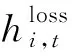
4)限制运行区约束

(18)

(19)

5)水电出力函数

pi,t=fqh(qi,t,hi,t)

(20)

6)边界约束条件

0≤qi,t≤ui,tqi,max

(21)

0≤pi,t≤ui,tpi,max

(22)

式中：qi,max为机组i的最大发电流量。

2 基于多项式技术的MINLP模型

上述模型的复杂性主要体现在水位—库容关系(式(5))、尾水位—出库流量关系(式(6))、水头(式(16)、式(17))以及出力(式(20))等非线性函数，如何合理表述这些非线性因素是构建可求解MINLP模型的关键，因此下文分别针对这些非线性关系详细叙述相应的处理策略。

2.1 水位—库容关系处理策略

水库水位与库容关系是水电机组中典型的非线性函数，在线性规划模型中通常对水位—库容曲线进行线性化或者分段线性，本文通过分析该曲线特征，采用多项式描述水位—库容关系，并且本文在分析多个电站数据基础上发现低阶多项式(小于四阶)在基础数据点较多的情况下拟合精度较低，高阶多项式拟合精度一般较高，但高于四阶时精度改善效果明显变小，且会增加计算量从而降低计算效率，因而本文选用4次多项式拟合，按此方法可将式(5)转换为：

(23)

式中：a0，ai(i=1,2,3,4)分别为常数与四次多项式函数系数(曲线拟合得到)。

结合下文实例中电站的水位—库容曲线进行测试(包含70个离散数据点)，采用MATLAB 2014R进行拟合，拟合后数据与实际数据点的平均误差仅0.000 06%(误差=|拟合值-实际值|/实际值)，确定系数R2及和方差(SSE)分别为0.999 9，0.394 9，表明多项式拟合方法可以精确描述实际的水位—库容曲线。

2.2 尾水位—出库流量关系处理策略

与水位—库容关系类似，尾水位—出库流量曲线也是需要考虑的重要非线性因素，同理采用四次多项式表述二者关系，即将式(6)转换为：

(24)

式中：b0，bi(i=1,2,3,4)分别为常数与四次多项式函数系数。

通过尾水位—出库流量曲线40个离散数据点拟合平均误差为0.06%、确定系数为0.999 5、和方差为2.568，表明采用式(24)可以满足尾水位—出库流量曲线实际精度要求。

2.3 发电水头处理策略

电站发电水头取决于上游水位、尾水位以及机组水头损失，水头损失是机组发电流量的非线性函数，一般采用下式表达：

(25)

式中：ci，ci′分别为水头损失系数与常数。

根据式(23)—式(25)以及式(17)，电站净水头可以等效表述为库容与出库流量的多元四次函数。

2.4 出力特性曲线处理策略

出力特性曲线是表征机组出力与发电流量和水头函数关系的三维曲线簇(见附录A图A1(a))，呈现出明显的非线性特征，如何精确描述是应用数学规划方法求解负荷分配问题的主要难点和关键所在。

在混合整数线性规划(MILP)模型中，分段线性与三角形权值技术是目前常用的两种线性化方法。分段线性是将水头与流量分段离散处理，将机组出力特性曲线简化为不同水头以及不同流量区间的折线段，见附录A图A1(b)；模型中需要引入0-1变量，利用互斥原理确定某一时刻机组水头与发电流量所处区间，线性插值得到机组出力。三角形权值技术是将出力、流量、水头三维变量关系投射到二维平面上，通过对可行域三角剖分，并引入0-1变量确保只有一个三角形被选中，利用相似原理由流量和水头得到三角形三个顶点的权重值，进而线性加权三个顶点值确定电站出力，见附录A图A1(c)。上述两种线性化方法的计算精度与离散区间或剖分三角形个数均呈正比关系，所以精度要求越高，计算效率越低。

事实上，水电机组的出力与水头和流量的非线性函数关系在三维坐标轴体系中是复杂的三维曲面关系，采用上述线性化方法势必会造成精度损失，为精确反映这一关系，本文将出力描述为发电流量与水头的二元非线性函数，具体方法见式(26)，对应的三维曲面如图1所示。

(26)

式中：β0，βi(i=1,2,3,4,5)分别为常数与二元二次函数系数。

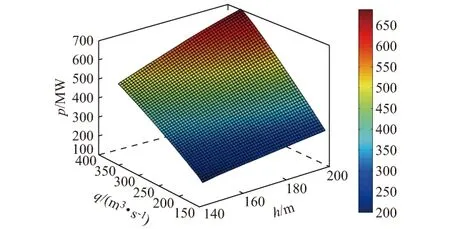
图1 出力特性三维拟合曲面Fig.1 Three-dimensional fitting surface of output characteristics

显然，式(26)无法满足发电流量为0时出力为0这一条件；为此，利用开关机状态变量ui,t，将出力多项式进一步转换为式(27):

(27)

为检验上述出力描述方法的可行性和精度，选用某电站470个水头—流量—出力数据点并通过MATLAB 2014R拟合，平均误差仅0.2%，确定系数为0.997、和方差为1 358，而文献[16]提出的线性拟合方法的平均误差达到9.14%，和方差为18 003.73，确定系数为0.988 2，说明采用二次多项式函数可以更加精确地描述出力特性曲线。

3 实例分析

本文以溪洛渡电站18台机组的日负荷优化分配问题为例验证提出的MINLP模型，并采用LINGO全局最优求解器(Global Slover)进行模型求解。优化计算的硬件环境为：Intel(R)Core(TM)i5-6500 CPU 3.2 GHz,8 GB RAM；软件环境为：Windows 7。需要补充说明，Global Slover可求得凸或非凸MINLP模型的全局最优解[22-23]，主要求解思路为：①以分支定界为核心，通过将可行域不断划分得到一系列子问题；②对子问题进行凸化、线性化来构建一个紧缩的凸包络，以采用成熟线性规划算法求解松弛子问题；③遍历所有子问题(相当于遍历原问题的所有可行域)，求得的最优解即为全局最优解。更为详细的求解原理和流程请参考文献[24]。

为体现MINLP模型的有效性和高效性，本文将其与文献[18]提出的MILP模型进行对比分析，两种模型均采用同等计算条件，主要结合实际需求确定，电站开停机最小持续时间设置为4 h，日内最多开停机次数设置为2次，电站负荷需求参考电网下达计划，溪洛渡机组出力上限为770 MW，最大过流能力为430.5 m3/s，初始水位为570.00 m，限制运行区范围为0～38.7 MW，出力特性曲线拟合系数β0至β5分别为-138.8，-0.364 8，0.010 34，-0.001 675，0.589 3，-0.001 192。在MILP模型中，为提高计算精度与计算效率，根据电站入库流量以及初始条件，预估电站净水头变化范围为190～200 m。基于前述条件，下文从两个方面进行了细致分析：①对比分析不同分段线性数目和分段区间对MILP模型计算效率与结果精度的影响，目的是为后面两种模型比较提供重要条件；②对比分析MINLP与MILP两种模型，包括计算效率和结果精度，重点以机组出力为决策变量，根据实际出力特性曲线、水位—库容曲线、尾水位—出库流量曲线反推机组发电流量和电站总耗水量，在同等条件下比较两种模型的计算结果与实际的偏差大小。

3.1 分段线性数目与分段区间对MILP模型的影响

在MILP模型中，分段区间与分段数目是影响优化结果与计算效率的两个重要因素，本文采用控制变量法，分析了如下两种情况：①在分段区间相同的情况下，分析不同分段数目对计算结果的影响；②在分段数目相同的情况下，分析不同分段区间对计算结果的影响。

MILP模型的求解速度与0-1变量的个数密切相关，由于本文计算规模较大，在较短时间内难以获得全局最优解。笔者发现，当计算时间超过一定时间后(不同计算规模时间不同)，目标函数值维持不变，只是目标函数下界在不断增大，为此本文将前述临界时间对应的优化结果作为MILP模型的优化结果，其有效性已在文献[25]进行了详细论证说明。

1)分段数目的影响

表1列出了水位—库容、尾水位—泄量、出力特性曲线在不同分段数目下的结果，随着分段数量增加，结果精度也越来越高，电站总耗水量呈单调递增趋势，说明对于溪洛渡电站而言，非线性曲线线性分段数量越少，优化结果比实际偏小的幅度越大。

表1 不同分段数目的优化结果Table 1 Optimization results with different numbers of intervals

2)分段区间的影响

选用表1中情景3的分段数目，并控制尾水位—泄量、出力特性曲线的分段区间，通过改变水位—库容曲线分段区间分析对优化结果影响(见附录A表A1)。结果表明，水位—库容曲线的分段区间对结果有较大影响，甚至不合理的分段区间会出现无可行解情况。

可见，MILP模型对非线性因素的线性化方式要求很高，实际应用时需要结合不同问题特点确定适合的线性分段数目、分段区间等重要参数。

3.2 MINLP与MILP两种模型的结果对比

将MINLP模型结果与上述MILP模型得到的精度最高的方案(线性分段数量最多的方案，表1情境1)进行比较分析。另外，考虑到机组数量较多，无法一一列举，下文主要给出了前2台机组的负荷分配结果。

由图2可以看出，MINLP模型与MILP模型结果差异较大，说明选用不同模型会对机组出力安排产生较大影响，主要原因包括两个方面：一是在于模型的特性，两种模型对电站和机组非线性关系的处理方式不同，导致同一时段同一电站出力情况下，即使相同的机组组合和出力分配方式，也会出现不同的耗水量，所以在优化搜索过程中，为尽可能降低发电耗水，两种模型优选得到的机组组合方式可能互不相同；二是MILP模型仅收敛到局部最优解，而MINLP模型收敛到全局最优，不同目标值对应的机组开停机方式和出力过程一般是不同的，甚至存在较大差异，但从日开停机过程来看，两种模型各台机组的开机和停机最小持续时间均满足了给定的约束要求，结果是合理的。从表2可以看出，MILP模型由于对水电站水位—库容、尾水位—泄量、出力—水头—发电流量等非线性关系的线性化处理，引入了大量0-1整数变量，使得模型总变量及约束较MINLP模型增加超过3倍，导致在较短时间内无法求得全局最优解，相反MINLP模型由于0-1变量较少，在349 s内即得到全局最优解，有效体现了MINLP模型的效率优势；而且模型的总耗水量减少703万m3，降幅接近2%，效果也比较明显。

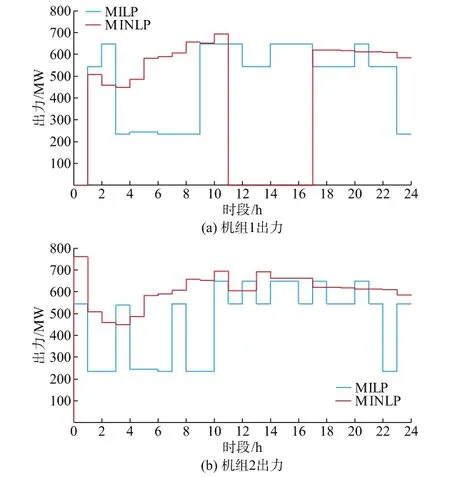
图2 MILP与MINLP模型机组出力过程Fig.2 Generation outputs of units obtained from MILP and MINLP models

由于MINLP与MILP模型对水电非线性关系的处理方式完全不同，仅从目标函数与计算时间上比较两个模型的优劣很难完全反映模型的优越性，因此本文从实际可操作性角度出发做了进一步对比分析。具体思路为：①以两个模型优化得到的机组出力为决策变量，即作为发电决策，反推机组实际发电流量，在推求过程中完全采用电站、机组原始的水位—库容曲线、尾水位—出库流量曲线以及出力特性曲线，其中前两种曲线采用线性插值计算，第三种曲线采用二次线性插值，因为两点线性插值比MINLP模型多项式拟合函数，以及MILP模型的分段线性精度更高；②从机组发电流量出发，将反推的机组流量与模型计算的机组流量进行对比，分析实际误差；③从电站总耗水量出发，对比分析MINLP模型与MILP模型计算结果与实际调度的误差。

由表3可知，两种模型机组发电水量与反推得到的实际调度发电水量都较为接近，说明两种模型的结果精度均比较高。从总耗水量结果看，按照MINLP模型所得机组出力结果指导实际运行时，总耗水量为39 152.71万m3，与模型所得结果39 158.31万m3相差仅5.6万m3，约0.001 43%；MILP模型反推得到的实际调度耗水量为39 925.2万m3，与模型结果39 861.24万m3的误差为63.96万m3，是MINLP模型的11倍，可见采用模型优化结果指导实际生产时，MINLP模型的准确性更高。

表3 机组发电耗水情况Table 3 Water consumption of generation units

通过上述MINLP与MILP模型的综合对比分析，可以得到如下结论。模型应用复杂度方面，MILP模型对非线性因素的线性化方式要求很高，体现在线性分段的数目、分段区间等方面，而且需要预估机组出力特性曲线的水头变化区间，以选取合适的出力计算曲线，否则会对结果造成重大影响，甚至导致不可行解；相比较而言，本文MINLP模型通过拟合多项式函数精确描述非线性关系，降低了人为因素影响，同时由于总变量和总约束数量大幅减少，采用相同条件和相同求解器，MINLP的计算效率较MILP有明显提高，从模型处理的实际操作方式来看，多项式拟合应用更为简捷。计算精度方面，在合理线性化基础上，MILP模型的优化结果可以指导实际生产运行，误差也可以控制在工程允许范围内，但精度要低于MINLP模型；若为提高其计算精度，可以引入更多0-1变量以实现精细化分段，但势必会牺牲模型的计算效率。

4 结语

本文针对水电站复杂非线性关系，建立了以总耗水量最小为目标的水电站日负荷优化分配的混合整数非线性规划模型，并通过溪洛渡电站18台机组的实际检验，获得如下结论。

1)利用多项式拟合方法可以精确描述水电站日负荷分配涉及的非线性函数关系，有效保留水电站实际工程特性。

2)与经典的MILP模型相比，本文MINLP模型由于规避了线性和分段线性化处理，大幅减少了需要优化计算的变量和约束数量，在相同条件下减少了计算耗时，同时基于多项式拟合方法降低了非线性关系线性简化的误差，改善了结果精度，使发电调度决策更能反映机组实际运行情况。

3)以机组出力为决策，通过原始出力特性曲线反推机组实际耗水，发现按照MINLP模型优化结果进行实际调度，精度优于MILP模型，体现了较好的实际可操作性。

4)根据水电站日负荷分配的MINLP和MILP两种模型解决思路和结果对比分析，侧面反映了水电调度中水位、流量、库容、出力等耦合函数关系的处理策略对调度结果的重要性，为以后更好地求解此类问题提供了探索方向。

本文在解决日负荷分配问题时，主要考虑了机组单一限制运行区的情况，部分巨型水电站可能存在多限制运行区且随水头动态变化，这是非常复杂的非线性约束，需要进一步深入研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。