基于改进DSOGI-FLL的并网变流器多谐振解耦网络同步方法

欧阳森, 马文杰, 柯清派

(华南理工大学电力学院, 广东省广州市 510640)

0 引言

当电网电压出现骤升、骤降、三相不平衡、谐波污染等现象时,电网电压幅值和相位信息的准确获取是并网变流器稳定运行的重要保证[1-2]。

在理想电网情况下,对于单同步坐标系软件锁相环(SSRF-SPLL)[3-5],通过控制参数的良好设计,可以获得满意的效果,系统自带的两个积分环节能很好地抑制电网电压中的高次谐波。若电网不平衡,受负序分量影响,其锁相的相位误差增大,以致不能满足并网逆变器的控制需求。为提取基波分量,文献[6]在传统锁相环之前加装低通滤波器,但其存在相角偏移、响应变慢等缺陷。更进一步,文献[7]将离散傅里叶变换与SSRF-SPLL相结合来实现谐波畸变电网下的相位提取。文献[8-9]提出的基于双同步坐标系解耦的软件锁相环(DDSRF-SPLL),具有较高的稳态精度,但是其依赖于相位反馈,因此当电网相位突变时,其过渡过程中存在动态超调大、恢复时间长等问题。文献[10]采用自适应观测器(FRF)来进行电网相位锁定,但是该算法程序计算量较大,比较复杂。文献[11]基于改进型梳状滤波器提出一种可实现频率自适应的锁相环。文献[12]提出用二阶广义积分器(SOGI)产生正交信号来分离电压正、负序分量,同时滤除电网电压中的谐波成分,之后再结合SRF-SPLL进行相角的计算,并提取频率信息作为反馈量实时调整SOGI的谐振频率,该锁相方法不仅能适用于电网电压不平衡情况,同时能适应电网频率突变的情况,但缺点是锁相闭环和频率闭环相互影响以致性能降低。在此基础上,文献[13-14]提出了基于SOGI的锁频环(FLL),该方法的频率自适应依靠SOGI自身结构实现,不再依赖于锁相环的相位反馈,其锁相性能更好,但是当电网畸变严重、低次谐波干扰较大时,系统锁相精度较低。在此基础上,文献[15-16]提出通过多个SOGI并联组成谐振网络的方式来消除电网谐波干扰。类似的,文献[17]基于T/4延时法提出了适用于不平衡及谐波电网下的多谐振解耦锁相环;文献[18]提出了基于多个复系数滤波器并联的解耦网络锁相方法。

综上,本文在文献[15]的研究基础上,在αβ坐标系中进行FLL设计时将负序电压分量考虑在内,以进一步提升双二阶广义积分器锁频环(double second-order generalized integrator frequency-locked loop,DSOGI-FLL)在不平衡电网下的锁频性能。基于前述工作,提出以DSOGI-FLL为基础的多双二阶广义积分器谐振解耦网络的电网同步方法,通过在电网电压畸变、不平衡以及频率偏移的条件下,与单同步坐标系锁相环、双同步坐标系解耦锁相环进行仿真与实验分析,来验证本文所提方法在电网电压畸变或不平衡情况下准确获取电网电压相位和幅值信息的性能。

1 二阶广义积分器锁频环动态特性分析

二阶广义积分器锁频环(SOGI-FLL)的结构参见附录A图A1[15],根据该结构图可以推得SOGI-FLL的状态空间方程如下:

(1)

(2)

(3)

式中:v为输入信号;k为SOGI的阻尼系数;ω′为SOGI的谐振频率;x1和x2为状态变量,对应附录A图A1中相应信号;y为输出矢量;Γ为FLL环路增益;q为90°相位滞后因子,qv′即表示该信号的相位滞后信号v′的角度为90°。

分析式(1)—式(3)可知,SOGI-FLL是一个非线性系统,整个系统的动态响应取决于输入信号的幅值与频率以及参数k和Γ。

当SOGI-FLL在稳态能理想地跟踪输入信号的频率ω0时,有

(4)

此时,式(1)可改写为:

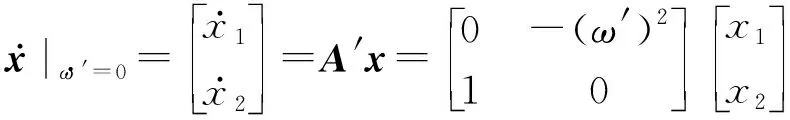
(5)

式(5)中的系统矩阵A′的特征值为实部等于0的纯虚数,因此系统的稳态输出是频率为ω0的谐振轨迹。对于正弦输入,其稳态响应可表示如下:

(6)

当设定SOGI-FLL的谐振频率ω′为某一不等于输入信号频率ω0的常数时,其稳态输出依旧是如式(7)所示的频率为ω0的谐振轨迹。

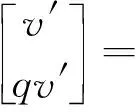
(7)

式中:D(jω)为v到v′的传递函数,其幅频特性如(8)所示[16]。

(8)

根据式(2)和式(7)可知,即使ω′≠ω0,对于状态变量x1恒有如式(9)所示关系:

(9)

因此,由式(1)可得附录A图A1中的误差信号ev为:

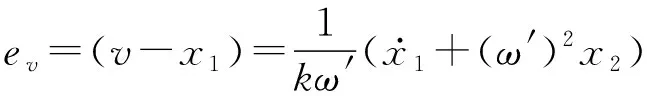
(10)

结合式(9)和式(10)可得反映频率误差的信号ef的稳态响应为:

(11)

考虑到式(11)的高度非线性,为简化分析,在系统接近稳态时,可假设ω′≈ω0,此时有

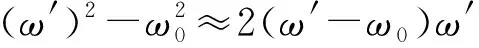
(12)

那么整个系统的动态特性可以描述为:

(13)

当输入信号v=Vsin(ωt+φ)时,可得x2的平方表达式为:

1+cos(2(ωt+φ+∠D(jω0)))

(14)

稳态时,式(14)中的D(jω0)≈1。忽略掉x2中的交流成分,式(13)可简化为:

(15)

式(15)表明了SOGI-FLL的动态响应与输入信号及参数之间的关系,其锁频响应近似为一个一阶系统。

2 DSOGI-FLL动态特性分析

用于三相并网逆变器的DSOGI-FLL结构如图1所示[15]。

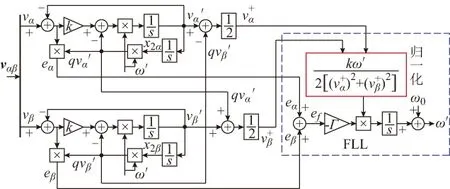
图1 DSOGI-FLL的结构图Fig.1 Structure of DSOGI-FLL

根据图1可知,稳态时α轴、β轴上的频率误差信号eα和eβ为:

(16)

从而在DSOGI-FLL中,反映频率误差的信号ef为:

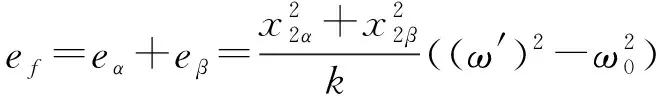
(17)

根据图1所示FLL设计方法,可得DSOGI-FLL的频率动态特性为:

(18)

参照式(12)化简上式得到:

(19)

在电网电压不平衡及畸变情况下,α轴、β轴的输入信号vα和vβ除含有正序基波外,还含有负序基波分量以及谐波分量。对于所含谐波分量,可采用下文第3节中所介绍方法予以消除,因此接下来对DSOGI-FLL所进行的分析只考虑负序分量的影响。从而,vα和vβ可表示如下:

(20)

式中:V+和V-分别为电压正、负序分量幅值;ω0为电网基频;φ-为电压负序分量相角。

(21)

式中:θ+=ω0t;θ-=ω0t-φ-。

根据式(19)和式(21)可得:

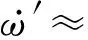
(22)

(23)

分析式(23)可知,当电网电压只含正序分量时,采用图1所示方法,可以消除电压幅值变化的影响,但是当电网不平衡时,DSOGI-FLL的频率响应还与V-相关。因此,为使所设计的FLL的锁频动态特性不受电压正、负序分量的影响,本文设计如图2所示的增益标准化FLL单元。

图2 考虑负序分量的FLL结构Fig.2 Structure of FLL with consideration of negative sequence component

根据图2,DSOGI-FLL系统可简化为附录A图A2所示的一阶线性化频率自适应系统,其响应时间不受电网正、负序电压幅值以及阻尼系数k的影响。

附录A图A2所示系统的传递函数为:

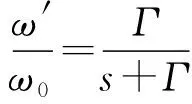
(24)

其调节时间估计值为:

(25)

(26)

(27)

当输入信号为v=Vsin(ω0t)时,结合式(26)和式(27)可得:

(28)

因此,SOGI的稳定时间可由下式估算:

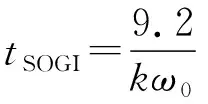
(29)

故在设计DSOGI-FLL参数时需结合式(29)进行。

根据式(23)定义增益标幺值m如下:

(30)

分析附录A图A3可知:①由于在线性化建模分析中,忽略了式(22)中所含二倍频分量,因此,根据B型方案所设计的DSOGI-FLL,其锁频响应曲线与一阶线性模型的阶跃响应曲线相比,存在二倍频波动,但是该一阶线性模型基本可以反映FLL动态响应的平均效应。②当设置参数Γ=100时,根据式(25)计算出的FLL稳定时间估计值为46 ms,由附录A图A3可知,在两种不同的电网不平衡条件下,按B型方案所设计的DSOGI-FLL锁频稳定时间均约为48 ms,与理论模型基本一致。③由于α轴、β轴的SOGI存在过渡过程,从而导致B型FLL在两种条件下的频率响应曲线在动态过程的起始时刻呈现大小不一的波动,约经过20 ms后(与式(29)计算基本相符),两种条件下的频率响应曲线基本趋于一致。④根据附录A图A3(c)可知,采用A型设计方案,在电网不平衡时,由于负序分量的存在,导致增益标幺值m大于1,尤其是在两相故障的情况下m≈2,相当于所设计的控制参数Γ由原来的100变成了200,也即负序分量的存在引起了系统控制参数的偏移,从而导致两种条件下FLL的锁频响应曲线差别较大。当然,这种偏移的大小取决于电网不平衡程度。

综上,本文经理论分析推导出的一阶线性化模型可以较准确地反映DSOGI-FLL的动态响应特性,可用于指导FLL的参数设计;本文所提出的FLL单元增益标准化设计方法可以在较大程度上消除负序分量对FLL锁频动态响应的影响。

3 多DSOGI谐振解耦网络

图3 多DSOGI并联的谐振解耦网络Fig.3 Resonant decoupled network with multiple DSOGIs paralleled

由图3推导出电网基波分量对输入信号的传递函数为:

(31)

式中:D表示D(s),D3表示D3(s),D5表示D5(s),其表达式如式(32)所示。

(32)

根据式(26)和式(31),画出单SOGI和谐振解耦网络的频率特性图如附录A图A4所示。分析该图可知,谐振解耦网络对于频率为3ω′和5ω′的信号成分呈现陷波器特性,因此较之原来的SOGI,其对于电网电压中低次谐波的滤除能力大幅提升,因而在电网畸变情况下其仍能保持良好的锁相精度。在实际应用中可根据需要按照图3原理设置对应频率处的自适应滤波器组成谐振解耦网络以实现电压不平衡及畸变情况下正序基波电压信息的准确获取。

4 仿真与实验分析

4.1 仿真验证

为验证本文所设计多谐振频率解耦网络同步方法的有效性,在PSCAD软件中搭建了单同步坐标系锁相环(Ⅰ型)、双同步坐标系解耦锁相环(Ⅱ型)、基于DSOGI-FLL的多DSOGI谐振解耦网络(Ⅲ型,文献[15]所提方法)、基于改进型DSOGI-FLL的多DSOGI谐振解耦网络(Ⅳ型,本文所提方法)4种锁相环模型进行仿真对比。其中,两种类型DSOGI-FLL中的参数均为k取1.414,Γ取100,且解耦网络中分别为3,5,7次谐波设置了对应的DSOGI自适应滤波器。

仿真条件设定为:①初始50 Hz/60 V(最大值)三相对称电压,在0.2 s时叠加上40 V的负序分量,并且频率跳变为55 Hz;②初始50 Hz/60 V(最大值)三相对称电压,在0.2 s时叠加上25 V的负序分量,并且频率跳变为55 Hz;③初始50 Hz/60 V三相对称电压,在0.2 s时叠加上20 V的3次正序分量,15 V的5次负序分量,7 V的7次正序分量,并且频率跳变为55 Hz。3种条件下所得仿真结果详见附录A图A5至图A7。

根据仿真波形图得出的数据详见附录A表A1,其中,锁频稳定时间以误差不再超过0.2 Hz为标准,分析结果可得出如下结论。

1)在仿真条件①和②下,单同步坐标系锁相环的锁相频率稳态值分别存在11 Hz和3.22 Hz的偏差,d轴定向电压的偏差达40 V;在电压畸变条件下,其锁相性能进一步恶化。

2)两种电压不平衡条件下,双同步坐标系解耦锁相环的锁相频率稳态误差为0.14 Hz,d轴定向电压的偏差为1.45 V;两种类型谐振解耦网络的锁相频率稳态误差仅为0.01 Hz,d轴定向电压的偏差约为0.2 V;由于解耦网络内部存在多个滤波器,结构较复杂,因此其定向电压的动态超调较双同步坐标系解耦锁相环大,锁频稳定速度较慢。

3)在电压畸变条件下,双同步坐标系解耦锁相环的锁相频率稳态误差为2.41 Hz,d轴定向电压的偏差达6.15 V;两种类型谐振解耦网络锁相频率稳态误差仅为0.01 Hz,d轴定向电压的偏差为0.3 V;因此,在电压含较强低次谐波干扰时,谐振解耦网络的检测精度明显优于双同步坐标系解耦锁相环。

4)在3种仿真条件下,Ⅳ型锁相环的锁频稳定时间均约为48 ms,基本一致;反观Ⅲ型锁相环,在条件①和条件②下的锁频稳定时间分别为80 ms和60 ms。表明电网电压中负序分量含量较高时,引起了系统控制参数的偏移,导致FLL与SOGI两部分的动态耦合效应过强,从而导致FLL的稳定时间不减反增,其动态特性不能再用附录A图A2所示的一阶惯性环节来近似,其频率动态响应超调量变大,导致锁频稳定时间变长。

5)分析附录A图A5(f)和图A6(f)可知,在不平衡电网条件下,Ⅳ型锁相环与Ⅲ型锁相环相比,由于Ⅳ型锁相环的锁频动态响应特性几乎不受电压负序分量的影响,因此,其正序基波电压的检测偏差衰减得更快;根据附录A图A7(b)和图A7(f)可知,当电网电压只含谐波分量时,Ⅳ型锁相环与Ⅲ型锁相环的锁相性能几乎一样。

6)在电压三相不平衡或畸变的情况下,Ⅳ型锁相环的稳态锁相频率误差均约为0.01 Hz,能很好地满足并网逆变器的低电压穿越功率控制算法以及孤岛检测对频率检测的要求;3种仿真条件下其锁频稳定时间约为48 ms,这与按式(25)计算的结果基本一致,说明了本文所设计的同步方法的有效性。

4.2 实验验证

为进一步验证本文理论研究的正确性,基于DSP28335平台对本文所提多谐振解耦网络的同步方法进行了实验验证。三相电压数据由模/数转换器(ADC)模块以20 kHz的采样频率获取,分别进行与仿真条件②和③相同的实验验证,实验系统示意图参见附录A图A8。

电压信号由样机产生,锁相环程序编写在该样机的控制器内部,以数组保存程序计算所得数据。实验结果如图4和图5所示。

图4 电压不平衡实验结果Fig.4 Experimental results under unbalanced voltage

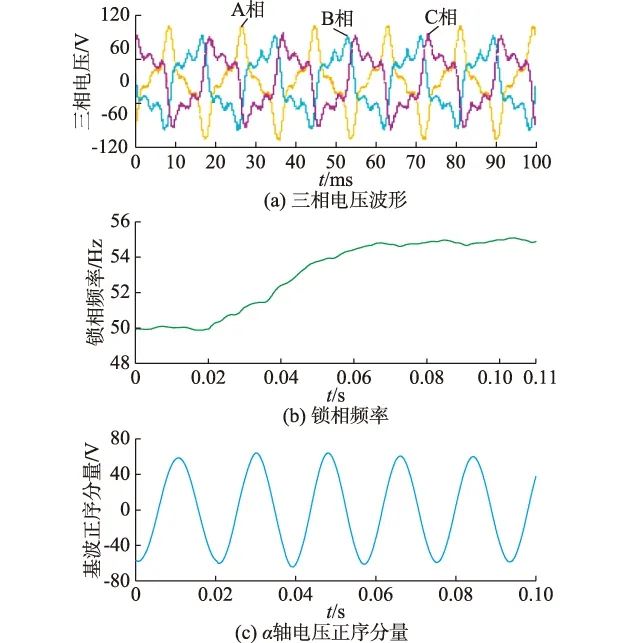
图5 电压畸变实验结果Fig.5 Experimental results under distorted voltage

根据图4和图5可知,在电压不平衡或畸变的情况下,本文所设计的基于改进型DSOGI-FLL的谐振解耦网络的锁相频率响应特性类似于一个一阶惯性环节,其锁频稳定时间均约为50 ms;电压不平衡条件下稳态频率处在54.99～55.06 Hz的波动范围内,电压畸变条件下稳态频率处在54.93～55.07 Hz的波动范围内,两种条件下的稳态频率误差均控制在0.07 Hz内,锁频精度较高。

分析图4(c)和图5(c)可知,当三相电压不平衡时,利用解耦网络所提取出的正序基频分量在稳态时的幅值为59.96 V,负序基频分量幅值为24.96 V;在电压畸变时所提取出的正序基频分量幅值为59.94 V。因此,可见本文所提电网同步方法在电压三相不平衡、畸变的情况下均具有较高的检测精度。

5 结语

为实现电网电压畸变及不平衡情况下电压相位与幅值信息的快速、准确获取,本文以FLL为研究对象,对基于DSOGI-FLL的频率响应状态空间模型展开理论分析,推导出其增益标准化线性模型;根据该模型进行FLL的参数设计,可使系统具有良好的动态响应,且锁频动态性能几乎不受电网基波正、负序电压幅值波动的影响。仿真和实验表明,本文所设计的谐振解耦网络同步方法在电网电压畸变及不平衡情况下仍具有较高的频率检测精度,可适用于孤岛检测等对频率检测要求较高的应用场合。

本文所提同步方法在电网电压不含直流分量的场景下具有较好的检测精度,但当电压信号含有直流分量时会降低FLL的稳态频率检测精度,影响整个解耦网络的频率自适应能力,下一步的研究工作将会纳入该情景。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。