基于相电流有效能量循迹法的配电网单相故障定位
童 宁, 张雪松, 赵 波, 林湘宁, 李正天, 徐 琛
(1. 强电磁工程与新技术国家重点实验室(华中科技大学), 湖北省武汉市 430074;2. 国网浙江省电力有限公司电力科学研究院, 浙江省杭州市 310014)
0 引言
中国6~66 kV配电网属于小电流接地系统。长期以来,其单相接地故障的排查依赖于故障选线及人工巡线,目前相关技术已较为成熟[1-3]。随着智能配电网建设的不断推进,为减少巡线工作量,提高配电网自动化水平,对故障排查精度的要求也同步提高,即实现区段定位甚至故障测距[4-5]。目前工程上较为常用的方法包括首半波法、S注入法[6]和中电阻投切法[7],其中前者受过渡电阻及故障初相角影响较大,准确性较低[8];后两者分别依赖注入信号或中性点并联中值电阻投切过程产生的突变量信号,解决了定位方法从无到有的问题,但有如投资巨大、易使智能设备受间谐波影响、破坏电网原有中性点接地性质等一系列的缺陷。
为解决上述问题,诸多专家及学者进行了丰富的研究。其中,基于遗传算法[9]、专家系统[10]及蚁群算法[11]等智能算法的定位原理容错性较高,但严重依赖于专家经验知识及配电网的拓扑结构[12];基于测距技术的定位原理理论精度较高,但考虑到行波色散现象及复杂折反射过程,其在多分支网络中的应用效果存疑[13-15];基于线路暂态重心频率[16]、同步量测[17]及相电压/电流突变特征[5]的区段定位原理不受上述约束条件限制且能在线进行,但由于零序互感器结构复杂、价格昂贵,且下级分支线路一般不装设电压互感器与同步系统,导致其现阶段工程推广难度较大。事实上,具备良好工程可行性的定位原理应摆脱对零序电流的依赖,充分利用已有的配电自动化系统[18-19],并主动适应目前配电网的低可观性现状。
为此,本文从相电流入手,分析了其对应于故障点上游、下游的分配特性,找出了高频分量在配电网中的一般性分布规律;借助于小波变换定义并提取了故障相电流的有效能量,并根据各级馈线与下级分支线路有效能量比值关系设计了循迹式定位搜索算法;最后基于PSCAD/EMTDC平台搭建了实际配电网模型,仿真模拟了实际故障发生后的有效能量计算及定位搜索过程;计及A/D转换器噪声及配电网参数差异性,验证了所提出的搜索算法在各种严苛场景下的有效性及抗过渡电阻能力。
1 单相故障场景相电流高频特征理论分析
目前典型配电系统中,母线及其直连的出线首端处可测得母线三相电压、母线零序电压、馈线三相电流和零序电流;下级放射状分支线路首端分段开关处装设有分布式终端单元(distribution terminal unit,DTU),采集柱上开关电气量并向配电网控制中心的数据采集与监控(SCADA)系统上报。通常分支线路首端仅装设有两相电流互感器(TA)。

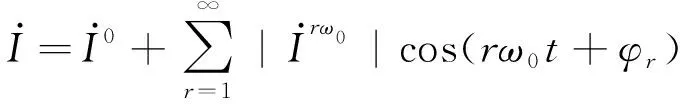
(1)
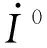


图1 故障分量序网图Fig.1 Sequence network diagram of fault component

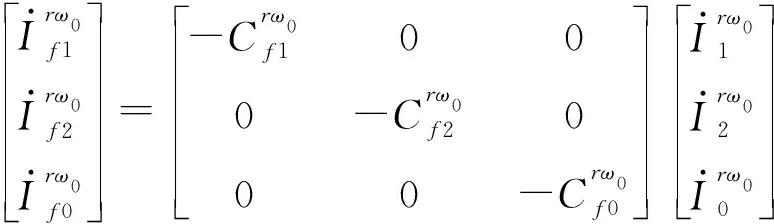
(2)
(3)
在单相接地故障场景下,令接地电流各序分量相等,并视正序与负序电流分布系数一致,可得:
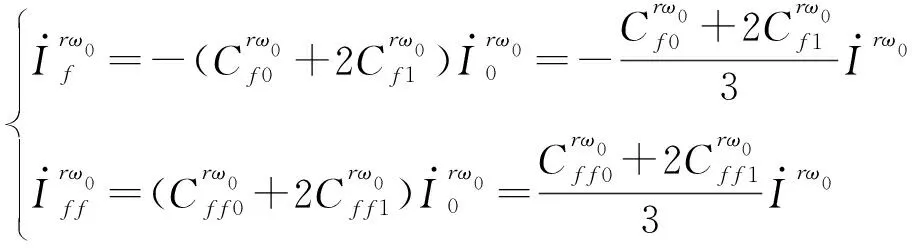
(4)
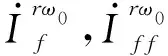
将两者相比可得:

(5)
由基尔霍夫定律可知故障点上下游电流分布系数之和等于实数1,式(5)可写为:

(6)
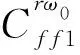

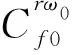
因此在r>R的情况下,对式(6)两边取模值:
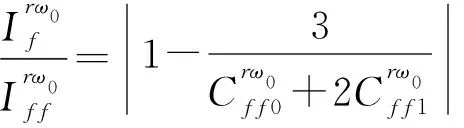
(7)
令两者模值关系满足式(8):
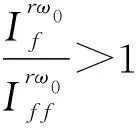
(8)
联立式(7)、式(8)可得:
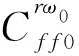
(9)


图2 电流分配系数及相位差Fig.2 Current distribution coefficients and phase error


图3 典型10 kV配电网结构Fig.3 Typical structure of 10 kV distribution network
(10)
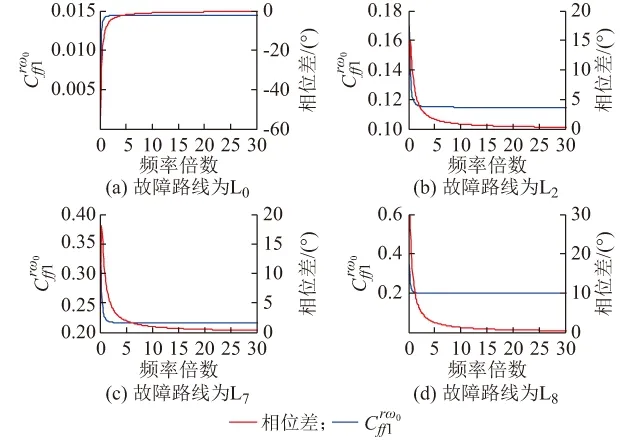
图4 不同故障点下游电流分布系数及相位差Fig.4 Current distribution coefficient and phase difference at different fault points
可根据叠加定理,可知故障点上、下游的全电流为式(10)与正常运行电流的叠加。但正常电流仅为基频分量,其R倍频以上分量为零,故式(10)同样能够表征故障点上、下游故障相全电流的高频分量。取模并整理可得:
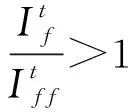
(11)
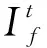
2 基于有效能量的循迹式定位判据
2.1 有效能量提取
小波变换是一种多尺度的信号分析方法,它具有良好的时频域局部化特性,非常适合分析非平稳信号的瞬变特性[25]。基于多分辨率分析理论,离散小波变换(DWT)可通过Mallat算法再现复杂波形的时频域特征。DWT的本质是一组高通/低通滤波器的重复利用,其相关研究成果已较为丰富,在此不再赘述。
单相故障发生后,经过先行的故障诊断及故障选线,故障类型、相别及故障线路信息传送至故障线路及其分支线路上所装设的DTU,告知其保存故障前后三个周期的电流采样数据并进行DWT处理。为克服对时域波形截断而导致的“边缘效应”问题带来的误差,可利用文献[25]采用的方法,通过仅保留故障前后两个周期信号变换结果的方式剔除叠加了“边缘效应”的信号量。考虑到在5倍频以上分量中,电流分布系数与相位差已经能够趋于稳定,同时为消除处于较低频带的正常运行电流、故障分量的低频成分(包括衰减直流分量成分)、单相接地故障时系统内部出现的3次及5次谐波,以确保式(11)的成立,本文将截止频率倍数R设置为6;考虑一般工程中能够达到的20 kHz采样率,可利用DWT对故障相电流进行五层分解,频带分别为A5(0~312.5 Hz),D5(312.5~625 Hz),D4(625~1 250 Hz),D3(1.25~2.5 kHz),D2(2.5~5 kHz),D1(5~10 kHz)。可见忽略A5频带后,即可衰减6倍频以下分量的影响。同时为消除A/D转换器噪声的影响,需忽略D1,D2频带分量。其余频带内小波能量计算方式为:
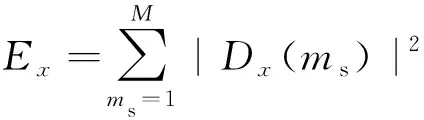
(12)
式中:x=3,4,5;Dx为Dx频带的小波变换结果;M和ms分别为对应频带的抽样点及总变换点数。
定义其余频带能量之和为有效能量,其计算方式为:
(13)
注意到利用式(13)所计算得出的馈线有效能量值与故障方式存在着较大程度的关联性,特别是在故障点距离母线较远,同时发生高阻故障且初相角接近0°时,故障分量非常微弱。为防止误差造成误动,设置如式(14)所示的零序电压启动判据:
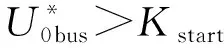
(14)
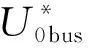

(15)
2.2 基于循迹式判据的故障定位原理
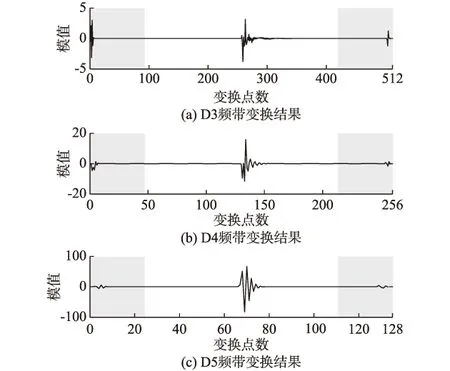
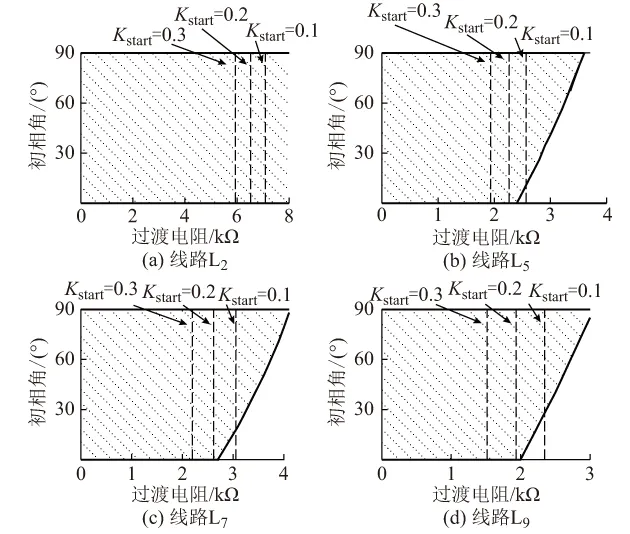
为得出共通性的结论,不妨设馈线分支线路一共有n级(n≥1),其中第1,2,…,m级馈线中均各存在一条处在故障主路径上的线路(1≤m≤n)。假设L0为第一级馈线(故障出线),各级处于主路径的线路分别有KN(N=1,2,…,n)条直连的下级分支线路,这些线路中第jN条落在主路径上。用E表示线路暂态能量,则Ej0为出线L0的暂态能量,则N (16) 当N≥m时,下级线路均不经过主路径,jN不再存在。故可得: EN-1≫Eii=1,2,…,KN (17) 因此构造如下判据实现本文提出的故障定位原理:从选线结果所得出的故障出线开始,依次以本线路首端测得的能量值和所有下级直连分支线路做比较。在N (18) 式中:N=1,2,…,m;Kset为可靠系数,仿照电流保护、距离保护中类似的整定方式,取Kset=1.2躲过TA的20%量测误差。 然后初始化N=1,i=j0,分别代表搜索次数与当前已知的处于故障主路径的第N级馈线。若能量关系满足判据式(18),则重置i与N的值,使之分别为i=jN,N=N+1,开展下一轮搜索并重复检验判据式(18)。当N≥m时,线路首端测得能量值与所有下级直连分支线路之比均大于Kset: (19) 式中:i=1,2,…,KN;N=m+1,m+2,…,n。 一旦判据式(19)成立则立即停止循环,并判断故障点在第N级分支线路上,具体为第N-1级处于故障主路径上的线路所直连的第i条下级分支线路。另外,若某条处于主路径上的线路不存在任何下级分支线路,则故障点搜索将停止于该线路,并确定其为故障线路。需要注意的是,由于故障相别的随机性,在仅装设A,C两相TA的配电网中,一旦单相接地故障发生在B相,且B相未装设TA、无法获取相电流信息,则本文所提出的方法不再适用。综上,循迹式判据定位原理流程如图5所示。 基于PSCAD/EMTDC平台建立图3对应的10 kV配电网模型。设经过先行的故障诊断及故障选线,已确定故障线路为L0,故障相别为A相。架空线及电缆参数分别如附录A表A1、表A2所示。首先设置零序电压启动系数Kstart=0.2。为模拟现场实际工况,根据A/D信噪比计算公式,本文波形中加入了12位A/D在20 kHz采样率下的信噪比为110 dB的噪声信号。考虑到所提出算法对不规则暂态信号的辨识能力的要求,在满足计算精度的同时尽可能地提高计算速度,DWT采用正交紧支撑的db5小波。 图5 故障定位原理流程图Fig.5 Flow chart of fault location principle 根据网络拓扑结构可知总共存在四级馈线,故n=4。根据所述原理,算法首先展开第一轮搜索,N初始化为1。此时K1=3,表示第一轮搜索范围为线路L0及其下游的3条直连馈线,此时DTU记录下附录B图B1中所示馈线L1至L3的A相电流波形。以M0为例,D3,D4,D5频带的变换结果如图6所示,其中阴影部分表示被剔除的数据,可见文献[25]的方法能够有效消除“边缘效应”所带来的误差。 有效能量计算结果及后续循迹过程如附录C图C1所示。其中,第一轮搜索围绕着初级馈线L0及其下级馈线L1,L2,L3展开,其对应的能量编号为Ej0,E1,E2及E3,其中仅有Ej0/E2=0.72,满足判据式(18),表示第二条直连下级馈线处于故障主路径上,将馈线L2能量编号初始化为Ej1,并将N值重置为2;第二轮搜索包含次级馈线L2及其下级馈线L6,L7,其中有且仅有Ej1/E2=0.99,满足判据式(18),表明与其直连的第二条下级馈线处于主路径,将L7编号重置为Ej2,此时N=3;第三轮搜索对象为L7及其下级分支线路L8,L9,可得Ej2/E1=94.49,Ej2/E2=58.99,满足判据式(19),算法停止。此时N值依然为3,代表故障馈线为第三级分支线路,所在分支为L2的第二条分支线路L7。非主路径上的线路与上级线路的有效能量比值结果远远大于1.2的门槛值,保障了判据的灵敏性。 图6 M0处故障相电流D3至D5频带DWT结果Fig.6 DWT results from band D3 to D5 for the fault phase current at M0 可见,经第一轮、第二轮搜索分别确定L1,L5处于故障主路径上,即可确定故障线路为L5。但是,由于过渡电阻较高、故障距离母线较远、故障初相角很小,考虑噪声影响,部分搜索结果已接近1.2的门槛值。其中在第一轮搜索中,上级馈线与L2的有效能量比已达到1.23;在第二轮搜索中,馈线L1与馈线L5的有效能量比值已达1.19。继续增加过渡电阻至2.3 kΩ时,虽然仍然能够得到正确的结论,但零序电压判据已处于临界启动状态。若进一步提高过渡电阻,则L1将在误差影响下被误判为故障线路;幸运的是,此时母线零序电压已低于启动门槛,循迹法搜索过程不会启动。 改变故障点、过渡电阻、初相角以及消弧线圈消谐度,以100 Ω为步长进行仿真遍历,综合考核原理的抗过渡电阻能力及定位准确率。以线路L2,L5,L7,L9为例,其判别性能如图7所示。 图7 不同位置故障时循迹法性能分析Fig.7 Performance of trajectory method under different fault point conditions 其中,阴影部分表示循迹法能够正确动作识别故障区段的工况,虚线表示不同的Kstart取值情况。可见,随着故障点不断远离母线以及初相角的降低,循迹法能够正确判断的范围逐渐减小。对于线路L2而言,8 kΩ以内过渡电阻的单相接地故障均能够被有效识别,且能够覆盖初相角从0°至90°的所有工况。在此范围内,Kstart的降低有利于提高抗过渡电阻能力;但是另一方面,在其余线路上,若Kstart取值过小(Kstart=0.1),则在部分故障程度非常轻微的高阻故障场景下将失去选择性;若Kstart取值过大(Kstart=0.3),则会过分损失抗高阻故障能力。综上所述,取Kstart=0.2能够在最大程度保障选择性的前提下尽可能地提高抗过渡电阻能力,即使在初相角为0°的最不利的工况下,也能够准确识别千欧级的高阻故障。 假设与母线距离最近的线路L0至L3进行了电缆化改造,其余线路仍然为架空线路。直接考虑最严苛场景,即L5末端A相经2 kΩ高阻接地、故障初相角为0°,保持消谐度为8%。母线零序电压、各馈线故障相电流波形及有效能量见附录B图B3。站内SCADA系统接收到的所有馈线故障相电流有效能量大小及循迹过程如附录C图C3所示。 可见在此工况下,循迹法仍然能够有效应对千欧级的高阻故障。注意到与附录C图C2相比,上级线路与主路径上的下级线路有效能量比值能够更可靠地小于整定值,判据反而更灵敏,这是由于本文假定靠近母线的线路被优先进行了电缆化改造。由于电缆线路的对地电容大于架空线路,导致零序网络中故障点上游流过更高幅值的高频零序电流,而正序、负序故障分量网络中的高频电流分配关系基本保持不变。即使电缆线路在配电网中无序分布,也能够通过设置合理的零序电压启动系数Kstart躲过循迹法定位错误的场景,以牺牲一定的灵敏度为代价获取故障定位结果的良好选择性。 本文提出了一种基于有效能量循迹法的配电网定位原理,旨在摆脱传统方法对零序电流、相电压及高成本设备的依赖,提供一种无需高额硬件投资、能够利用现有配电自动化系统实现单相接地故障在线快速定位的方法。 1)放射状配电网中,由于故障点上、下游各序分量等效网络的频率—阻抗关系,导致单相故障发生后,故障点上游故障相电流的高频分量能够显著大于下游及各非主路径的分支线路。 2)利用上述现象构造的循迹式故障定位判据能够适应各种故障位置、过渡电阻、消弧线圈投入状态及初相角工况,其抗过渡电阻能力能够达到千欧级,且能够适应架空线—电缆混联网络。 3)考虑到故障的随机性,为保障在过渡电阻增加、故障分量相对微弱场景下的判断正确性,本文设置了零序电压启动门槛,损失了一部分高阻接地故障下本应具有的灵敏性。如何采用自适应相电流分解及有效能量计算方法,以期达到更高的抗过渡电阻能力,是下一步研究的方向之一。 感谢国网浙江省电力公司科技项目(5211DS16001V)对本文工作的支持。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。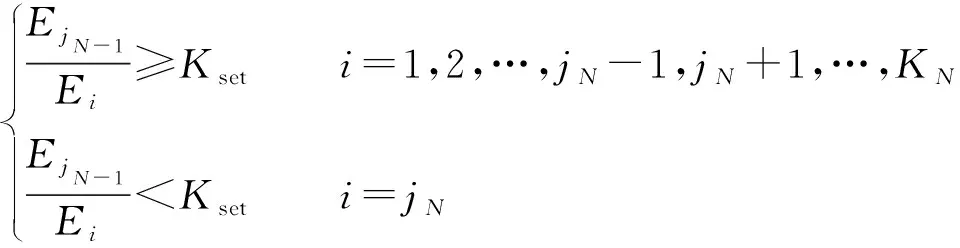
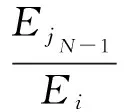
3 仿真验证

3.1 故障特征明显场景下循迹法性能分析
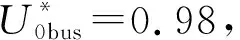
3.2 故障特征不明显场景下循迹法性能分析
3.3 循迹法抗过渡电阻能力分析
3.4 架空线—电缆混联网络适应性分析
4 结语

