基于核函数的高维离散数据聚类算法研究与应用
叶福兰
(福州外语外贸学院理工学院,福州 350202)
0 前言
伴随着互联网技术的飞速发展,我们迎来了大数据时代,生活的各个领域积累了大量有价值的数据信息,这些数据的规模越来越大,维度越来越高,复杂度也越来越强。如何对这些高维数据进行高效分析,挖掘潜在的、有价值的信息是值得研究的一个重要课题。聚类分析作为一种无监督的机器学习方法,是目前最为常用的挖掘数据信息的方法之一,旨在从大量的数据中获取潜在的、有价值的、未知的信息。传统的聚类算法常用于连续型数据的研究,对样本未进行优化,无法达到高精度的聚类效果。作为一种主流的统计学习方法,核学习是解决许多统计学习问题的有力工具,核函数的引入可以将非线性问题转化为线性问题,从而得到准确挖掘。
1 聚类分析[1]
聚类分析是将数据样本按照其特征分成不同的簇(类),使得相同簇之间的对象具有较大的相似性,而不同簇之间的对象具有较大的差异性。主要的聚类分析方法有:基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法及基于模型的方法。主要的基于划分的方法有k-Means算法和k-Medoids算法;基于层次的聚类方法有凝聚法和分裂法;具有代表性的基于密度的算法有DBSCAN算法和OPTICS算法;基于网格的方法将空间对象转化成有限的单元,形成网格结构,如STING算法、WaveCluster算法以及CLIQUE算法等;基于模型的方法试图找到数据样本与某统计模型的最优拟合,如:COBWEB算法、EM算法等。
聚类分析方法通常通过计算距离来衡量数据之间的相似度,距离值越小表示两个数据对象相似性越大,反之差异越大,常用的距离计算方法有(设有两个n维向量x(x1,x2,…,xn),y(y1,y2,…,yn)):
(1)
(2)
(3)
还有曼哈顿距离、马氏距离等。
2 高维数据聚类分析
高维数据存在稀疏性的特点,随着数据维度的增加,使用传统的聚类算法进行分析后得到的结果误差越来越大,影响聚类效果。为了解决维度灾难所带来的问题,目前针对高维数据的聚类方法主要有基于联合的聚类、基于超图的聚类、基于子空间的聚类、基于降维的聚类,而基于子空间和基于降维的聚类居多。基于子空间的聚类是从样本数据中选取多个不同的子集,分别针对子集对应的子空间进行聚类,将聚类局部化在相关维中进行,可以分为硬子空间算法(如PROCLUS算法)和软子空间算法(如WFCM算法)。基于降维的聚类是处理高维数据的一个重要手段,通过将原始高维数据转换为低维空间,对低维空间数据进行聚类,再将聚类结果扩展到原高维空间中,分为线性降维和非线性降维。线性降维要求数据集的特征属性是线性的,对于非线性结构数据集要求采用非线性降维方法解决问题。非线性降维典型算法有:KPCA算法,MDS算法,Isomap算法等。
3 核函数[2]
核函数是一种测量数据样本相似度的重要方法,将核函数引入到聚类分析中,使得原有的高维线性非线性可分的空间映射到线性可分的假设特征空间中,在低维空间计算表现高维空间的分类效果,在输入空间与特征空间中建立起了一座桥梁,有效解决非线性和维度灾难问题。核函数定义如下:
对任意的xi∈Rn(Rn为输入空间,i=1,2,…,n),φ函数是从Rn到高维特征空间H的映射,若存在函数k(xi,xj)=φ(xi)φ(xj)(φ(xi)φ(xj)为xi,xj映射到特征空间上的内积),则称k(xi,xj)为核函数。常见的核函数有:线性核函数、多项式核函数、径向基核函数RBF、Sigmoid核函数、傅里叶核函数等。
1)线性核:k(xi,xj)=(xi,xj),
(4)
2)多项式核:k(xi,xj)= ((xi•xj)+1)d,
(5)
(6)
4)感知器核:k(xi,xj)=tanh(k(xi,xj)+ν),
(7)
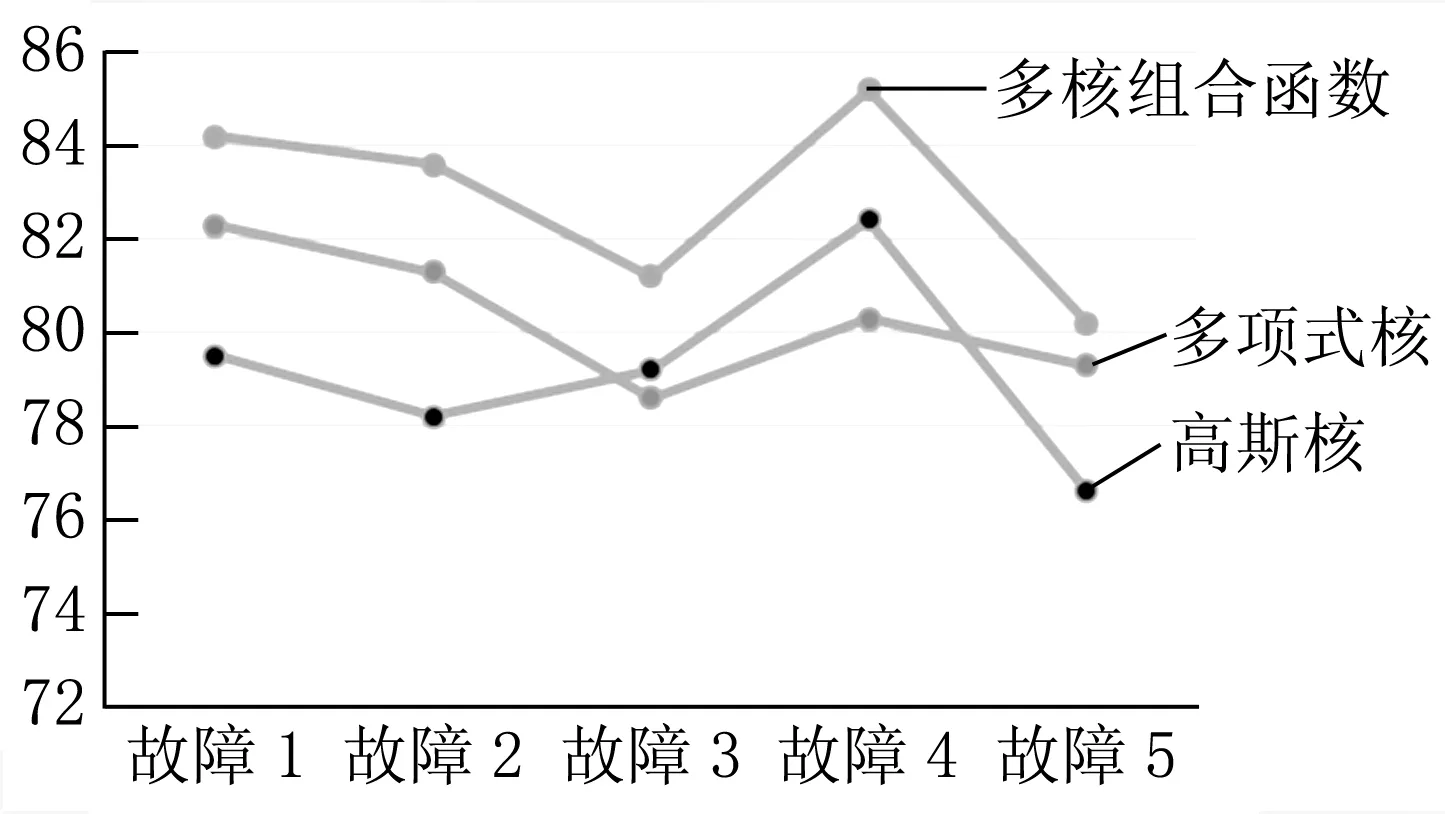
0 (8) 4.1.1 PCA算法 面对高维数据维度灾难问题,我们需要对数据样本进行降维,通过降维技术过滤数据样本中的冗余信息。PCA方法通过将原始数据通过线性变换映射到新的特征空间中,用尽可能少的特征组合表示原始数据。PCA算法首先对原始样本数据构成的n维矩阵去均值化,即求出每列的平均值,将该列所有数减去该平均值,使得每个特征的均值为零;接着求其协方差矩阵,根据协方差矩阵求出特征值及特征向量,将特征值从大到小进行排序,选择其中最大的k个,然后将对应的k个特征向量分别作为列向量组成特征向量矩阵;最后将样本点投影到选取的特征向量中。以上实现了将一组n维数据降为k维,其目标实现了将原始数据变换到k个正交基,使得各字段间的协方差为0,而字段的方差则尽可能大。 4.1.2 KPCA算法 KPCA是基于PCA算法的基础上引入核函数后的一种非线性分析方法,首先把核函数隐式地将输入空间转换到一个非线性特征空间中,接着在该非线性特征空间中进行PCA线性变换。对非线性特种空间中的样本数据集进行线性分析时,通过核函数进行隐式定义,无需进行直接计算,只需通过计算核函数的内积即可。针对离散数据集的对象,只能通过KPCA进行处理。例如:对于人脸图像,不同人之间的数据,存在着非线性关系,通过KPCA进行非线性分析,所得到的识别率远高于PCA算法。 尽管核函数在聚类分析中得到了有效且广泛的应用,但单个核函数均是基于单个特征空间,单核函数无法满足异构、不规则样本的分析。不同的核函数有着不同的特征属性,适用于不同的应用场合,通过组合多个核函数,对每个核函数赋予不同权重值,根据样本数据的特征属性区别映射到不同的特征空间中,构造组合成新的核函数,使数据样本在新的特征空间中得到更好的表现,能大大提高聚类分析的效果。但如何对单核函数进行组合,以及在组合过程中各核函数的权重是多大,是多核函数需要考虑的重点问题。根据核函数的性质,如果对多个单核函数加权后得到的核满足Mercer条件,则该核为核函数。 在构造组合核函数前,先了解核对齐。核对齐不仅可以衡量核函数参数选择的优劣,同样还可以表示核函数与目标函数或者核函数与另一个核函数之间的相似性度量,作为构造最优组合核函数的依据。设K1,K2分别为核函数k1,k2的核矩阵,则核函数对齐定义为: (9) 若理想核函数为yy′,则核函数k与理想核函数yy′的核对齐为: (10) (11) 应用内点法对以上半定规划模型求解权重βi,从而得出最优组合核函数。 4.3.1 降维多核聚类算法实现[3] 面对高维数据,采用传统的核函数进行聚类,效果不佳。首先,考虑先将高维数据采用PCA降维技术进行降维处理;再次,结合聚类算法的基本思路,将最优组合多核函数替代单核函数,对降维后的数据进行聚类分析处理。得到降维多核聚类算法描述如下: 输出:各类簇的样本; Step1:首先利用PCA降维技术实现对所输入的原始数据集D进行降维处理,得到降维后的数据集D′; Step2:将得到的数据集D′映射到构造的多核函数核空间中,根据聚类算法,随机选择m个样本作为初始簇中心点; Step3:计算其余样本对象到簇中心的距离,并归类到最相似的簇中; Step4:计算簇的新均值,重新选择簇中心; Step5:计算目标函数; Step6:重复Step2至Step5,直到目标函数收敛或中心点不再变化,结束算法。 4.3.2 降维多核聚类算法实验[5] 为了验证算法的实验效果,将基于多核的降维算法应用于机器故障诊断中,图1给出故障识别的精确率对比情况,从图可以看出新的组合核函数性能要高于单核函数,能够获得更好的聚类效果。 图1 故障精确率对比图 不同的核函数有着各自不同的特性,聚类过程中会产生不同的分类效果,所以最优组合核函数中权重的选择至关重要。本文首先分析了聚类的几种主要算法以及相似性度量的几种常见方法,接着分析了高维数据的聚类分析方法以及对核函数进行了介绍,针对传统单核函数的弊端,提出基于多核函数的高维离散数据聚类算法研究。4 基于多核的降维聚类算法分析
4.1 KPCA算法
4.2 多核函数构造[3-4]

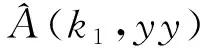

4.3 降维多核聚类算法实现
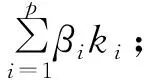
5 结语

