基于二次多项式拟合法的地形图高程精度提高技术

宋金元,岳春芳,王 健

(1.新疆农业大学，新疆 乌鲁木齐 830052； 2.新疆兵团勘测规划设计院，新疆 乌鲁木齐 830000)

国标GB/T7930-2008明文指出，1∶1 000平地航测不做空中三角测量，平高控制采用全野外布点。但是近些年的空三加密软件兴起，大比例尺图进行空三加密精度能达到要求，所以近几年新版规范才放开要求[1-2]。目前外业仍需像控点的布控才能满足1∶1 000地形图高程精度[3]。可见高程精度仍是研究难题，尽管差分GPS技术成熟，但布点工作量仍不小[4]。传统上空中三角测量内业法是通过控制影响高程精度因素，然后采取特殊的布点方案[5]以及新设计的标志点达到规范要求[6]，但通常精度不达标，只有重新布设点，工作量大。针对上述问题，本文利用IFAUAV-3无人机系统航测3个区域，分析航高是否影响高程精度，采取3个不同布点方案，通过测区加密分析精度提高状况。提出二次多项式拟合法[7]，利用其算出已知高程点改正值，精度得到提高且满足要求，通过3个测区高程点布设后的误差与二次多项式拟合后的误差对比可知，二次多项式拟合法不仅能提高精度，而且明显，优越于空中三角测量内业法。

1 试验区概况

1.1 测区概况

本文研究的测区位置在喀什范围内，测区分为A、B、C 3个区，分别为恰西勒克村、英叶尔村附近的岛屿、叶尔羌河特大桥附近河段，如图1所示。

图1 3个测区范围示意图

恰西勒克村位于莎车县荒漠镇管辖区内，紧邻三莎高速，测区西边多为沙漠，东边有稀少房屋及耕地。地势平坦且宽阔，地面高差小于10 m，测区面积为2 km2左右。

英叶尔村附近岛屿位于麦盖提县内，紧靠吾尔曼村、博孜村，位于310省道附近，麦盖提大桥下方，长1.5 km,宽500 m左右，岛上无建筑，地势较平，四周环叶尔羌河水。

叶尔羌河特大桥附近河段位于麦喀高速旁边，测区长度约1 km，宽1 km。河道平均宽度1 km，河岸无建筑区，多为荒地，摄影宽度1.5 km，测区相对平均高程12 m。

上述3个测区分别是极平坦区、小岛和河流，对于大比例尺航测而言，这3种地势具有代表性。分析航高是否影响高程精度，再结合不同的像控点分布，利用IFAUAV-3无人机实现1∶1 000航飞成图。

1.2 测区IFAUAV-3无人机航摄情况

3个测区位于新疆喀什地区，其采用普通的无人机航测不适合，风力作用对其影响较大，从而获取航测姿态数据精度较低[8]。本项目采用抗风能力较强的“IFAUAV-3”型号无人机航测。3个测区的航摄技术参数如表1所示， 测区覆盖采用不少于像幅的30%;每条航线拍照点按超出摄区所在相应测图比例尺图幅边界外各两条基线设计; 测区像片倾角采用不大于5°，最大不应大于12°[9]；航摄比例尺为1∶1 000。测区航带分布情况依次为测区A:6条航带76张影像；测区B:4条航带40张影像；测区C:4条航带32张影像。

表1 三个测区航摄技术参数

2 航高问题分析

试验之前，找出影响较大的因子，目前了解航高影响较大，却没有实例证实航高为关键因素；若证实航高影响较大，方法试验中采取同样航高避免带来影响，再实施空中三角测量内业方法。

结合上述分析，工程采用上述测区中的3个小测区A、B、C进行623 m,823 m,1 200 m不同高度航测，通过获取的数据中选出10个检查点的坐标值和量测高程，经计算可得各个区的平面误差和高程误差数据，再进行统计，如图2所示。从图2分析得知3个测区不同航高的高程误差起伏变化大，而平面误差起伏变化较小，从一定程度上可以看出航高对地形图的高程精度影响较大，说明存在航高的影响，需求出中误差，因此对3个测区做了精度对比和统计，如表2所示。

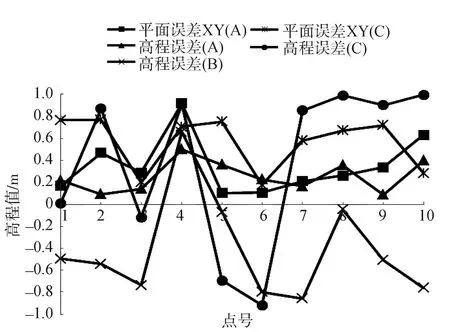
图2 3个测区地形图精度统计

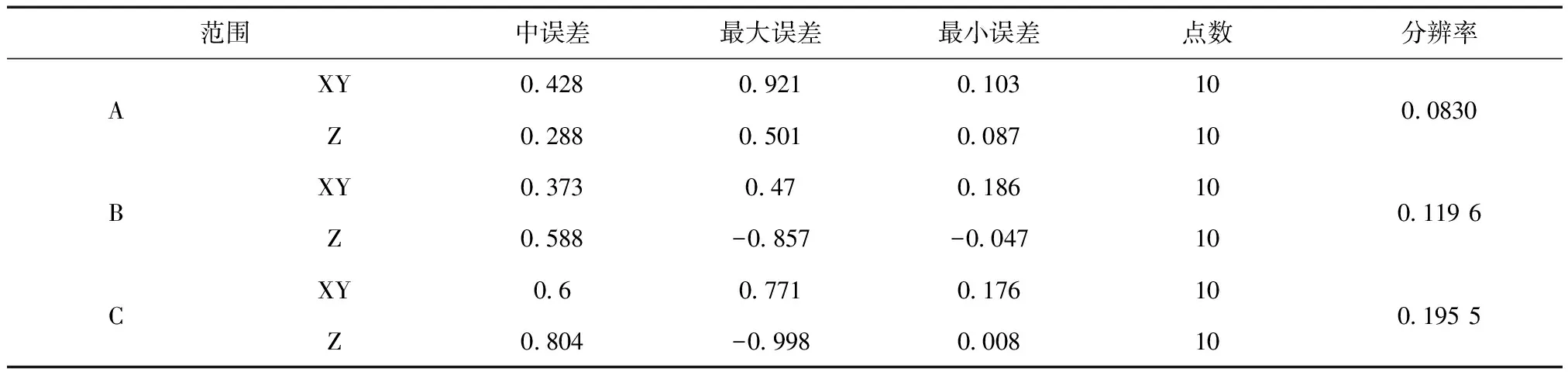
表2 3个测区地形图精度对比

在项目中应用各个测区分别测得的10个DOM平面检查点数据计算出平面中误差，依次分别为0.091 m,0.121 m,0.223 m。再结合表2绘制中误差直方图，如图3所示。根据CH/Z3003-2010规定[10]，在平原地带中DOM和地形图的平面精度要求1∶1 000为0.6 m，地形图高程精度为0.2 m。从图2和图3分析可得，3个测区的地形图和DOM平面精度都达到了1∶1 000地形图精度要求，但A测区高程精度却满足不了，因B与C区域高程中误差较大，精度也达不到规定。综上分析，航高的不同对地形图高程精度影响的确很大。

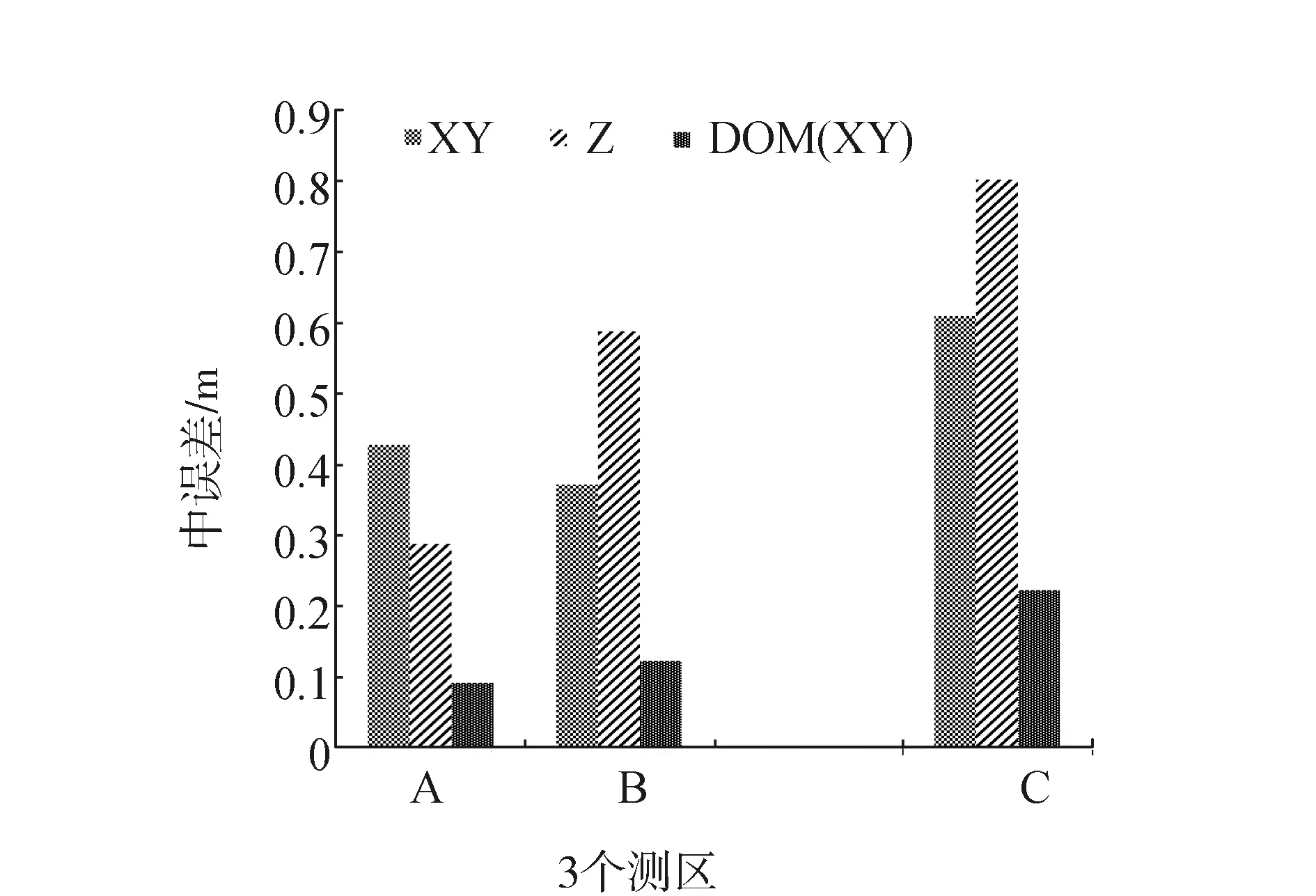
图3 3个测区地形图精度统计

3 方法试验研究

3.1 空中三角测量内业方法提高精度

3.1.1 空三加密点精度计算式

(1)

式(1)中的m1、m2、n、Δ和L分别指控制点中误差，公共点中误差，点的数量，残余控制点不符值和公共点较差,单位为m。

3.1.2 新像控点布设

为了避免航高关键因素对本方法的影响，故采取A、B、C航测高度一致。3个测区两种方式航测: A区先航测，再进行测量像控点;B区和C区采用先布设地标，再进行航测方式[11]。

1)A区采用区域网法布设且划分为2个区域，保证1条航线至少布1个点前提下，航向上，其间隔基线分别为2条和4条。此外，高程控制点在每条航线都布设点，在航向上，其基线数小于4条。如图4所示。像控点标志:在A区气候恶劣，地处沙漠边缘地带，利用半径为50 cm的细线做一个圆，利用白石灰洒在圆形上，白色石灰与黄沙相间，如图5所示。

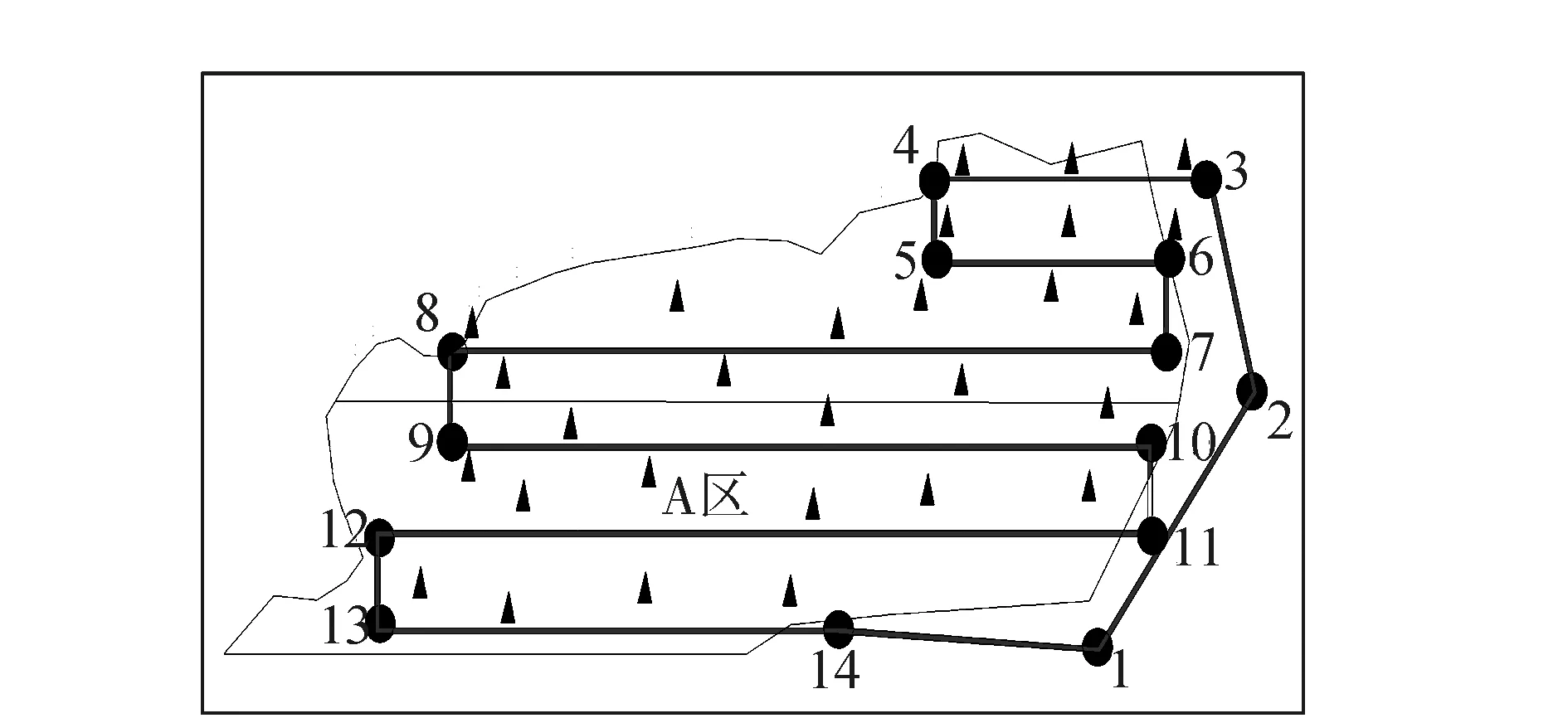
图4 A测区像控点的分布

图5 A测区像控点标志

2)B区采用航测之前区域网布设。岛上及其周围相距500 m布控一个像控点，同时航向每6条基线也布一个点。像控点在英叶尔村建筑区、田地和小岛选取的位置分别是选取平顶建筑正中，地物显眼地方，叶尔羌河岸边，然后在点上摆放像控点标志板，如图6所示。像控点标志:板面为40 cm×40 cm，板面颜色红白相间，中间小洞作用是对准点，如图7所示。

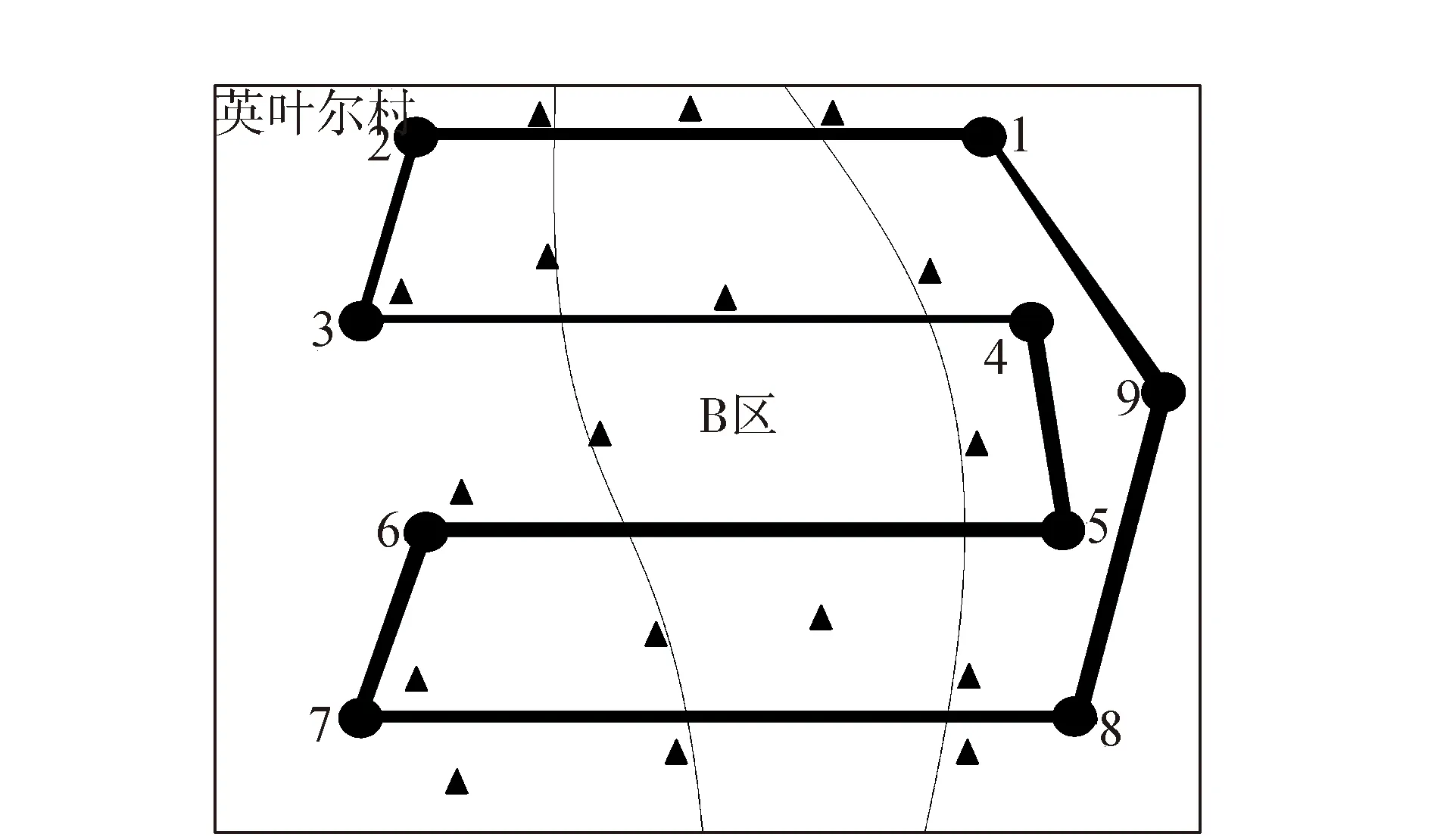
图6 B测区像控点的分布

图7 测区像控点的标记

3)C区像控点布设方法:沿叶尔羌河岸距离250 m进行布点，在航向上，隔6条基线布点且距离小于0.5 km。在飞机转弯处距离50 m布设双点和拐点处增添3个像控点进行测图，如图8所示。像控点标志:水泥地面上用黄漆画(1.2 m×0.4 m)“十”字线，并在中间用红色漆做半径5 cm的实心圆。用装满白色石灰的模板绘成“十”字(1.2 m×0.4 m)型在土地上，也用红色油漆在中心处做半径为5 cm的实心圆。

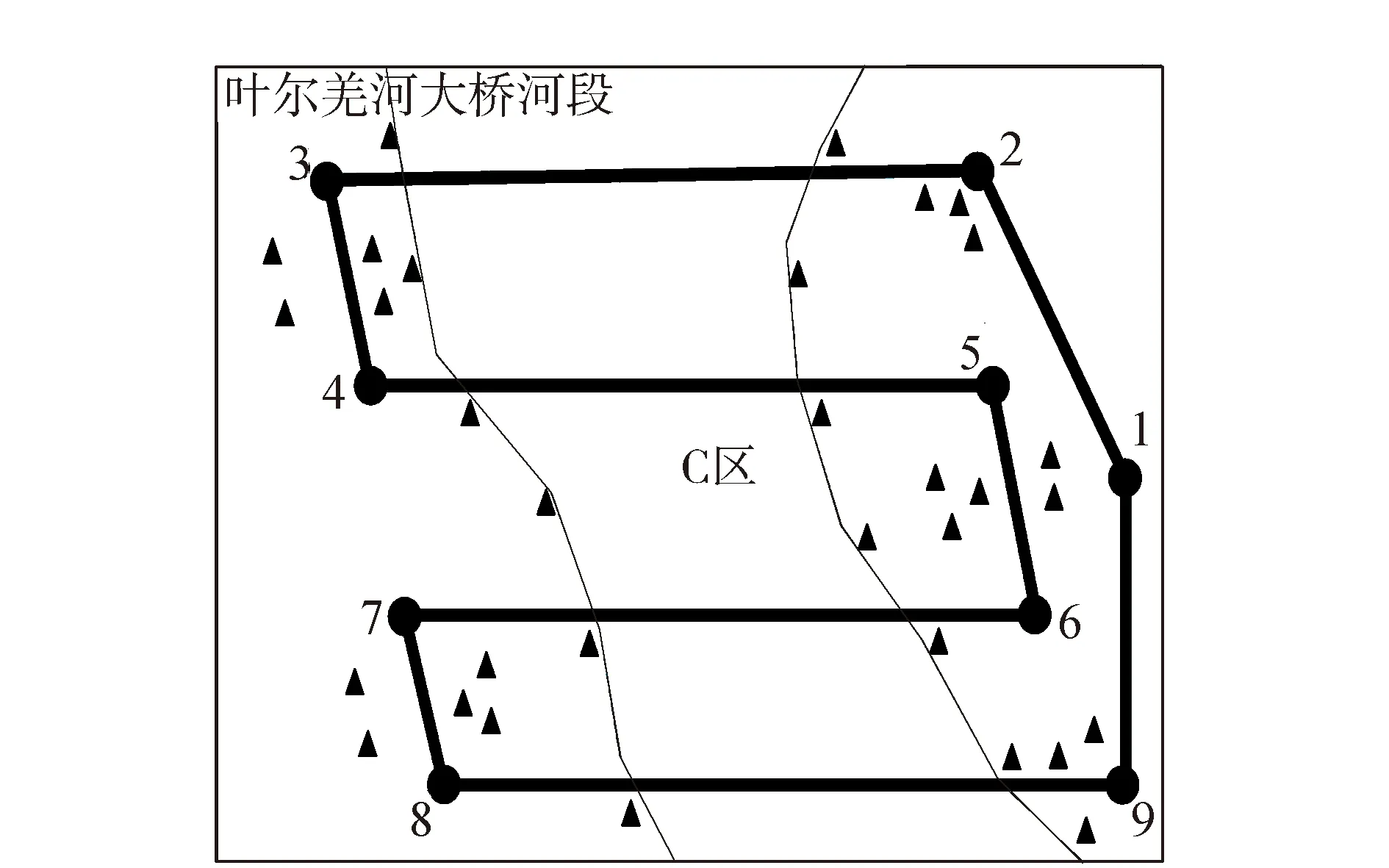
图8 C测区像控点的分布

3.1.3 像控点布设方法对高程精度的影响

将3个测区划分为2个加密区，见表3。据式(1)计算点中误差，点数小于20的用较差表示，见表4。A区由航测后布点、存在点分布不均匀、地处沙漠地带风沙大、石灰容易被盖住等影响。其次，野外布控像控点点位与加密时的地物点位不对应，导致加密的高程精度有误差。综合得到表4中A区所有点的精度平均值为：平面0.465 5 m，高程0.372 5 m；B区：0.452 5 m，0.372 25；C区：0.354 m，0.353 325 m，可知A区高程精度较低。B区是40 cm×40 cm标志版，即便受风沙影响大，高程精度却比较高；C区采用带状区域摄影方式和转弯处双像控点方式进行测图，同时像控点标志采用一种颜色喷涂且比B区大。通过区别A、B的布设特殊方法以及地标布设，C区的高程精度比A、B提高了大约0.02 m,但按照规范要求并没有达到精度要求。

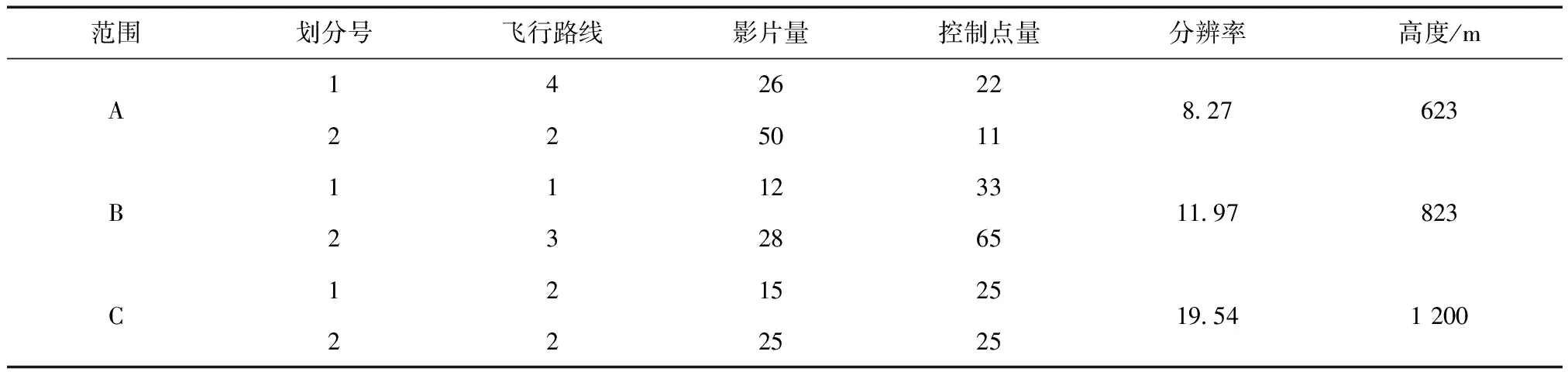
表3 测区加密分区

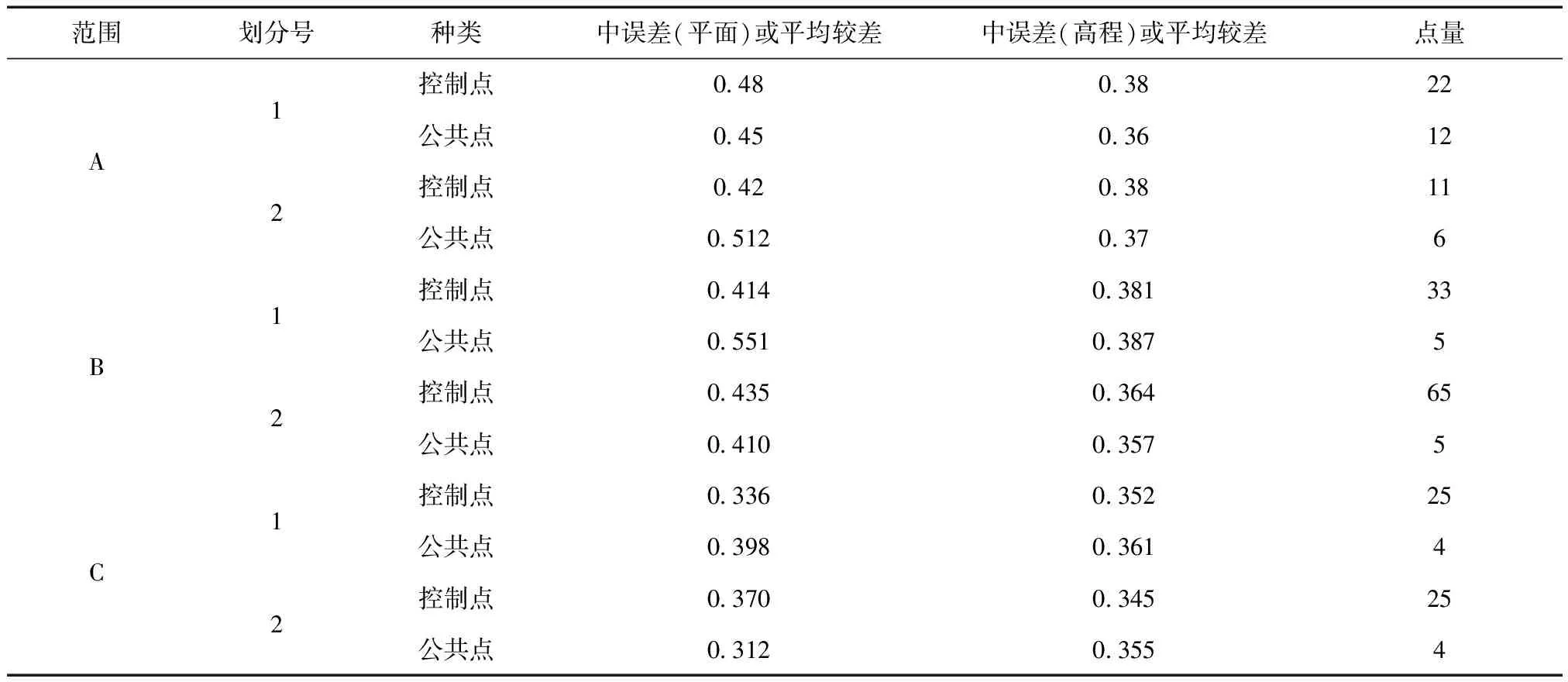
表4 加密精度统计 m

3.2 二次多项式拟合法提高精度

航高和像控点影响高程精度，通过上述试验，空中三角测量内业方法C区高程精度没有达到规范要求。本文为提高测区高程精度提出了一种二次多项式拟合方法，利用最小二乘拟合方法拟合实际测的高程检查点坐标值与量测的高程观测值之间的差值，即不符值。并且使拟合曲线上的改正值与实际的差值为最小[12]。14个高程点从C区中选取试验，H′是立体平台下量测高程检查点坐标，H是实测高程检查点坐标，则其差值为ΔH=H-H′，ΔH为高程坐标改正值，其构造的二次多项式为

ΔH=a1+a2·H′+a3·H′2.

(2)

需要从14个点中选取至少3个检查点才能求出式(2)中的系数。试验有多余观测值并列出二次多项式的误差方程式，如式(4)所示。利用间接平差方法算出改正参数，这时H′为观测值，则有:

ΔH=H-(H′+VH).

(3)

则误差方程式为:

lH=H-H′-VH=a1+a2·H′+a3·H′2-lH.

(4)

其中将14个高程检查点全部参与计算，则可以列取14个误差方程式，根据误差方程式写成矩阵形式:

V=AX-L.

(5)

其中：

(6)

V=[-VH1-VH2-VH3…-VH14]T.

(7)

(8)

(9)

将通过最小二乘原则[13]解算出的a1,a2,a3带入式(2)中，再根据立体量测的高程检查点坐标H′就可以得出该点的高程坐标改正值ΔH。将14个改正值加上原来观测高程得到的拟合后高程值，见图9所示。图9中的高程是减去1 200 m绘出的折线图。从图9中可以清晰看到改正前后误差对比，统计14个点误差值算出中误差为0.195 m，小于规定要求的0.35 m,因此二次多项式拟合法可以提高测区高程精度，达到规范要求。

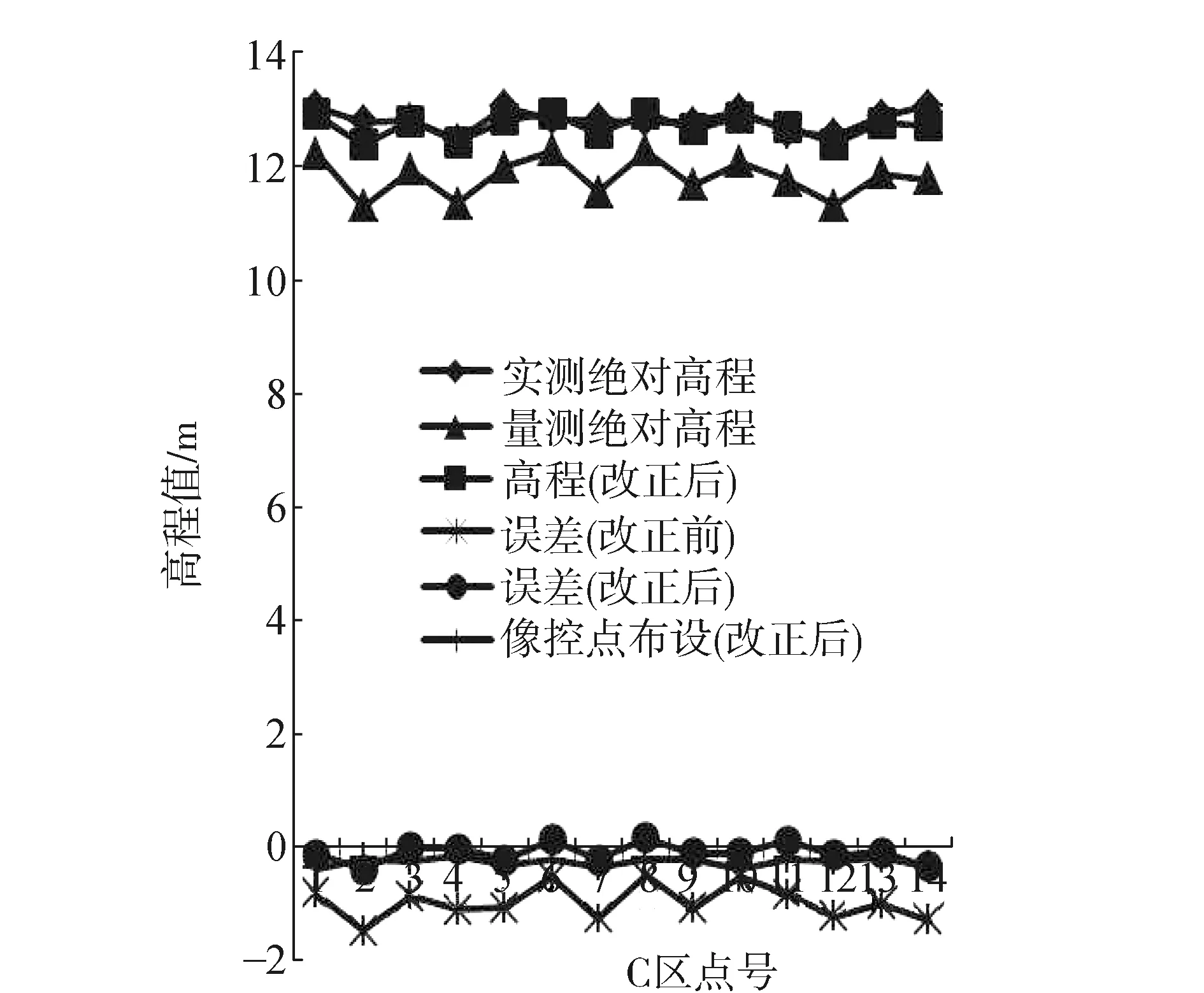
图9 C区高程拟合后与像控点布设改正后的对比

3.3 试验结果对比分析

根据规范要求，加密点的高程中误差精度为0.35 m，最大中误差限差为0.7 m,虽然C区的加密2区控制点精度为0.345 m，接近规范值，达到了规范要求。但C区中其他点都没达到要求，因此测区C即使有带状区域摄影、转弯处布设双像控点、点布设的密度大、用单一颜色油漆喷制图标等布设特点，高程精度仍不能满足。根据上述空中三角测量内业法的实施，再从 A、B测区中各抽取14个加密点，算出像控点布设后的误差值，即图9中的像控点布设(改正后)。将A、B测区14个像控点布设后的误差统计，结果如图10、图11所示。从图9，图10和图11比较可知，A区的像控点布设特点和B区的布设特点改变精度较小，像控点布设后的误差值均小于C区，很显然也小于二次多项式拟合后的误差值，C区和A、B比较改变得明显，其误差小于A和B且效果较好，但仍然小于二次多项式拟合法拟合后的精度。综合上述分析，二次多项式拟合法在地形图高程精度提高方面优越于空中三角测量内业法。

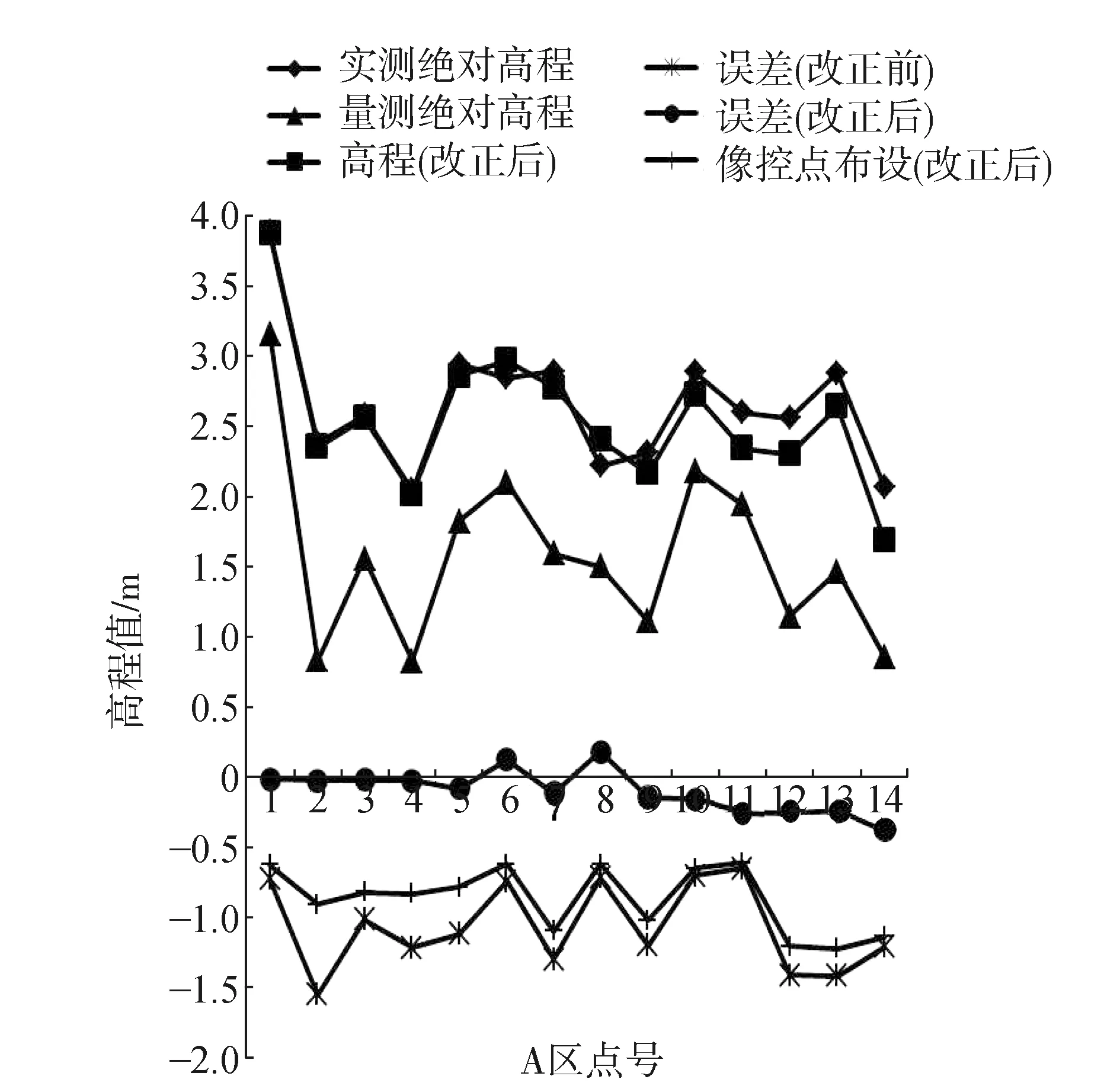
图10 A区高程拟合后与像控点布设改正后的对比

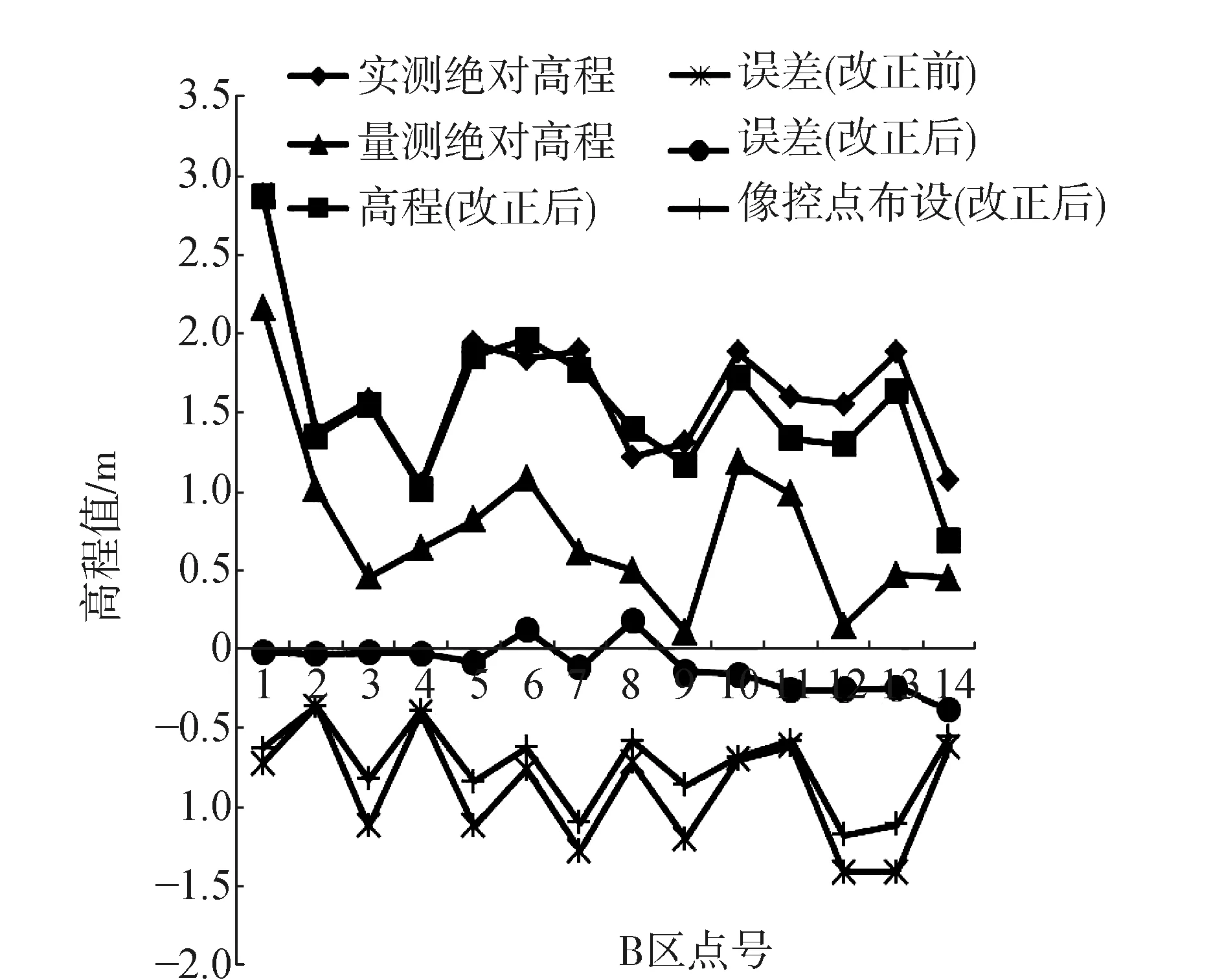
图11 B区高程拟合后与像控点布设改正后的对比

4 结束语

针对以往空中三角测量内业法提高精度不满足规范要求的问题，本文提出了根据二次多项式拟合提高高程精度的方法。首先对测区概况介绍，再分析影响地形图高程精度的航高因素，通过研究表明：新的像控点布设方案与新的地标布设措施可以提高地形图高程精度，但没有达到精度要求；利用二次多项式拟合方法可以提高其精度，而且效果明显。另外，本文只是对3个测区14个高程点进行拟合，当点数较多，拟合的效果还有待研究，二次多项式拟合法为以后研究地形图高程精度提供了依据。