基于抗差估计的Klobuchar-like电离层模型参数估计方法

刘 宸，赵 鹤，朱伟刚，刘长建，冯 绪

(1.北京卫星导航中心，北京 100094; 2.信息工程大学，河南 郑州 450001)

电离层延迟误差是卫星导航定位中重要的误差源之一，目前应用最为广泛的是Klobuchar电离层模型[1-2]。Klobuchar模型简单，电离层延迟修正率约50%～60%[3]。为了满足日益增长的导航定位精度的需求，不同的Klobuchar模型的精化方案被提出，均在不同程度上提升了模型的修正率，其中文献[4]在对各种适用范围较广的模型精化方案进行归纳总结的基础上，提出了适用于不同尺度区域的Klobuchar-like模型，具体模型如式(1)。

(1)

式中，A、B、C分别为夜间延迟关于时间的常数项、一阶项、二阶项系数，A2为白天余弦函数振幅，A3为电子总数目峰值的地方时时刻，A4为余弦函数周期,它们均为纬度φM的多项式，具体取值方法参照文献[4]。

当前，电离层模型参数估计方法有线性化后序贯平差[5]或最小二乘求解法[6-7]、Klobuchar-self求解法[8]、松弛搜索法[9]和经验模型外推求解法[10]等。Klobuchar模型及其精化模型均为以未知参数为分段条件的分段函数，且Klobuchar-like模型更为复杂，另外参与参数拟合的数据中可能存在粗差或者异常值，如GIMs数据[11]等。因此，本文提出了基于抗差估计的Klobuchar-like电离层模型参数估计方法，该方法适用于Klobuchar模型及其精化模型这类以求解参数为分段条件的分段函数。

1 模型参数的拟合方法

由于式(1)为分段非线性方程，不易直接求解，本文将分两步对参数进行求解：

1)利用各站点的VTEC迭代解算出单纬度模型参数X=[ABCA2A3A4]T；

2)用纬度φM的多项式表示所有站点的单纬度模型参数求解其他系数。该方法同样适用于Klobuchar模型及其精化模型。

在求解单纬度参数X=[ABCA2A3A4]T时，通过泰勒一阶展开将式(1)线性化，即

VTECi=

(2)

其中，i为迭代的次数，Δ为

(3)

(4)

(5)

(6)

具体实现迭代解算出单纬度参数X的算法步骤为

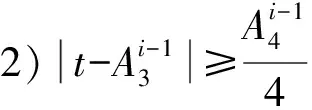
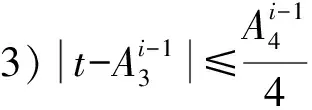
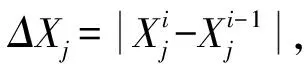
2 模型参数的拟合实验与分析

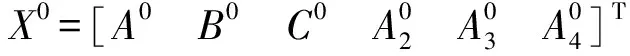
①爱丁堡蚀刻剂（Edinburgh Etch）由英国爱丁堡版画工作室画家佛兰德哈克·基克本（Friedhard Kiekeben）发明并命名。

初始权阵P分两种给定形式：一是将各站点每个时刻的VTEC值当作独立等权观测值，初始权阵P为单位权矩阵；二是将各站点每个时刻的VTEC值当作独立非等权观测值，可利用文献[11,15]给出的双线性内插法计算出站点每个时刻的VTEC值的RMS值，取pj=1/RMSj，若RMSj=0.0，令RMSj=0.1。初始权取pj=1/RMSj表示站点的VTEC值在精度上存在差异，更加符合实际情况。

本文分别以站点VTEC无异常值、单异常值以及双异常值等3种情况，分别利用最小二乘估计和抗差估计解算Klobuchar-like的模型参数。实验数据为利用GIMs获取的2016-09-22 CHAN站VTEC和RMS值。

2.1 无异常值时模型参数解算

图1给出了Klobuchar-like模型两种定权方法的最小二乘拟合结果。从图1中可以看出，初始权等权和不等权最小二乘估计曲线基本重合。

表1给出了初始权取不同权值时Klobuchar-like模型参数最小二乘解与VTEC修正率。分析表1可知，等权与不等权时模型参数间差异均在0.1以内，高阶项的参数解算结果的差异在0.001以内；等权最小二乘解的Klobuchar-like模型修正率为96.96%，不等权为97.05%，两者差异在0.1%以内。由此可见，等权和不等权结果差异很小，可以忽略不计。

当站点VTEC无异常值、初始权相等时，分别采用最小二乘和抗差估计解算Klobuchar-like模型参数，其中抗差估计的权函数分别取Huber、IGGⅢ和文献[16]提出的两种新的改进方案(分别记为IGGⅢ+和 IGGⅢ++，下同)，结果如图2所示。

由图2可知，最小二乘和抗差估计解算的VTEC曲线基本重合。为了清晰对比无粗差时抗差估计与最小二乘解的参数间的差异，表2进一步给出了抗差估计与最小二乘估计结果和修正率的差值。

表1 初始权不同权值时Klobuchar-like模型参数最小二乘解与VTEC修正率

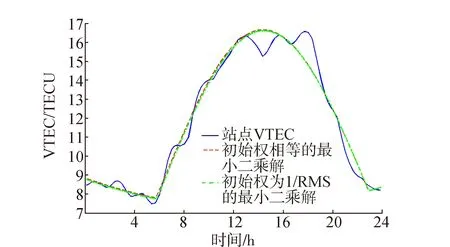
图1 Klobuchar-like模型最小二乘拟合结果

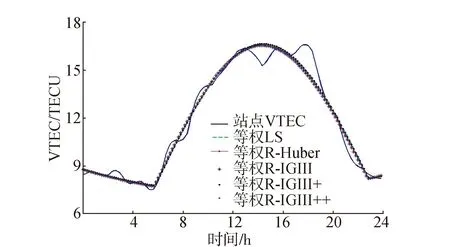
图2 初始权等权时不同权函数的抗差估计的参数拟合结果

表2 初始权等权时不同权函数的抗差估计与最小二乘参数解算结果的差值 m

分析表2可知，无粗差时，抗差估计解算的参数与最小二乘解算的参数间差异较小，基本在0.2以下，高阶项的参数(B和C)解算结果的差异均在0.01以内，模型修正率差异均在0.05%以内。由此可见，无粗差、初始权等权时，4种权函数的抗差估计结果与最小二乘解算的Klobuchar-like模型参数差异较小，模型修正率差异也很小，可以忽略不计。

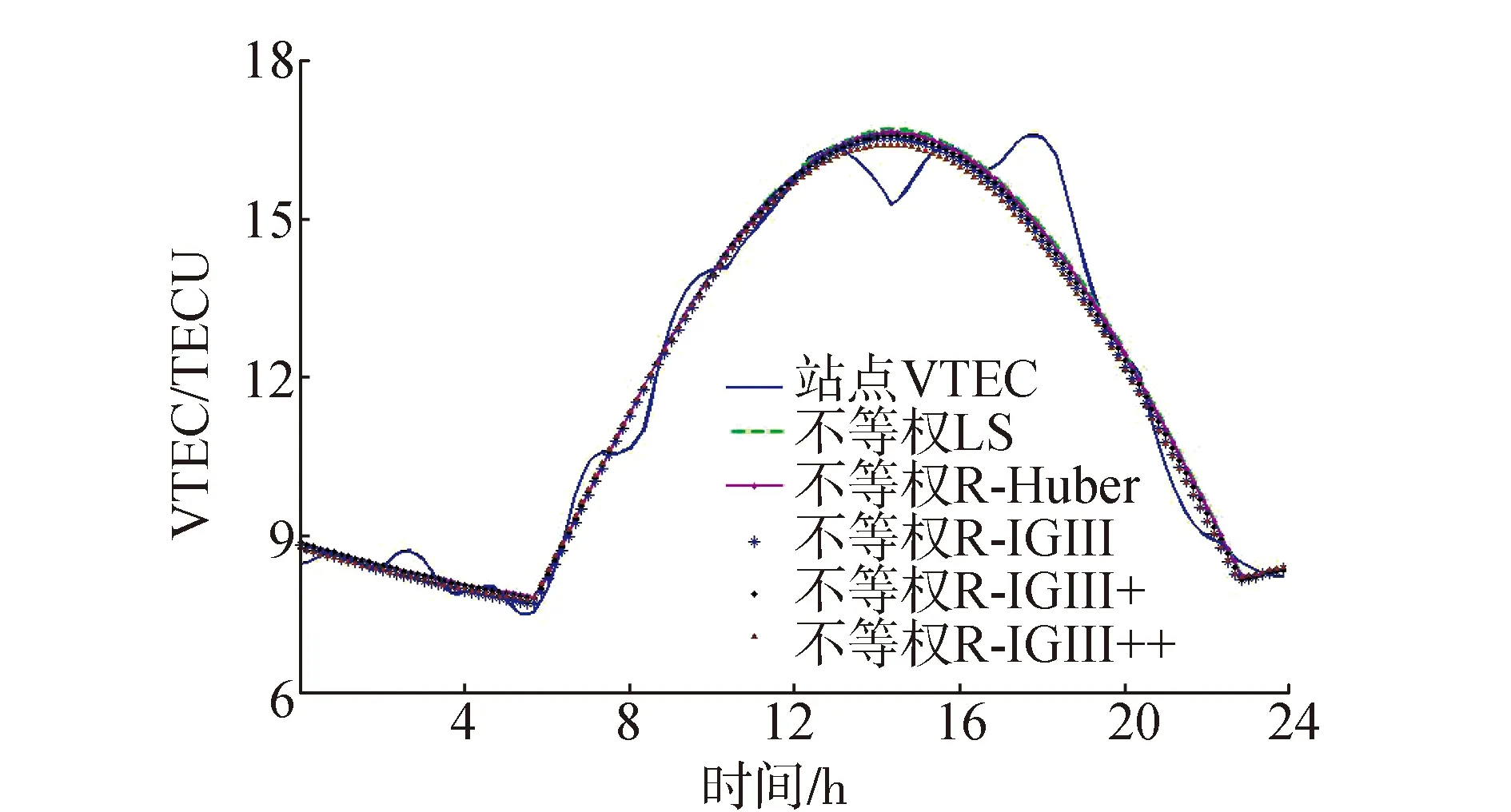
图3 初始权为1/RMS时不同权函数的抗差估计结果

表3 初始权为1/RMS时不同权函数时抗差估计方法参数解算结果与最小二乘解的差值

2.2 单异常值时模型参数解算

由图4可以看出2016-09-22 CHAN站的VTEC不含明显的异常值，为了满足单粗差的实验条件，在地方时3h处添加了一个“+40TECU”的粗差，进行模拟试验。图4给出了单粗差时初始权分别为等权和1/RMS的最小二乘估计的结果。从图4中可以看出，单粗差时，初始权等权和不等权最小二乘估计的参数所计算的Klobuchar-like模型的VTEC曲线夜间部分均偏离了站点VTEC，而白天的拟合效果较好。造成该现象的原因在于，粗差所加入的位置在夜间3 h处，而白天的VTEC并未加入粗差。同时可以看出，初始权为1/RMS的最小二乘估计参数计算的Klobuchar-like模型VTEC偏离稍远。

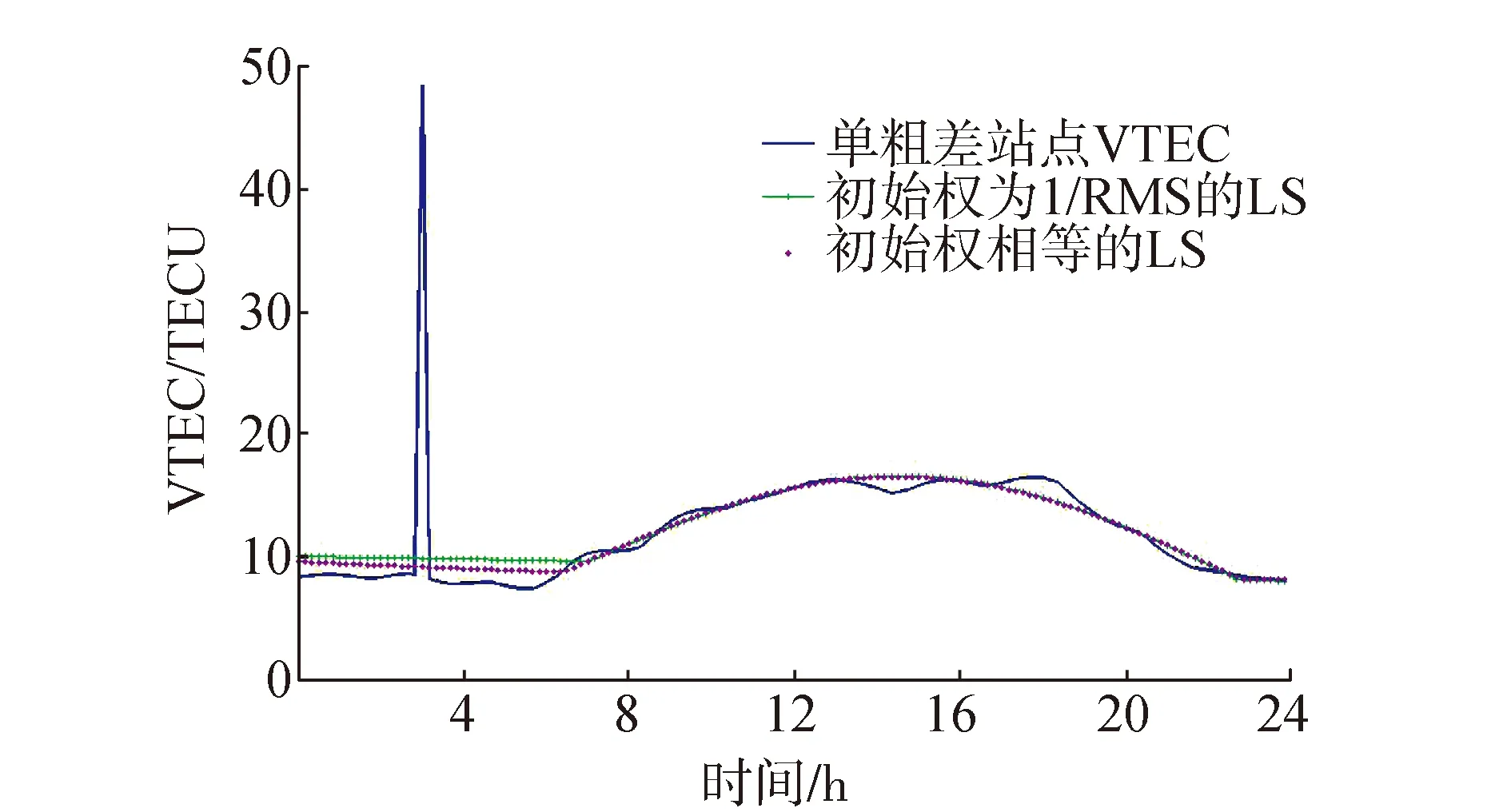
图4 单粗差时Klobuchar-like模型最小二乘拟合结果

图5给出了含单粗差、初始权等权时分别采用最小二乘和抗差估计结果。从图5中可以看出各种权函数下的抗差估计的结果非常符合无粗差时的站点VTEC变化趋势，表明了抗差估计的有效性。

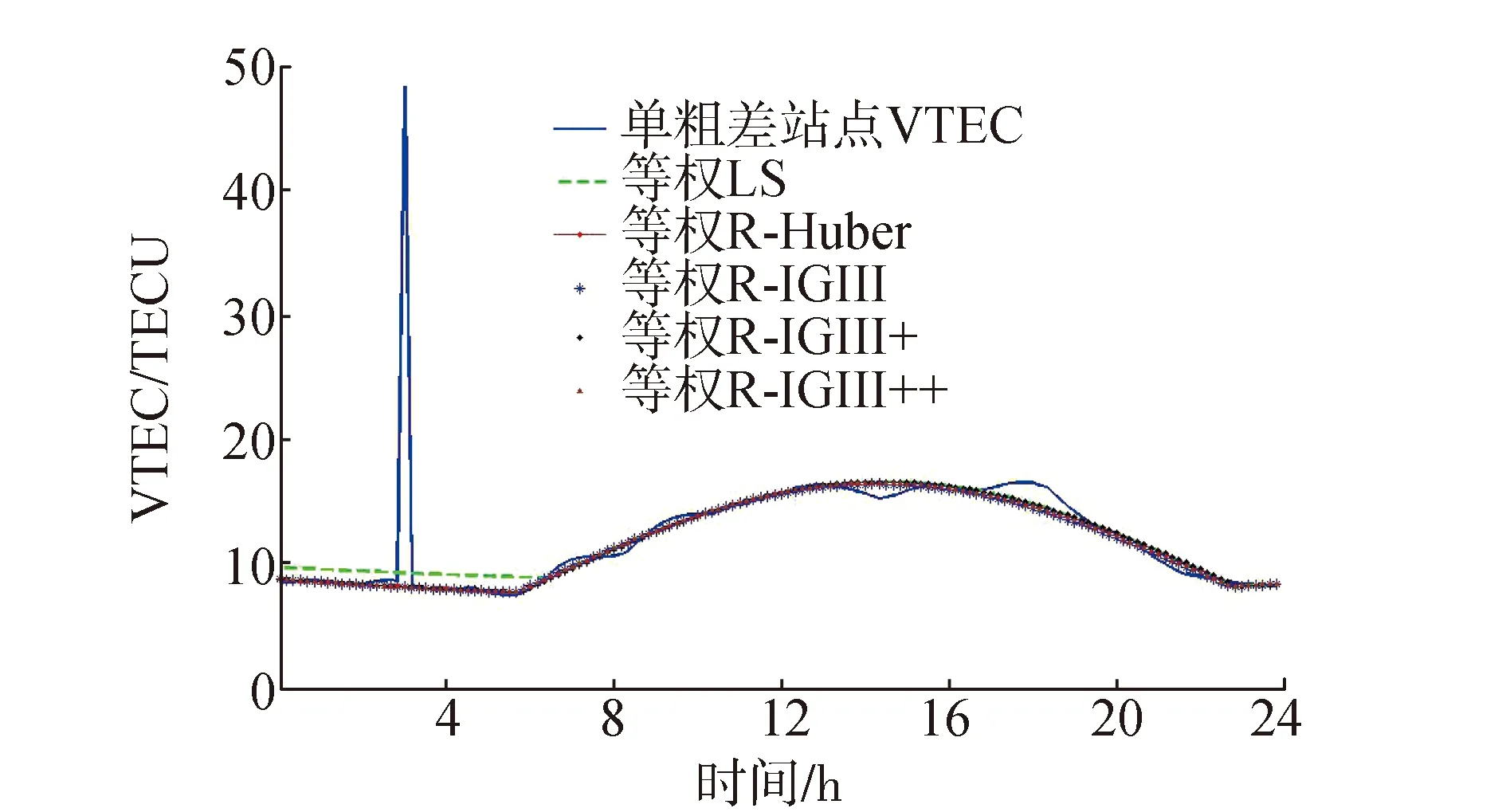
图5 单粗差、初始权等权时不同权函数的抗差估计结果

表4进一步给出了它们与无粗差、始权等权时最小二乘估计的模型参数解和修正率的差异。由表4可知单粗差时的最小二乘估计的模型参数与无粗差时的最小二乘估计参数差异较大，且修正率降低幅度也较大。此外由文献[11-12]可知，GIMs设定的异常值为999.9TECU，实际GIMs中还有更大的异常值(约3500TECU)，如此之大的异常值将导致最小二乘估计的模型修正率骤降。抗差估计的模型参数差异均在0.2以内，高阶项的模型系数差异均在0.01以内，模型修正率差异也很小，最高为0.06%，达到了很好的抗差效果。

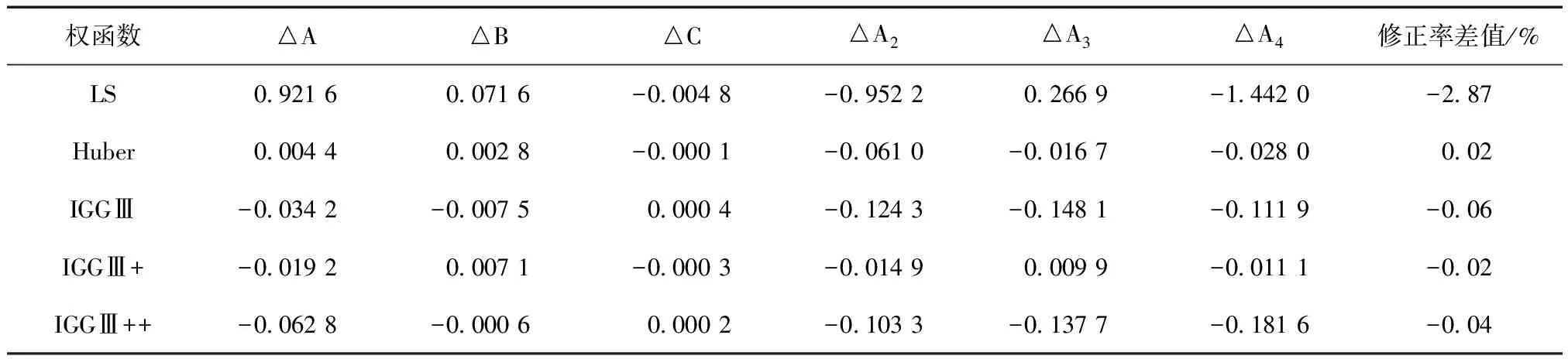
表4 单粗差、初始权为各种参数解与无粗差时最小二乘解的差值 m

当站点VTEC含单粗差、初始权取1/RMS时，分别采用最小二乘和抗差估计解算结果如图6。由图6同样可见，各种权函数下的抗差估计结果也非常符合无粗差时的站点VTEC变化趋势，同样表明了抗差估计结果的有效性。表5进一步给出了它们与无粗差、初始权为1/RMS时最小二乘估计的模型参数解和修正率的差异。由表5可知，单粗差时的最小二乘估计的模型参数与无粗差时的最小二乘估计参数差异较大，且修正率降低幅度较大；本实验所加入的粗差量级较小，修正率降低约5.10%，一旦粗差量级较大，最小二乘估计的修正率也将骤降。抗差估计的模型参数差异均在0.3以内，高阶项的模型系数差异均在0.02以内，模型修正率差异也很小，最高为0.04%，达到了很好的抗差效果。

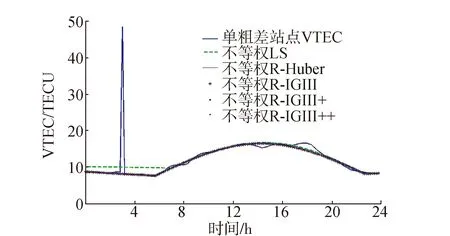
图6 单粗差、初始权为1/RMS时不同权函数的抗差估计结果

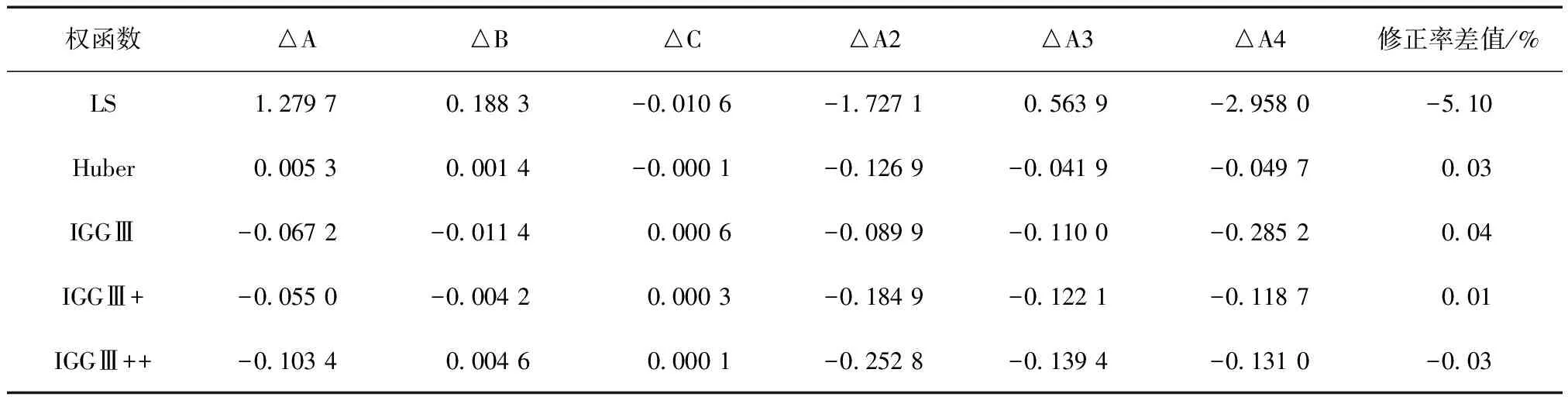
表5 单粗差、初始权为1/RMS时各种参数解与无粗差时最小二乘解的差值 m

2.3 双异常值时模型参数解算

为了满足双异常值的实验条件，在CHAN站的VTEC地方时4 h、和15 h处均添加了“+40TECU”的粗差，进行模拟试验。

图7给出了双粗差时初始权分别为等权和的最小二乘估计的结果。从图7中可以看出，双粗差时，初始权等权和不等权最小二乘估计的曲线白天和夜间部分均偏离了站点VTEC，且粗差位置附近偏离更为严重。

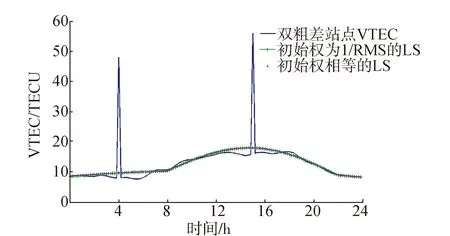
图7 双粗差时Klobuchar-like模型最小二乘拟合结果

图8给出了含双粗差、初始权等权时分别采用最小二乘和抗差估计结果。从图8中可以看出各种权函数下的抗差估计的结果非常符合无粗差时的站点VTEC变化趋势，表明了抗差估计的有效性。

表6进一步给出了它们与无粗差、初始权等权时最小二乘估计的模型参数解和修正率的差异。由表6可知单粗差时的最小二乘估计的模型参数与无粗差时的最小二乘估计参数差异较大，且修正率降低幅度也较大。实验所加入的粗差量级较小，则修正率降低约4.10%，一旦粗差量级较大，最小二乘估计的修正率也将骤降。抗差估计的模型参数差异均在0.4以内，高阶项的模型系数差异均在0.04以内，模型修正率差异也很小，最高为0.06%，达到了很好的抗差效果。

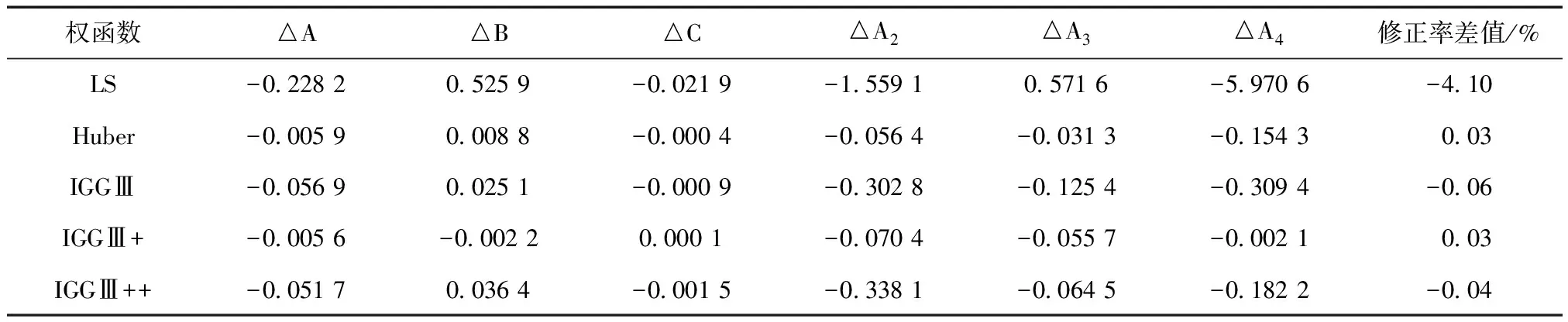
表6 双粗差、初始权等权时各种参数解与无粗差时最小二乘解的差值 m

当站点VTEC含双粗差、初始权取1/RMS时，分别采用最小二乘和抗差估计解算，结果如图9。由图9可见，各种权函数下的抗差估计结果也非常符合无粗差时的站点VTEC变化趋势，同样表明了抗差估计结果的有效性。表7进一步给出了它们与无粗差、初始权为1/RMS时最小二乘估计的模型参数解和修正率的差异。由表7可知，单粗差时的最小二乘估计的模型参数与无粗差时的最小二乘估计参数差异较大，且修正率降低幅度较大；本实验所加入的粗差量级较小，修正率降低约3.87%，一旦粗差量级较大，最小二乘估计的修正率也将骤降。抗差估计的模型参数差异均在0.5以内，高阶项的模型系数差异均在0.02以内，模型修正率差异也很小，最高为0.04%，达到了很好的抗差效果。

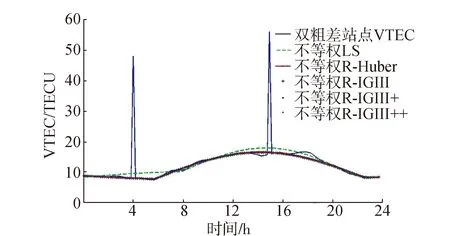
图9 单粗差、初始权为1/RMS时不同权函数时抗差估计结果

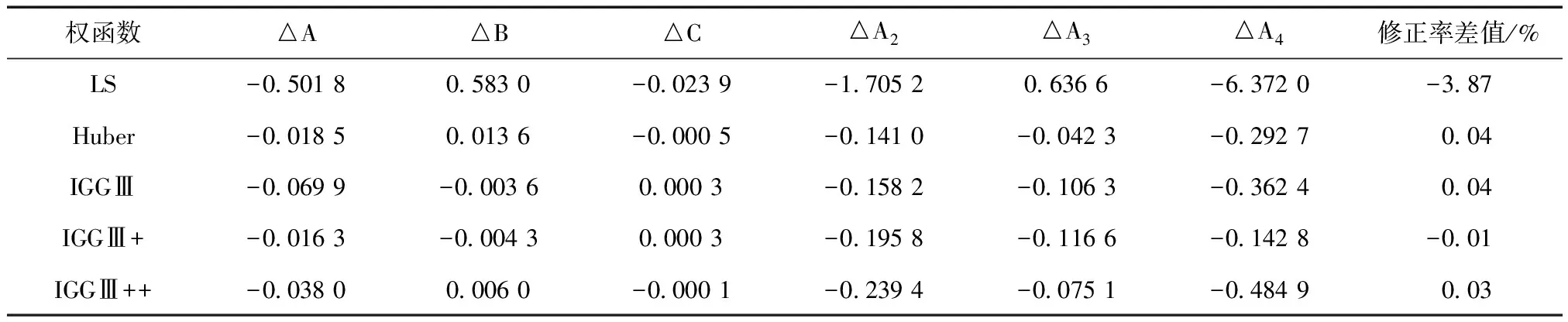
表7 双粗差、初始权为1/RMS时各种参数解与无粗差时最小二乘解的差值 m

由上述模型参数最小二乘拟合与抗差估计实验可知：当站点VTEC不含异常值时，最小二乘估计与抗差估计结果间差异很小，且模型修正率差异也很小，均可以忽略不计；当站点VTEC含异常值(包括单异常值和双异常值)时，最小二乘估计参数偏差均较大且模型修正率下降较大，而抗差估计解算结果与无粗差的最小二乘解和模型修正率差异均很小，可以忽略不计。因此，在不知道数据是否含异常值时，均可采用本文所提出的基于抗差估计的模型参数估计方法。

3 结 语

针对Klobuchar模型及其精化模型均为以未知参数为分段条件的分段函数、参数估计的数据可能还有粗差的情况，提出了基于抗差估计的Klobuchar-like模型参数拟合方法。该方法也可被借鉴与其他以未知参数为分段条件的分段函数的拟合情况。通过模拟实验验证了该方法的可行性与有效性。建议不论参数估计的数据中是否含有粗差，均建议采用基于抗差估计的参数估计方法。