一个非线性随机偏微分方程解的存在惟一性
王 昭, 鲍金洲, 李永坤
(长春工业大学 数学与统计学院, 吉林 长春 130012)
0 引 言
1951年,Ito的经典文章为随机方程引入了经典工具随机积分,随机方程自此进入了一个新的蓬勃发展的时代[1],类似于随机常微分方程(SODE)的多样性,随机偏微分方程(SPDE)同样广泛存在于各个领域中(例如物理、化学、生物等), 并且有可能会更好地解释世界,例如描述流体力学中的湍流、描述波在随机介质中的传播、描述化学中合金的分离以及来自生物学中的模型等[2]。
众所周知,高维非线性随机偏微分方程解的惟一性是重点和难点之一,随着非线性随机偏微分方程深入研究,对于二阶非线性方程的研究涌现了大量有意义的结果,Duan[3]利用转化思想处理了一类随机微分方程,将微观模型定义在带有小孔或不均匀的介质中,随着小孔的消失,微观模型自然转化为宏观模型;Zhang等[4]研究了随机非线性方程的光滑解的存在性;Zhang[5]、Breit[6]研究了非线性随机方程解的正则性。
随着高阶非线性抛物型随机偏微分方程研究重要性的显现,大量学者开始关注这个方向,Blomer[7]研究了四阶抛物型方程和表面增长模型;对于描述相变的随机Cahn-Hilliard方程, Da Prato等[8]利用经典的半群理论以及强Feller性质给出了方程弱解的存在惟一性,Cardon-Weber[9]给出修正温和解的存在惟一性,Wang[10-11]研究了带有不同随机项的解的相关性质,Duan[12]研究了S-H方程的随机形式,给出了解的存在惟一性等。
我们研究如下带有随机项的四阶抛物方程解的存在惟一性。
du+(uxxxx+uxx-u+u3)dt-dw=0
u(0,x)=u0(x), -l u(t,-l)=u(t,-l),t>0 (1) 首先,通过变量替换,随机微分方程可以转化为确定方程,并在适当的空间利用不动点定理,建立局部解的存在惟一性,再根据解对初值和随机项的连续依赖,给出整体解存在惟一性结果。 首先通过C(I)的闭包Lp(I),p=1,2,…,定义如下范数: 为了方便,令 H:=L2(I) 并考虑巴拿赫空间Lp(0,T;Lq(I))及其范数: 文中定义如下核心空间: E:L6(0,T:L4(I)) 由非线性项u3决定。 首先,给出如下结果。 引理1对于任何T>0,有 L(0,T;H)∩L2(0,T;V)⊂E (2) 且存在一个常数K,与T>0无关,则有 ‖u‖E≤K(‖u‖L(0,T;H)+‖u‖L2(0,T;V)) u∈E (3) 证明 利用Sobolev嵌入定理,则 且存在一个常数C1>0,则 (4) (5) 提高式(5)两边的阶数,并在[0,T]的区间积分,其中 下面的压缩映射定理是建立局部存在性的核心定理。 如果 F(0)=0 而且 对于 ‖z1‖E≤a ‖z2‖E≤a (6) 则方程 (7) 存在惟一的解z∈E,满足‖z‖E≤a。 引理3若A是一个在H上的负自伴算子 ⊂H⊂V′ 则A和S(t)=etA从V延拓到V′。 若 t∈[0,T],y0∈H,g∈L2(0,T;V′) 则 y∈L(0,T;H)∩L2(0,T;V) 对于L>0的某些常数,独立于T>0。 ‖y‖L(0,T;H)+‖y‖L2(0,T;V)≤L(‖y0‖H+‖g‖L2(0,T;V′)) (8) 推论1对于A,S(t)和y0为引理3中的定义,我们得到 (9) 证明 使用式(4)、式(5)、式(8)以及u:=S(t)y0有 则式(9)成立,对于 首先,建立局部解的存在惟一性,利用自伴算子A Au:=-uxxxx-uxx-(c+1)u (10) 注意A是一个严格的负自伴算子,可以通过负自伴算子定义(-A)a。定义域为 根据式(10),式(1)可以重写形式 du=(Au-u3+cu)dt+dw (11) 其中,Wiener过程中取值于可分的Hilbert空间H=L2(I)中,且其协方差算子为Q。 令 S(t):=etA,t≥0 利用随机积分定义wA(t) (12) 利用变换 y(t,x):=u(t,x)-wA(t,x),t∈[0,T],P.a.s (13) 式(1)退化成为确定性方程 yt=Ay-(y+wA)3+c(y+wA) (14) 满足 y(0,x)=u0(x) y(t,-l)=y(t,l)=0 (15) 满足式(14)的解,y可表示为积分形式 (16) y(t)=S(t)u0+F(y+wA)(t),t∈[0,T] (17) 下面给出式(17)y解的存在惟一性,也就给出了式(1)的温和解的存在惟一性。 在式(17)中,F:E→E是算子的连续延拓。 F0:C1([0,T];V)→E 定义为 (18) t∈[0,T] 其中 G0:C1([0,T];V)→E 定义如下 (G0u)(t)=-uux(t)+cu(t),t∈[0,T] (19) 鉴于式(17),并假设F是良定义的,关于应用引理2,我们给出了有局部解的存在性。 引理4G0定义如式(19),可以连续延拓到 G:E→L2(0,T;V′) 并且满足 证明 令u,v,ψ∈L2(0,T;V),<.,.>表示L2(0,T;V)和L2(0,T;V′)二者之间的对偶映射,我们得到 由此推出另一个重要的结论。 引理5 (20) 证明 在F0定义于式(18)和引理3,得到 F(u)(t)=y(t;G(u))∈L(0,T;H)∩L2(0,T;V) 此外,从引理1有 ‖F(u)-F(v)‖E≤K(‖y(.;G(u))-y(.;G(v))‖L(0,T;H)+ ‖y(.;G(u))-y(.;G(v))‖L2(0,T;V))≤ KL‖G(u)-G(v)‖L2(0,T;V')≤ 其中M2=M1KL。 定理1假设u0属于H,存在一个随机变量τP.a.s取值于(0,T],使得方程(1)在区间[0,τ]上存在惟一解。 证明 利用 z(t)=y(t)+wA(t)-S(t)u0 式(17)可改写为 (21) 对 F(z)=F(z+S(t)u0) 则式(17)与式(20)等价。 令 通过τ1得到 (22) K指在引理1、引理4和M的定义。 wA(t)是连续的且具有wA(0)=0。存在τ2使得 令 τ:=min{τ1,τ2} 并引入E E:=L6(0,τ;L4(I)) 其中Z1和Z2满足 ‖Zi‖E≤a,i=1,2 利用引理4和式(9),有 最后,应用引理2给出了z(t)的存在惟一性。 首先给出 推论2G的定义如引理4,则u,v∈E (23) 引理6式(17)的解y(t)连续依赖初值u0∈H和随机项wA(t)∈E。 由引理2得到y0和y1∈L2(0,T;V),因此(y0-y1)(t)∈V,对几乎所有的t∈(0,T)。使用S(t)的连续性和引理5,存在常数L1和C1使得 L1‖u0-u1‖H+ 利用Sobolev嵌入定理,存在y0和y1∈E,则存在常数C2和C3,使得 利用Gronwall不等式有 结论成立。 接下来,给出解的适当的估计。 引理7假设u0∈H,wA定义如式(12),并表示y的解 y(t)=S(t)u0+F(y+wA)(t) t∈[0,T] (24) 并且y满足 (25) 和 (26) 其中 以及 (27) 首先证明 (28) 乘以式(27),通过y(t)整合,得到 (29) 得到一个下界‖yxx‖H,利用 则有 (30) 接下来考虑式(29)的第一积分项,有 (31) 则得出结论 下面定理给出了方程整体解的存在惟一性。 定理2对于u0∈H=L2(I),方程(1)存在惟一解u(.,x)∈E,P.a.s.。 证明 对于区间[0;τ],从定理1我们有解存在为u(.,x)∈E,P.a.s.。利用式(13)和引理6,我们得出结论为u(t,x)在E上有界。P.a.s.对于所有的t≥0,这意味着解决方程(1)整体解的存在性。 利用不动点定理研究了一个随机偏微分方程,给出了解的存在惟一性结果,能够为解决模型所表示的实际问题提供一定的理论基础。1 预备知识

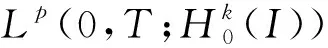
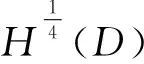
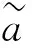
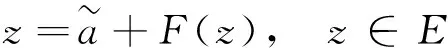
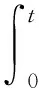

2 局部解的存在惟一性

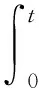


3 整体存在性
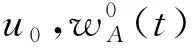
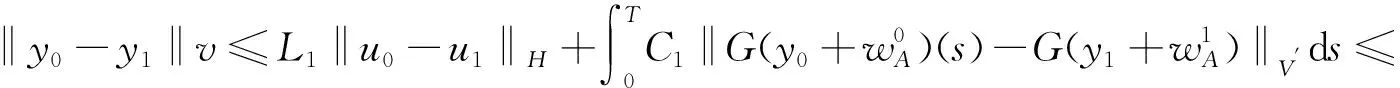
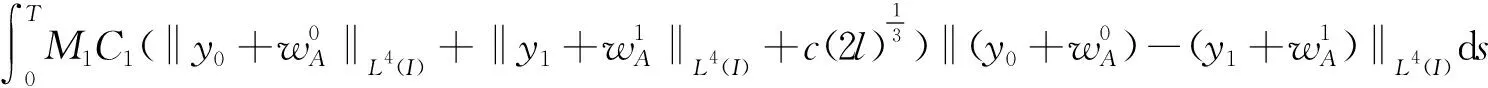
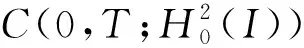
4 结 语

