多种坐标系下的圆环线圈磁场分布

温 欢， 孟雅俊

(1.中北大学信息商务学院 基础部, 山西 太原 030600;2.郑州工程技术学院, 河南 郑州 450044)

0 引 言

自从麦克斯韦将经典电学和磁学成功整合到一起，并且发展为麦克斯韦方程组，电磁学得到了更加深入的学习和应用。圆环线圈就是应用电磁学的一个非常典型并不可或缺的实例，它在电子、工程领域以及基础科学研究等方面都得到广泛的应用。目前，基于电子与工程领域，环形线圈开发出车辆检测器[1]、核磁共振等设备[2]；基于最近基础物理研究的热点，超冷原子量子模拟方面，环形线圈与激光配合构成磁光阱，由此可以将原子俘获并形成超冷原子量子气体[3-5]。

磁场的本质是电流的空间作用，圆环电流是最基本的理论磁体单元。在圆电流体系下，文中分别在球坐标系、柱坐标系、直角坐标系给出了明确的磁场表达式，因此，通过Mathematica软件可以得到整个空间准确的磁场值。结合并推广磁场表达式，可以获得任意位置、任意尺寸的通电螺线管的磁场梯度、磁场值等相关磁场指标。这些磁场表达式可以任意地套用到多种计算编程语言系统中。

文中进一步在亥姆霍兹线圈系统中，利用Mathematica软件在直角坐标系下计算了亥姆霍兹线圈三维、二维、对称轴向的磁场矢量图，然后分析得到两个载流线圈的总磁场在对称轴的中点附近的较大范围内是均匀的，该计算结果与实际非常吻合。

1 不同坐标系

建立直角坐标系，半径为a的圆环线圈放置在xoy平面内，线圈的中心与坐标原点重合，通过的电流大小为I，电流的正方向如图1所示(在此忽略线圈的横截面积)。

1.1 磁失势

根据磁场的“高斯定理”，通过闭合曲面S的磁通量恒等于0，表达式为：

·B=0

(1)

即磁通量的闭合曲面S是由边界线L所决定的。既然通过S的磁通量仅由它的边界线L所决定，就可能找到一个矢量A，它沿L做线积分等于S的磁通量[6]。对于磁感应强度B，这个矢量A叫做磁失势。

(2)

图1 圆环线圈在坐标系中的位置

图中测量点P在xoz平面内。

微分形式为：

B(x)=×A(x)

(3)

我们选择空间一点P(r,θ,φ)，因为环形线圈是对称的，将测量点选择在xoz平面内 (φ=0)。详细推导过程参见文献[7]。空间体系的磁失势就可以写为：

(4)

该关系式的积分可以用第一类完全椭圆积分K和第二类完全椭圆积分E来表示：

(5)

式中椭圆积分的参数k为：

(6)

在球坐标系下，磁场的不同分量为：

(7)

1.2 球坐标系

在球坐标系下(见图1)，对关系式进行求解可得到P(r,θ,φ)对应分量的磁场值和磁场梯度，如下：

(8)

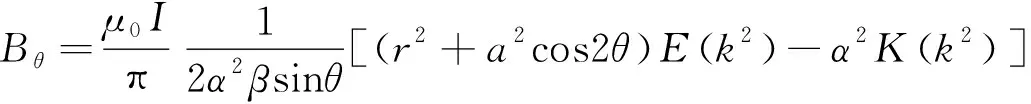
(9)

式中：μ0——真空磁导率。

α2=a2+r2-2arsinθ

β2=a2+r2+2arsinθ

因此关系式可以得到很好的简化。

通过Mathematica软件计算，可以得到磁场的空间微分形式：

(10)

[2α2(r2+a2)cosθ2]K(k2)}

(11)

[α2(-a4+a2r2-2r4+a2(a2-3r2)cos2θ)]K(k2)}

(12)

[3a6+2a4r2+a2r4+2r6+a2(5r2-a2)(r2+a2)cos2θ+(-7a5r+7a3r3-4ar5)sinθ+

a3r(a2-5r2)sin3θ]K(k2)}

(13)

1.3 直角坐标系

空间一点的坐标变化为直角坐标P(x,y,z)(见图1)。球坐标系和直角坐标系的变换公式为[8]:

即：

(14)

将上式代入球坐标系式(8)和式(9)，可以得到直角坐标系下对应分量的磁场值和磁场梯度，如下：

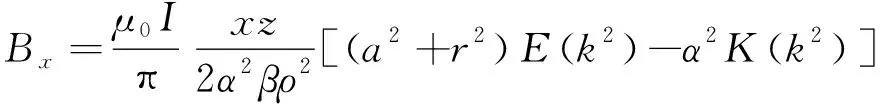
(15)

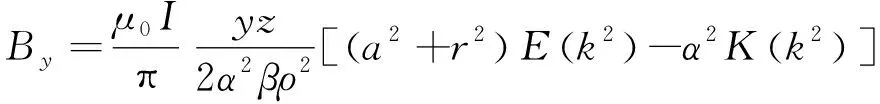
(16)

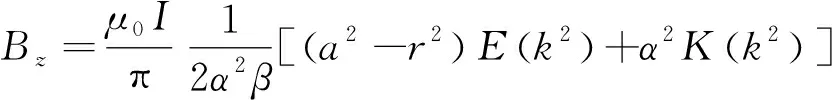
(17)

分析关系式(15)和式(16)可以看出，x、y轴磁场值有一个特点：

由此可知，磁场梯度满足：

关系式中：

ρ2=x2+y2

r2=x2+y2+z2

α2=a2+r2-2aρ

β2=a2+r2+2aρ

γ2=x2-y2

因此关系式可以得到很好的简化。

通过Mathematica软件计算，可以得到磁场的空间微分形式：

2ρ2z2(2x2+y2)+3z4γ)-r4(2x4+γ(y2+z2))]E(k2)+

[a2(γ(2z2+a2)-ρ2(3x2-2y2))+r2(2x4+γ(y2+z2))]α2K(k2)}

(18)

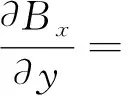
[r2(2r2+ρ2)-a2(5ρ2-4z2)+2a4]α2K(k2)}

(19)

[(ρ2-a2)2+z2(ρ2+a2)]α2K(k2)}

(20)

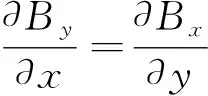
(21)

2ρ2z2(2y2+x2)-3z4γ)-r4(2y4-γ(x2+z2))]E(k2)+

[a2(-γ(2z2+a2)-ρ2(3y2-2x2))+r2(2y4-γ(x2+z2))]α2K(k2)}

(22)

(23)

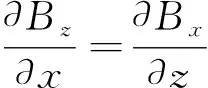
(24)

(25)

(26)

1.4 柱坐标系

空间一点的坐标变化为P(ρ,φ,z)，见图1。柱坐标系和直角坐标系的变换公式为[8]：

即：

(27)

将上式代入直角坐标系关系式(15)、式(16)和式(17)中，可以得到柱坐标系下对应分量的磁场值和磁场梯度，如下：

(28)

(29)

关系式中：

α2=a2+ρ2+z2-2aρ

β2=a2+ρ2+z2+2aρ

因此关系式可以得到很好的简化。

通过Mathematica软件计算，可以得到磁场的空间微分形式：

[a4-3a2ρ2+2ρ4+(2a2+3ρ2)z2+z4]α2K(k2)}

(30)

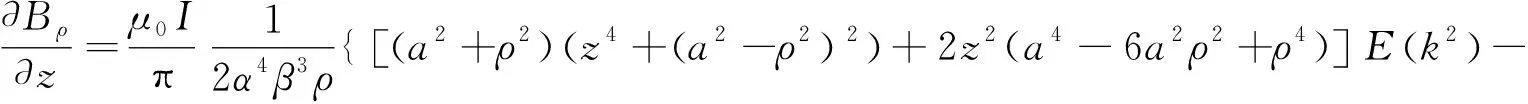
[(a2-ρ2)2+(a2+ρ2)z2]α2K(k2)}

(31)

(32)

(33)

2 亥姆霍兹线圈磁感应强度的数值计算

亥姆霍兹线圈是一对相同的载流圆线圈彼此平行且共轴，通以同方向电流，当线圈间距等于线圈半径时，两个载流线圈的总磁场在轴的中点附近较大范围内是均匀的[9]。故在生产和科研中有较大的实用价值，例如产生标准磁场、霍尔探头、地磁场的补偿、空间辐射磁场的测量和排除等。

亥姆霍兹线圈在直角坐标系中的位置如图2所示。

图2 亥姆霍兹线圈在直角坐标系中的位置

由图2可以看出，在直角坐标系下，亥姆霍兹线圈的对称中心与坐标原点重合，同轴线为z轴，线圈的芯径为1 mm，电流方向相同，大小为100 mA，内径r为60 mm，外径为80 mm，线圈高度为6匝，总匝数为10×6=60匝，两线圈间距d为30 mm。

磁力线矢量图如图3所示。

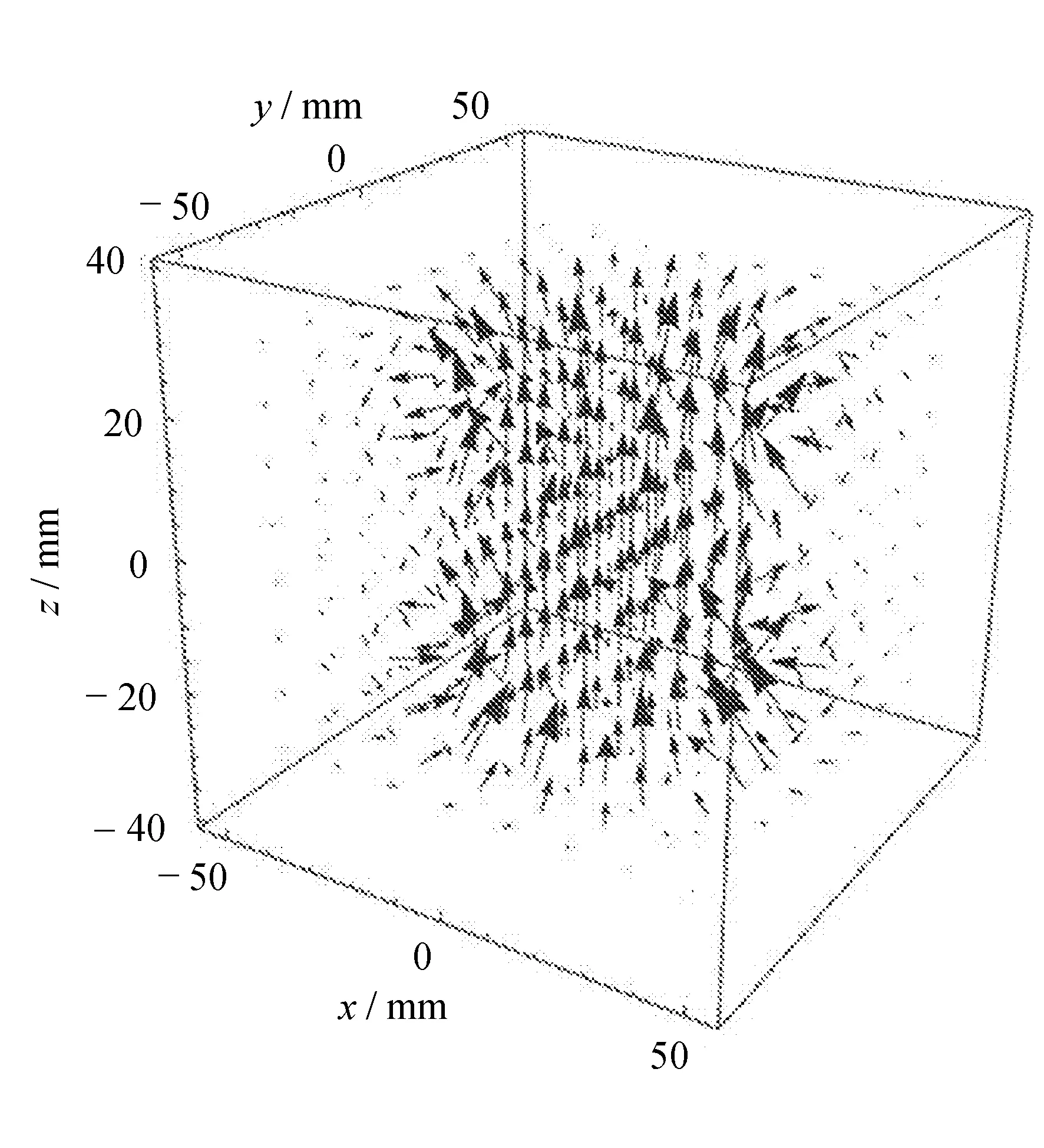
(a) 三维磁力线矢量图

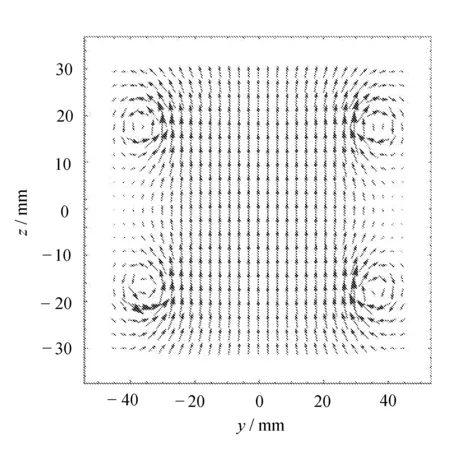
(b) 二维yoz平面(x=0)的磁力线矢量图

由式(15)～式(17)，利用Mathematica的函数ListVectorPlot3D[]可以得到{(x, -50, 50), (y, -50, 50), (z, -30, 30)}的三维磁力线矢量分布图，见图3(a)。

利用函数 ListVectorPlot[] 画出yoz平面(x=0)的磁力线矢量切片分布图，见图3(b)。

利用函数ListPlot[] 画出了三个位置处：(x=0,y=0)，(x=0,y=10)，(x=0,y=15)，沿z轴的磁场强度分布如图4所示。

图4 亥姆霍兹线圈的不同位置处，沿z轴磁场强度分布

不同间距的线圈组如图5所示。

图5 不同间距的线圈组

通过分析磁力线的疏密，如图3、图4和图5中间距d=30 mm的曲线，可知磁场在中心很大范围内为均匀磁场，尤其是沿着z轴，范围在{(x=0), (y=0),(z, -10, 10)} 的磁场为均匀磁场区，绘制的磁感线分布图符合“磁感线疏密程度反映磁场强弱”的物理要求，同时也满足亥姆霍兹线圈的特征。

不同间距的线圈组沿z轴(x=0,y=0)磁场强度分布。间距d=30 mm的亥姆霍兹线圈的磁场强度；间距d=24 mm的线圈磁场强度；间距d=36 mm的线圈磁场强度；距离xoy平面d=-15 mm的单线圈磁场强度；距离xoy平面d=15 mm的单线圈磁场强度。

3 结 语

推导、总结了圆环电流线圈在球坐标系、柱坐标系和直角坐标系的磁场值和磁场梯度表达式，为今后推导复杂的圆形磁场铺平了道路。这些磁场表达式简化了推导过程，可以推广到不同坐标系、任意位置、任意尺寸的通电螺线管系统中。

利用Mathematica强大的计算功能，画出磁力线的分布图，由此可以通过磁力线的疏密程度清楚地看出磁场强度的分布。最后在直角坐标系下计算了亥姆霍兹线圈三维、二维、对称轴向的磁场矢量图，通过分析两个载流线圈的总磁场在轴的中点附近的较大范围内是均匀的。