基于模拟退火粒子群的认知无线电功率分配算法

姜方达， 王宏志， 周明月

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

随着信息时代的发展，人们对无线业务的需求与频谱资源的低利用率之间的矛盾加剧。为了有效解决这一矛盾，提高频谱的利用率，认知无线电技术应运而生。认知无线电(Cognitive Radio, CR)作为一个智能无线通信系统，能够感知周围可利用频谱，在确保认知用户不影响主用户正常工作的前提下，与主用户实现共享传输。认知无线电网络通信的主要技术包括频谱感知，频谱分配合功率控制，针对不同技术已有很多算法被提出，如图着色法、进化算法、博弈论等。

近年来，越来越多的群智能仿生进化算法在认知无线电领域得到广泛应用，其中粒子群算法尤为突出。文献[1]用离散PSO优化无线电参数，粒子群平均适应度值下降，优化所得功率下降，收敛性差易陷入局部最优。文献[2]对离散PSO中的权重参数进行改进，仿真显示权重的设置对系统容量影响较大，并且随权重的增加，收敛性有所下降。文献[3-4]将PSO应用到认知OFDM网络中，前者系统容量略有下降，但仍在可接受范围内，同时收敛加快降低了计算复杂度，后者将遗传算法与PSO结合，虽然各方面均有所提升，但效果不明显，系统公平性不佳。文献[5-7]将量子计算与粒子群结合，虽然获得了量子计算的高精度，但却降低了收敛速度。文献[8-11]用二进制量子粒子群与二进制混沌粒子群优化系统公平性，两种改进均能获得较好的公平性，但增加了功率消耗。

上述算法针对不同目标进行优化，虽然得到了期望的结果，但都有不同程度的缺陷，主要是收敛能力和搜索能力差。针对这些缺陷，文中将模拟退火与粒子群结合采用动态惯性权重，提高了收敛能力和计算能力。在满足授权用户干扰阈值限制和认知用户SINR需求的前提下，实现认知用户传输速率最大化，获得认知用户系统最大容量。

1 系统模型

在认知无线电系统中，认知用户和授权用户分别拥有一对发射机和接收机。认知用户与授权用户实现频谱共享的前提是认知用户的接入不对授权用户正常工作产生干扰。在授权用户服务质量必须得到保证大前提下考虑其它约束才是具有实际意义的。对授权用户的干扰主要产生在每个认知用户发射机与授权用户接收机之间的链路上，考虑信道之间的增益，上述约束的数学表达式如下：

(1)

式中：Ith——PU的干扰功率阈值；

hi——SU-Tx和PU-Rx之间链路上的信道增益；

pi——认知用户i的发射功率。

认知用户伺机接入授权频带进行通信，通信质量也要得到保证，至少要满足自身需求的最低标准。认知用户的SINR表达式如下：

(2)

式中：hij——SU-Txj和SU-Rxi之间链路的信道增益；

pj——SU-Txj的发射功率；

Ip——授权用户对认知用户的干扰，由PU-Tx到SU-Txi链路产生，Ip=p0gi；

p0——PU-Tx的发射功率；

g0——PU-T和SU-Rxi之间的信道增益；

N0——信道上的背景噪声，假设噪声是独立随机变量CN(0，N0)。

上述约束的数学表达式如下：

γi≥γd

(3)

式中：γd——认知用户SINR的最低标准。

在满足式(1)和式(3)同时，期望认知用户系统容量最大化，在频谱共享的基础上实现数据的更快速传输，最大化认知用户系统容量的数学模型如下：

C2:γi≥γd

(4)

上述数学模型是一个非线性规划问题(Nonlinear programming， NP)，当用PSO解决NP问题时，一般根据约束条件采用外点法设置惩罚函数。惩罚函数如下：

(5)

式中:θ>0——惩罚因子;

gi(x)——由约束条件C1和C2设置的惩罚项。

则该系统模型下，粒子群算法的适应度函数为:

(6)

2 功率分配算法

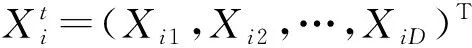
模拟退火算法是以物理中固体物质退火过程为出发点，将待解决的问题作为能量函数，从初始的高温活跃状态采用随机选择的方法降温至某一个稳定状态，其退火过程由加温、等温和冷却三部分组成。文中将等温阶段引入到粒子群个体和种群最优的判断过程中，采用Metropoils准则判断是否接受新的解，用迭代次数替换系统温度。变化后的Metropoils准则如下：

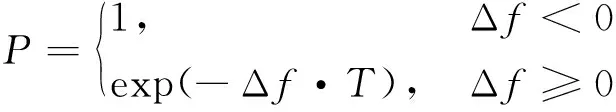
(7)

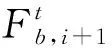
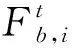
如果Δf<0，接受新解；否则以概率exp(-Δf·T)接受新解，T是当前迭代次数。通过上述操作建立了新的粒子群个体、群体最优更新规则，增强了粒子群挣脱局部最优的能力和收敛能力。由于等温阶段是一个动态的调整过程，我们考虑将粒子群速度更新中的权重参数也做出相应调整，改进后的速度、位置更新规则如下：

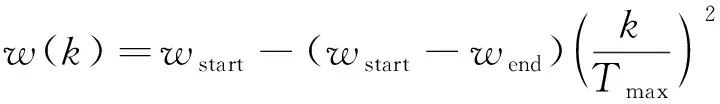
(8)

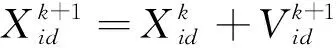
(9)

式中:w(k)——动态惯性权重相比于定值权重提高了计算精度;

wstart——初始权重;

wend——终止权重；

k——当前迭代次数；

Tmax——最大迭代次数；

c1,c2——正实数的学习因子；

r1,r2——分布于[0,1]区间的随机数。

为了避免粒子动态调节的步长过大导致粒子跳出搜索区域，建议将粒子的位置、速度限制在一个合理区间内[-Xmax,Xmax]、[-Vmax,Vmax]。

模拟退火粒子群算法流程如图1所示。

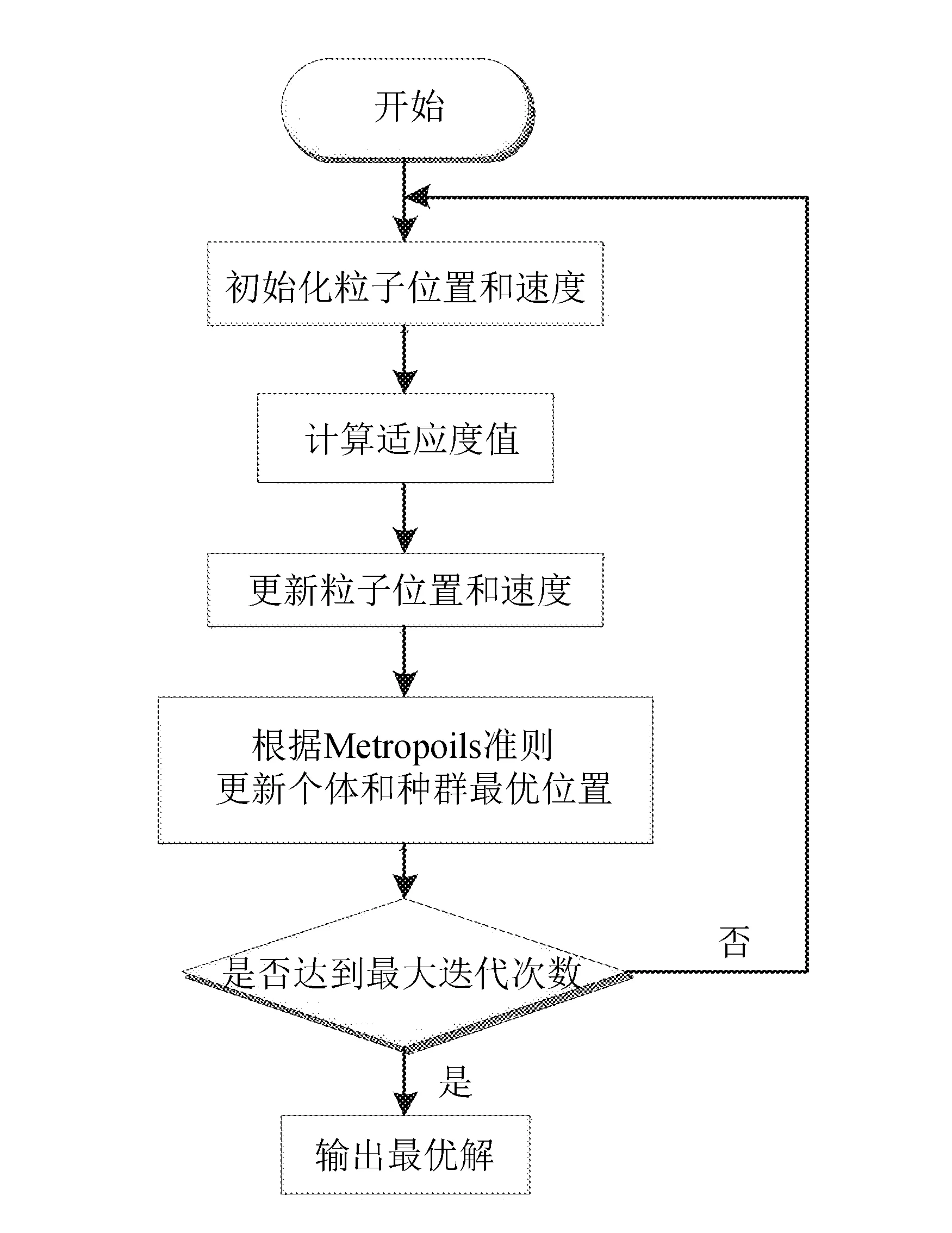
图1 模拟退火粒子群算法流程图

3 仿真分析

运用仿真软件Matlab R2014a进行仿真分析。对拉格朗日乘子法(Lagrangian Multiplier Algorithm， LAG)、PSO和模拟退火粒子群算法(Simulated Annealing Particle Swarm Optimization, SAPSO)进行了不同方面的比较。仿真参数设定见表1。

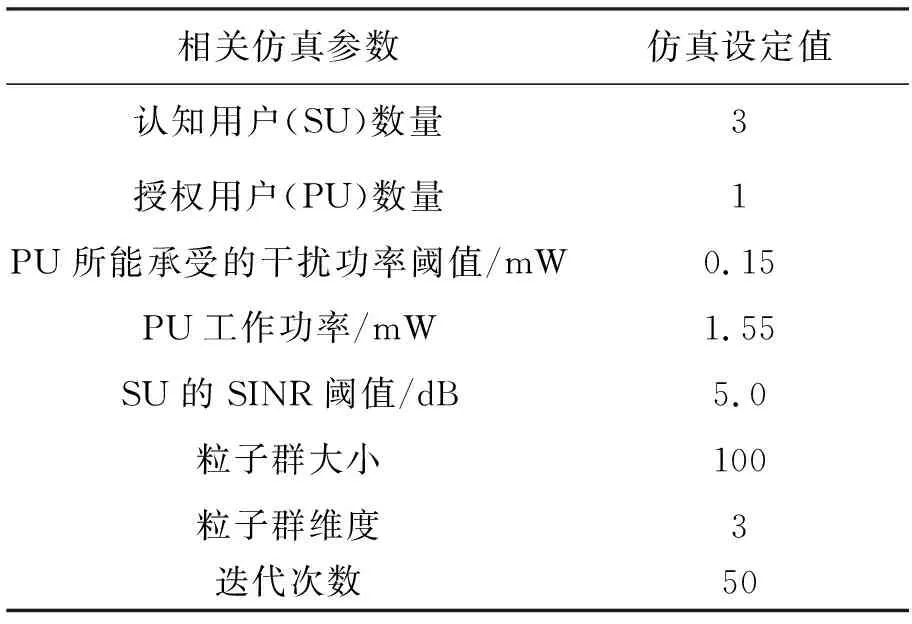
表1 具体参数设定方案

不同算法下认知用户发射功率与迭代次数的关系如图2所示。

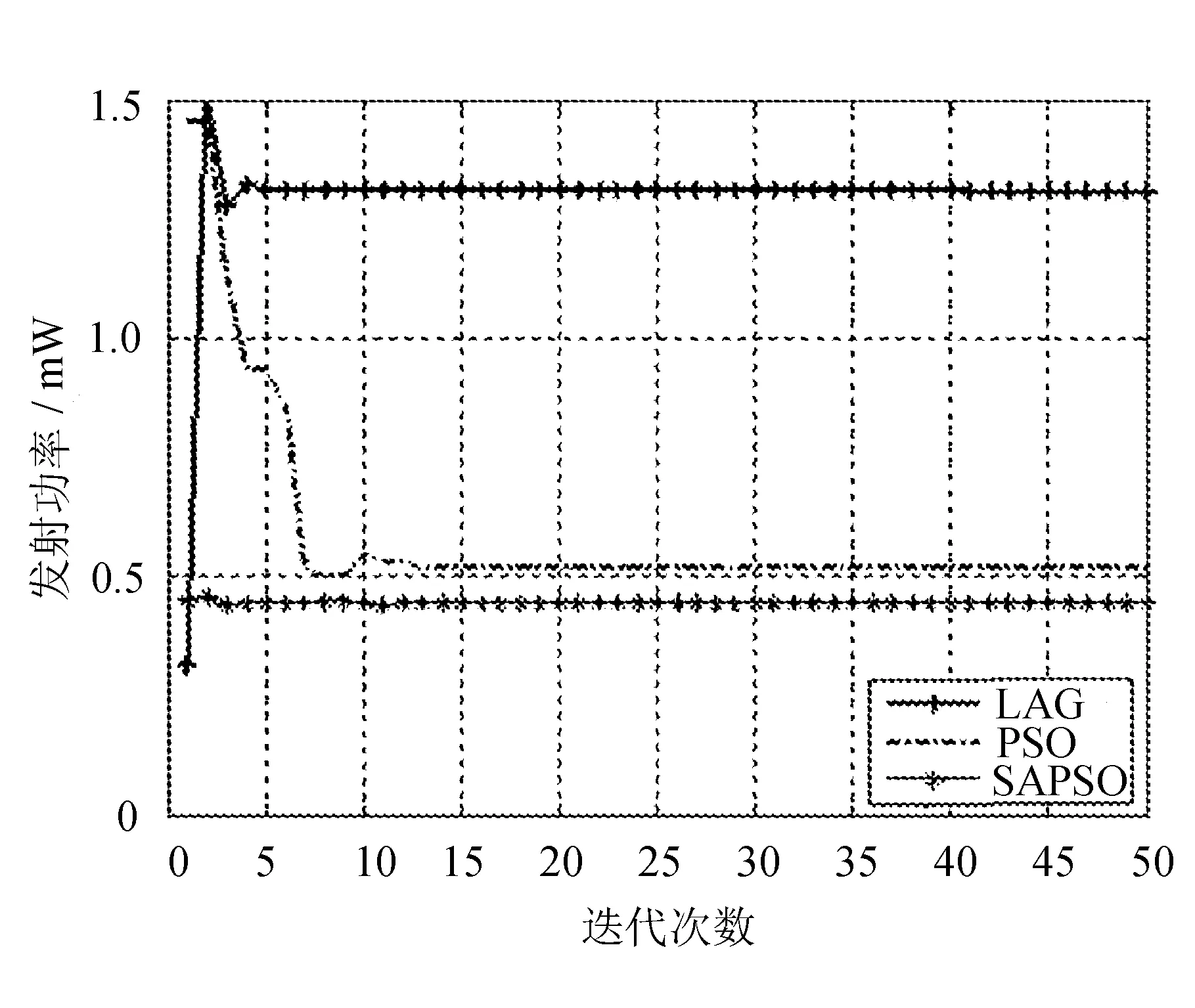
图2 不同算法下认知用户发射功率与迭代次数的关系

由图2可见，PSO比于LAG明显获得了更少的发射功率，有效降低了能量的损耗。SAPSO在PSO的基础上进一步略微降低了发射功率，并显著加快了收敛速度。

不同算法下干扰功率与迭代次数的关系如图3所示。

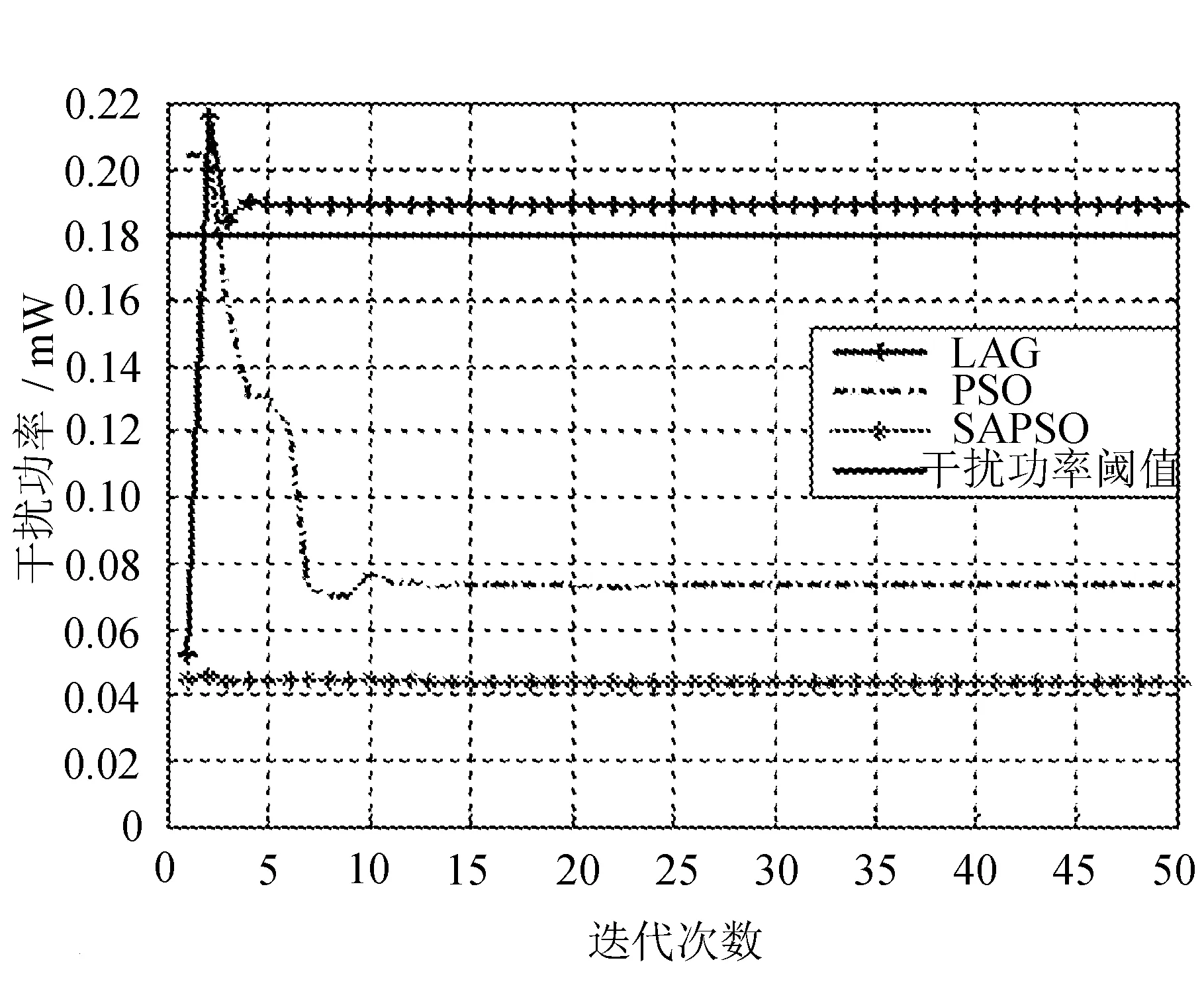
图3 不同算法下干扰功率与迭代次数的关系

在LAG中，认知用户对授权用户造成的干扰超过了干扰阈值，PSO和SAPSO的干扰功率明显低于干扰阈值。在发射功率降低的前提下大量减少认知用户对授权用户的干扰，不仅降低了能量损耗,还提升了SU的SINR。

不同算法下SU的SINR与迭代次数的关系如图4所示。

结合图3的干扰功率可见，SAPSO优化得到的SINR明显高于其他两种方法。当SINR阈值为5 dB时，LAG不能保证认知用户的正常通信，PSO与SAPSO不但保证了正常通信,并且SAPSO能达到更高的SINR。

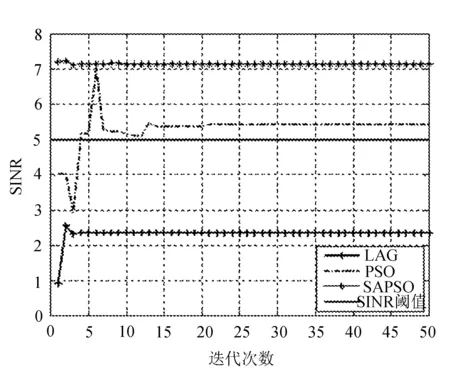
图4 不同算法下SINR与迭代次数的关系

不同算法下认知用户系统容量与迭代次数的关系如图5所示。

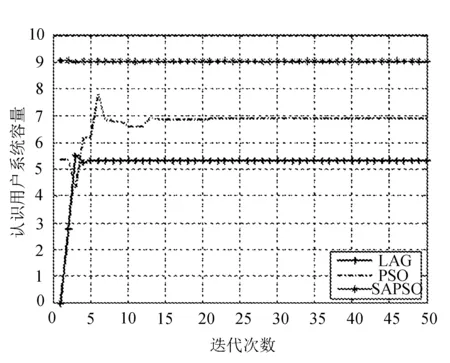
图5 不同算法下系统容量与迭代次数的关系

PSO与SAPSO相比于LAG获得了更高的系统容量。SAPSO在满足认知用户SINR的需求和授权用户干扰阈值前提下，尽可能高的提升认知用户的系统容量，实现系统容量最大化的目标。

4 结 语

将模拟退火算法与粒子群算法相结合，既保留了粒子群算法快速收敛的特性，也具备了模拟退火算法计算的高精度，同时增强了摆脱陷入局部最优的能力。实验结果表明，通过模拟退火粒子群算法优化，消耗的功率最小，对授权用户的干扰最低，信噪比与认知用户系统容量也是最大的。相对于粒子群算法和拉格朗日乘子法，改进后的粒子群算法是最优的。