基于NSGA2算法的ZPW2000A轨道电路维修策略优化研究

王瑞峰，陶荣杰

基于NSGA2算法的ZPW2000A轨道电路维修策略优化研究

王瑞峰，陶荣杰

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

针对ZPW2000A轨道电路传统维修的低可靠性和高维修费用问题，提出ZPW2000A维修策略多目标优化模型，对其维修策略进行优化。该模型采用求不交化最小路集方法求ZPW2000A的可靠度；考虑维修活动对系统可靠性和维修费用的影响，推导出ZPW2000A系统可靠度和维修费用表达式。将系统的可靠性和维修费用作为优化目标，采用非劣排序遗传算法(NSGA-II)进行优化计算，为决策者提供多种选择，并与传统方法进行对比，验证了该方法的有效性。

ZPW2000A；维修策略；不交化最小路集；NSGA-II；Pareto非劣解集

ZPW2000A轨道电路作为信号的重要基础设备，其可靠性对于行车安全极为重要。长期以来，轨道电路设备维修面对的是“期望设备高性能的运转与维护资源有限”的矛盾。而现阶段，我国铁路针对信号设备的计划维修主要以其服役时间作为根据，然而这会使部分设备组件没有将其功能充分发挥，造成维修资源的浪费，维修过量则影响设备的可靠性，造成安全隐患。因此，对ZPW2000A轨道电路维修策略进行优化研究，平衡维修资源和设备可靠性之间的矛盾，以最低的维修资源来达到对设备预期的性能要求，达到效益最优，非常具有现实意义。近年来，很多学者致力于轨道电路设备的维修策略和可靠性的研究。马涛[1]在使用故障模式和影响分析方法对设备故障进行分类的基础上结合RCM逻辑决断图对设备维修策略进行决策分析研究。米根锁等[2]在对轨道电路设备剩余寿命预测的基础上来调整维修方法。王文斌等[3]将故障模式影响分析方法和故障树分析方法相结合来研究ZPW2000A系统的可靠性。由此可以看出，对于ZPW2000A轨道电路设备维修策略和可靠性的研究大多停留在以可靠性作为单一优化目标或者研究对象，并没有考虑不同维修活动对设备的综合影响和平衡设备可靠性和经济性之间的关系。本文考虑不同维修活动对ZPW2000A可靠性和维修费用的影响，建立以ZPW2000A系统平均可靠性和维修费用为优化目标的维修策略优化模型。采用非劣排序遗传算法(NSGA-II)进行优化求解[4−8]，该算法通过模仿生物遗传进化过程中选择、杂交和变异来完成对问题最优解的搜索过程，得到一系列Pareto非劣解集，为决策者提供更多的最优选择。

1 ZPW2000A维修策略多目标优化模型建立

1.1 优化目标

ZPW2000A维修的核心问题是其可靠性，在此基础上追求经济性，从而达到效益最优。本文将ZPW2000A的可靠性和维修费用作为2个优化 目标。

在建立模型之前，首先对模型进行如下假设：

1) 设备的失效率服从威布尔分布；

2) 当设备运行到维修周期时，必须进行维修；

3) 当设备发生故障后进行维修，修复后的设备只能恢复到故障前一刻的状态，对设备可靠度不产生影响。

1.1.1 ZPW2000A可靠性

求ZPW2000A系统可靠性，应对其系统网络结构关系进行分析，采用邻接矩阵法求其最小路集[9]，再对最小路集进行不交化处理得到不交化最小路集，将每个设备的可靠度代入到系统不交化最小路集中，从而得到系统的可靠性表达式。

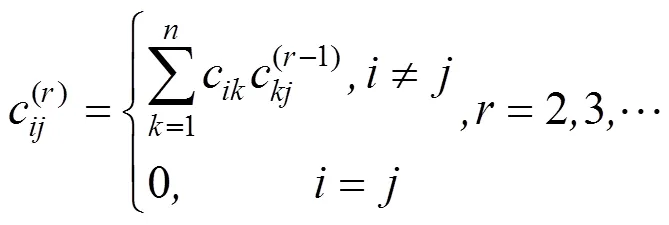
为了降低复杂系统的求解难度和计算量，通常要对最小路集进行不交化处理。若要求系统正常工作，则至少保证有一个最小路集正常。规定系统正常工作事件为：

其中：为最小路集个数。通过集合运算法则不交化得：

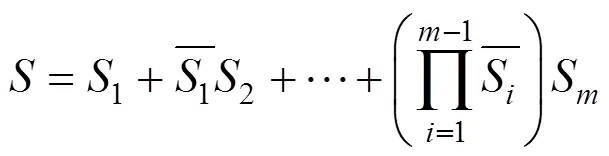
具体不交化方法为：

1) 将最小路集按照所含元素个数进行排序和编号；

2) 假定所有最小路集含个元素，有个最小路集，建立矩阵×，最小路集排序后，对每个元素位置进行标记，包含为1，不包含则为0；

3) 选出其中一个最小路集最为参照路集，把排在其前面的所有最小路集当作比较路集，删除比较路集和参照路集中一样的元素，并对每个比较路集剩余的元素取反。将取反后的元素相乘并简化，然后与参照路集相乘，所得为不交化后的结果，将所有不交化结果相加即为不交化最小路集。

通过上述方法可求ZPW2000A系统不交化最小路集。为了简化计算，忽略如钢轨等因素的影响，系统中发送器为+1冗余，取值为1，接收器为双机热备并联。ZPW2000A系统网络结构如图1 所示。

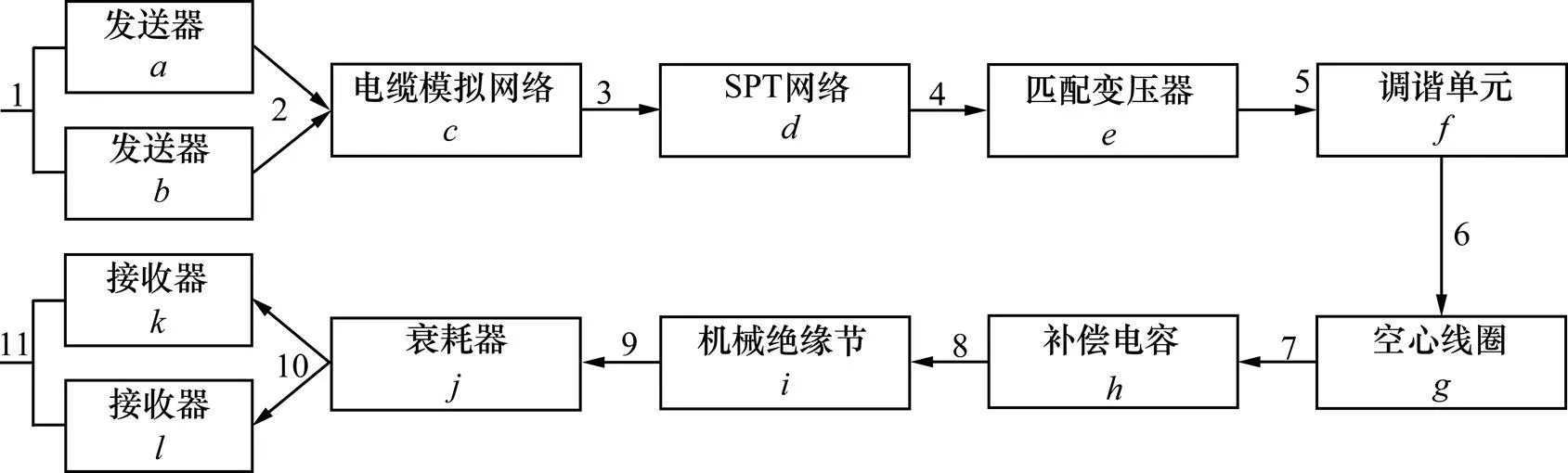
图1 ZPW2000A系统网络结构

由图1可得ZPW2000A系统的邻接矩阵：

对最小路集进行不交化处理，将得到的每个最小路集不交化结果相加，得到最终的ZPW2000A系统不交化最小路集为：

在ZPW2000A系统中，不同设备性能变化水平不同，因此，针对不同设备及设备所处不同质量状态选择合适的维修方式极为重要。目前，ZPW2000A的维修活动主要可分为修复性维修和定期预防性维修。修复性维修指设备故障发生后进行的维修活动，具有不可预见性。预防性维修是在便于调度管理和有准备的前提下进行的一种维修活动。而修复性维修和预防性维修都是通过具体的维修方式来实现的。本文主要考虑3种维修方式，如表1所示。

表1 维修方式

由于修复性维修只会恢复设备原有的功能，不会改变设备故障率，所以不考虑其对设备可靠性的影响。服从二参数的威布尔ZPW2000A设备组件可靠性分布函数为

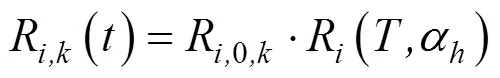
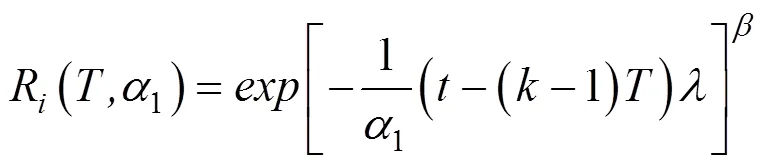
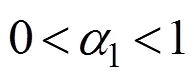
若采用1维修方式，对其性能的改善为

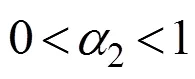
若采用3维修方式，对其性能的改善为：

式(12)表示设备变为全新。

将式(7)代入式(6)可得系统的可靠度为

由式(14)可对某维修策略下系统平均可靠性进行计算，将其作为维修策略优化目标之一。

1.1.2 系统维修费用

则在这段时间内，整个ZPW2000A系统修复性维修所需费用如式(16)所示

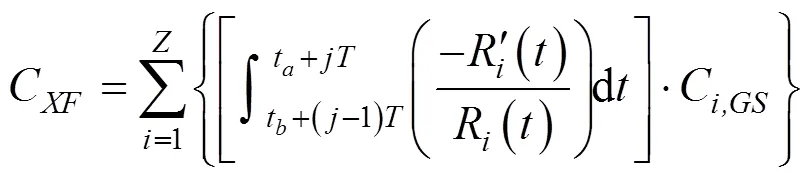
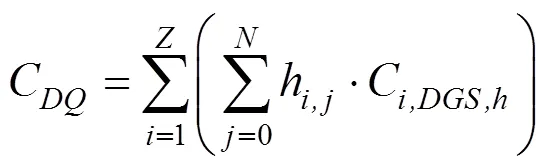
则ZPW2000A系统维修费用如式(18)所示。

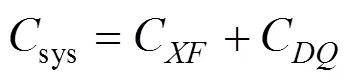
1.2 约束条件

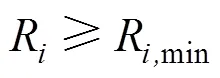
因此得到ZPW2000A系统维修策略多目标优化模型为：

优化目标如式(20)所示

约束条件如式(19)所示

2 NSGA-Ⅱ算法

NSGA-Ⅱ算法是Deb等学者于2000年在NSGA算法的基础之上提出来的，该算法能够得到一系列分布均匀、多样性较好的最优解集，适用于多个目标的优化问题，且相对成熟，广泛应用于桥梁、核电等领域的维修策略优化中[9−10]。

图2 NSGA-Ⅱ流程图

3 实例验证

3.1 编码和解码

采用二进制编码，该方法编码和解码操作简单容易实现。每两位代表一次维修活动信息，每次维修活动可以选择不维修、保养、局部更换和全部更换4种级别，对应的编码表示如表2所示。

若在优化年限内进行了N次预防性维修，那么一个设备维修信息编码长度为2N个，则系统的每一个维修计划长度为22N，即每个维修计划可用长度为22N的二进制数表示。维修策略编码后参与遗传算法的优化计算，得到优化结果后还需进行编码的逆操作−解码，解码是按照编码的方法将染色体进行对应的解释来完成的。

表2 维修方式编码

3.2 参数设置

为简化计算，规定区段长度为600 m，补偿电容个数为7。不同维修方式的影响因子1，2和3设定为0.4，0.7，1，交叉算子为0.8，变异算子为0.2，种群数目设置为200，进化代数为500，优化年限为12 a。其他参数设置如表3所示。

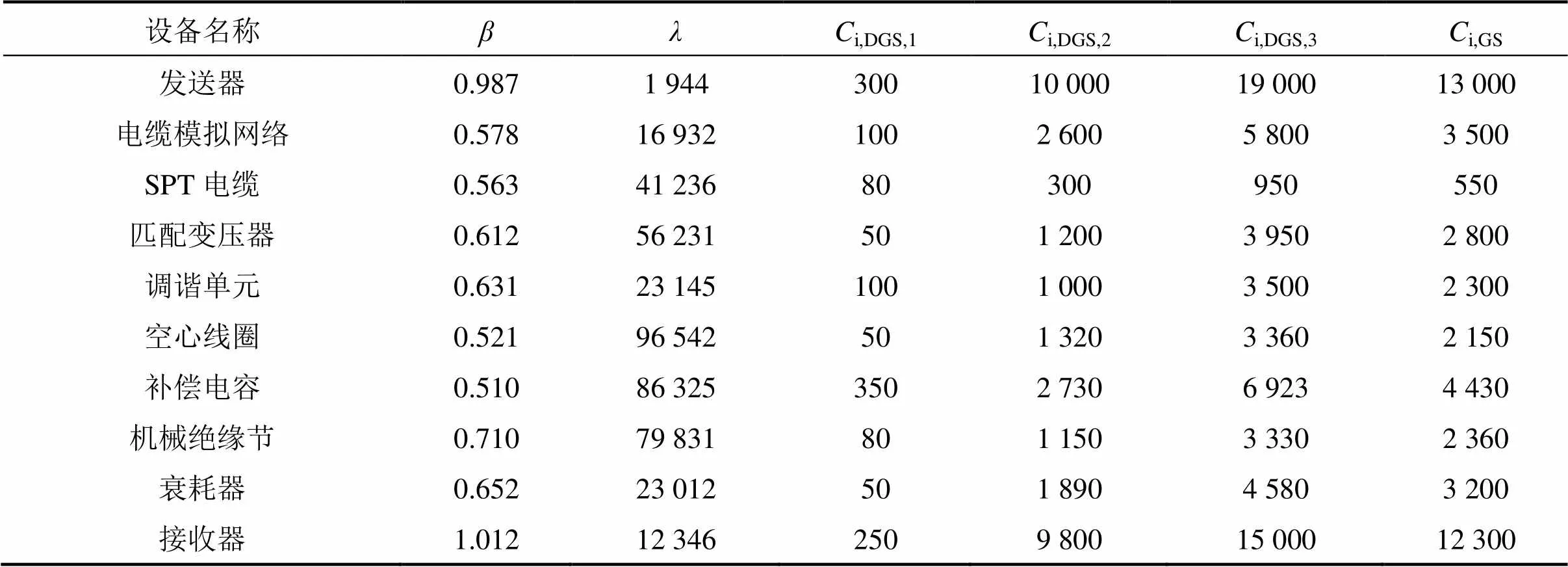
表3 系统参数

3.3 优化过程

将初始种群个体代入系统可靠性和维修费用目标函数中，得到每个个体对应的可靠度和维修费用。将带有维修信息的种群放进NSGA2算法中进行优化，最后得到Pareto最优解集。

图3为12次和16次维修次数下，优化结果对比。可以看出，随着系统平均可靠性的增加，维修费用也在不断增加，当超过一定极值后，可靠性的增加会使维修费用大幅增加。不同维修次数对可靠性和维修费用产生不同影响，当维修次数较少时，要达到较高的可靠度，维修费用会越高。维修计划的决策者可根据自身的实际情况选择合适的维修策略。以图3中A点为例，该点所对应的维修策略进行了16次维修，在优化年限12 a内，投入75万元维修费用，ZPW2000A的系统平均可靠性最低为0.785。该点所对应维修计划如表4所示。根据某铁路局某段在优化年限内的天窗维修数据及故障维修数据对其维修费用和可靠度采用本文所建模型进行计算，A策略年度累计维修成本和传统维修维修策略年度累计维修成本对比如图4所示。

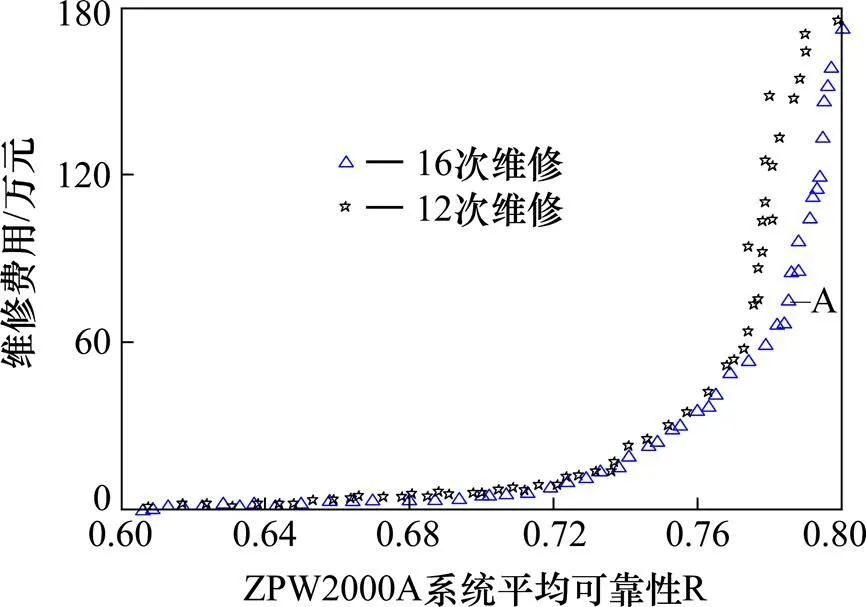
图3 不同维修次数的优化结果对比

表4 ZPW2000A维修计划

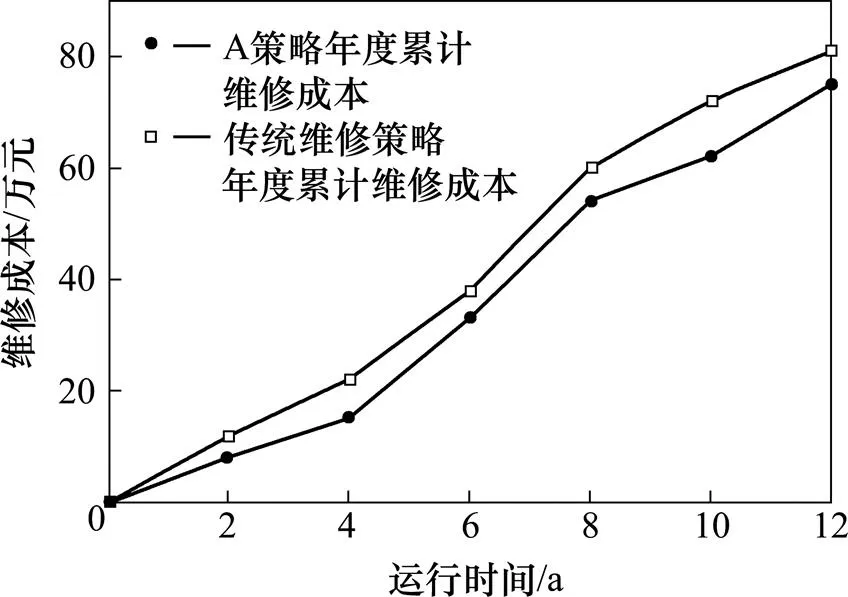
图4 2种维修策略年度累计维修成本对比图

由图4可以看出，在A维修策略下维修耗费成本低于传统维修策略。表5为在优化年限内A策略下系统可靠度和传统维修策略下系统可靠度的 对比。

表5 2种策略可靠度对比

由表5可以看出，A策略下系统可靠度优于传统维修策略。通过以上对比分析，说明本文所用优化方法得到的维修策略能够合理控制维修成本，达到的维修效果也优于传统维修策略，证明了该方法的有效性。

4 结论

1) 采用威布尔分布来描述ZPW2000A设备的失效过程，在考虑不同维修活动的条件下，利用求不交化最小路集方法对ZPW2000A系统的可靠性进行推导。为ZPW2000A可靠性领域进一步研究提供借鉴。

2) 建立以可靠性和维修费用为优化目标，以每个设备的可靠度下限为约束条件的多目标优化模型，用非劣排序遗传算法NSGA2该模型进行优化，得到的一系列最优解能为决策制定者制定合理科学的维修计划提供依据。

3) 通过对仿真结果的分析可知，通过维修使系统的可靠性增加时，所需维修成本也随之增加，超过一定极值后维修成本会大幅增加。而过高的可靠度也会要求维修次数的增加，对铁路运营和调度产生影响。因此，决策者应根据运营时间段以及其他自身实际情况选择适当的维修策略。

4) 通过与传统维修策略相比较，本文所用方法在控制维修成本和维修效果方面优于传统维修 策略。

[1] 马涛. 以可靠性为中心的ZPW-2000A无绝缘轨道电路设备维修研究[D]. 兰州: 兰州交通大学, 2013. MA Tao. Research on reliability-centered maintence of ZPW-2000A track circuit equipment[D]. Lanzhou: Lanzhou Jiaotong University, 2013.

[2] 米根锁, 张凤霞, 魏蕾. 基于剩余寿命的铁路轨道电路调整型维修方法研究[J]. 铁道学报, 2015, 37(4): 69−74. MI Gensuo, ZHANG Fengxia, WEI Lei. Research on method of modulation maintenance in railway track circuit based on residual life[J]. Journal of the China Railway Society, 2015, 37(4): 69−74.

[3] 王文斌, 苏宏升. 基于FMEA和FTA的ZPW-2000A轨道电路可靠性分析[J]. 计算机工程与应用, 2013, 49(21): 245−249. WANG Wenbin, SU Hongsheng. Analysis on reliability of ZPW-2000A track circuit based on FMEA and FTA[J]. Computer Engineering and Applications, 2013, 49(21): 245−249.

[4] 刘洪, 李荣, 葛少云, 等. 考虑出租车随机行为特性及路网行程时间可靠性的充电站多目标规划[J]. 电网技术, 2016, 40(2): 433−441. LIU Hong, LI Rong, GE Shaoyun, et al. Multiple objective planning for electric taxi charging station considering random-probability behavioral trait of taxi and travel time reliability[J]. Power System Technology, 2016, 40(2): 433−441.

[5] 肖怀硕, 李清泉, 张岩, 等. 基于非支配排序遗传改进算法的故障限流器的优化配置[J]. 电网技术, 2016, 40(8): 2444−2450. XIAO Huaishuo, LI Qingquan, ZHANG Yan, et al. Optimization of fault current limiter configuration based on improved NSGA-2[J]. Power System Technology, 2016, 40(8): 2444−2450.

[6] 姜惠兰, 安星, 王亚微, 等. 基于改进NSGA2算法的考虑风机接入电能质量的多目标电网规划[J]. 中国电机工程学报, 2015, 35(21): 5405−5411. JIANG Huilan, AN Xing, WANG Yawei, et al. Improved NSGA2 algorithm based multi-objective planning of power grid with wind farm considering power quality[J]. Proceedings of the CSEE, 2015, 35(21): 5405−5411.

[7] 王珑, 王同光, 罗源. 改进的NSGA-Ⅱ算法研究风力机叶片多目标优化[J]. 应用数学和力学, 2011, 32(6): 693−701. WANG Long, WANG Tongguang, LUO Yuan. Improved NSGA-Ⅱ in multi-objective optimization studies of wind turbine blades[J]. Applied Mathematics and Mechanics, 2011, 32(6): 693−701.

[8] 聂瑞, 章卫国, 李广文, 等. 基于Tent映射的自适应混沌混合多目标遗传算法[J]. 北京航空航天大学学报, 2012, 38(8): 1010−1016. NIE Rui, ZHANG Weiguo, LI Guangwen, et al. Adaptive chaos hybrid multi-objective genetic algorithm based on the Tent map[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(8): 1010−1016.

[9] 吕言, 刘井泉, 曾聿赟. 基于非劣排序遗传算法的核电厂维修决策多目标优化方法研究[J]. 核动力工程, 2017, 38(1): 120−125. LÜ Yan, LIU Jingquan, ZENG Yuyun. Research on multi-objective optimization method for maintenance decision of nuclear power plants[J]. Nuclear Power Engineering, 2017, 38(1): 120−125.

[10] 王晓明, 贺耀北, 李瑜, 等. 基于并行NSGA-Ⅱ算法的桥梁网络养护策略优化[J]. 土木工程学报, 2012, 45(1): 86−91. WANG Xiaoming, HE Yaobei, LI Yu, et al. Optimization of maintenance strategy for bridge networks using parallel NSGA-Ⅱ algorithm[J]. China Civil Engineering Journal, 2012, 45(1): 86−91.

[11] Kannan S, Baskar S, McCalley J D, et al. Application of NSGA-II algorithm to generation expansion planning[J]. IEEE Transactions on Power Systems, 2009, 24(1): 454− 461.

[12] Yen G, Lu H. Dynamic multiobjective evolutionary algorithm:Adative cell-based rank and density estimation[J]. IEEE Transactions on Evolutionary Computation, 2003, 7(3): 253−274.

[13] Lapa, Celso Marcelo F, Claudio Marcio NA Pereira, et al. A model for preventive maintenance planning by genetic algorithms based in cost and reliability[J]. Reliability Engineering & System Safety, 2006, 91(2): 233−240.

[14] Zio E, Bazzo R. A clustering procedure for reducing the number of representative solutions in the Pareto Front of multi-objective optimization problems[J]. European Journal of Operational Research, 2011, 210(3): 624−634.

(编辑 阳丽霞)

Research on optimization of ZPW2000A track circuit maintenance strategy based on NSGA2 algorithm

WANG Ruifeng, TAO Rongjie

(College of Automatic & Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Concerning the problem that the low reliability and high maintenance cost of traditional maintenance of ZPW2000A track circuit, the authors proposed a multi - objective optimization model of ZPW2000A maintenance strategy to optimize the maintenance strategy of ZPW2000A. In this model, the method of disjointed minimal paths was used to obtain the reliability of ZPW2000A. The influence of maintenance activities on system reliability and maintenance cost was taken into account, and the expression of ZPW2000A system reliability and maintenance cost was derived. The reliability and maintenance costs of the ZPW2000A system were considered as optimization objective and the non-inferior ranking genetic algorithm (NSGA-II) was used for calculation. It provides a variety of choices for the decision maker.Compared with the traditional method, the validity of this method was verified.

ZPW2000A; maintenance strategy optimization; disjointed minimal paths; NSGA-II; Pareto non-inferior solution set

10.19713/j.cnki.43−1423/u.2018.09.028

TP207

A

1672 − 7029(2018)09 − 2394 − 07

2017−07−02

甘肃省自然科学基金资助项目(1310RJZA046)

王瑞峰(1966−)，女，内蒙古卓资人，教授，从事交通运输自动化与控制研究；E−mail：137109066@qq.com