不同形状假设下沥青混凝土级配快速识别效果对比

高颖，郭庆林，王可意，朱涵



不同形状假设下沥青混凝土级配快速识别效果对比

高颖1，郭庆林1，王可意1，朱涵2

(1. 河北工程大学 土木工程学院，河北 邯郸 056038；2. 天津大学 建筑工程学院，天津 300072)

为提高沥青混凝土级配识别的精度，采用数字图像处理技术对沥青混凝土的平面级配进行统计分析，利用数值算法获得不同形状颗粒剖切后截面尺寸分布概率。对沥青混凝土的平面级配进行体视学转换，识别出沥青混凝土的三维真实级配，并对推测级配进行试验验证。研究结果表明：集料假设的形状不同，剖切后的截面尺寸分布概率也各不相同。采用椭球形集料假设进行体视学转换可以准确推测沥青混凝土的真实级配，避免对识别结果进行二次修正。集料的形状假设对体视学转化结果具有显著影响，建议在对平面级配进行体视学转换时采用椭球形集料假设，同时此方法亦可用于其他复合材料内部组成的定量推测。

道路工程；沥青混凝土；集料形状；级配识别；体视学转换

沥青混凝土是由矿质集料、填料、沥青和空隙组成的一种复合材料[1]。集料级配对沥青混凝土的路用性能具有重要影响[2]。因此对沥青混凝土级配的准确把握有利于控制沥青混凝土的设计施工质量，提高沥青路面的路用性能和使用寿命。传统研究中，一般采用沥青抽提的方法对沥青混合料的级配进行评价，这种方法不仅费时费力，而且操作过程相对冗繁[3]。随着数字图像处理技术的发展，数字图像处理方法逐渐被用来探究沥青混合料的级配。目前，采用数字图像方法对集料级配进行识别主要有2种方法。一种是利用集料的投影图像对集料的级配进行推测[4−5]。另一种则是利用沥青混凝土的截面图像直接评价集料的级配组成[6−7]。实际上，沥青混凝土截面图像是三维结构组成的一个局部反映，就截面中某一集料截面而言，该截面可能来自于同尺寸的集料所截得到的截面，也可能来自于更大尺寸的集料所截得到的截面，因此不同集料颗粒经过切割得到的截面之间存在一定的交叉影 响[8]，因此，吴文亮等[9−10]提出利用体视学方法对平面级配进行体视学转换，采用转换后的级配评价集料的级配组成情况。同时采用形状修正系数对结果进行修正，修正后的级配则与试验级配具有较好的一致性。可见体视学方法是一种推测沥青混凝土三维真实级配的准确方法。根据以上分析可以看出，集料形状假设会影响级配识别结果。虽然可以借助修正系数进行修正，但对集料形状的影响规律的研究还有待进一步深入。对集料形状影响规律进行分析，不仅有助于认识集料形状假设对体视学转化的影响规律，从理论层面确定合理的集料形状，对沥青混凝土级配做出快速而准确的评价。因此，本文基于不同的集料形状假设，采用数值方法研究集料形状对沥青混凝土识别级配的影响规律。

1 体视学转换方法

1.1 基本理论

工程中所用的矿质集料均为不规则的级配碎石，采用理论方法直接描述集料形状具有较大的难度，常用的做法是根据形状参数对集料进行适当简化，从而实现对集料形状的近似模拟[11]。因此，本文研究中分别将集料假设为球形、椭球形、长方体和立方体颗粒，进而分析集料形状假设对沥青混凝土级配识别结果的影响。

对于单一粒径的颗粒系统而言，若颗粒被剖切，将得到一系列不同的截面，如图1所示。

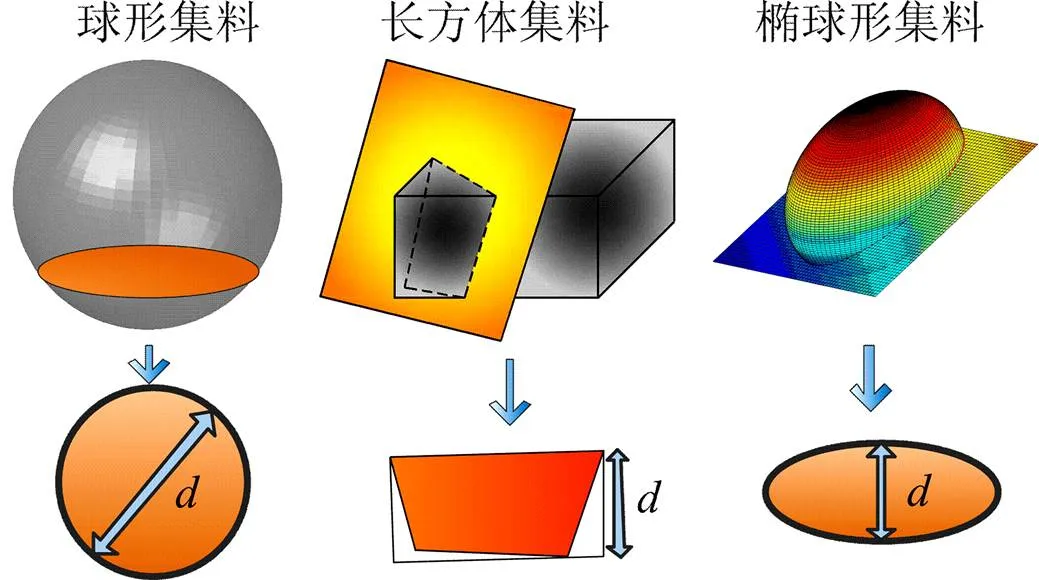
图1 不同形状颗粒切割示意图

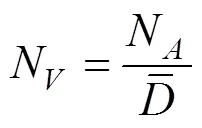
对于次大组内的颗粒截面，这些截面可能是切割本组内颗粒得到的，也可能是切割更大尺寸的颗粒得到的，因此可以得到

依此类推，便可建立如下关系

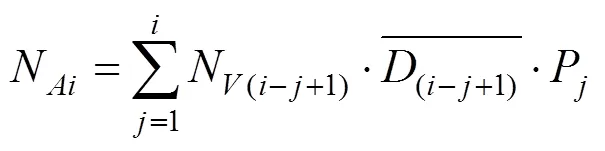
为了从沥青混凝土截面组成信息推测其三维级配组成，将式(5)改写为

1.2 颗粒截面尺寸分布概率的求解

本文根据Mora[4]提出的方法确定集料的平均厚度指数，长宽比和筛孔修正系数。由于图像采集精度限制，形状参数分析针对1.18 mm以上的颗粒进行。获得形状参数后便可以根据筛孔分组情况和集料假设确定集料尺寸。

对于球形颗粒假设，颗粒截面尺寸分布概率可以采用理论方法确定[9]。而对于椭球形、长方体和立方体颗粒则需借助数值方法求解[12]。根据筛孔尺寸和图2所示原理可以确定球形、椭球形、长方体和立方体的几何尺寸。

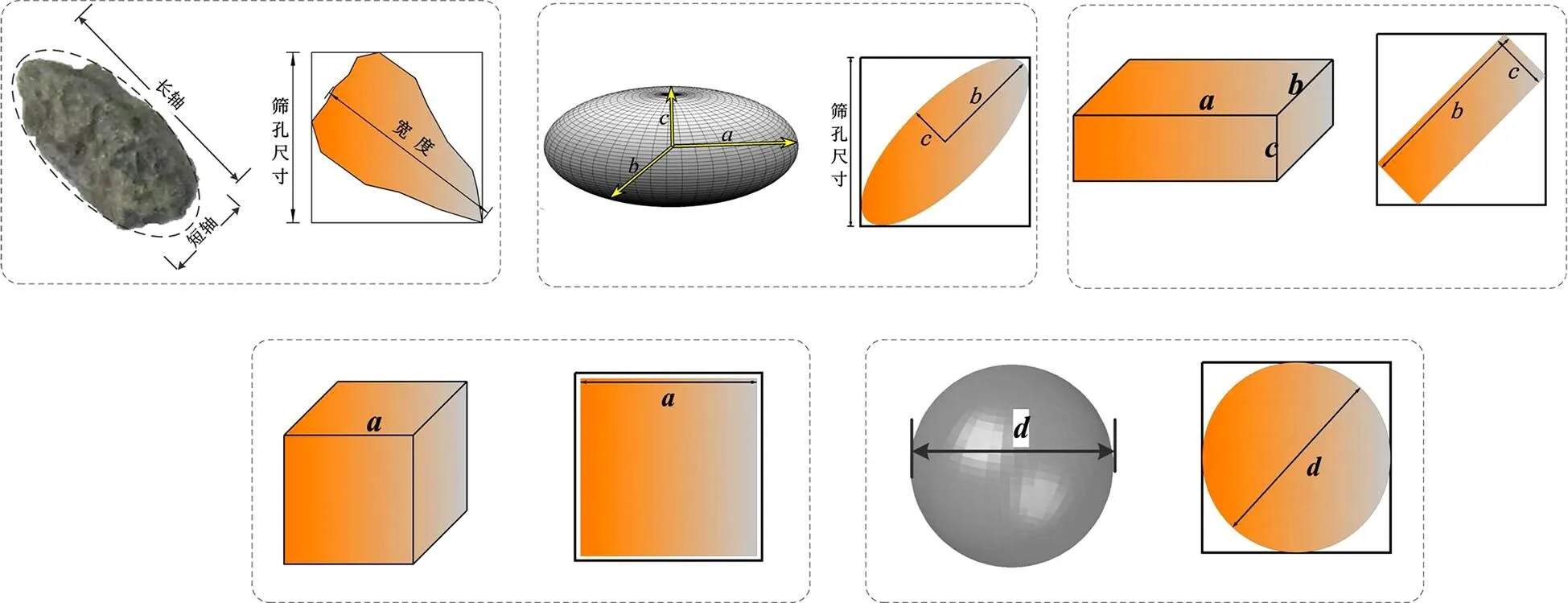
图2 不同集料过筛示意图

对于椭球颗粒，可近似采用如下关系描述筛孔尺寸，

式(7)中：为筛孔修正系数，可以通过对集料投影图像的分析获得，然后再通过厚度系数和长宽比确定其他方向的尺寸。对于长方体颗粒存在如下关系

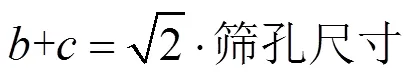
式(8)中：和为长方体的宽度和高度，通过厚度系数可以建立和之间的关系，从而确定和，再根据长宽比便可确定出长方体颗粒的长度。对于立方体和球形颗粒，可直接通过筛孔尺寸确定颗粒尺寸。运用数值程序进行颗粒剖切，通过对截面尺寸统计分析尺寸分布概率P，如式(9)所示。

2 数字图像的采集与处理

以AC-13型级配作为试验级配，选用两种不同产地的集料进行试验，制备厚度为100 mm的标准车辙板试件。按照50 mm间距对车辙板试件进行切割，锯片宽度5 mm，得到沥青混凝土截面。从所切截面中随机抽取8各截面并利用CCD数码相机获取截面图像，图像实际尺寸为300 mm×100 mm。为了获取集料参数，验证本文方法的适用性，按照现行的集料试验规程[13]称取相应质量的集料，采用CCD数码相机采集集料投影图像，如图3所示。试验共采集得到沥青混凝土截面照片8张，集料图像36张，如图4所示。按照文献[8]的图像处理方法对数字图像进行处理，采用二值图像进行级配和参数分析。对集料投影面积、外接椭圆的长、短轴进行统计分析，并以截面外接椭圆短轴作为控制尺寸，确定沥青混凝土的面积级配和每档内集料的面积数量密度。对集料面积数量密度进行体视学转换得到集料颗粒的空间数量密度，根据形状假设和试件体积可以确定每一组内集料的体积和质量，并最终确定集料级配。

图3 图像采集装置示意图

3 试验验证与分析

3.1 集料几何参数统计分析

对2种不同产地集料的投影图像进行图像处理和统计分析，得到集料的厚度指数，长宽比和筛孔修正系数，结果见表1。

表1 集料几何参数

由表1可以看出，不同产地的集料的几何参数略有不同，但没有太大变化，说明不同产地的破碎集料具有类似的形状。从两种集料的长宽比参数统计分析结果可以看出，集料实际形状并非接近球形，而呈现扁长型。因此采用球形集料假设不能准确的反映集料的实际形状，可能会导致级配识别的较大误差。

3.2 截面尺寸分布概率对比分析

为了便于求解体视学转化系数，本文采用集料几何参数平均值作为基本参数，根据前文所述方法确定颗粒尺寸。同时为了兼顾粗细集料，采用几何分组方法对集料进行分组，共分为17组，筛孔尺寸分别为16.00，11.76，8.64，6.35，4.67，3.42，2.52，1.85，1.36，1.00，0.74，0.54，0.40，0.29，0.21，0.16，0.12和0.09 mm。为了分析集料形状对截面尺寸分布概率的影响，以最大组集料为例，进行数值切割运算，得到不同形状假设下的截面尺寸分布概率，如图5所示。

图5 截面尺寸分布概率

由图5可以看出，不同形状假设下，截面尺寸分布的概率明显不同。说明集料形状假设对集料切割后得到的截面分布情况具有显著影响。立方体与球形集料切割后得到的截面尺寸分布情况大致相似。椭球形集料与长方体集料切割后得到的截面尺寸分布则存在明显差异，并且椭球形假设与球形假设下所得的概率分布情况相差较大。根据体视学理论可知，截面尺寸分布概率的差异必然会导致级配转化结果的差异性。

3.3 级配推测精度的验证

为了确定集料形状假设对沥青混凝土级配识别结果的影响，同时验证本文所提出的方法的有效性，确定最佳的形状假设，借助体视学理论和数字图像处理方法对沥青混凝土的级配进行了推测，结果如图6所示。由于本文几何分组较多，而实际所用的级配是依据筛分试验确定的，因此本文在试验级配数据基础上，根据的分组情况采用线性内插的方法确定相应的试验值。

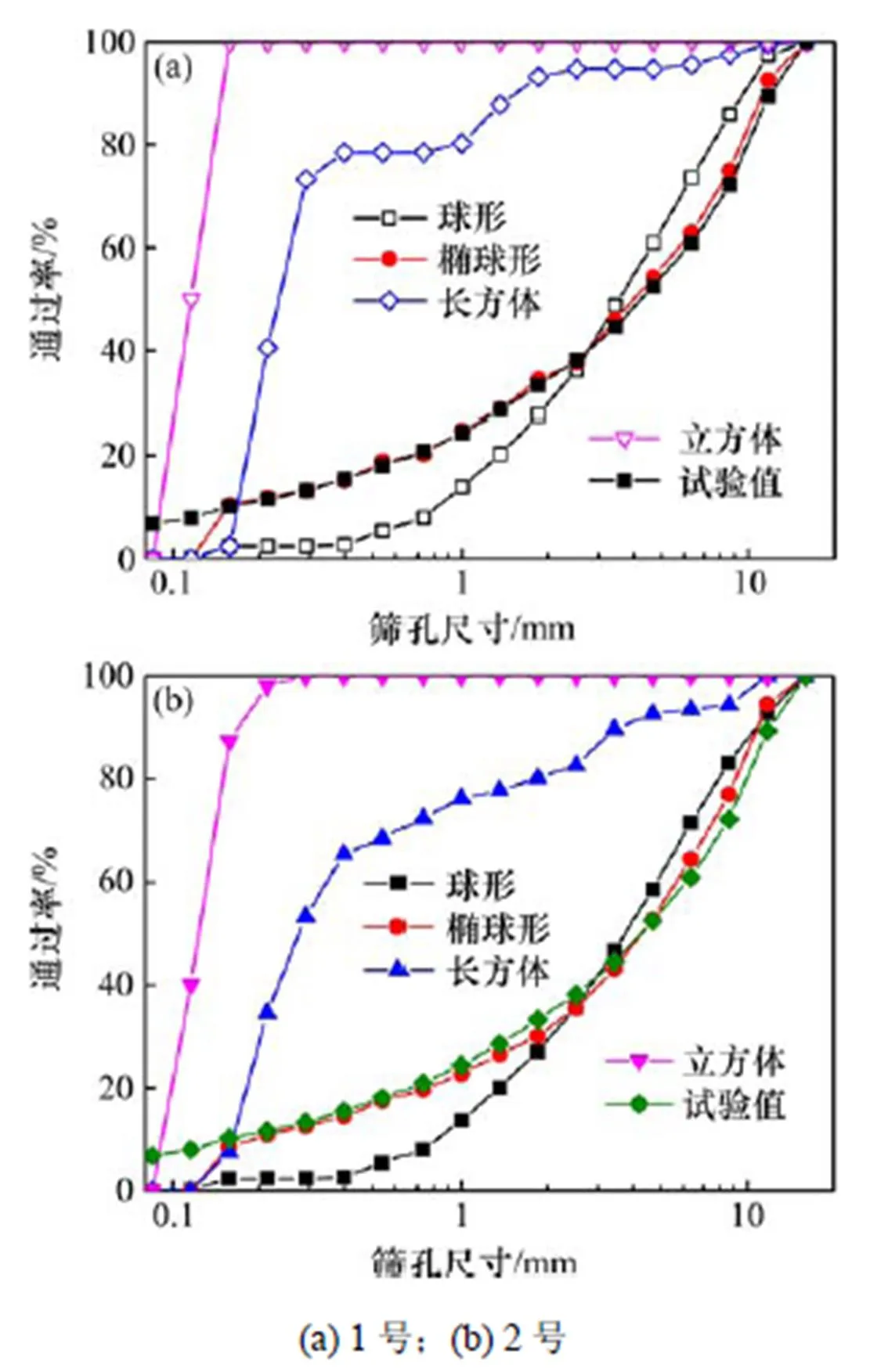
图6 级配识别结果

观察图6可以看出，集料形状假设对级配识别结果具有显著影响。其中长方体与立方体集料假设下获得的推测结果与试验结果差异巨大，说明此2种假设不能用于级配的体视学转换。球形假设与椭球形假设下获得的推测结果与试验结果较为接近，对比两种不同集料的识别结果不难发现，采用椭球形假设可以获得更准确的识别级配，此时的识别结果不需任何修正便能与试验级配基本吻合。说明在本文所探讨的情形中，椭球形集料是最宜用于体视学转换的一个集料形状。但是当集料粒径小于0.15 mm时，推测结果与试验结果则相差较大，这主要是由于受到沥青混凝土切面加工质量和图像采集精度的限制而造成的。对比图6(a)和图6(b)可以看出，对于不同集料，采用椭球形假设识别的结果均具有较好的精度，说明本文方法具有较好的稳定性和准确性。因此，在椭球形假设下，体视学转换方法能够准确推测绝大多数粗细集料的级配组成情况，同时还具备较好的适用性。

4 结论

1) 基于数字图像处理技术对集料的几何参数进行了统计分析，不同产地的破碎集料具有相似的几何形状。

2) 采用数值方法对长方体、立方体、球形和椭球形集料颗粒进行了随机切割运算，获得了切割得到的截面尺寸分布概率，分析表明集料形状对截面尺寸分布情况具有显著影响。

3) 基于不同形状集料假设，对沥青混凝土级配进行了推测。与经典的球形集料假设相比，椭球形假设能够较好的模拟不规则集料的几何特征，采用此假设进行体视学转换能够获得准确的推测结果，并且体视学转化后的结果不再需要进行修正。几何分组方法能够充分兼顾粗细集料，为细集料级配的识别提供了可能。但是对于0.15 mm以下的细集料则效果欠佳，仍有待进一步研究的深入。

4) 本文方法不仅可以用于推测沥青混凝土的三维级配组成，亦可用于其他颗粒增强复合材料，可采用此方法结合图像观测方法，定量推测复合材料的内部组成情况，具有一定的推广应用价值。

[1] 严家伋. 道路建筑材料[M]. 北京: 人民交通出版社, 2004. YAN Jiaji. Road building material[M]. Beijing: China Communications Press, 2004.

[2] 申爱琴, 蒋庆华, 祁秀林. 矿料级配对沥青混合料路用性能的影响[J]. 长安大学学报(自然科学版), 2002, 22(6): 1−4. SHEN Aiqin, JIANG Qinghua, QI Xiulin. Influence of aggregate grading on performance of asphalt mixture[J]. Journal of Chang’an University (Natural Science Edition), 2002, 22(6): 1−4.

[3] JTG E20—2011, 公路工程沥青及沥青混合料试验规程[S]. JTG E20—2011, Standard test methods of bitumen and bituminous mixtures for highway engineering[S].

[4] Mora C F, Kwan A K H, Chan H C. Particle size distribution analysis of coarse aggregate using digital image processing[J]. Cement and Concrete Research, 1998, 28(6): 921−932.

[5] 汪海年, 郝培文, 庞立果, 等. 基于数字图像处理技术的粗集料级配特征[J]. 华南理工大学学报(自然科学版), 2007, 35(11): 54−62. WANG Hainian, HAO Peiwen, PANG Liguo, et al. Investigation into grading characteristic of coarse aggregate via digital image processing technique[J]. Journal of South China University of Technology (Natural Science Edition), 2007, 35(11):54-62.

[6] Leonardo Bruno, Giuseppe Parla, Clara Celauro. Image analysis for detecting aggregate gradation in asphalt mixture from planar images[J]. Construction and Building Materials, 2012, 28(1): 21−30.

[7] Vadood M, Johari M S, Rahaei A R. Introducing a simple method to determine aggregate gradation of hot mix asphalt using image processing[J]. International Journal of Pavement Engineering, 2014, 15: 142−50.

[8] 郭庆林, 沥青混合料内部应力分布及其对粘弹性能的影响研究[D]. 长春: 吉林大学, 2013. GUO Qinglin. Research on internal stress distribution of asphalt mixture and its impact on viscoelastic performance[D]. Changchun: Jilin University, 2013.

[9] 吴文亮, 王端宜, 张肖宁, 等. 沥青混合料级配的体视学推测方法[J]. 中国公路学报, 2009, 22(5): 29−33.WU Wenliang, WANG Duanyi, ZHANG Xiaoning, et al. Stereology method of estimating gradation of asphalt mixtures[J]. China Journal of Highway and Transport, 2009, 22(5): 29−33.

[10] 黄碧霞. 体视学与图像分析技术在沥青混合料级配分析中的应用[D]. 成都: 西南交通大学, 2007.HUANG Bixia. Gradation analysis of asphalt mixture based on digital image analysis and stereology[D]. Chengdu: Southwest Jiaotong University, 2007.

[11] Dai Q, Sadd M H, You Z. A micromechanical finite element model for linear and damage-coupled viscoelastic behavior of asphalt mixture[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30: 1135−1158.

[12] Sahagian D L, Proussevitch A A. 3D particle size distributions from 2D observations: stereology for natural applications[J]. Journal of Volcanology and Geothermal Research, 1998, 84: 173−196.

[13] JTG E42—2005, 公路工程集料试验规程[S]. JTG E42—2005, Test methods of aggregates for highway engineering[S].

(编辑 涂鹏)

Comparative analysis on the fast recognized gradation of asphalt concrete under different shape assumptions

GAO Ying1, GUO Qinglin1, WANG Keyi2, ZHU Han2

(1. School of Civil Engineering, Hebei University of Engineering, Handan 056038, China; 2. School of Civil Engineering, Tianjin University, Tianjin, 300072, China)

In order to improve the recognized accuracy of gradation for asphalt concrete, the digital image processing technique was used to analyze the planar gradation statistically. The distributed probabilities of cross-section size for different particles were obtained using a numerical method. The planar gradation of asphalt concrete was converted by stereological method, a real three dimensional gradation of asphalt concrete was recognized finally, and the estimated gradation was verified with experiments. The results show that the distributed probabilities of cross-section size are different if the aggregates are assumed as different shapes. The real gradation of asphalt concrete can be estimated accurately by stereological conversion based on the assumption of ellipsoidal aggregate, this result of gradation doesn’t need to be corrected once again. When the stereological conversion is conducted, the assumed shape of aggregate has a significant impact on the converted results. It is recommended that the assumption of ellipsoidal aggregate be used for the stereological conversion on planar gradation. This method can also be used to evaluate the internal composition quantitative for other composite materials.

road engineering; asphalt concrete; aggregate shape; recognition of gradation; stereological conversion

10.19713/j.cnki.43−1423/u.2018.09.010

U414.1

A

1672 − 7029(2018)09 − 2252 − 06

2017−06−30

国家自然科学基金资助项目(51508150，51278222)；河北省高等学校青年拔尖人才计划项目(BJ2017034)；河北省自然科学基金资助项目(E2018402206)

郭庆林(1984−)，男，山东肥城人，副教授，博士，从事沥青混凝土细观损伤理论研究；E−mail：guoql@hebeu.edu.cn