高速列车作用下南京大胜关大桥动位移响应分析

赵瀚玮，丁幼亮，李爱群



高速列车作用下南京大胜关大桥动位移响应分析

赵瀚玮1，丁幼亮1，李爱群2

(1. 东南大学 混凝土及预应力混凝土结构教育部重点实验室，江苏 南京 210096；2. 北京建筑大学 北京未来城市设计高精尖创新中心，北京 100044)

基于南京大胜关大桥健康监测系统的速度监测数据，获取桥梁各部位在高速列车作用下的准静态位移响应和自由振动位移响应。讨论桥梁结构准静态位移响应、自由振动位移响应与位移动力系数的空间分布特征。建立桥梁结构在高速列车作用下的准静态位移响应、自由振动位移响应与位移动力系数概率密度模型。研究结果表明：南京大胜关大桥的主梁横向、墩顶纵向的准静态位移响应幅值与自由振动位移响应幅值存在桥梁中部(中间墩处)响应最大的空间分布特征；在长期运营过程中，南京大胜关大桥各部位单次过车的准静态位移响应服从Log-Logistic分布，自由振动位移响应服从Location-scale分布，位移动力系数服从Burr分布。

大跨钢桁拱桥；桥梁健康监测；动位移空间分布；概率密度模型

大跨钢桁架拱桥是中国高速铁路干线上的主要桥型，高速列车作用下桥梁结构的安全运营已成为土木工程界广泛关注的问题。高速列车作为大跨钢桁架拱桥运营过程中的主要激励源，桥梁结构在高速列车作用下的动位移响应是反应桥梁服役性能的重要指标。易伦雄[1]以南京大胜关长江大桥为工程背景，研究了大跨钢桁拱桥在列车荷载作用下的静动力响应以指导桥梁设计。邓子铭等[2−4]建立了大跨度铁路钢桁拱桥的车−桥耦合振动精细化分析模型，并分析了动态响应特征与其影响因素。张楠等[5]研究了京沪高速铁路南京大胜关长江大桥风—车—桥系统的耦合振动响应特征。ZHAO等[6]建立了大跨刚性系杆拱桥的精细化有限元模型，探究了各列车行车工况下大跨高速铁路拱桥刚性吊杆的静−动力学行为响应。由于位移观测时存在基准点不确定的问题，现阶段的桥梁位移响应分析大都基于有限元数值模拟，而基于实测信号的桥梁位移分析较少[7]。部分学者研究了速度信号积分成动位移信号的方法，却并未将其应用于实测数据的分析中[8−9]。本文基于南京大胜关大桥健康监测系统2015年的速度监测数据，获取了大跨钢桁拱桥各部位在高速列车作用下的准静态位移响应和自由振动位移响应。讨论了南京大胜关大桥准静态位移响应、自由振动位移响应与位移动力系数的空间分布特征。建立了南京大胜关大桥高速列车作用下的准静态位移响应、自由振动位移响应与位移动力系数概率密度模型。

1 南京大胜关大桥与结构速度响应监测

南京大胜关大桥是京沪高速铁路及沪汉蓉铁路于南京跨越长江的越江通道，并接通南京双线地铁，为六线高速铁路桥梁，正线设计行车速度300 km/h(并将在2018年提速至350 km/h)，是目前世界上设计荷载最大的高速铁路桥梁。如图1所示，南京大胜关大桥主桥长度1 272 m，采用(108＋192＋336＋336＋192＋108) m六跨连续钢桁拱结构。南京大胜关大桥全桥共设置了三联沿桥梁纵向的桁架，三联桁架之间沿横桥向相距15 m，主跨336 m钢桁拱矢高84 m，矢跨比1/4，拱顶处桁高12 m，拱脚处桁高53 m。京沪线速铁路位于下游侧，沪汉蓉铁路位于上游侧，南京地铁分列于两边桁外侧。大桥采用特制球型钢支座，中间墩的中桁设固定支座，边桁设横桥向活动支座。其他墩的中桁设顺桥向活动支座，边桁设双向活动支座。

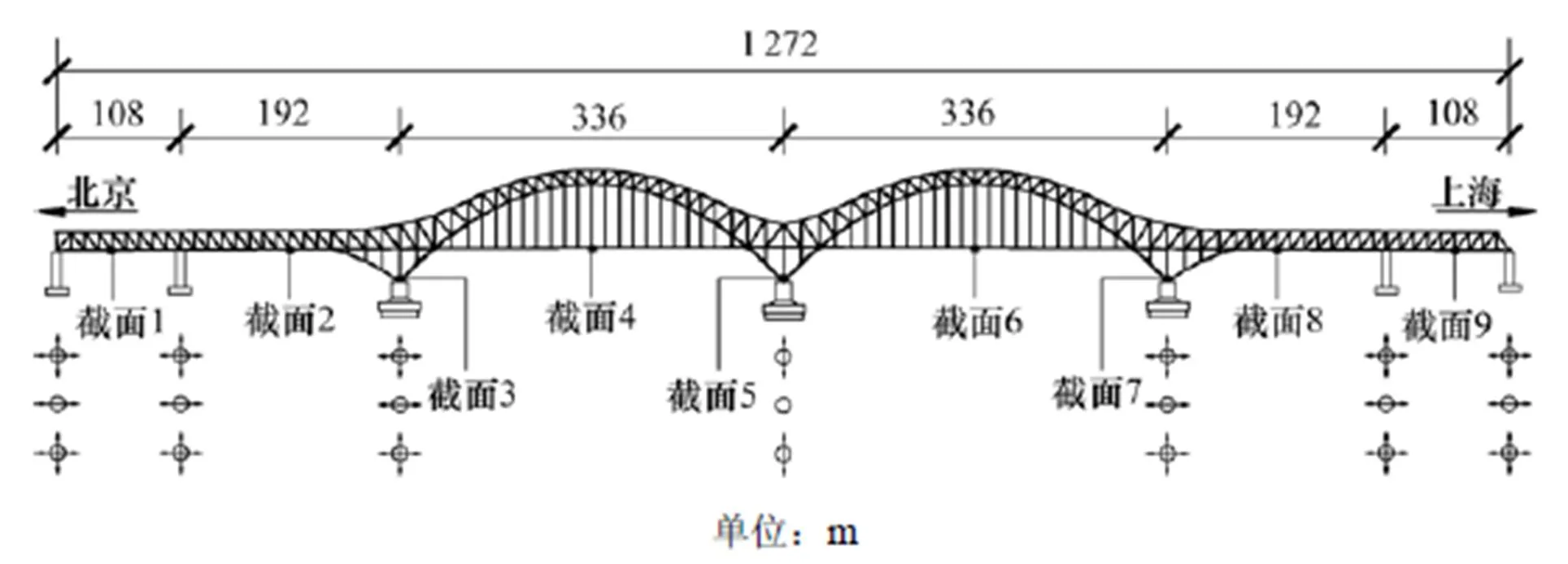
图1 南京大胜关大桥速度监测截面

鉴于南京大胜关大桥主跨跨径大、设计荷载大、列车设计时速高等特点，该桥安装了结构健康监测系统对桥梁在运营过程中的长期振动性能进行监测。南京大胜关大桥的健康监测系统安装了多个磁电式速度传感器，以采集日常服役过程中桥梁主梁与墩顶在列车作用下的速度响应。如图1和图2所示，健康监测系统中的速度监测截面一共9个：监测截面1位于北辅助跨主梁跨中，装有1个横向速度传感器(1-1)；监测截面2位于北边跨主梁跨中，装有1个横向和1个竖向速度传感器(2-2，2-3)；监测截面3位于北主跨北侧拱脚的边墩处，装有1个纵向速度传感器(3-4)；监测截面4位于北主跨主梁跨中，装有1个横向和1个竖向速度传感器(4-5，4-6)；监测截面5位于主跨拱脚的中墩处装有一个纵向速度传感器(5-7)。监测截面6~9与监测截面1~4对称布置。速度传感器采样频率为200 Hz，符合结构振动的动态测试需求。

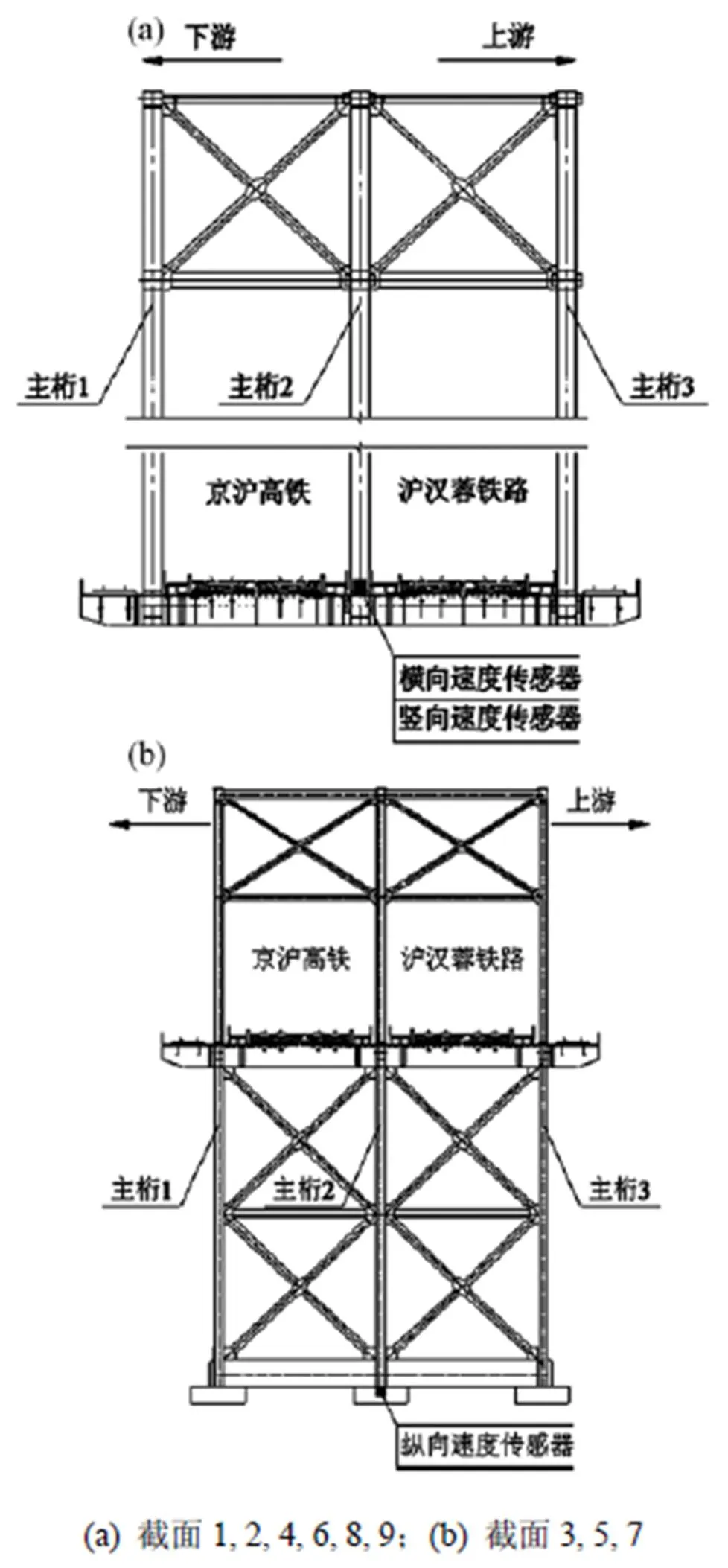
图2 监测截面速度传感器安装位置

2 基于速度监测信号的桥梁动位移响应分析方法

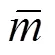
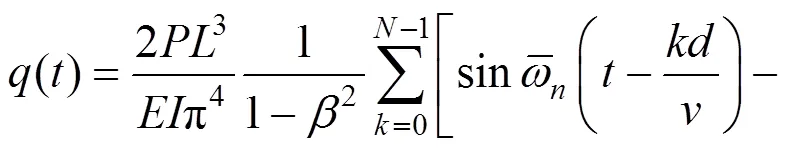
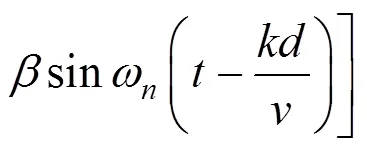
对位移响应相对于时间求一阶导数，则得到桥梁的速度响应：

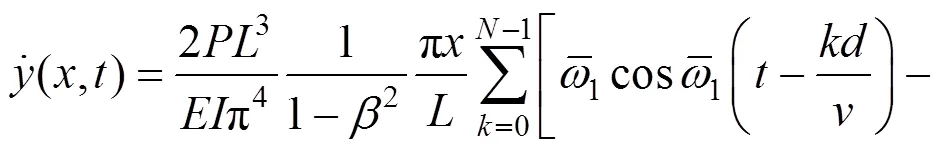
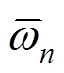
在桥梁工程中，R为桥梁结构在列车作用下的动态响应；R为列车作用下的强迫振动响应；R为列车作用下的自由振动响应，属于结构响应中的高频成分。

根据理论公式，可以制定基于速度信号的桥梁结构动位移响应工程参数获得方法如下。

采集到每次列车通过的桥梁结构速度响应后，先通过20 Hz低通滤波去除速度信号中的高频噪声[10]。采用小波包技术分离出速度响应中的强迫振动响应，将原始信号减去强迫振动响应，就得到速度响应中的自由振动响应。图3为南京大胜关大桥健康监测系统速度传感器4-6(主跨跨中主梁竖向振动响应)的典型速度响应和功率谱分析。

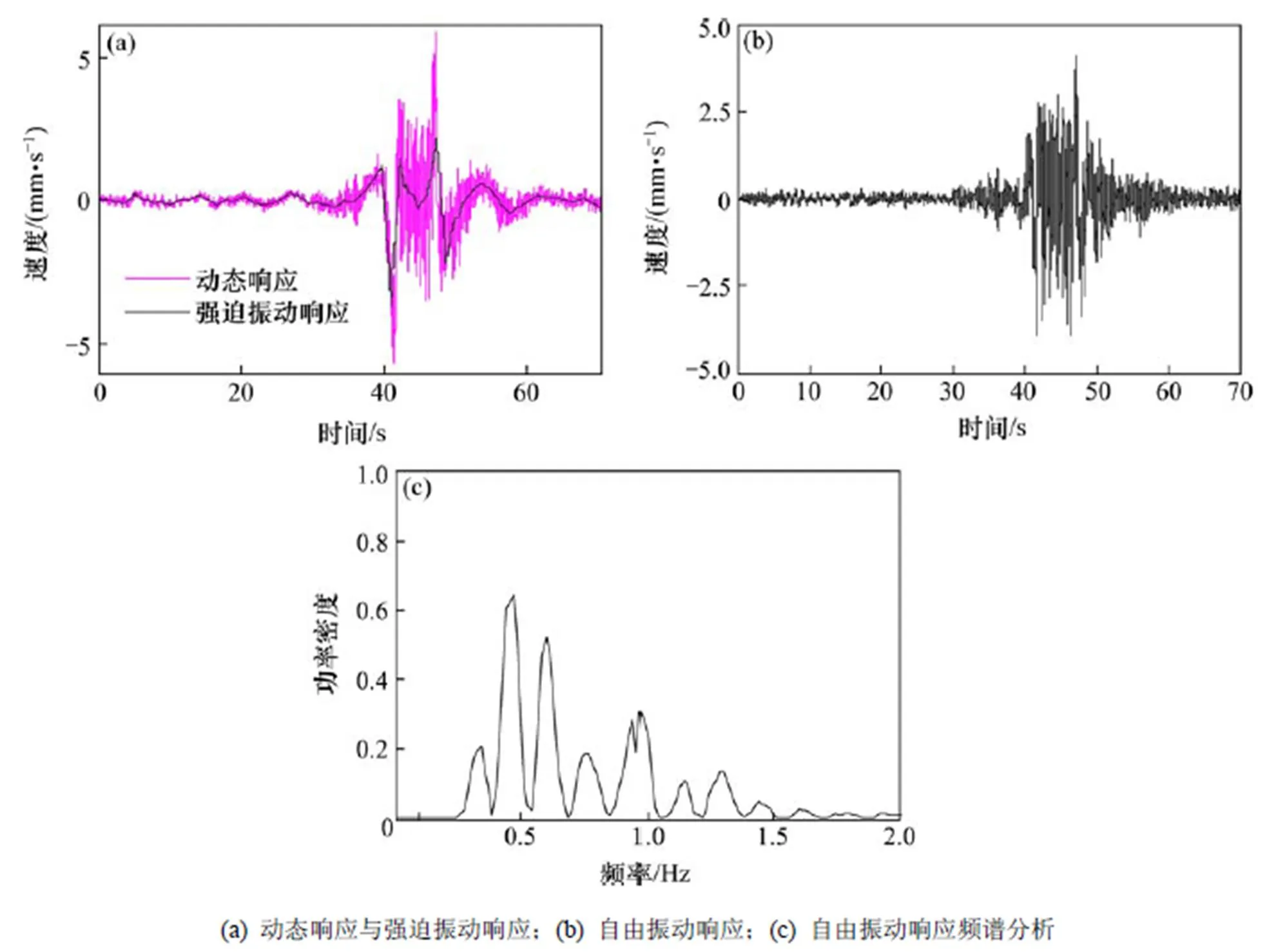
图3 传感器4-6的典型速度响应和功率谱分析

采用梯形积分方法分别对速度信号中的强迫振动响应与自由振动响应进行积分，得到桥梁结构的强迫振动位移响应(准静态位移)与自由振动位移响应。假设积分区间[,]上的速度信号函数为()，则分为等分的梯形积分公式为：

速度信号事先进行了归一化和去趋势项处理，故没有列车通过的时候，速度型号趋近于0，最大程度的避免了数值积分中积分初值不确定性的干扰。数值积分的积分初值设置为0，对强迫振动响应与自由振动响应的速度信号分别积分，可有效避免2类信号在积分过程中的相互干扰。将积分所得的准静态位移与自由振动位移相加，就得到结构的动位移响应。图4为南京大胜关大桥健康监测系统速度传感器4-6(图3中对应的速度信号)积分后的典型位移响应和功率谱分析。

图4 传感器4-6的典型位移响应和功率谱分析

从图3~4可以看出，从桥梁结构的速度响应积分到桥梁结构位移响应的过程中，准静态位移最大值相对与自由振动最大值的比值变大，结构的位移响应动力放大系数要小于速度响应的动力放大系数。另外，从速度自由振动响应的频谱分析和位移自由振动响应的频谱分析结果中可以看出，积分过程有效保留了结构的前几阶固有频率的振动成分，监测信号自由振动的固有频率结果与有限元分析相符合[6]。

以每次列车通过的动位移时程曲线峰值除以准静态位移时程曲线峰值(如图4(a))，就可以得到桥梁工程中的另一个重要参数，即动力系数，动力系数通常被定义为：结构动态响应最大值与结构拟静态响应最大值的比值[11]。动力系数的表达式可定义为：

式中：dmax为单次过车的动态位移最大值；smax为单次过车的准静态位移最大值。

3 桥梁动位移响应与空间分布特征

计算2015年全年南京大胜关大桥各个传感器在每次列车通过时的准静态位移最大值和自由振动最大值，就可以分析桥梁各个部位的车致动位移的响应特征。表1中所列的是由2015年南京大胜关大桥各个传感器的每次列车通过时的准静态位移最大值，自由振动位移最大值，位移动力系数所得的全年均值。从表1可以看出：高速列车作用下，南京大胜关大桥各个部位单次过车的准静态位移响应幅值相比其自由振动幅值要大得多，桥梁的墩顶纵向位移响应相对桥梁的主梁横向、竖向位移响应要更大，桥梁的竖向位移响应的动力系数值比纵向位移响应与横向位移响应大。

表1 各传感器位移响应最大值与位移动力系数全年均值

根据表1的结果就可以得到2015年全年各个部位每次过车的准静态位移最大值、自由振动位移最大值、位移动力系数的全年均值沿桥梁纵向的分布特征。分布特征采用分段3次Hermite插值多项式进行回归和分析。图5(a)为各个部位每次过车的准静态位移最大值全年均值的空间分布特征，图5(b)为各个部位每次过车的自由振动位移最大值全年均值的空间分布特征，图5(c)为各个部位每次过车的位移动力系数全年均值的空间分布特征。

从图5可以看出，高速列车作用下：

1) 南京大胜关大桥各个部位的主梁横向准静态位移响应幅值、墩顶纵向准静态位移响应幅值存在明显的纵向空间分布特征，桥梁中部(中间墩处的主梁与墩顶)的准静态位移响应响应最大。主梁竖向准静态位移响应幅值沿桥长相对稳定。

2) 南京大胜关大桥各个部位的主梁横向自由振动位移响应幅值、主梁竖向自由振动位移响应幅值、墩顶纵向自由振动位移响应幅值存在明显的纵向空间分布特征。桥梁中部(中间墩处的主梁与墩顶)的横向与纵向自由振动响应最大。桥梁主跨的主梁的竖向自由振动相比边跨与辅助跨的主梁更为 剧烈。

3) 南京大胜关大桥各个部位的主梁横向位移动力系数、主梁竖向位移动力系数不存在明显的纵向空间分布特征。桥梁墩顶纵向位移的动力系数在中间墩的数值最大，在边墩处相对较小。

可以看出，不论是准静态位移响应、自由振动位移响应、还是位移动力系数响应值，它们的空间分布规律大都呈现桥梁中部(中间墩处)响应值最大。这与一般桥梁设计规则中，响应最大值出现在桥梁主跨跨中的理念大不相同。

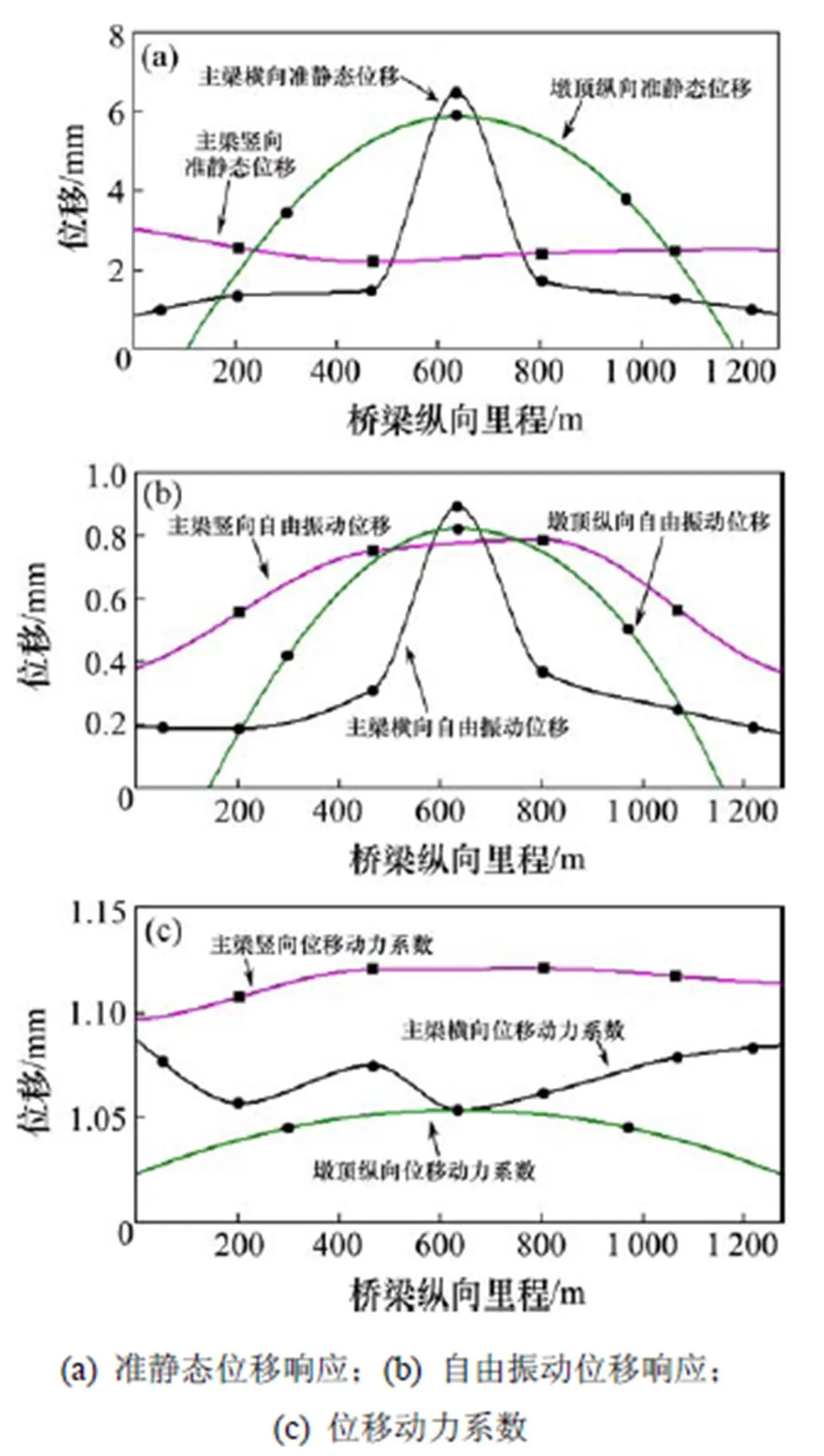
图5 桥梁位移响应最大值与动力系数全年均值空间分布特征

4 桥梁动位移响应的概率密度模型

南京大胜关大桥在运营过程中受到高速列车的长期作用。要想准确把握桥梁结构在高速列车作用下的长期振动性能，就必须对桥梁各部位的车致响应进行概率特征分析。基于2015年全年单次过车的准静态位移最大值、自由振动位移最大值与位移动力系数的概率分布特征，就可获得桥梁各部位的车致位移响应的长期特征。基于桥梁各部位的准静态位移的概率直方图分布特征，选用Log-Logistic分布来描述桥梁准静态位移的概率密度统计特性，其函数表达式为：

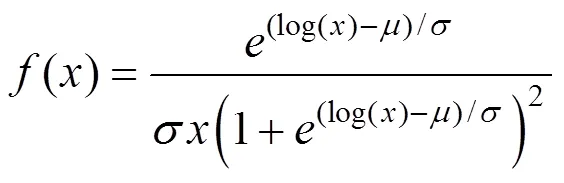
式中：为log()的均值；为log()的标准差，两者分别是表征位置和尺度的参数。基于桥梁各部位自由振动位移的概率直方图分布特征，选用Location-scale分布来描述桥梁自由振动位移的概率密度统计特性，其函数表达式为：

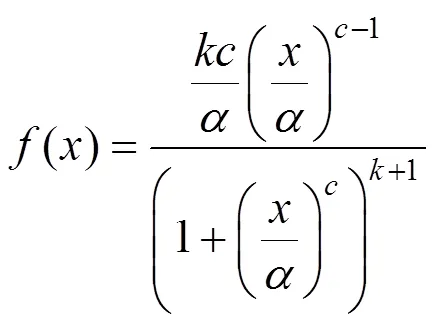
式中：，和分别是尺度参数、形状参数1和形状参数2。

图6~7分别为传感器4-5(主跨跨中主梁横向振动响应)与传感器4-6(主跨跨中主梁竖向振动响应)的准静态位移最大值、自由振动位移和位移动力系数概率分布直方图与概率密度拟合曲线。

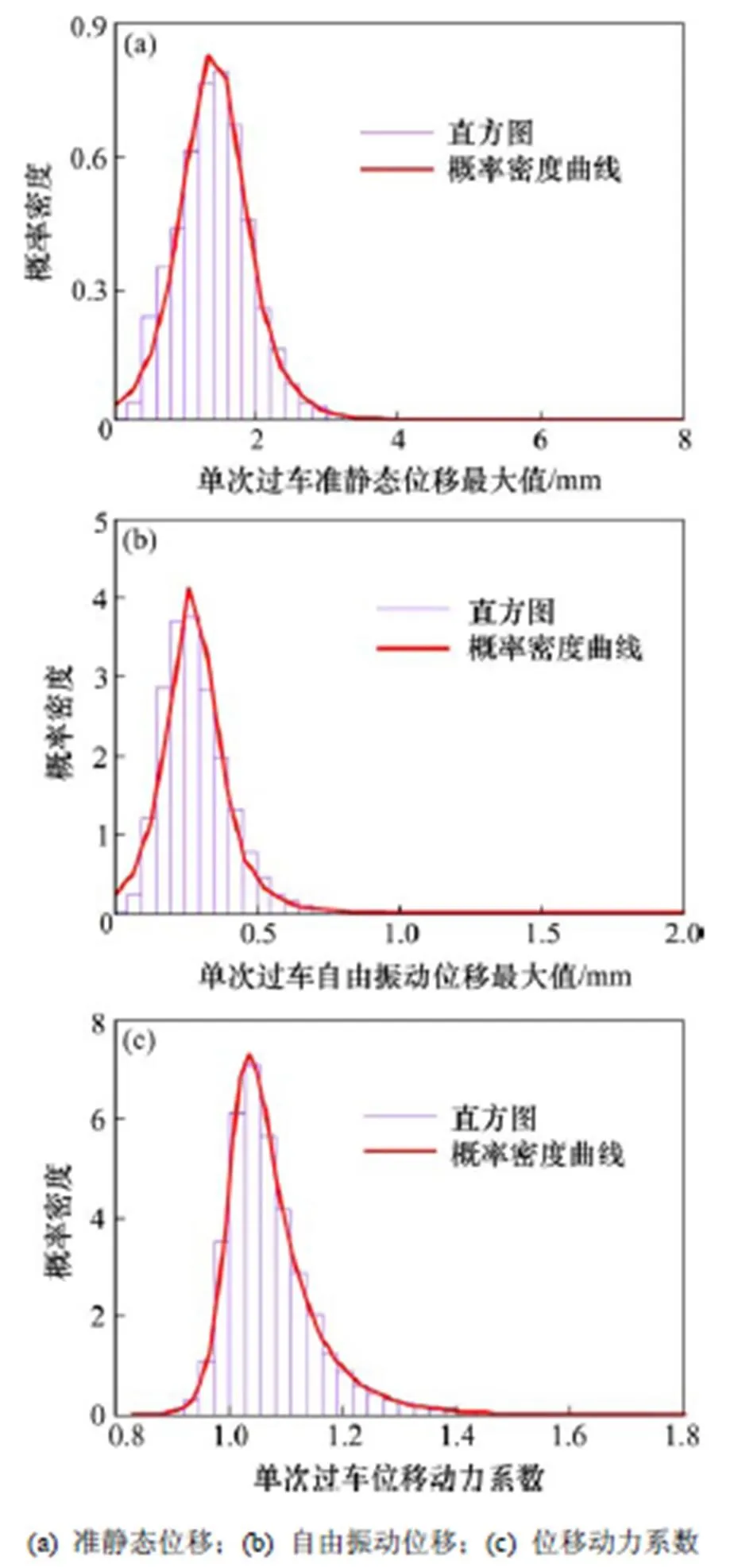
图6 传感器4-5全年单次过车位移响应概率特征

从图6~7可以看出：在1 a的运营时间中，南京大胜关大桥各部位单次过车的准静态位移响应，自由振动位移响应、位移动力系数均从一定的概率模型分布。其中，准静态位移响应服从Log-Logistic分布，自由振动位移服从t Location-scale分布，位移动力系数服从Burr分布。

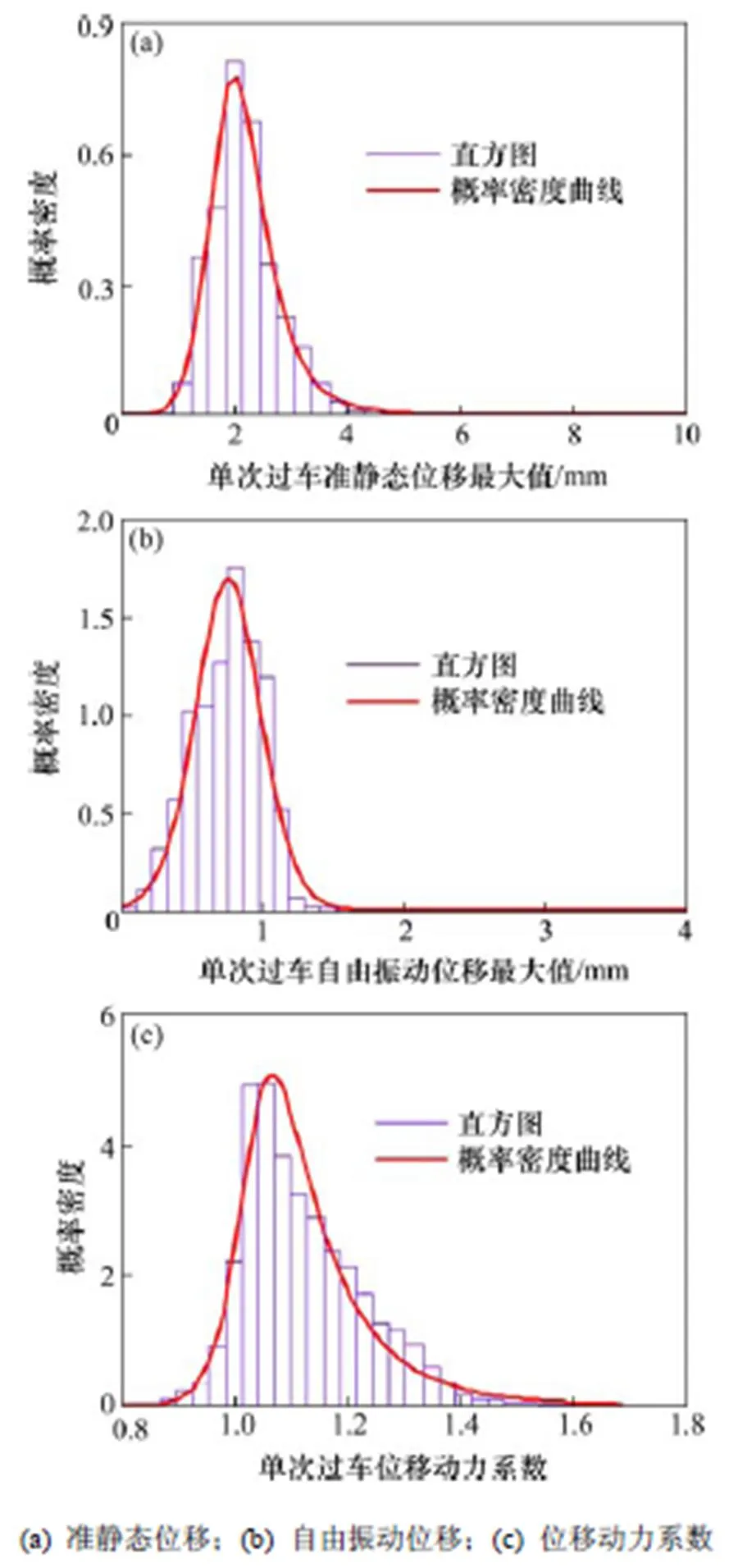
图7 传感器4-6全年单次过车位移响应概率特征

5 结论

1) 高速列车作用下，南京大胜关大桥各个部位的主梁横向准静态位移响应幅值、墩顶纵向准静态位移响应幅值存在明显的纵向空间分布特征，桥梁中部(中间墩处的主梁与墩顶)的准静态位移响应幅值最大。南京大胜关大桥各个部位的主梁横向自由振动位移响应幅值、主梁竖向自由振动位移响应幅值、墩顶纵向自由振动位移响应幅值存在明显的纵向空间分布特征，桥梁中部的横向与纵向自由振动位移响应最大，桥梁主跨的主梁的竖向自由振动相比边跨与辅助跨的主梁更为剧烈。南京大胜关大桥墩顶纵向位移的动力系数在中间墩的数值最大，在边墩处相对较小。

2) 在桥梁的长期运营过程中，南京大胜关大桥各部位单次过车的准静态位移响应、自由振动位移响应、位移动力系数均从一定的概率模型分布。其中，准静态位移响应服从Log-Logistic分布，自由振动位移响应服从t Location-scale分布，位移动力系数服从Burr分布。

[1] 易伦雄. 南京大胜关长江大桥大跨度钢桁拱桥设计研究[J]. 桥梁建设, 2009(5): 1−5. YI Lunxiong. Design and study of long span steel truss arch bridge of Dashengguan Changjiang River Bridge in Nanjing[J]. Bridge Construction, 2009(5): 1−5.

[2] 邓子铭, 郭向荣, 唐俊峰. 三主桁梁桥车桥耦合振动分析[J]. 噪声与振动控制, 2010(6): 9−12. DENG Ziming, GUO Xiangrong, TANG Junfeng. Vehicle-bridge coupled vibration analysis for a three- principal-trusses arch-bridge[J]. Noise and Vibration Control, Noise and Vibration Control, 2010(6): 9−12.

[3] 蒲黔辉, 魏召兰, 李晓斌. 大跨连续钢桁拱桥动力系数影响因素研究[J]. 地震工程与工程振动, 2011, 31(6): 123−128. PU Qianhui, WEI Zhaolan, LI Xiaobin. Study on dynamic coefficient influence factors of continuous steel truss arch bridge with large span[J]. Journal of Earthquake Engineering and Engineering Vibration, 2011, 31(6): 123−128.

[4] 张敏. 大跨度铁路钢桁拱桥车−桥耦合振动分析[J]. 桥梁建设, 2012, 42(6): 14−19. ZHANG Min. Analysis of train-bridge coupled vibration of long span railway steel truss arch bridge[J]. Bridge Construction, 2012, 42(6): 14−19.

[5] 张楠, 夏禾, 郭薇薇, 等. 京沪高速铁路南京大胜关长江大桥风—车—桥耦合振动分析[J]. 中国铁道科学, 2009, 30(1): 41−48. ZHANG Nan, XIA He, GUO Weiwei, et al. Analysis on the wind-vehicle-bridge coupling vibration for Nanjing Dashengguan Yangtze River Bridge of Beijing-Shanghai high-speed railway[J]. China Railway Science, 2009, 30(1): 41−48.

[6] ZHAO H W, DING Y L, AN Y H, et al. Transverse dynamic mechanical behavior of hangers in the rigid tied-arch bridge under train loads[J]. Journal of Performance of Constructed Facilities-ASCE, 2017, 31(1): 1−16.

[7] WANG Gaoxin, DING Youliang, SONG Yongsheng, et al. Detection and location of the degraded bearings based on monitoring the longitudinal expansion performance of the main girder of the Dashengguan Yangtze bridge[J]. Journal of Performance of Constructed Facilities-ASCE, 2016, 30(4): 1−10.

[8] 吴康雄, 张红光. 桥梁动挠度计算速度积分方法[J]. 长沙理工大学学报(自然科学版), 2009, 6(1): 15−18. WU Kangxiong, ZHANG Hongguang. The calculation of dynamic deflection from bridge measuring velocity[J]. Journal of Changsha University of Science and Technology (Natural Science), 2009, 6(1): 15−18.

[9] 林楠, 李东升, 李宏男. 基于零初值的测试加速度积分速度与位移的方法[J]. 中国科学: 技术科学, 2016, 46(6): 602−614. LIN Nan, LI Dongsheng, LI Hongnan. Novel integration method of measured acceleration to velocity and displacement based on zero initial condition[J]. Scientia Sinica Technologica, 2016, 46(6): 602−614.

[10] TB 10621—2014, 高速铁路设计规范[S]. TB 10621—2014, Code for design of high speed railway[S].

[11] TB 10415—2003, 铁路桥涵检定规范[S]. TB 10415—2003, Code for rating existing railway bridges[S].

(编辑 蒋学东)

Analysis of the dynamic displacement responses of the Nanjing Dashengguan Bridge under high-speed trains

ZHAO Hanwei1,DING Youliang1,LI Aiqun2

(1. Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China; 2. Beijing Advanced Innovation Center for Future Urban Design, Beijing University of Civil Engineering and Architecture, Beijing 100044, China)

Based on the long-term monitoring data of velocity on the structural health monitoring system of the Nanjing Dashengguan Bridge, the quasi-static displacement and free vibrating displacement of various bridge parts were obtained. The features of spatial distribution of train-induced quasi-static displacement, free vibrating displacement and displacement dynamic load factor (DLF) of the bridge structure were discussed. The model of probability density of train-induced quasi-static displacement, free vibrating displacement and displacement DLF of the bridge structure were established. The main conclusions obtained are as follows: The horizontal quasi-static displacement and free vibrating displacement of beam, the longitudinal of quasi-static displacement and free vibrating displacement of the pier top, obey the principle that the largest values occur at the center of the bridge (near the mid-pier) along the longitudinal direction; in the long-term operation of the bridge, the quasi- static displacements of each train passing obey the Log-Logistic distribution, the free vibrating displacements obeyLocation-scale distribution, and the displacement DLFs obey the Burr distribution.

long-span steel-truss arch bridge; structural health monitoring; spatial distribution of dynamic displacement responses; model of probability density

10.19713/j.cnki.43−1423/u.2018.09.001

U448.13；U448.224

A

1672 − 7029(2018)09 − 2187 − 09

2017−07−03

国家重点基础研究发展计划(973计划)资助项目(2015CB060000)；国家自然科学基金资助项目(51438002，51578138)；东南大学优秀博士学位论文培育基金资助项目(YBJJ1657)；中央高校基本科研业务费专项资金与江苏省普通高校研究生科研创新计划资助项目(KYLX16_0251)

丁幼亮(1979−)，男，江苏苏州人，研究员，博士，从事结构健康监测和防灾减灾研究；E−mail：civilding@163.com