混凝土-CA砂浆复合试件界面端奇异应力场消除方法研究

曹世豪，李佳莉，康维新，刘学毅



混凝土-CA砂浆复合试件界面端奇异应力场消除方法研究

曹世豪，李佳莉，康维新，刘学毅

(西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031)

为研究混凝土-CA砂浆双材料界面端的应力场奇异性，建立混凝土-CA砂浆双材料复合试件轴拉计算模型，并对界面拉应力分布进行分析。基于Bogy特征方程，提出消除混凝土-CA砂浆复合试件界面端奇异性的方法。研究结果表明：混凝土与CA砂浆界面端附近存在应力奇异现象，该应力奇异现象使得界面端点处的应力明显增加。当结合角组合1=2≤72°时，混凝土-CA砂浆界面端的应力奇异性消失，此时应力场为一定值。研究成果可为精确的双材料界面黏结强度试验提供理论依据。

板式无砟轨道；双材料界面端；应力奇异性；Bogy特征方程；结合角组合

CRTSⅡ板式无砟轨道作为典型的层状结构，其层间界面破坏较为严重[1−2]，如图1所示。研究多认为导致层间破坏的外因为较大的列车和温度荷载，而内因是层间作为薄弱环节，其黏结强度不 足所致[3−6]。事实上，由于混凝土和CA砂浆2种材料性能的不同，会在界面端(图2中点)附近产生奇异应力场。该奇异应力场可能是导致层间界面裂纹萌生和扩展的深层次原因，也是造成无法准确测量界面黏结强度的一个重要原因。针对双材料界面端应力奇异性的问题，Bogy等[7−9]利用Mellin变换提出双材料界面端具有应力奇异性的观点。Kubo等[10]利用Airy的应力函数，求得了应力奇异次数为实数时的奇异应力场和位移场。考虑到应力奇异次数也可能为复数，许金泉等[11]利用弹性力学中的Goursat公式，推导出具有任意结合角的双材料界面端附近的奇异应力场和位移场，且所得出的应力奇异性特征方程与Bogy利用Mellin变换求得的结果完全一致。本文基于Bogy特征方程和有限单元法，提出消除混凝土和CA砂浆界面端应力奇异性的方法，并设计出避开混凝土-CA砂浆界面端奇异性的黏结强度试验方案。研究成果可为混凝土-CA砂浆界面黏结强度试验提供理论依据。

图1 CRTSⅡ板式无砟轨道双材料界面裂缝

1 双材料界面端应力奇异性的指数特征方程

对于由2种材料构成的双材料结构，Bogy采用Melin变换给出了任意接合角组合(1，2)条件下界面端(点)附近应力奇异性指数的特征方程[9, 11−12]：

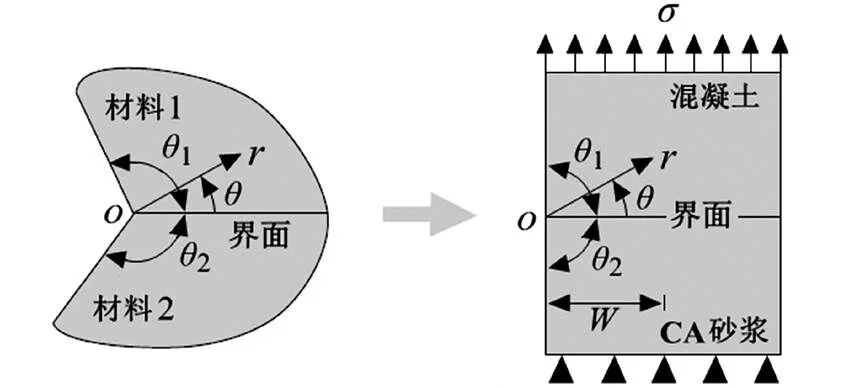
图2 双材料界面端几何模型

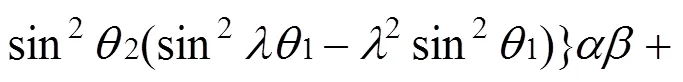
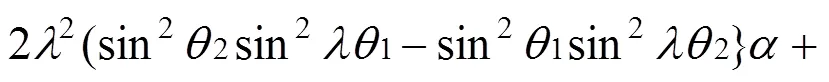
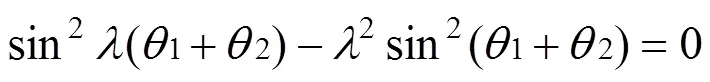
式中：1和2为两接合角(见图2)，λ为表征界面端应力场强度的应力奇异性指数；和为Dundurs材料参数[8]：

E和v(=1, 2)为材料的弹性模量和泊松比，对于平面应力问题，有：

对于平面应变问题，有：

2 双材料界面端应力奇异性的存在性

针对双材料界面的黏结强度，水工混凝土试验规程SL 352—2006建议采用图3所示的试件，通过单轴拉伸获取极限拉力，以平均应力作为界面黏结抗拉强度[13]。实际上，无砟轨道层间作为双材料界面，由于其端部应力奇异效果，使得在轴向拉伸时，界面端部应力往往要比平均应力大得多。

为证实双材料界面端存在应力场奇异性，以CRTSⅡ型板式无砟轨道的为例，计算界面的拉应力分布。其中C15，C30，C55混凝土和CA砂浆的弹性模量和泊松比如表1所示；计算模型的有限元网格如图4所示。

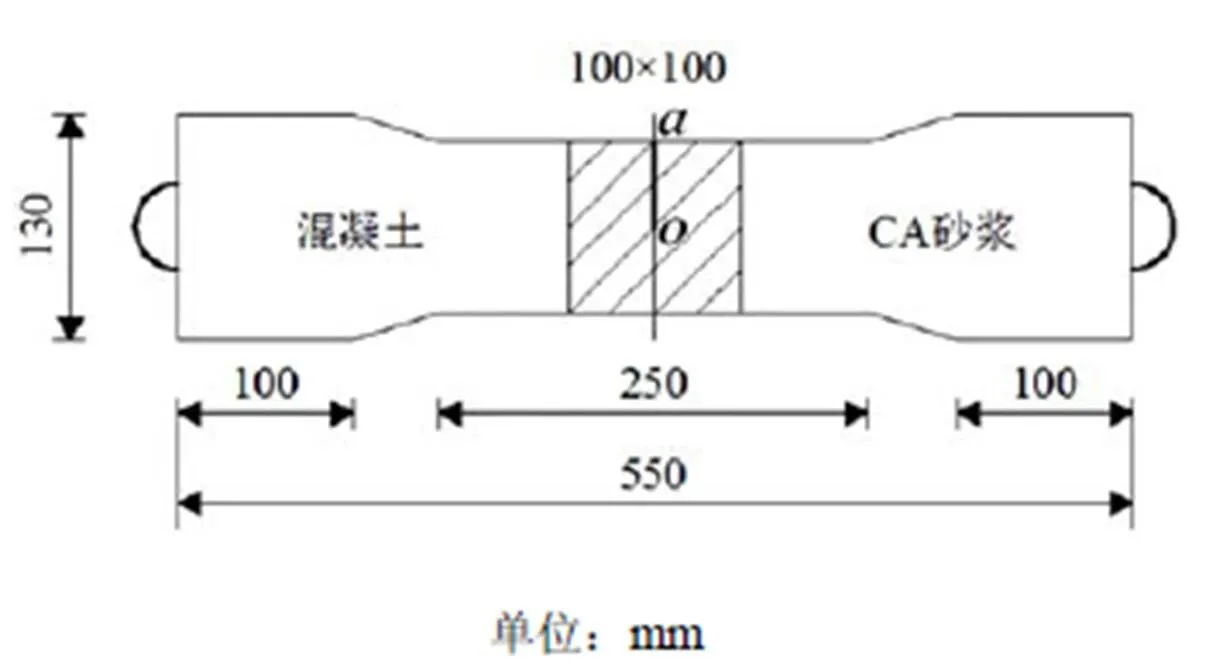
图3 双材料复合试件尺寸

图4 双材料复合试件有限元模型

由图5可知：当界面两侧材料相同时(均为混凝土)，界面拉应力分布比较均匀，而当界面两侧材料不一致时(左侧为混凝土，右侧为CA砂浆)，界面应力分布不再均匀，其中界面端的应力明显大于其他区域，即该处应力呈现奇异性。

图5 材料差异对界面拉应力分布的影响(沿着图3中oa线)

图6 单元尺寸对界面端拉应力的影响

为了进一步确定界面端应力场的奇异性，分别对单材料界面端(混凝土−混凝土)和双材料界面端(混凝土-CA砂浆)的应力进行分析，结果如图6所示。从图中可知：当试件为单材料时，界面端的应力为一定值1 Pa，且该值不随单元尺寸的变化而改变，这与理论计算结果较为一致，也表明有限元模型的单元尺寸精度是足够的。而对于双材料界面端，其界面端应力随着单元尺寸的减小而呈增加趋势，表现出明显的奇异性特征。因此，由于双材料界面端应力场存在奇异性，使得通过试验方法确定界面黏结强度时，首先需要先消除界面端应力场的奇异性，使得界面端应力为一定值。

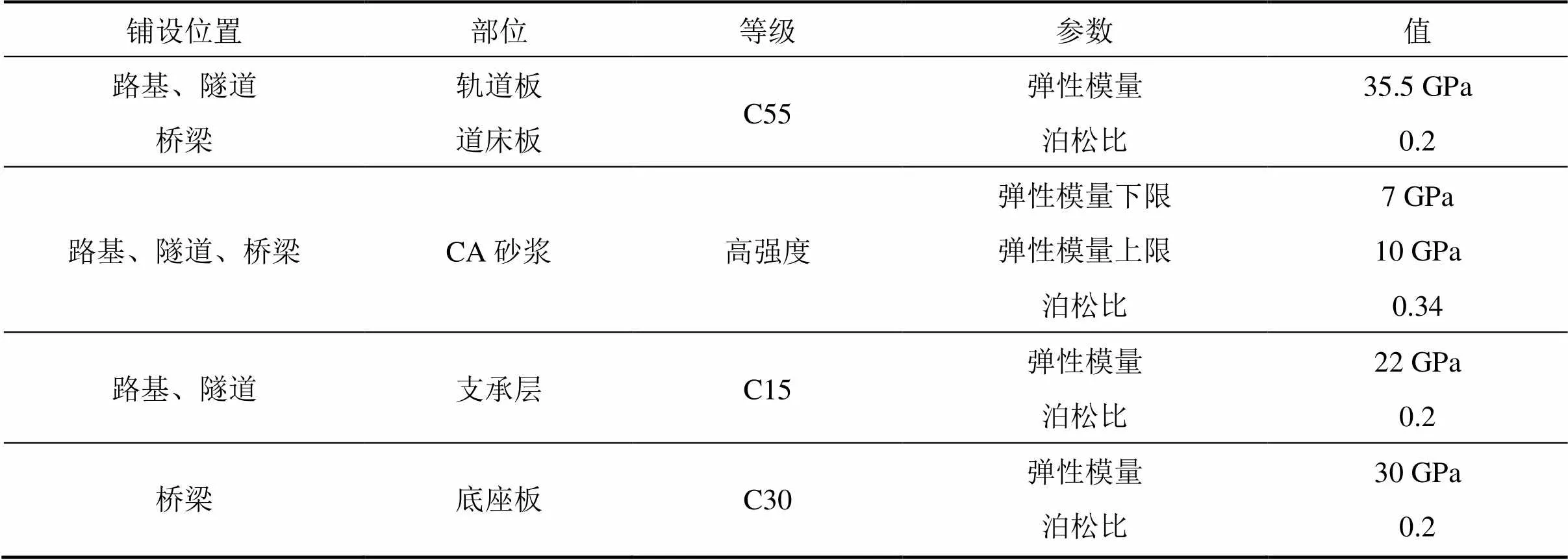
表1 材料参数[14−15]

3 双材料界面端应力奇异性的消除方法

对于双材料界面端应力场奇异性，由Bogy特征方程不难发现，对于确定的材料组合和，通过改变结合角1和2的值，可以达到消除界面端应力奇异性的目的。

依据上述方法，针对CRTSⅡ板式无砟轨道混凝土与CA砂浆的双材料界面端，求得在0°≤(1，2)≤180°范围内，不存在应力奇异性的结合角组合，如图7所示。图7中曲线表明的是消除应力奇异性的角度组合上限值，实际上，位于曲线下方的任意角度组合都可以消除界面端的应力奇异性。

图7 无应力奇异性结合角组合曲线

由图7可知，对于C15-CA砂浆组成的双材料结构，当1=2=68.50°(=1.6，参考图8)、1=2= 72.06°(=1.5)时的界面端点属于无应力奇异区，而当1=2=75.63°(=1.4)，1=2=79.21° (=1.3)，1=2=90°(=)时的界面端属于应力奇异区。为了进一步验证此现象，采用图8的计算模型，针对不同的试件尺寸=，1.1，1.2，1.3，1.4，1.5和1.6，分别对C15-C15，C15-CA，C30-C30，C30-CA，C55-C55和C55-CA等工况进行计算，如表2所示，获取界面的拉应力(σ)分布如图9~11 所示。

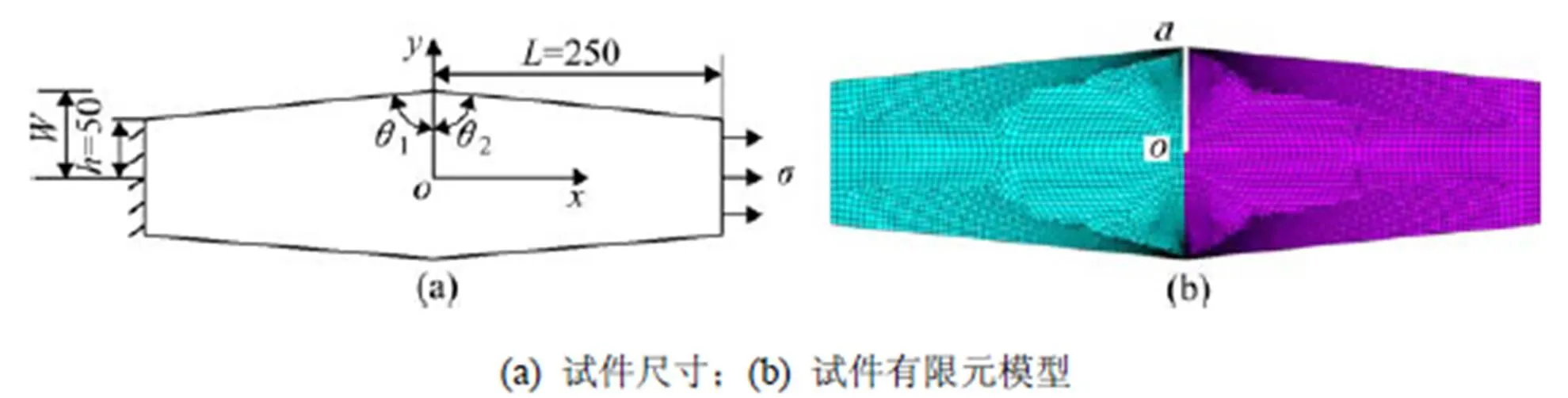
图8 双材料复合试件尺寸及有限元模型

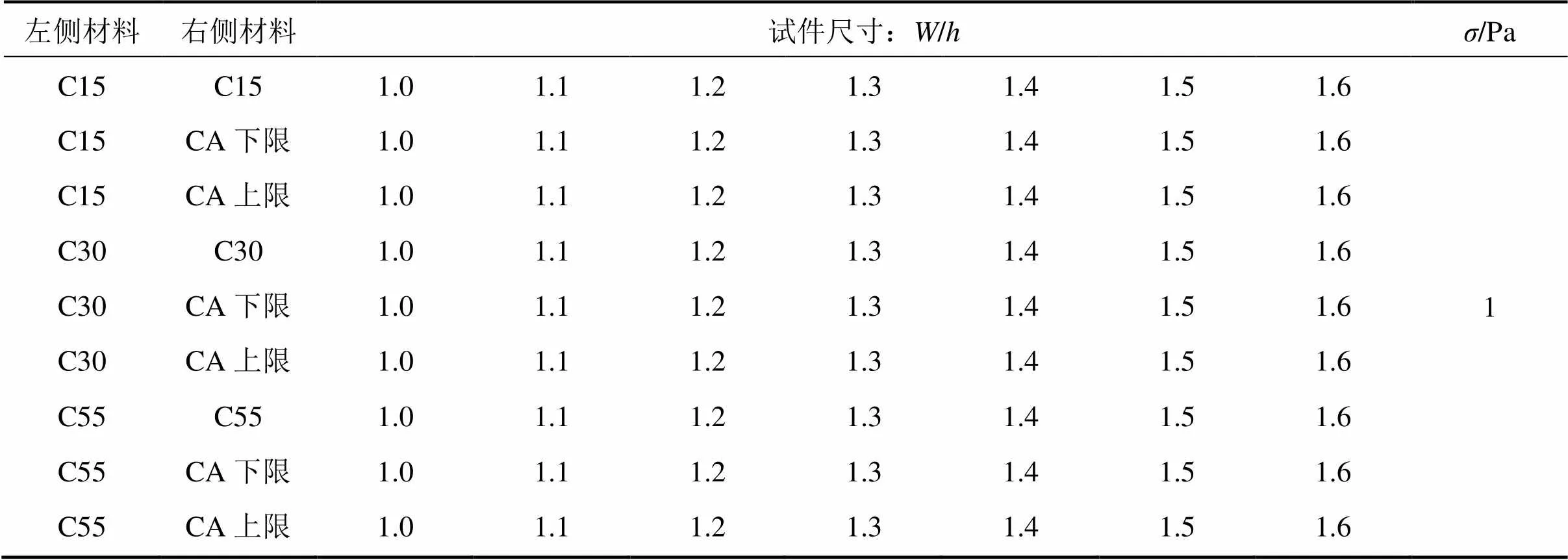
表2 计算工况

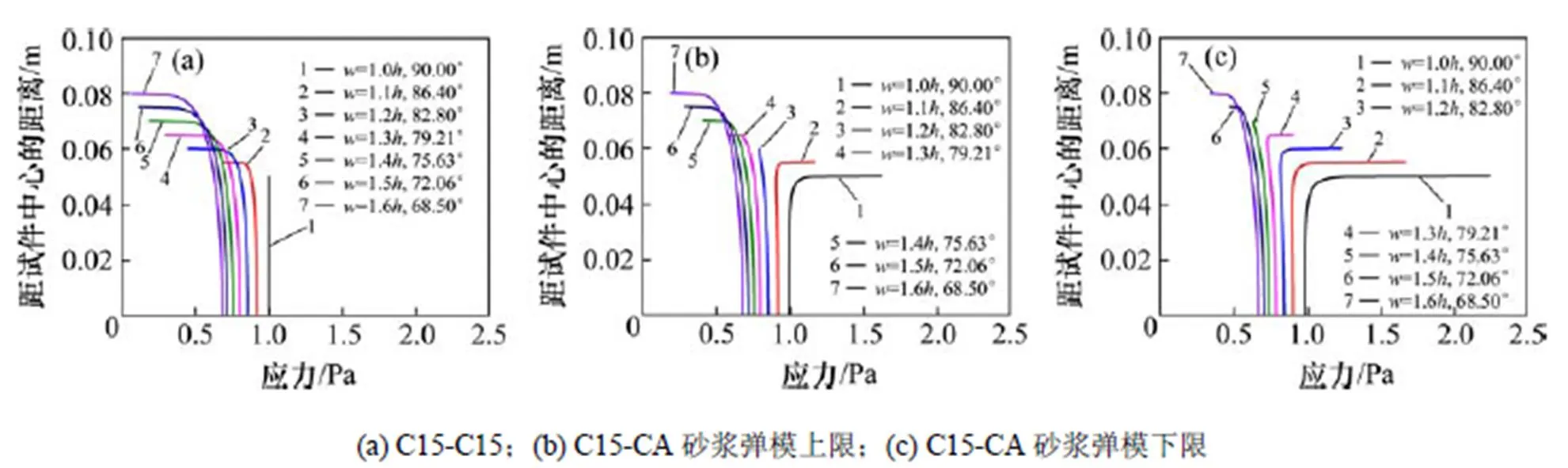
图9 试件尺寸对C15混凝土和CA砂浆界面应力分布的影响

由图9可知：对于C15-C15构成的单材料界面，界面端不存在应力奇异性；而对于C15-CA砂浆构成的双材料界面，当<1.5(1=2>72.06°)时，双材料界面端存在明显的应力奇异性，如图9(b)，9(c)所示，当≥1.5(1=2≤72.06°)时，双材料界面端的应力奇异性消失，此时应力场为一定值。这与图7依据Bogy特征方程计算结果是一致的，表明对于双材料界面，采取一定的角度组合是可以消除界面端的应力奇异现象。同理，其它工况的计算结果如图10~11所示。

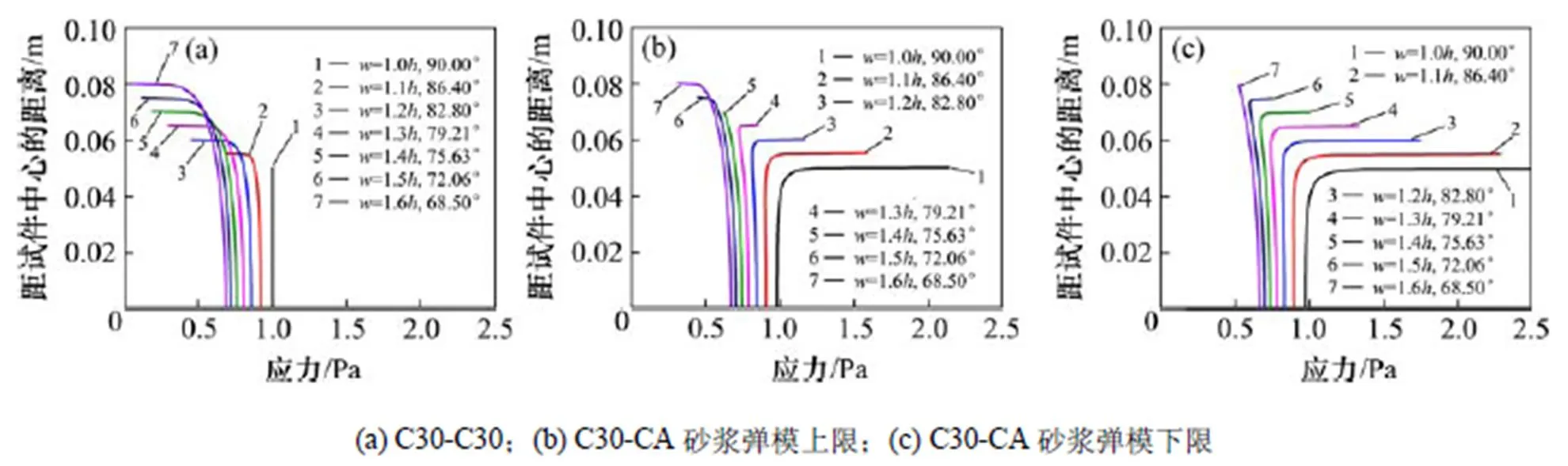
图10 试件尺寸对C30混凝土和CA砂浆界面应力分布的影响

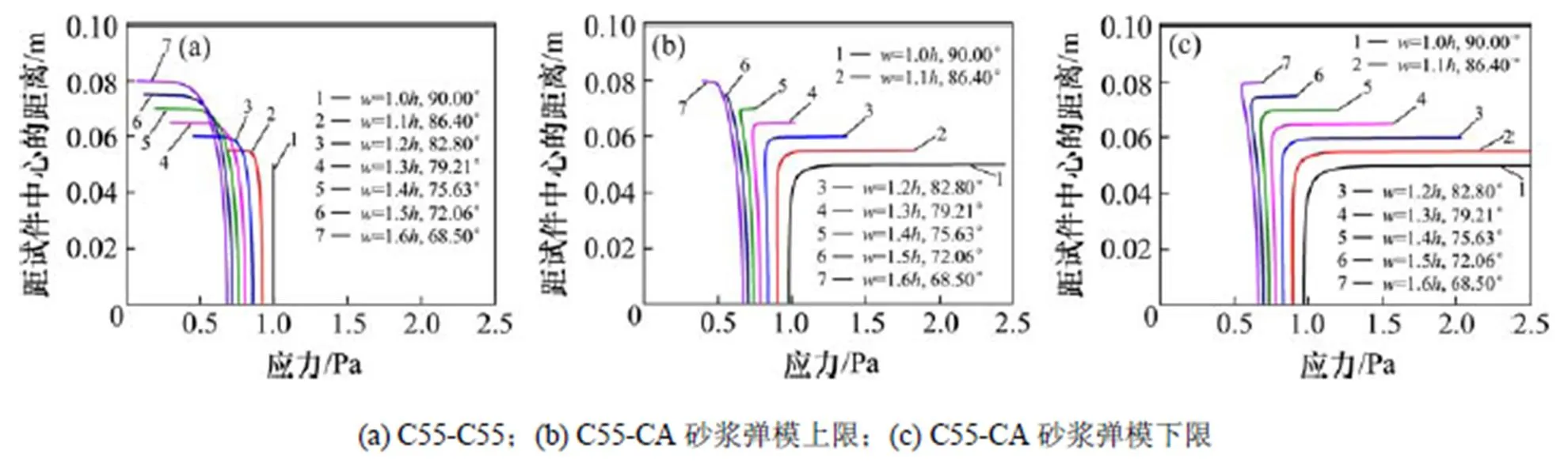
图11 试件尺寸对C55混凝土和CA砂浆界面应力分布的影响

4 试件界面中心应力场分布

通过改变结合角1和2的值，达到消除界面端应力奇异性的目的后，界面最大应力发生在界面中心处，此位置会成为界面发生破坏的首发区。通过对上述各工况进行计算，获得界面中心处应力与试件尺寸的关系如图12所示。

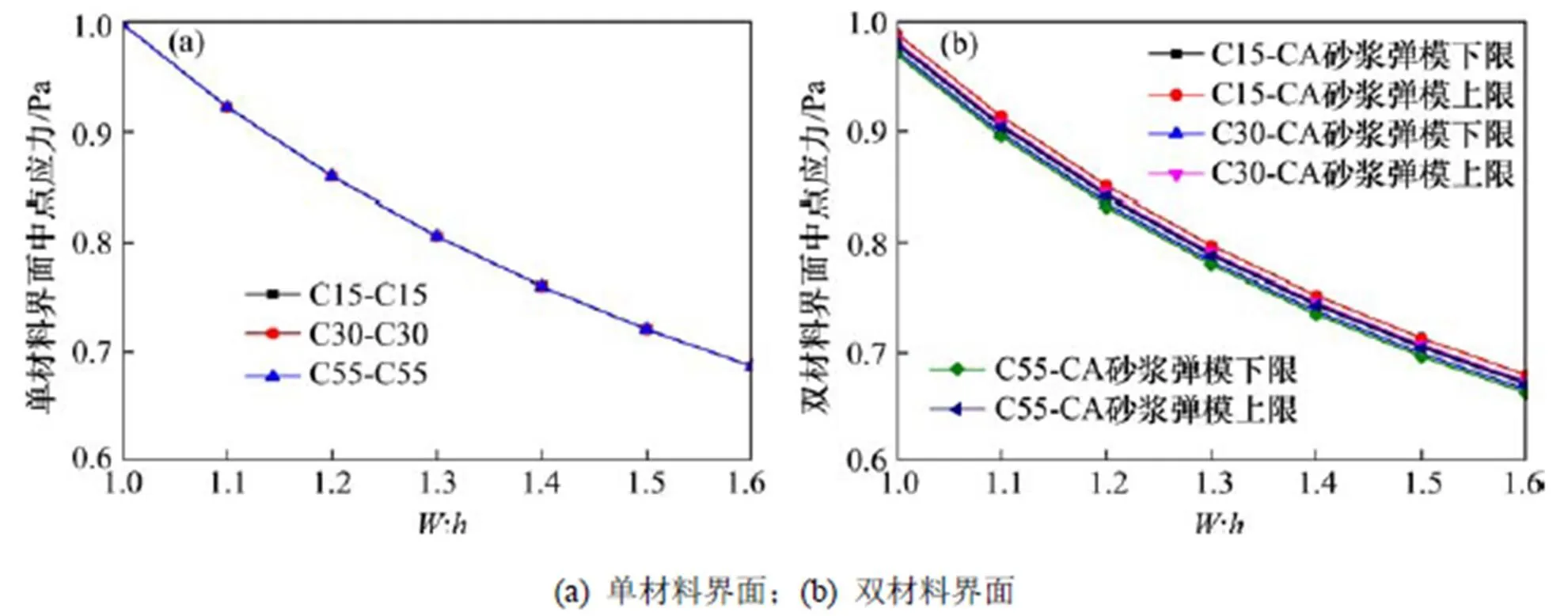
图12 试件尺寸对界面应力峰值的影响

由图12可知，界面应力随着试件尺寸的增加呈减小趋势。对于单材料界面，材料属性对界面应力并无影响；而对于双材料界面，由于两边材料性质不一致，在变形时为满足变形协调条件，会使得界面出现应力耦合效应，该耦合效应由界面端向中心逐渐减弱；图12(b)中不同的材料组合界面应力的差异性正是由于该耦合效应所致。而对于实际工程应用而言，该小于2%的微小差异基本可忽略不计。

对于=的试件，在轴向拉力的作用下，界面中心处拉应力与试件尺寸呈3次多项式关系，如式(3)所示：

式中：f为界面抗拉强度，Pa；为破坏荷载，N；为试件边缘半高度，m；为试件中间半高度，m；为试件形状系数；为试件厚度，m；为界面平均应力；max为界面最大应力；1，2，3和4为应力分布系数。对于不同材料组合的界面，该分布系数如表3所示。

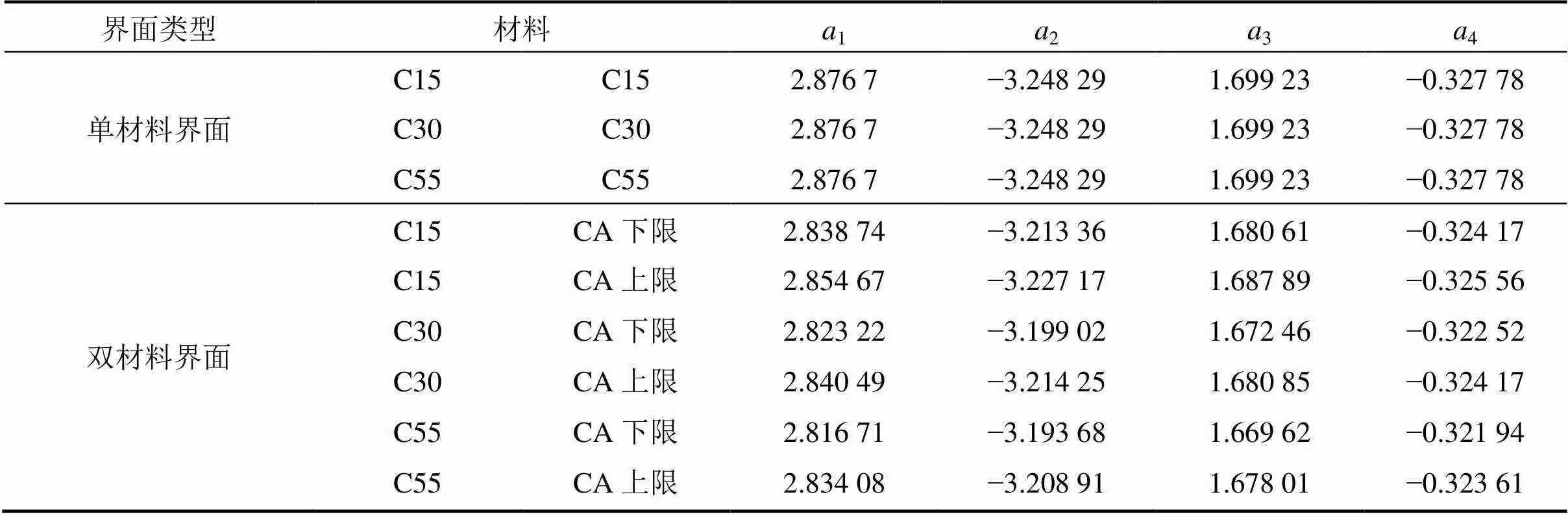
表3 不同材料界面对应的应力分布系数

5 双材料界面黏结强度试验设计

双材料界面黏结强度试验由拉力试验机、双材料复合试件及数据储存系统等构成，如图13所示。

1) 制作混凝土-CA砂浆复合型轴拉试件3组，共9个。按配合比要求拌制混凝土，取试件1/2长度所需要的混凝土量装入试模，放入养护室养护至要求的间隔试件后，按施工要求进行层面处理。按配合比要求拌制CA砂浆，装入剩下的1/2试模，并养护至试验要求龄期。

2) 到达试验龄期时，将试件从养护室取出，测量试件断面尺寸，精确到1 mm。

3) 试件安装在试验机上，开动试验机，进行2次预拉，预拉荷载约相当于破坏荷载的15%~20%。

4) 预拉完毕后，重新调整测量仪器，进行正式测试。拉伸时的荷载速度控制在0.4 MPa/min，每加500 N测读并记录变形值，直至试件破坏，并记录破坏荷载和断裂位置。

5) 将获取的破坏荷载极限值代入式(3)中，计算双材料界面的黏结抗拉强度。

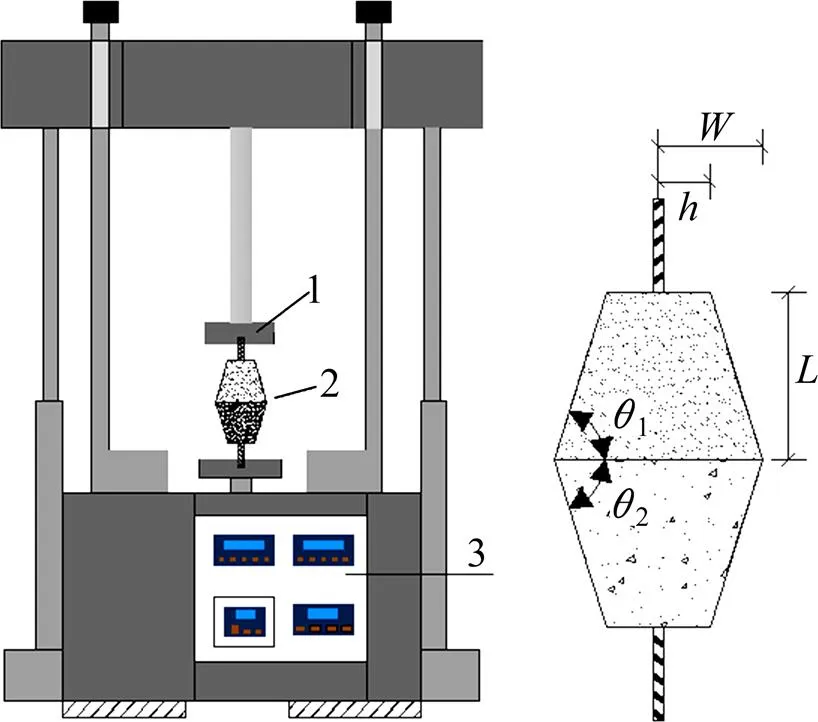
(1—加载头；2—混凝土-CA砂浆复合试件；3—控制面板)

6 结论

1) CRTSⅡ板式无砟轨道层间双材料界面端存在应力奇异性的现象，该应力奇异现象使得界面端点处的应力明显增加，可能是导致层间界面裂纹萌生和扩展的深层次原因。

2) 对于混凝土与CA砂浆组成的双材料界面端，当结合角组合1=2≤72°时，界面端的应力奇异性消失，此时应力场为一定值。

3) 根据消除双材料界面端应力奇异性的方法，设计出避开混凝土-CA砂浆双材料界面端奇异性的黏结强度试验方案。

[1] 姜浩. 双块式无砟轨道复合试件层间传力特性研究[D]. 成都: 西南交通大学, 2015. JIANG Hao. Research on transmission property of interlaminar structure[D]. Chengdu: Southwest Jiaotong University, 2015.

[2] 朱胜阳. 高速铁路无砟轨道结构伤损行为及其对动态性能的影响[D]. 成都: 西南交通大学,2015. ZHU Shengyang. Damage behavior of high-speed railway ballastless track and its effect on structure dynamic performance[D]. Chengdu: Southwest Jiaotong University, 2015.

[3] 刘柯, 戴公连, 朱乾坤. 简支铁路箱梁与轨道结构温度场仿真分析[J]. 铁道科学与工程学报, 2016, 13(4): 613−618. LIU Ke, DAI Gonglian, ZHU Qiankun. Simulation analysis of temperature field of simply-supported railway box girder and track structure[J]. Journal of Railway Science and Engineering, 2016, 13(4): 613−618.

[4] 元强, 郭建光, 邓德华, 等. 板式轨道用高弹模水泥沥青砂浆与混凝土黏结性能的试验研究[J]. 铁道科学与工程学报, 2013, 10(6): 40−44. YUAN Qiang, GUO Jianguang, DENG Dehua, et al. Experimental study on the bonding strength between high modulus cement emulsified asphalt for slab track and concrete[J]. Journal of Railway Science and Engineering, 2013, 10(6): 40−44.

[5] 张志超, 曾志平, 元强, 等. 温度荷载作用下桥上CRTS II型板式无砟轨道纵向力学特性研究[J]. 铁道科学与工程学报, 2015, 12(5): 982−989. ZHANG Zhichao, ZENG Zhiping, YUAN Qiang, et al. Study on longitudinal mechanical characteristics of CRTS II slab track on bridge under the temperature load[J]. Journal of Railway Science and Engineering, 2015, 12(5): 982−989.

[6] 戴公连, 粟淼. 剪切荷载下板式无砟轨道界面黏结破坏机理[J]. 华中科技大学学报(自然科学版), 2016, 44(1): 16−21. DAI Gonglian, SU Miao. Mechanism of interfacial bond failure for slab ballastless track under shear loading[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(1): 16−21.

[7] Bogy D B. Edge-bonded dissimilar orthogonal elastic wedges under normal and shear loading[J]. Journal of Applied Mechanics, 1968, 35(3): 460−466.

[8] Dundurs J. Discussion: “Edge-bonded dissimilar orthogonal elastic wedges under normal and shear loading”[J]. Journal of Applied Mechanics, 1969, 36(3): 650−652.

[9] Bogy D B. Two edge-bonded wedges of different materials and wedge angles under surface tractions[J]. Journal of Applied Mechanics, 1971, 38(2): 377−386.

[10] Kubo S, Ohji K. Geometrical conditions of no free-edge stress singularity in edge bonded elastic dissimilar wedges[J]. Transactions of the Japan Society of Mechanical Engineering, 1991(57): 632−638.

[11] 许金泉, 金烈候, 丁皓江. 双材料界面端附近的奇异应力场[J]. 上海力学, 1996, 17(2): 104−110. XU Jinquan, JIN Liehou, DING Haojiang. Singular stress field at interface edge of bonded dissimilar materials[J]. Shanghai Journal of Mechanics, 1996, 17(2): 104−110.

[12] 吴志学. 双材料界面端附近奇异应力场消除几何条件研究[J]. 工程力学, 2004, 21(6): 193−196. WU Zhixue. On the geometrical conditions of eliminating stress singularities near bi-material interface end[J]. Engineering Mechanics, 2004, 21(6): 193−196.

[13] SL 352—2006, 水工混凝土试验规程[S]. SL 352—2006, Hydraulic concrete test procedures[S].

[14] 李昌宁, 戴宇, 王亚国. CRTSⅡ型板式无砟轨道轨道板预制与铺设技术[M]. 北京: 中国铁道出版社, 2015. LI Changning, DAI Yu, WANG Yaguo. Prefabricate and laying technology of CRTSⅡ slab ballastless track[M]. Beijing: China Railway Press, 2015.

[15] OU Zumin, LI Fujian. Analysis and prediction of the temperature field based on insitu measured temperature for CRTS-II ballastless track[J]. Energy Procedia, 2014, 61: 1290−1293.

(编辑 涂鹏)

Research on eliminating the stress singularity at interfacial edge of concrete-CA mortar composite specimens

CAO Shihao, LI Jiali, KANG Weixin, LIU Xueyi

(MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China)

In order to study the stress singularity at interfacial edges of concrete and CA mortar, a model for calculating the axial tension of concrete-CA mortar bi-material composite specimen was established, and the tension stress distribution along the interface was analyzed. Based on the characteristic equation of Bogy, the method to eliminate the stress singularity at interfacial edges of concrete and CA mortar was presented. The results show that, there is a phenomenon of stress singularity at interfacial edges of concrete and CA mortar. The stress singularity at interfacial edges of concrete and CA mortar disappears when the bond angle satisfies1=2≤72°, and the stress field remains constant. The research findings presented could provide a theoretical basis for conducting the accurate tests for bonding strength of bonded dissimilar materials.

continuous slab track; interface edge of bonded dissimilar materials; stress singularity; characteristic equation of Bogy; bond angle

10.19713/j.cnki.43−1423/u.2018.09.007

U213.2+11

A

1672 − 7029(2018)09 − 2232 − 08

2017−07−26

国家自然科学基金重点资助项目(U1434208)

曹世豪(1988−)，男，河南焦作人，博士，从事轨道结构与轨道动力学研究；E−mail：531148108@qq.com