混凝土护栏在超高速磁悬浮列车碰撞下的有限元分析

毕继红，姜嘉琳，关健



混凝土护栏在超高速磁悬浮列车碰撞下的有限元分析

毕继红1, 2，姜嘉琳1, 2，关健1, 2

(1. 天津大学 建筑工程学院，天津 300350；2. 滨海土木工程结构与安全教育部重点实验室，天津 300350)

针对目前磁悬浮列车工程中，对护栏结构的研究稀缺，结合日本“东京——名古屋”段中央新干线磁悬浮列车的实际工程，针对磁悬浮列车护拦的防护作用，开展基于ANSYS/LSDYNA显示动力算法的仿真分析。模拟高速弯道过车时磁悬浮列车脱轨撞击护拦的过程。根据不同角度下列车撞击后护栏的变形结果，对护拦抵抗冲撞的能力进行对比分析。研究结果表明：在保证超高速运行的极限转弯半径下，磁悬浮列车脱轨撞击混凝土护栏，沿护拦擦撞形成沟壑状大面积损伤，但护拦未见穿透现象，仍能起到防护作用，阻止列车完全冲出轨道。对比相同速度下不同角度列车的撞击，极限转弯半径时，列车与护拦碰撞时的接触角度最大，此时护栏破损最为严重。

磁悬浮；护栏；失效单元；碰撞力

自20世纪60年代德国最开始研究磁悬浮交通以来，磁悬浮技术广受关注和青睐。与铁路和地铁系统相比，磁悬浮列车在100~1 600 km距离的交通方式上十分具有竞争性[1]。此外，磁悬浮系统的优点还包括脱轨风险更低，舒适性更强，低噪音和能量消耗较少[2−3]。20年来，针对磁悬浮系统展开了许多研究工作，包括车体的优化，磁悬浮系统的稳定性等等。为了分析不稳定机制，研究气隙控制性能，Kim等[4]提出了一种综合模型，结合3d车辆模型，灵活的导轨和带控制器的悬浮电磁体。为了获得地面震动的响应，WANG等[5]提出了一种三维多体车辆导向—土壤有限元模型，研究了高速磁悬浮列车在隧道中运行的地面振动。LI等[6]对30 m内的高速磁浮引起的环境振动进行了现场测量与系统分析。目前的大多数研究都针对车辆操作原理，车身动力学和转向架，导轨分析和设计，以及列车引起的地面震动等。磁悬浮列车的轨道侧壁的研究受到了忽视和制约。这是由于磁悬浮列车发展较晚，而线圈装于路轨上的“壁挂式”磁悬浮列车目前只在日本新干线上有实际应用，数量更为稀少，对于此种列车的研究几乎为0。而列车运行中断电，地震、路基沉降，异物干扰等均可能对列车安全行驶造成巨大影响[7]。防护栏是保障列车安全的最后一道屏障，因此应受到足够重视与研究。在实车试验成本极高，几乎不可能实现的情况下，计算机模拟为针对列车护栏的研究提供了一种经济可靠的思路。本文对防护栏的仿真模拟，可以更为直观的观察到突发情况下护拦的保护作用，并为今后的磁悬浮列车安全研究提供一定的基础性参考。

1 工程背景

在1999年日本开始着手研发高温超导磁体用于磁悬浮列车。2005年12月，在山梨县试验线路上的日本中央新干线磁悬浮列车运行速度达到553 km/h。在建中的新干线混凝土护拦的线路断面呈U字形，在侧壁内侧安装用于悬浮和导向的8字形线圈及用于牵引的直线电机线圈如图1，侧壁的具体参数详见几何模型介绍。本文研究的即兼具护栏和装置线圈功能的混凝土材料的磁浮轨道侧壁在列车突发脱轨事故后抵抗冲击的能力和对脱轨列车的防护与导向能力。

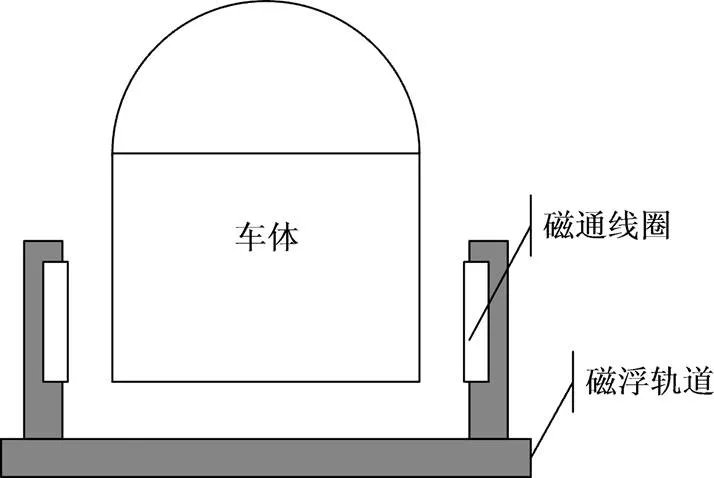
图1 护栏断面图

2 建立有限元模型

2.1 几何模型及网格划分

混凝土护栏的模型基于中央新干线的实际工程，所有相关数据均来源于工程。本文选取2段护栏进行分析。每段护栏长度为12.58 m，高1.525 m。建模时不考虑磁通线圈。护栏主体为混凝土材料，结构上分为上中下3部分，上下部分较厚，中间部分薄。上部厚度为0.35 m，中间部分厚度为0.231 m，底部厚度为0.81 m。在护栏底部由两排钢质螺栓支撑前排螺栓半径0.032 m，后排螺栓半径0.022 m，螺栓附近部分有高强混凝土灌浆加固，灌浆的宽度为0.7 m。2段护栏中间距离为0.02 m，由PC钢棒连接，PC钢棒半径0.023 m。螺栓及钢棒的材料参数见表1。在建立有限元模型的过程中，PC钢棒和螺栓采用空间梁单元beam161划分网格，混凝土采用三维实体solid164单元，螺栓、PC钢棒与混凝土单元通过共用节点的方式连接，简化的磁悬浮列车模型采用实体solid164单元。为保证计算结果的收敛及求解过程的高效，混凝土结构模型采用映射法划分网格。整个护栏的有限元模型如图2所示，全模型包含实体单元51 483个，梁单元97个，实体单元边长最小为 0.045 m。

图2 护栏有限元模型图

2.2 本构关系

2.2.1 螺栓及钢棒的材料模型

有限元模型中螺栓和钢棒采用MAT_ PLASTIC_KINEMATIC塑性随动模型。钢的材料参数如表1所示。

表1 钢的材料参数

2.2.2 混凝土材料模型

ANSYS/LS-DYNA广泛应用于碰撞和冲击荷载作用下结构响应的计算，提供了丰富的混凝土材料模型[8−9]。本文所采用的混土材料模型为第84号材料模型Mat_Winfrith_Concrete(MAT084)。此模型配合LS-DYNA的二次开发材料失效准则模型MAT_ADD_EROSION控制材料的失效。 Winfrith表达式比较复杂[10]，为了方便用户使用该模型，LS-DYNA要求用户输入混凝土的相关参数[11]来完成对模型的定义，混凝土需要设定的详细参数见表2。

表2 混凝土材料参数

2.2.3 接触算法

列车撞击护栏的接触算法通过*CONTACT_ ERODING_SINGLE_SURFACE定义，接触算法采用罚函数算法。同时为了防止出现沙漏现象，还加入了关键字Control_Energy和Hourglass。

2.3 边界条件

为简化计算，通过对护栏底部螺栓施加约束模拟护栏与地面的接触，约束螺栓底部节点的全部自由度。护拦上部及左右部分自由，不施加约束。

2.4 磁悬浮列车简化模型和初始条件

本文主要研究混凝土护栏在磁悬浮列车头车部分碰撞下的响应，磁悬浮列车碰撞时的变形不在研究范围内，因此磁悬浮列车头车部分将简化为一大质量的正方体实体，根据列车外部弧形形状，碰撞面积假设为0.01 m2，简化的磁悬浮列车头车部分质量取3.5 t。碰撞点选取左段护栏靠近PC钢棒处。列车初始速度为=152.8 m/s，与护栏相撞的角度为，=0.2°。

3 数值结果分析

碰撞角度为0.2°时磁悬浮列车与护栏碰撞后护栏状况如图3所示，为了显示更加清晰，还原失效单元并提亮。由于列车与护拦的碰撞角度较小，列车动量很大，列车与护拦碰撞后沿护拦进行擦撞运动，列车沿护栏擦撞时间为0.875 s，最终导致混凝土沿列车擦撞方向大量剥落，形成一道凹凸不平的沟痕，沟痕深度在擦撞过程中逐渐增大。护栏与列车直接接触部分混凝土单元全部破坏失效。而未直接与列车碰撞的护栏部分，混凝土单元部分失效，且失效单元数目随与擦撞部的远离逐渐减少。灌浆部位未见失效。

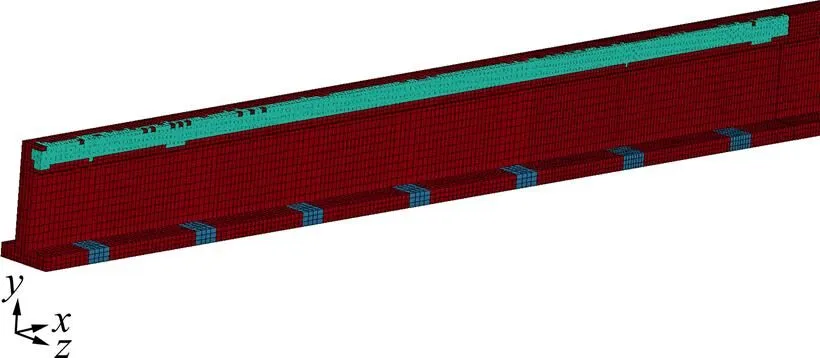
图3 还原失效单元后护栏破坏形态

图5为列车向速度时程，可以看出列车向位移有2个明显减小的时刻，第1个时刻出现在碰撞第一时刻0.005 s，第2个时刻出现在0.07 s左右。列车向碰撞力和碰撞力合力如图5，由于向碰撞力很小，碰撞力合力主要由和向碰撞力组成。由图6可以看出向碰撞力在碰撞第一时刻0.005 s时出现，骤然增至最大值，又很快减小至0，随后碰撞力偶有波动但峰值远远小于最大值，这说明在垂直护栏方向上，最危险时刻出现在碰撞第一时刻。此时混凝土承受碰撞过程中的最大垂向压力。同时可以看出波动出现在0.005 s和0.07 s，列车向碰撞力2个波动段对应着列车向速度变化最大的2个时刻。

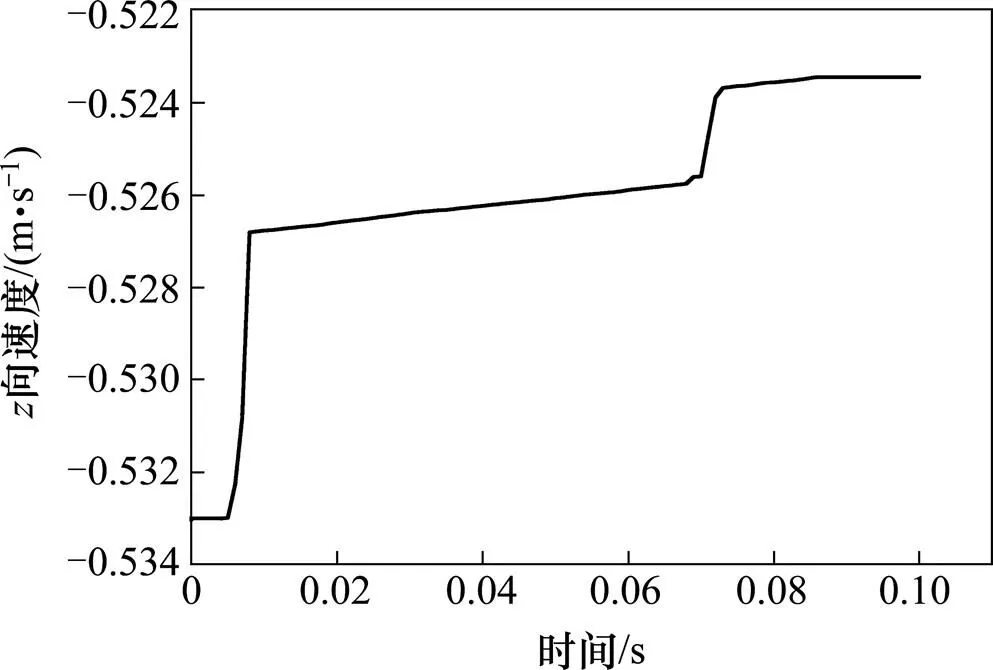
图4 列车z向速度时程图

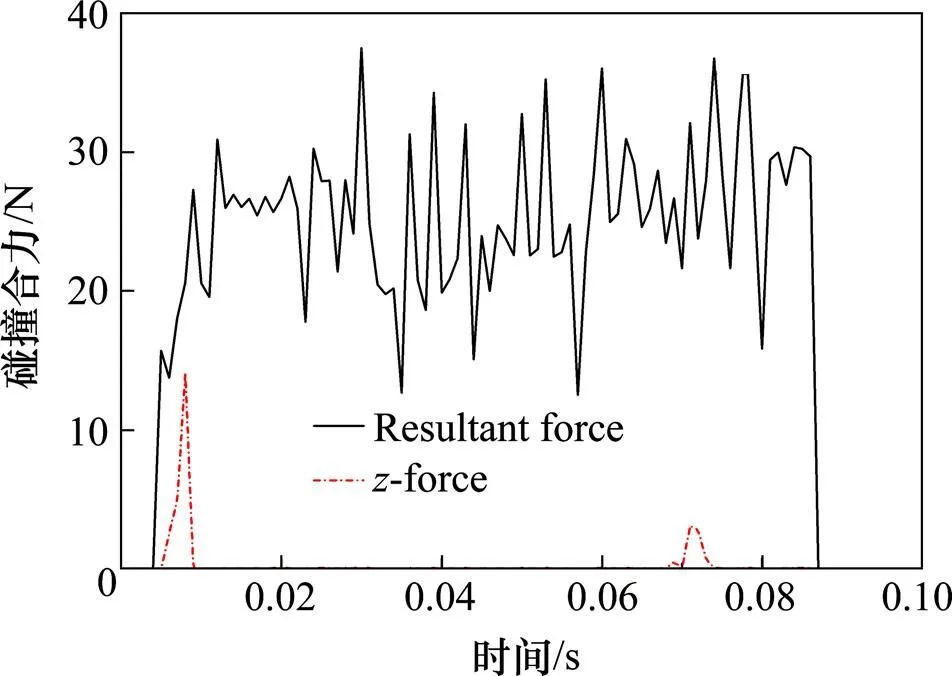
图5 碰撞力与碰撞合力时程图

在罚函数接触算法中界面接触力大小与穿透深度，主面的刚度成正比[12]。根据表4，可以看出碰撞力合力整体呈现波动趋势，直到列车离开护拦骤减为0，这是在碰撞过程中，撞深不断变化导致。

4 参数分析

改变初始条件中列车的初始碰撞角度，进行多角度碰撞分析并对比。找出了最不利的碰撞角度。并通过对最不利角度碰撞下的冲击响应分析，判断护栏的安全性和可靠性。

4.1 碰撞速度及角度的确定

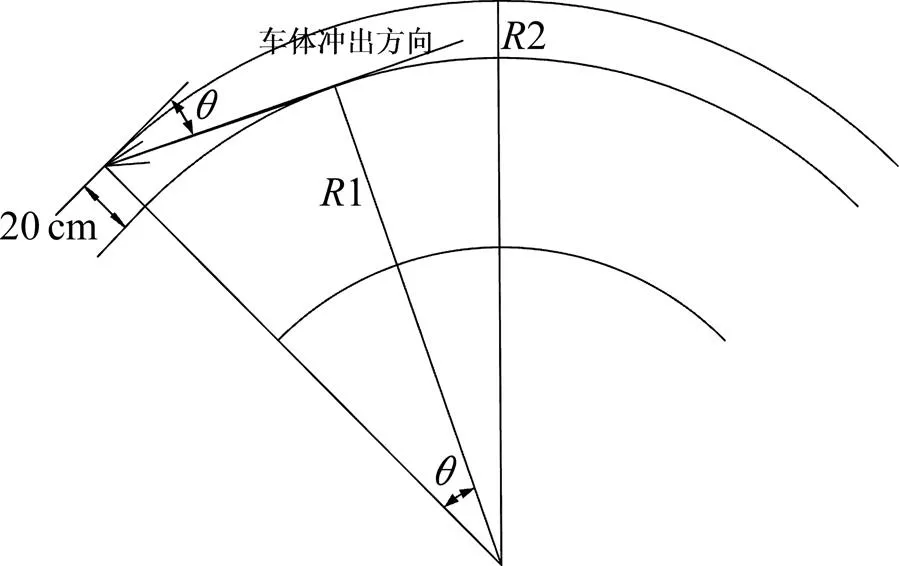
图6 碰撞角度示意图

4.2 不同碰撞角度下护栏对列车碰撞的响应

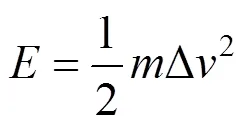
分析5种不同角度下的列车碰撞过程，总体来说碰撞过程过后，列车向和向速度减小量均变化较小，列车残余速度仍然很大。对比不同角度之间的向，向速度变化，可以看出随着增大，速度减小量也越大，列车碰撞前后能量变化量也相应增大。

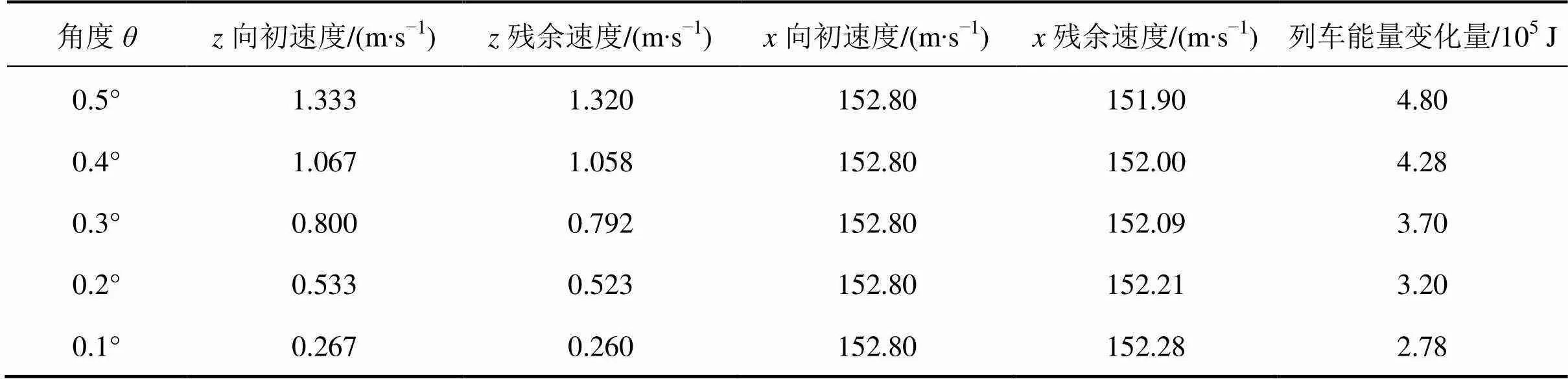
表3 不同角度下列车速度与能量变化

表4给出了破坏单元数，破坏单元占总单元数的百分比，最大侵蚀深度，碰撞合力最大值等的分析结果。作出破坏单元百分比与角度的关系图如图7，碰撞力合力最大值与角度的关系图如图8。

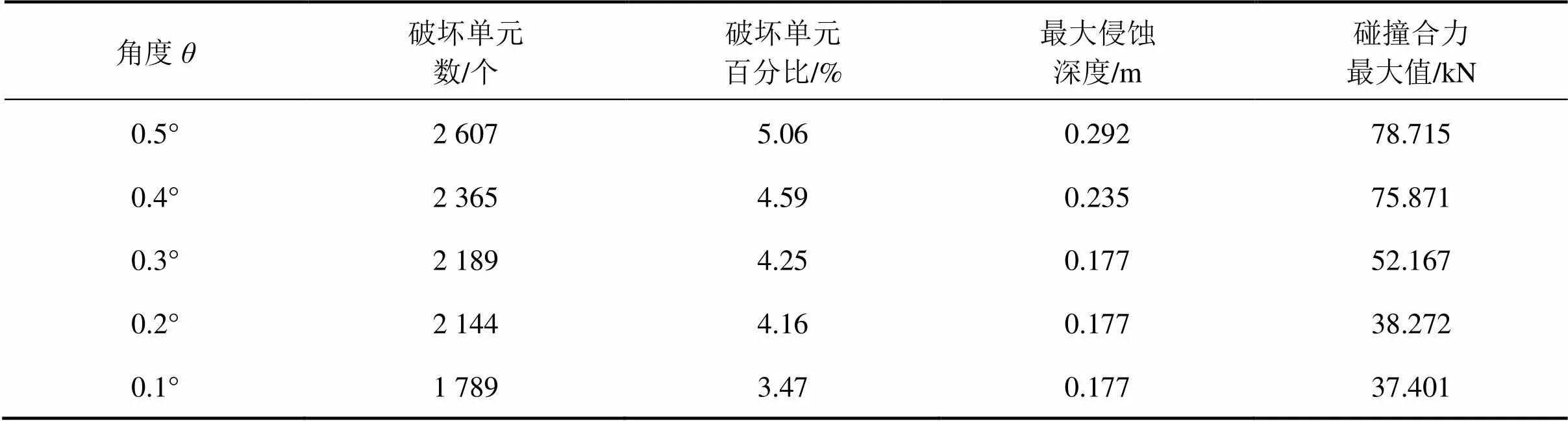
表4 不同角度下护栏破坏参数

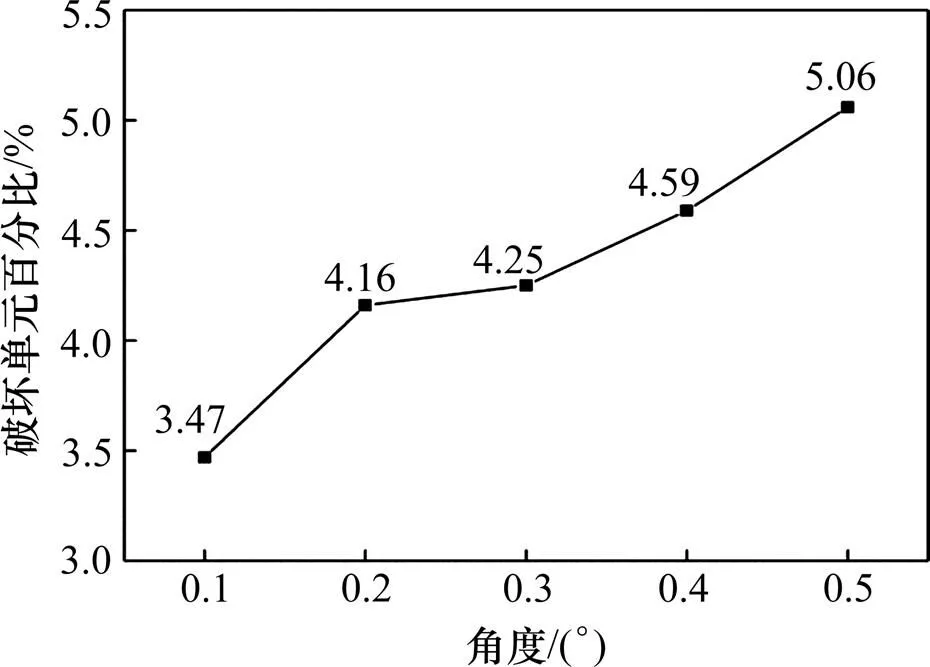
图7 破坏单元百分比与角度的关系

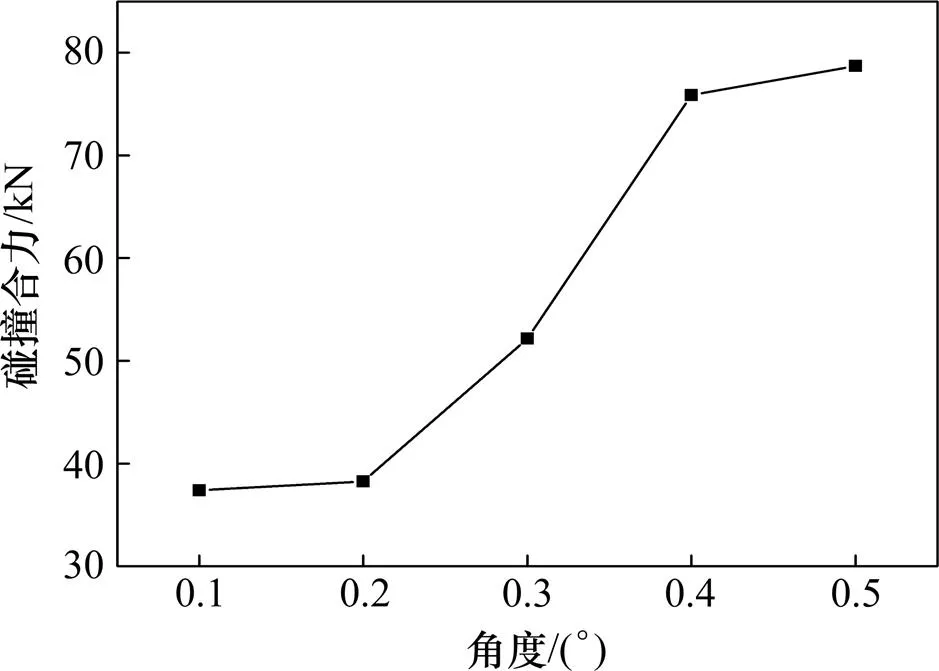
图8 碰撞力合力最大值与角度的关系

由表4可以看出，碰撞过程中失效单元占模型整体的百分比较小，只有3.47%~5.06%。由图8可以看出，0.2°~0.3°之间破坏单元百分比增量较为平缓。而角度0.1°~0.2°，0.3°~0.4°及0.4°~0.5°之间的破坏单元百分比增量较大。总体看来随着碰撞角度增大，破坏单元百分比随之增大，侵蚀深度呈明显增长趋势，这说明随着碰撞角度增大，护拦的破坏随之更为严重，且角度越大这种趋势越明显。由图8可以看出碰撞力合力最大值随碰撞角度的增大而增大，这说明角度越大对列车的影响也越不利。其中在极限角度0.5°时的碰撞对护拦的破坏最为严重，产生的碰撞力最大。

5 结论

1) 基于ANSYS/LSDYNA建立的有限元模型能较为真实的模拟列车擦撞并侵入混凝土护栏，最终导致护栏局部失效散裂的破坏效应。

2) 通过同一速度下列车以不同角度撞击护栏的对比分析可知，撞击角度越大，护栏的破坏程度越严重，其中以极限转弯半径下列车脱轨对护栏的影响最大。且随着角度增大碰撞过程中的碰撞力也越大，对列车的影响也更为不利。

3) 通过在最不利角度撞击护栏时的冲击响应分析，可以看出混凝土护栏基本能满足防护需求，在列车擦撞整个过程中未见大面积穿透破坏，护栏能在一定程度上起到导向和缓冲作用，能够防止列车冲出轨道彻底失控。

[1] Federal Administration. Final programmatic environm- ental impact statement maglev deployment program[R]. Washington, US, 2001.

[2] Lee H W, Kim K C, Ju L. Review of maglev train technologies[J]. IEEE Transactions on Magnetics, 2006.

[3] Yaghoubi H. The most important maglev applications[J]. Journal of Engineering, 2013(1): 9−19.

[4] Kim K J, Han J B, Han H S, et al. Coupled vibration analysis of maglev vehicle-guideway while standing still or moving at low speeds[J]. Veh Syst Dyn, 2015, 53(4): 587−601.

[5] WANG J, JIN X, CAO Y. High-speed maglev train- guideway-tunnel-soil modeling of ground vibration[C]// Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2011.

[6] LI G Q, WANG Z L, CHEN S, et al. Field measurements and analyses of environmental vibrations induced by high-speed maglev[J]. Science of the Total Environment, 2016.

[7] 屠旭永. 磁浮列车悬浮系统建模及悬浮控制策略的研究[D]. 杭州: 浙江大学, 2006. TU Xuyong, Research on modeling and control simulation & strategy for levitation system of maglev train[D]. Hangzhou: Zhejiang University, 2006.

[8] Hallquist J. LS-DYNA keyword user’s manual, version: 970[M]. Livermore: Livermore software Technology Corporation, 2007.

[9] WU Y, Crawford J, Magallanes J, et al. Performance of LS-DYNA® concrete constitutive models[C]// 12th International LS-DYNA® Users Conference, Issue 1, 2012.

[10] 顾佳伟. 撞击作用下PBX炸药响应过程的宏—细观数值模拟[D]. 北京: 北京理工大学, 2015. GU Jiawei. Macro and micro simulation of PBXs’ response under impact[D]. Beijing: Beijing Institute of Technology, 2015.

[11] Clark L A. CEB-FIP model code 1990[J]. Programs Usenix Unix Supplementary Documents, 2008.

[12] 郝好山, 胡仁喜, 康士廷. ANSYS12.0LS_DYNA非线性有限元分析从入门到精通[M]. 北京: 机械工业出版社, 2010. HAO Haoshan, HU Renxi, KANG Shiting. ANSYS12.0LS_DYNA nonlinear finite element analysis from entry to proficiency[M]. Beijing: Machinery Industry Press, 2010.

[13] 白雪. 高速超导磁悬浮列车的转向架设计[D]. 成都: 西南交通大学, 2011. BAI Xue, Design of the high temperature superconducting Maglev train bogie[D]. Chengdu: Southwest Jiaotong University, 2011.

(编辑 蒋学东)

Finite element modeling of concrete guardrail’s responses under impact of ultrahigh speed maglev train

BI Jihong1, 2, JIANG Jialin1, 2, GUAN Jian1, 2

(1. School of Civil Engineering, Tianjin University, Tianjin 300350, China; 2. Key Laboratory of Coastal Civil Engineering Structure and Safety, Ministry of Education, Tianjin 300350, China)

In the current maglev train project, the research on the guardrail structure is scarce, and the actual vehicle experiment is almost zero. Based on the engineering project of the Central Shinkansen maglev train in the “Tokyo-Nagoya” of Japan, this paper conducted the finite element analysis with ANSYS/LSDYNA explicit dynamic algorithm. The final deformation was obtained after simulation of the impact of the maglev train during turning in different angles. Comparing the protection ability of the guardrail in impacts, it shows that after the maglev train derails and collides with concrete guardrails at minimum turning radius, the guardrail forms large area damage, but penetration is not observed. The guardrail can prevent the train from completely out of the tracks. In comparison with situations at different angles in the same speed, when the train strikes the guardrail at the largest angle, the damage of guardrail is the most serious.

maglev; guardrail; failure element; impact force

10.19713/j.cnki.43−1423/u.2018.09.002

O347.3

A

1672 − 7029(2018)09 − 2196 − 06

2017−07−12

毕继红(1965−)，女，天津人，教授，从事复杂结构分析以及碰撞仿真分析研究；E−mail：jihongbi@163.com