基于三维扫描与数值技术的粗集料形状特征与级配研究

李良，龙广成，谢友均，曾晓辉，潘自立，东怀正

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中铁第二勘察设计院集团有限公司，四川 成都 610019；3.西藏铁路建设有限公司，西藏 拉萨 851400)

粗集料是工程中用量最多、最重要的建筑原材料[1]，构成了混凝土的基本骨架，占混凝土总体积的60%～80%。粗集料对混凝土拌合物硬化后的强度、收缩变形、耐久性和工作性能有重要影响[2]。因此，探索粗集料的几何形状特征、颗粒级配的科学、高效表征评价方法具有重要意义。粗集料形状特征包括颗粒组成、形貌特征、棱角性等。现有规范采用了颗粒级配、针片状含量等指标来评价粗集料的几何性质特征。一些研究者也采用了数学分析方法、二维数字化技术手段对粗集料颗粒级配、粒径大小和形状特征进行了研究[3-6]。总体上，粗集料颗粒构成及其形状特征的研究还存在不足，亟待加强现代数字化、信息化技术在粗集料颗粒组成、形状特征精细化测试方面的研究，继而优化粗集料级配及混凝土多元体系中的分布，最终改善混凝土工作性能、力学性能和耐久性。近年来，粗集料形状特征的研究得到广泛关注。李国强等[7-8]推导了从一维、二维到三维粗集料的级配分形维数、表面积分形维数和体积分形维数的计算公式。也有研究者开发相应的图像采集和分析系统，以及用数字图像技术实现粗集料二维图像分析处理，得到粗集料轮廓的形状特征[9]。MASAD 等[10]采用腐蚀-膨胀法来量化粗集料颗粒纹理。KOMBA 等[11]基于球谐变换法计算提出了粗集料的三维形状指标。BANGARU等[12]使用傅里叶级数拟合了粗集料图像轮廓，并提出评价粗集料形貌的指标。然而，这些研究方法都有一定的局限性，如粗集料的分形描述能够定性地描述粗集料在混凝土中的分布，但不能精确得到粗集料的形状参数；二维数值图像处理只能对粗集料的轮廓进行描述，无法得到三维的形状参数，且描述棱角性和纹理的指标受二维图像的像素影响较大，对粗集料的拍摄角度，拍摄环境要求较高，操作比较复杂。相比之下，三维扫描技术可以快速还原出粗集料的真实表面，得到更为精确、全面的粗集料几何形状参数，具有显著的优越性。鉴于此，本文结合三维扫描技术和数字化技术研究粗集料的级配和形状特征。基于分形几何学理论和MATLAB 程序计算得到粗集料的级配分形维数对粗集料级配进行分析，在此基础上提出粗集料的球度、长短轴长比和粒径离散度等指标评价粗集料的形状特征，继而结合级配分形维数计算得到粗集料的表面积分形维数描述粗集料表面粗糙程度，最终为实现粗集料几何形状性质的科学化、精准化和高效化表征评价提供技术支持。

1 粗集料形貌特征的数值描述

1.1 粗集料形貌的三维扫描与重构

利用HSCAN 型三维扫描仪扫描粗集料表面。三维扫描仪由2 个相机与激光器组成，分辨率有0.05 mm 和0.02 mm 可供选择。采集数据为粗集料表面各点的云坐标。三维扫描仪对粗集料表面进行扫描时，扫描平面上张贴标记点并放置需要扫描的粗集料。通过对每颗粗集料进行2次不同角度的扫描，用三维图形处理软件对2次扫描的公共面进行拼接，可实现粗集料三维结构的重建与表面三维坐标的获取。真实粗集料照片和重构粗集料图如图1所示。

图1 粗集料扫描处理及重构结果Fig.1 Results of coarse aggregate scanning and reconstruction

1.2 粗集料几何参数的获取

通过激光三维扫描技术可获得粗集料准确的几何尺寸参数如图2所示，包括长轴、中轴、短轴等。随机选取5～9.5 mm，9.5～16 mm 和16～20 mm 3 种尺寸范围粗集料各10 颗进行三维扫描，得到相应的轴长、面积、体积等参数，列于表1中(对各粒径范围粗集料仅列出3 颗的数据)。按式(1)可得粗集料表面积系数Ks与体积系数Kv比：

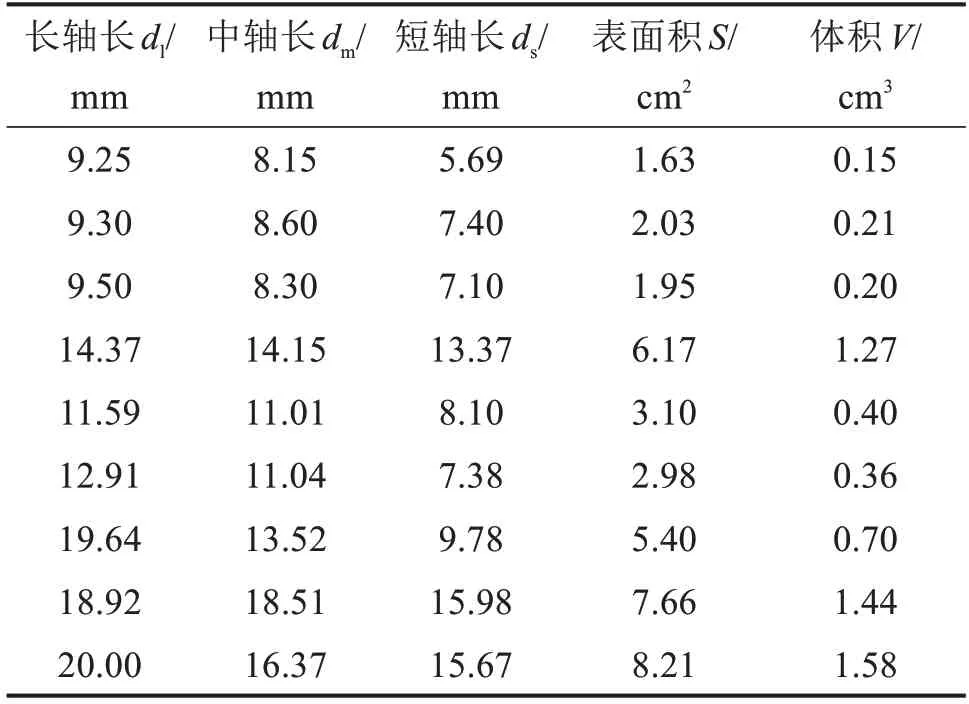
表1 粗集料表观尺度参数扫描计算结果Table 1 Calculation results of aggregate apparent scale parameters scanning

式中：x为粗集料的粒径，统一为粗集料的最大尺寸(长轴长)；S为粗集料的表面积；V为粗集料的体积。

1.3 粗集料形状的数值综合表征

1.3.1 外形特征评价参数

粗集料的形状多不规则，考虑实际粗集料的三维形状特征，结合三维图像技术，将粗集料在x，y和z3 个方向上的长度从大到小定义为长、中和短轴长(如图2)，采用球度参数来描述粗集料的不规则程度，由式(2)能够计算粗集料的球度Ψ[13]，解决了二维数字图像和传统测量粗集料形状特征参数不准确的问题[14]。

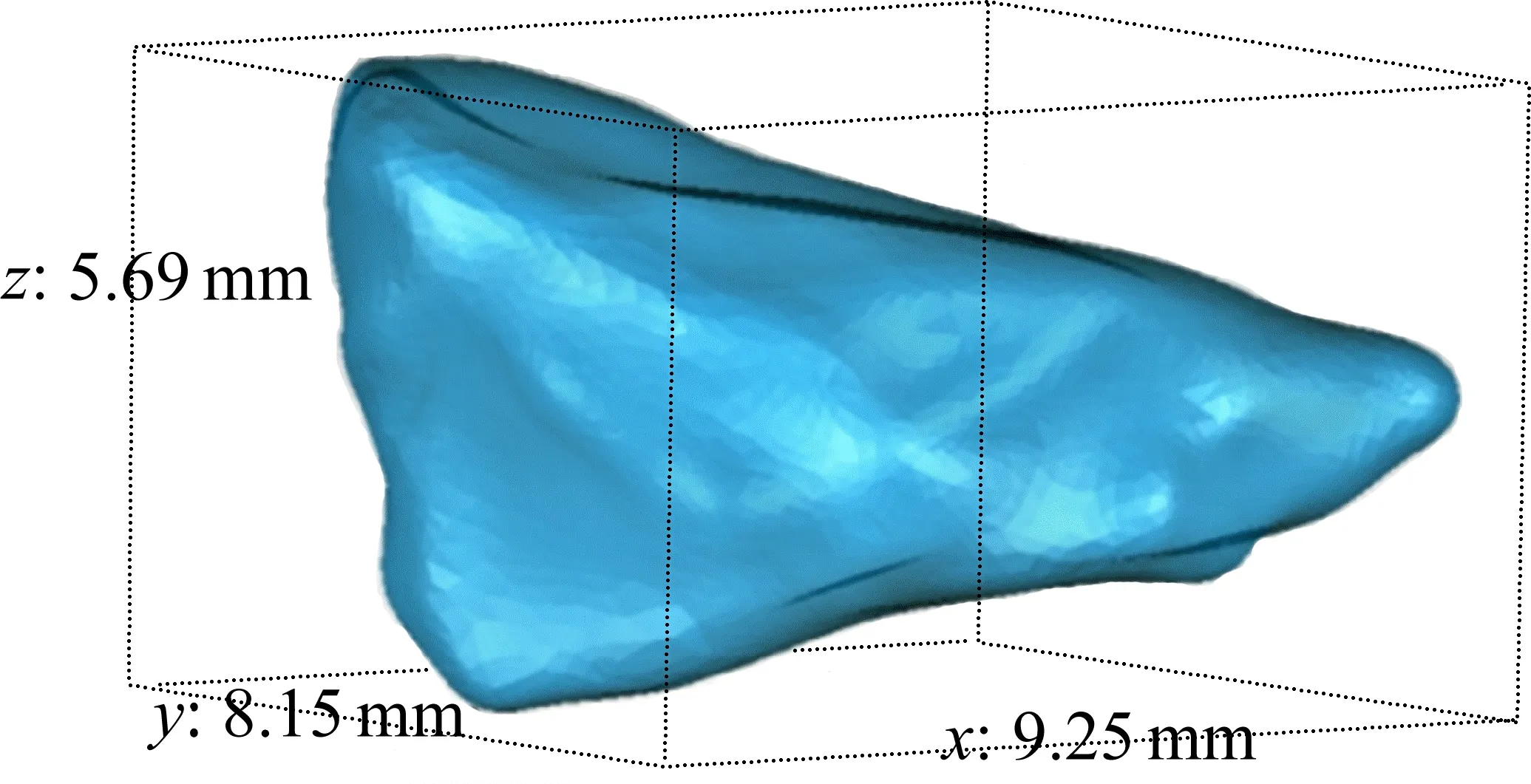
图2 粗集料三维形状几何尺寸计算结果Fig.2 Calculation results of three dimensional shape and geometric dimension of aggregate

根据得到的长轴长dl和短轴长ds，定义长短轴长比来描述粗集料针片状特征，由式(3)能够算得粗集料的长短轴长之比α；假定粗集料的形状为理想球形，则在任意方向上(包括x，y和z3个基本方向)的粒径尺寸都相同。根据粗集料实际在x，y和z3 个方向的不同粒径尺寸，定义粗集料3 个方向的最大尺寸与3 个尺寸均值的比值为粒径离散度，用粒径离散度λ来描述粗集料的不规则程度，由式(4)可以算得。

式中：Ψ，α，λ分别为粗集料的球度、长短轴长比和粒径离散度；dl，dm，ds分别为粗集料的长轴、中轴和短轴长。

1.3.2 不同粒径粗集料的形状特征评价

以下采用上述定义的球度、长短轴长比和粒径离散度3个形状特征参数，来描述评价粗集料的外形特征。基于扫描得到的30 颗粗集料的形状参数，可计算得到每一颗粗集料的3 个形状特征参数，并分析其与各自粗集料粒径之间的关系，以粗集料的最大线度尺寸(长轴长dl)作为粗集料的粒径，分析粗集料球度、长短轴长比和粒径离散度与粗集料粒径之间的关系，结果如图3所示。

粗集料的球度值在0～1 之间，且球度值越接近1，粗集料形状越规则[13]。如图3，这批试验粗集料球度良好，球度值为0.7～0.9，均值为0.88；离散度值均大于1，有少数接近1，最大可达1.3；值得注意的是，粒径离散度与球度基本呈现关于y=1函数的对称分布，粗集料球度越接近1，其粒径离散度也越接近1，粗集料形状越规则；另外，可以发现粗集料的长短轴长比值大于其离散度指标，且长短轴长比值与粒径离散度的分布大体相同，粗集料的长短轴长比值越大，粒径离散度也越大，粗集料的形状越不规则。

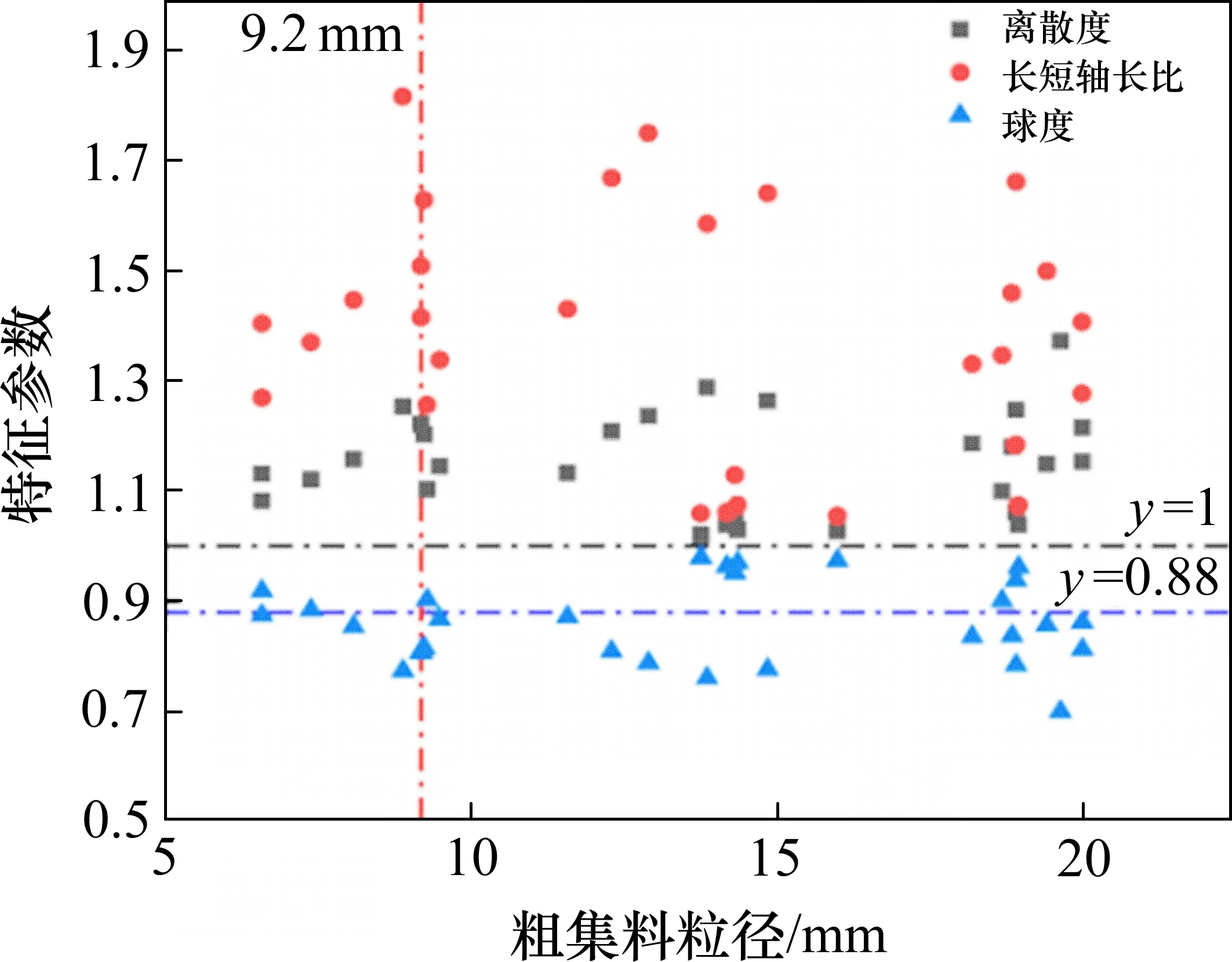
图3 粗集料形状特征参数与粒径关系计算结果Fig.3 Calculation results of the relationship between aggregate shape characteristic parameters and particle size

总体而言，所调查3种粒径粗集料的形状特征与粒径相关性不显著；所提出的粗集料球度、长短轴长比和粒径离散度3个参数之间具有较好的相关性和联系，基本能对粗集料外形特征进行描述，而对于粗集料球形度(三维尺度的一致度)描述，长短轴长比指标更具显著性和敏感性。

1.4 粗集料分形特征

1.4.1 颗粒级配分形维数

李国强等[7]提出的粗集料级配分形维数的计算是通过粗集料的筛选通过率来得到的，在进行粗集料三维扫描时发现，粗集料筛分无法全面准确获取其三维尺寸，粗集料形状的不规则性导致粗集料三维方向上的尺寸不尽相同，采用对应孔径的筛子对粗集料进行筛分时，任一方向尺寸小于筛子孔径，其他方向尺寸却大于筛子孔径的粗集料也可进入下一个级配。所以在筛分粗集料的过程中，粗集料的粒径区分不够准确，进而导致粗集料级配分形维数的计算误差。本文基于盒子计数法对粗集料表面点云坐标进行数值计算，可更准确地得出粗集料级配分形维数。

盒子计数法[15]将一个三维表面划分为多个立方体单元，每个立方体单元视为一个盒子，三维表面各点的不同高度视为盒子的高度。用各个高度不同的盒子对三维表面进行覆盖，最后统计完全覆盖表面的盒子数目与定义的立方体盒子的尺寸。按照分形的定义，盒子数与盒子尺寸分别取对数之后的函数斜率，即为分形维数，可通过MAT‐LAB程序计算得到，具体计算步骤如下：

1) 导入粗集料三维点云坐标进行分析，寻找空间中相邻的4 个均不为0 的数据点，定义为数组a，即将粗集料表面离散出的点云坐标，微分任意4 个点构成的平面用盒子进行覆盖，按数组a中的数据，根据相应的分形尺寸来计算需要的分形盒子数。

2) 对分形盒子数和分形尺度分别取对数，画出对应的散点图并进行多项式拟合，得到多项式(直线)斜率，即分形维数值。

3) 将每颗粗集料的点云坐标数据导入到写好的MATLAB程序中，即可进行计算。以5～9.5 mm的其中一颗粗集料为例，得到粗集料分形维数坐标图，分形维数坐标图中直线斜率即为粗集料级配分形维数，算得斜率值为2.845 3(一般粗集料的级配分形维数值在2～3 之间[7])，计算结果如图4所示。

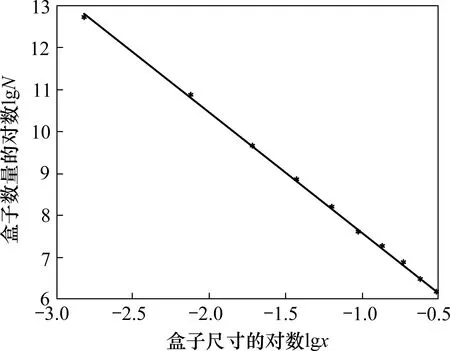
图4 某粒径粗集料的级配分形坐标及结果Fig.4 Fractal coordinate and result diagram of a gradation of a certain particle size aggregate

图5进一步给出了不同粒径(5～20 mm)30颗粗集料的级配分形维数变化结果。

图5 粗集料级配分形维数对粒径的变化关系结果Fig.5 Results of relationship between fractal dimension of aggregate particle size and particle size

从图5可以发现，对应粒径区间的粗集料级配分形维数随着粒径(粗集料长轴长dl)的增大而减小。若以所有调查粗集料的级配分形维数的质量加权平均值来作为5～20 mm 连续级配下粗集料的级配分形维数，可算得连续级配粗集料的级配分形维数Dc=2.768。

1.4.2 颗粒表面积分形维数

从一维的级配粒径分形到二维的表面积分形，可根据式(5)来计算得到粗集料颗粒表面积分形维数[8]。传统的测量方式和二维图像处理技术都无法准确得到单个粗集料的表面积和体积，进而无法准确得出粗集料的表面积分形维数。陈开端[16]通过测定粗集料的吸水量来测量粗集料的表面积，采用10 颗粗集料表面积的平均值来消除误差。但这种方法效率较低。利用三维扫描技术实现了单个粗集料表面积和体积的快速测量，可按照式(5)准确算得各粗集料的表面分形维数Ds。

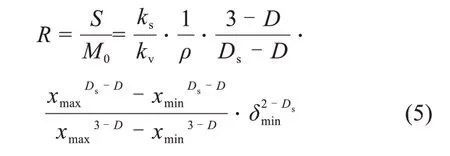
式中：R为粗集料的比表面积；S为粗集料表面积；M0为粗集料的质量；ks/kv为粗集料体积系数与表面积系数比；xmax，xmin分别取粗集料的最大和最小线度尺寸dl，ds(长轴长、短轴长)；D为所求粗集料的级配分形维数；δmin为分形盒子的最小尺寸，在MATLAB中取0.06 mm。

图6给出了不同粒径粗集料的表面积分形维数计算结果。从图中结果可以看出，在不同的级配粒径范围内，粗集料表面积分形维数对粒径的变化趋势相同，都随着粗集料粒径的增大而减小；对比图5 和图6 可以发现，粗集料的级配分形维数和表面积分形维数，在相应级配范围内，都随着粒径的增大而减小；不同的是，相对于表面积分形维数，级配分形维数与粗集料粒径的相关性更强，整体随粒径的增大呈下降趋势。

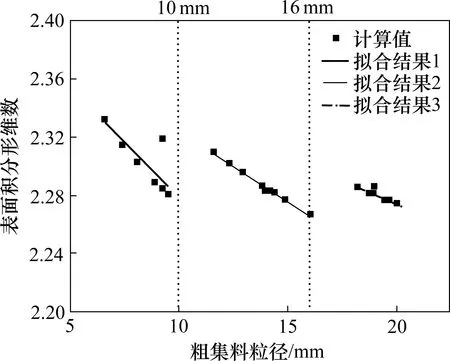
图6 粗集料表面积分形维数对粒径的变化关系结果Fig.6 Relationship between aggregate surface integral dimension and particle size change results

1.4.3 粗集料表面粗糙度

基于三维扫描得到的粗集料表面积和体积参数，可以描述粗集料表面的粗糙程度。粗集料表面越粗糙，在增大粗集料表面积的同时，并不会造成粗集料体积的大幅度增加。通过式(6)计算得到粗糙度指标(即粗集料真实表面积与体积的比值μ)，来对粗集料的粗糙程度进行评价。粗集料越粗糙，单位体积的粗集料表面积越大。

式中：S为粗集料表面积；V为粗集料体积。

图7 为不同粒径粗集料的表面粗糙度计算结果，图8进一步给出了粗集料表面积分形维数与粗集料粗糙度之间的关系结果。

图7结果显示，随着粗集料粒径的增大，粗集料表面粗糙度呈现明显降低。从图8 中可以发现，粗集料的表面分形维数随着粗集料粗糙度的增大而呈现增加趋势，两者具有较好的相关关系。这可从2个参数的涵义得到解释，粗集料的表面积是符合分形特征的，由式(5)可以得出，粗集料表面积分形维数随比表面积的增大呈现非线性增加[8]；由式(6)推导出粗集料粗糙度与比表面积的换算公式(7)可知，粗集料粗糙度同样随比表面积的增大而增大。由此可知，粗集料的表面积分形维数与粗糙度之间具有较好的相关性。

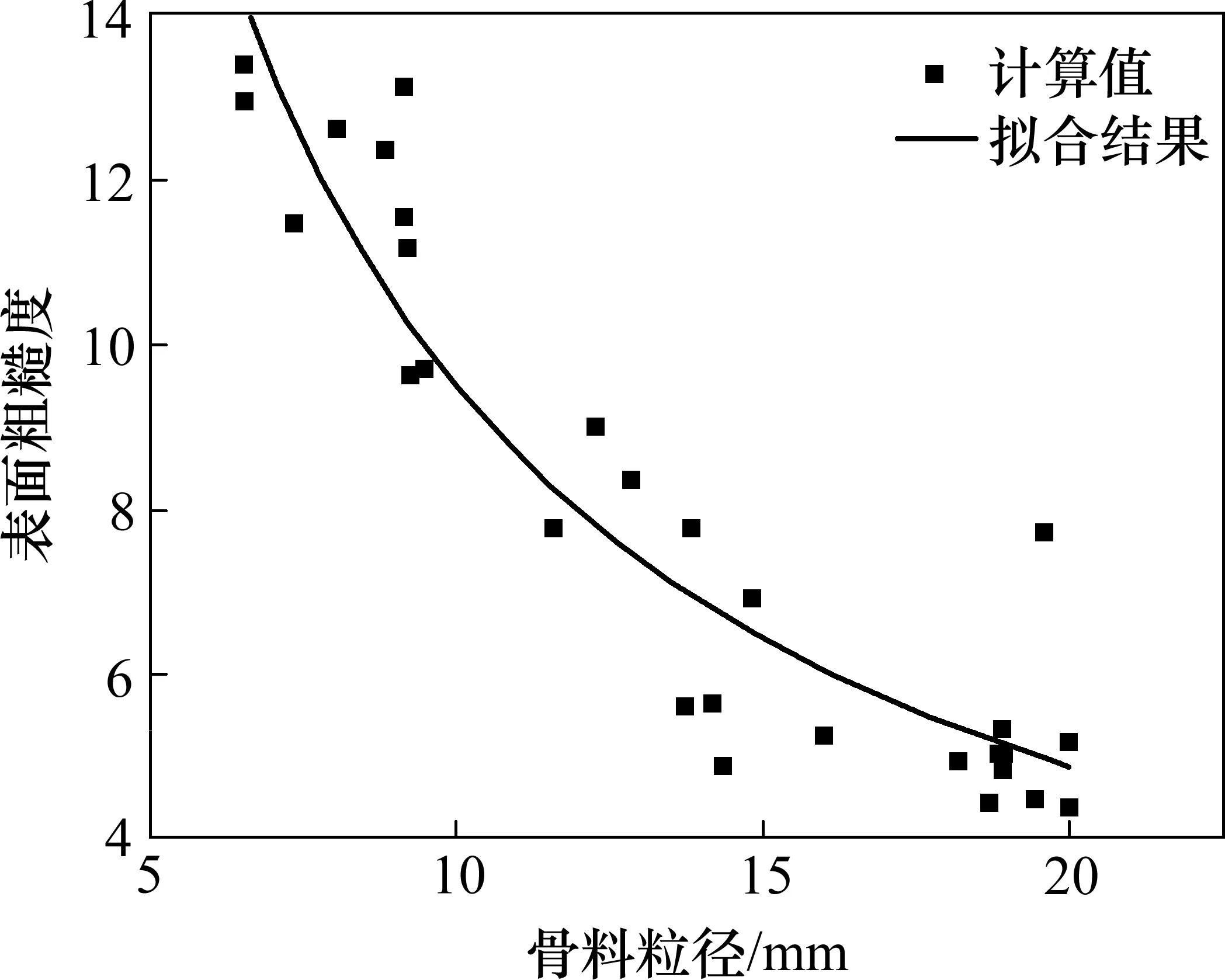
图7 不同粒径粗集料的表面粗糙度随粗集料粒径的变化结果Fig.7 Surface coarseness of aggregates with different particle sizes varies with aggregate particle sizes

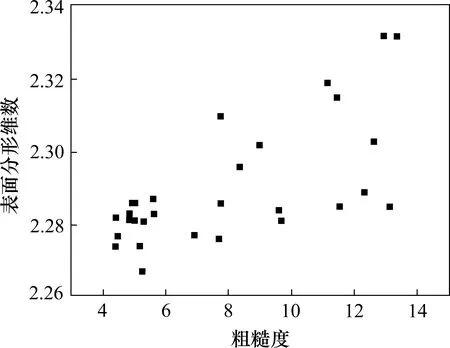
图8 粗集料表面积分形维数与粗糙度的变化关系结果Fig.8 Relationship between aggregate surface integral dimension and roughness

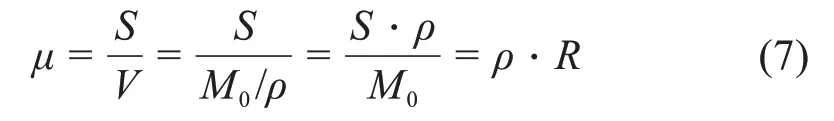
式中：M0为粗集料质量；S为粗集料表面积；ρ为粗集料密度；R为粗集料比表面积。

2 基于级配分形维数的粗集料级配分析

2.1 粗集料颗粒级配与分形维数的关系

从上述得到的粗集料级配分形维数结果可发现，在不同粒径区间内，粗集料的级配分形维数呈现出随粗集料最大粒径增加而减小的变化规律，这表明粗集料级配与其级配分形维数之间存在密切联系。基于颗粒体系最紧密堆积原理以及FULLER 等[17-18]提出的颗粒级配计算模型，并结合李国强等[7]的研究结果，可推导得到粗集料级配分形公式，如式(8)所示。

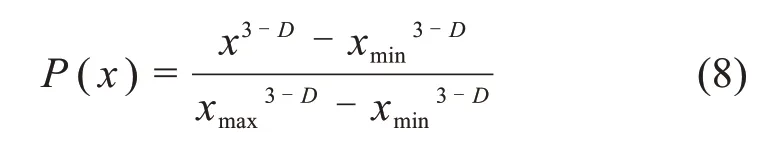
式中：P(x)为最大粒径为x的粗集料通过率；D为连续级配粗集料的平均级配分形维数Dc；x为粗集料的最大线性尺寸(长轴长dl)；xmax，xmin分别为连续级配区间的最大、最小粒径。

式(8)中指数“3-D”是分布模量参数，这个参数对于粗集料级配的合理性非常重要，参数的取值不同，所得结果也不同，这取决于分数维数D的合理计算获取，分形维数D代表粗集料系统颗粒粒径分布特征参数。本文采用上述按质量加权得到连续级配粗集料的级配分形维数作为公式中的D。根据前述得到的5～20 mm 连续级配粗集料的级配分形维数Dc(2.768)，代入式(8)中，可得到粒级范围级配通过率函数如式(9)所示：

2.2 试验验证

采用筛分试验对粗集料级配与级配分形维数关系的合理性进行了验证。基于现行规范选择5～20 mm 连续粒级的碎石粗集料5 kg，通过筛分试验得到各粒级的通过率，如表2所示。

表2 试验选取的5～20 mm粗集料筛分粒级分布结果Table 2 Grain-size distribution results of 5～20 mm aggregate screen selected in the test

由图9中的结果可知，式(9)计算得到的级配通过率曲线与筛分试验测试值两者具有高度的一致性。这表明可由式(9)计算得到合理的颗粒级配组成。因此，可利用激光三维扫描和数值分析技术，精确得到粗集料级配分形维数，从而实现粗集料级配的表征。

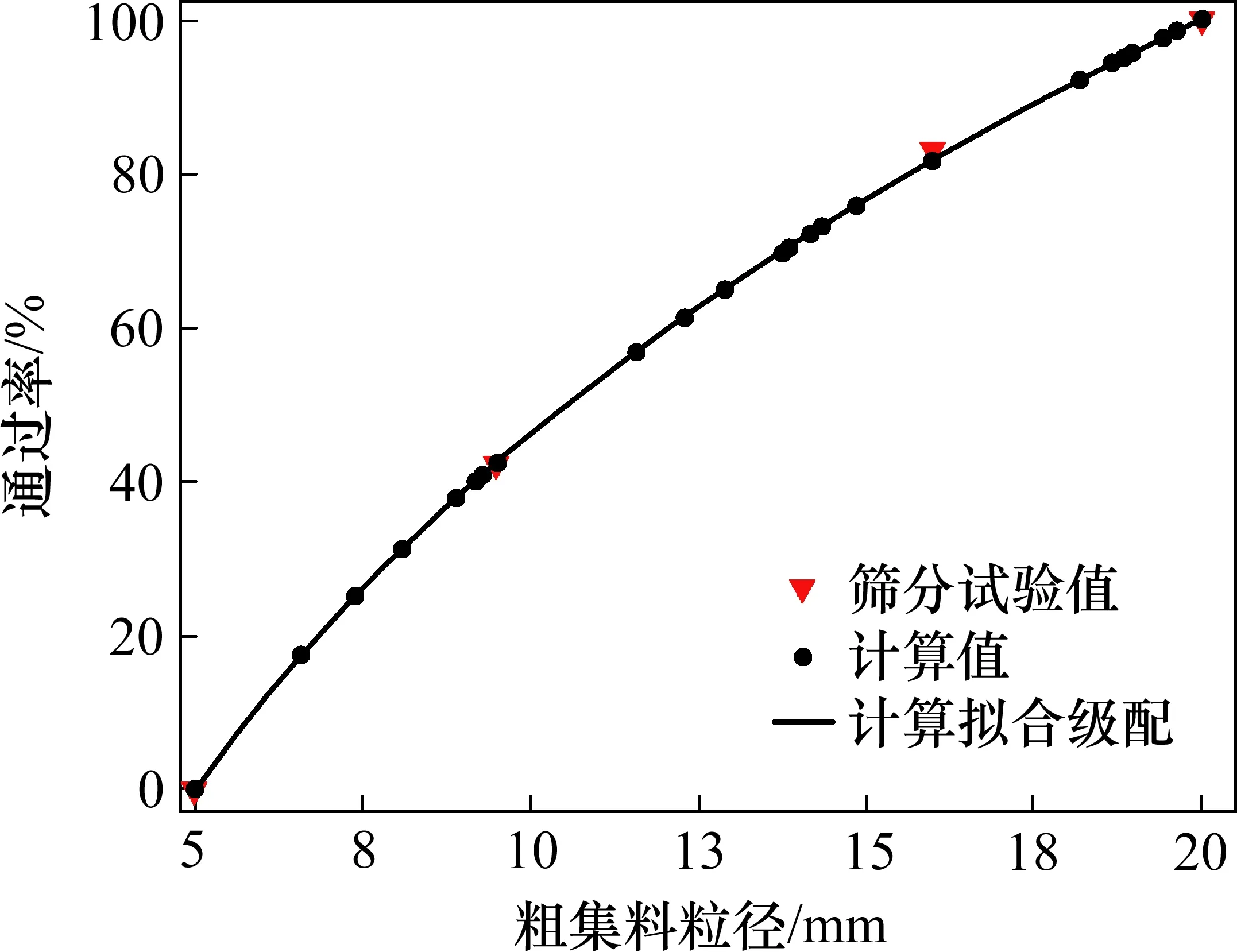
图9 粗集料级配的数值分析结果和筛分试验结果对比图Fig.9 Comparison of numerical analysis results and screening test results of aggregate gradation

3 结论

1) 激光三维扫描和数值分析技术可快速重构出粗集料的真实形状并准确测量出三维形状参数，实现了粗集料形状更准确表征。

2) 根据三维扫描技术得到的粗集料三维形状参数，提出了球度、长短轴长之比和粒径离散度3个指标，均可较好地对粗集料形状特征进行表征评价。其中，长短轴长之比指标表征评价粗集料形状特征更具显著性和敏感性。

3) 采用数值技术进一步处理三维扫描测试结果，可快速得到粗集料的级配分形维数、表面积分形维数以及表面粗糙度指标，实现了粗集料几何特征的数值描述和评价。粗集料级配分形维数、表面分形维数均随着颗粒粒径不同而变化，且表面分形维数与表面粗糙度之间存在密切联系。

4)采用质量加权得到的粗集料级配分形维数，建立了粗集料颗粒级配通过率计算函数，计算结果与试验结果一致，为粗集料颗粒级配分析的数字化、高效化提供了技术支持。