ZPW-2000轨道电路的多轮对动态分路建模研究

傅佳伟，王小敏，郭进

ZPW-2000轨道电路的多轮对动态分路建模研究

傅佳伟，王小敏，郭进

(西南交通大学 信息科学与技术学院，交通信息工程及控制重点实验室，四川 成都 611756)

针对现有ZPW-2000轨道电路单轮对分路模型难以反映列车真实分路情况的问题，提出一种轨道电路多轮对动态分路建模方法。根据实际列车分路情况下轮对与补偿电容和轨道区段的相对位置关系，分别推导出轮对间和收发端间的传输矩阵，最终建立列车由驶入至出清轨道电路区间的轨道电路多轮对动态分路模型。在ZPW-2000型轨道电路实验台上测取钢轨的一次参数并进行列车分路实验，将模型仿真数据与列车分路数据进行对比分析，分析多轮对分路模型轮对数量对仿真数据和模型性能的影响。研究结果表明：多轮对分路模型分路轮对数越接近实际分路情况，模型的精确性越高，验证了本文建模思想和模型的正确性。模拟2种常见的轨道电路故障，相对于现有单轮对模型，本文模型能够更好地模拟轨道电路工作情况，可为故障诊断研究提供更高质量的数据支持。

轨道电路；建模；多轮对分路；故障数据

轨道电路是铁路信号系统的重要设备之一，具有列车占用情况检测、完整性检查和向列车传输行车信息等功能。轨道电路一旦出现故障，轻则影响行车效率，重则造成人员伤亡。目前在轨道电路故障诊断研究中，通常需要大量的故障数据样本，但轨道电路发生故障的时间和位置具有随机性，且轨道电路微机监测系统采集的数据量大，筛选轨道电路故障数据存在一定难度。随着智能算法以及多信息融合的方法大量应用于轨道电路故障诊断[1−2]，对故障数据的需求越来越大，数据逐渐成为制约轨道电路故障诊断技术发展的瓶颈。已有研究表明，可以通过轨道电路模型模拟产生的故障数据代替现场数据来进行故障诊断研究[3−7]。张梦琪等[5]通过轨道电路模型分析分路不良故障对机车感应电流信号的影响。孙上鹏等[8−10]采用均匀传输线理论建立轨道电路调整和分路状态的模型，模拟轨道电路分路电流和轨出电压，并根据电流和电压曲线对补偿电容故障进行诊断。孙上鹏等[11]利用轨道电路模型产生的故障数据，实现了基于SVM算法的轨道电路故障智能诊断。以上针对轨道电路分路情形建模时，均采用单轮对(即一个等效的分路电阻并联于两段钢轨之间)模拟列车分路情形。Wakabayashi 等[12−13]通过在钢轨上进行分路实验，发现分路轮对个数的变化会引起分路电流的差异。当列车驶入轨道区间时，随着列车运行的位置变化，分路轮对数也将随之发生变化，从而引起钢轨输入阻抗变化，最终导致分路电流和轨出电压变化。因此，单轮对分路模型难以模拟列车真实的分路状态。本文针对ZPW-2000移频轨道电路，根据列车的真实分路情况，基于轮对与补偿电容和轨道区段的相对位置关系，分别推导出轮对间和收发端间的传输矩阵。分析列车从驶入轨道电路区间至驶出区间分路轮对数量的变化，在此基础上建立轨道电路多轮对动态分路模型。在ZPW-2000轨道电路实验台测量了钢轨的一次参数，并进行列车分路实验，测量列车分路时的分路电流和轨出电压实测数据。通过模型模拟数据与实测数据的对比分析，分析轮对数量对仿真数据和模型性能的影响，验证了本文建模思想和分路模型的正确性。在分路模型和实验台上模拟补偿电容开路和分路不良故障2种故障模式，通过分析，结果表明：相对于单轮对分路模型，本文模型能够产生更精确的故障数据，可为轨道电路故障诊断研究提供模型支持。

1 现有轨道电路单轮对分路模型

在现有文献中[3−4]，采用单轮对即一个分路电阻并联在钢轨两端来模拟列车分路轨道电路情形，列车分路轨道电路等效电路模型如图1所示。图中，g是从分路位置到轨道电路接收端的输入阻抗；g()是发送端到第1个轮对的传输矩阵；r()是最后1个轮对到接收端的传输矩阵；tc()是发送端到接收端的传输矩阵。

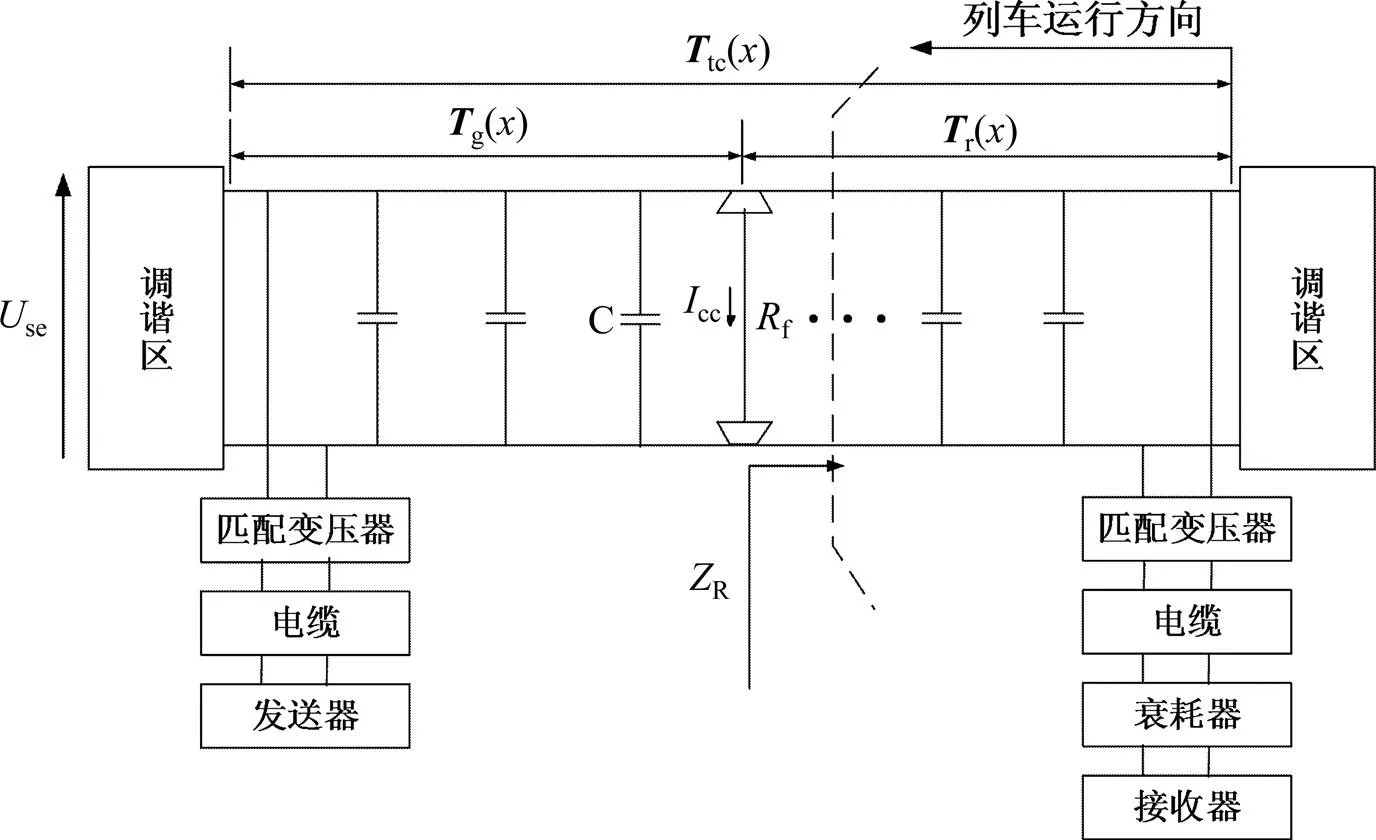
图1 ZPW-2000轨道电路分路示意图

设发送端和接收端的电缆等效传输矩阵分别为ca1和ca2，发送端和接收端的匹配变压器的等效传输矩阵分别为tr1和tr2，分路轮对的传输矩阵为Rf。则从发送器到接收器的传输矩阵tc如式(1)所示：

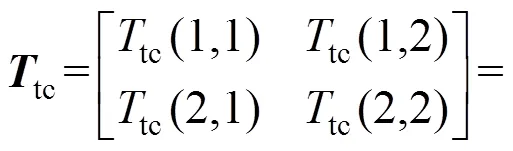
根据四端网性质，可得轨出电压re和分路电流cc如式(2)所示：

文献[12−13]通过实验验证了分路轮对的数量会引起轨面传输特性的变化，式(1~2)的单轮对分路模型不能有效地反映列车的真实分路情况。

2 轨道电路多轮对动态分路轨面建模

基于列车轮对与补偿电容和轨道区段的相对位置关系，推导出了2个轮对之间的传输矩阵，在此基础上根据列车运行的位置的变化，建立了多轮对动态分路模型。

2.1 2个轮对之间的传输矩阵

补偿电容在钢轨上是等间距安置的，故空闲的轨道电路轨面可看作是由多个补偿电容单元级联而成。补偿电容单元如图2所示。设一端轨道电路上安置了个补偿电容，补偿电容的安置间距为c，其中第1个和最后1个补偿电容分别距离发送端和接收端c/2。将补偿电容和其两边长为c/2钢轨单元看作一个补偿电容单元，如图2所示。

图2 补偿电容单元等效四端网络

图2中，x和c分别是长度为c/2的钢轨和补偿电容的传输矩阵，cc是一个补偿电容单元的传输矩阵。设和c分别为钢轨的传输系数和特性阻抗，则x，c和cc传输矩阵可以表示为：

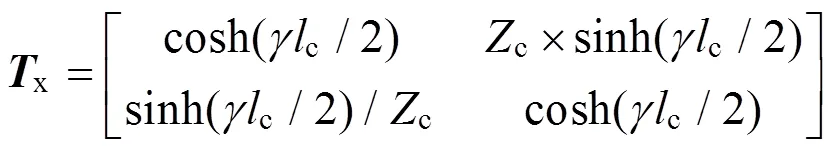
设轮对运行到第个补偿电容单元，则2个轮对与补偿电容的位置可分为3种(由于补偿电容最小设置间距大于列车任意2轮对间距)，如图3所示。

设2轮对间距为，补偿电容的间距为c。当补偿电容位于2轮对之间时，设第1个轮对和第2个轮对与补偿电容的距离分别为1和2，对应长度的钢轨传输矩阵分别为d1和d2，则2轮对之间钢轨的传输矩阵ld如式(6)所示：

2.2 基于分路位置的轨面建模

列车车体从驶入轨道电路区间至完全出清轨道电路区间过程中，分路轮对数量的变化趋势为先增加再保持不变然后逐渐减少。本节针对轨道电路发送端至接收端钢轨部分，建立四端网络模型。

图3 轮对与补偿电容位置关系示意图

以列车车体完全驶入轨道电路区间为例，对钢轨部分建模进行说明。列车车体完全驶入轨道电路区间时，如图4所示，分路轮对数量不随行驶距离发生变化。设发送端到第1个轮对的传输矩阵为g()，列车总轮对的个数为，第1个分路轮对到最后一个分路轮对的传输矩阵为D()，最后1个分路轮对到接收端的传输矩阵r()，第个轮对到发送端的距离为j，对应长度钢轨的传输矩阵 为ldj()。

图4 多轮对分路示意图

显然，当列车第1个轮对运行到第个补偿电容单元时，发送端到第1个轮对的传输矩阵g() 如式(7)所示：

第1个轮对到最后1个轮对之间的传输矩阵D()如式(8)所示：

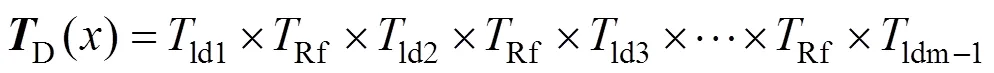
设1为最后1个轮对到接收端的距离，那么接收端的传输矩阵r()如式(9)所示：

由此可得出从发送器到接收器的传输矩阵tc如式(10)所示：

当钢轨驶入和驶出轨道电路区间时，分路轮对分别增加和减少，其矩阵形式和建模方法与列车车体完全驶入轨道电路区间基本一致，在此不作论述。

2.3 轨出电压Ure和分路电流Icc建模

在对轨道电路进行故障诊断研究时，常采用轨出电压和分路电流的数据判断轨道电路是否出现故障。本节根据前面提出的多轮对分路轨面模型，对轨出电压re和分路电流cc进行建模。

2.3.1 轨出电压re

设发送器发出的移频信号电压有效值为se，由传输矩阵性质，轨出电压re如式(11)所示：

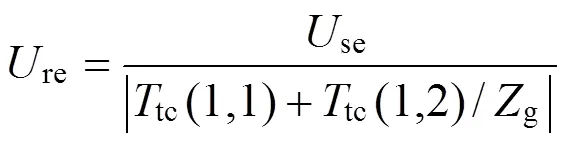
2.3.2 分路电流cc

考虑到列车的TCR安装在头车，TCR感应的是列车第1个轮对的分路电流，此处对第1个轮对的分路电流cc进行建模。列车驶入区间时四端网络模型如图5所示。图5中，Rf为分路电阻的传输矩阵，f2为第1个轮对与接收器之间的传输矩阵，等同于由D()，Rf，r()和re4个四端网络级联的传输矩阵。

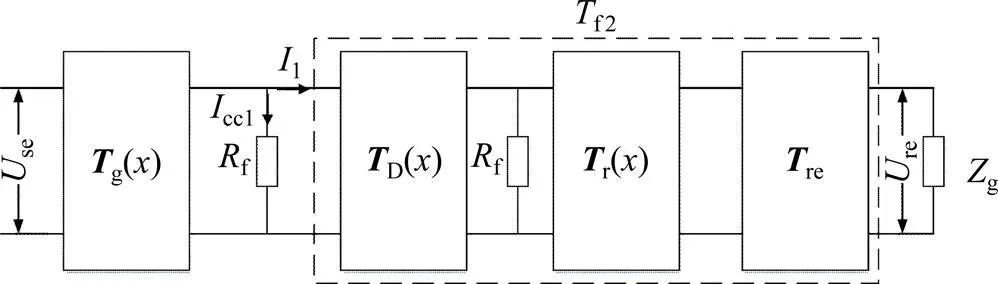
图5 列车在区间中行驶时等效四端网络

第1个轮对与接收器之间的传输矩阵f2如式(12)所示：

根据四端网络性质，分路电流cc和轨出电压re的关系如式(13)所示：

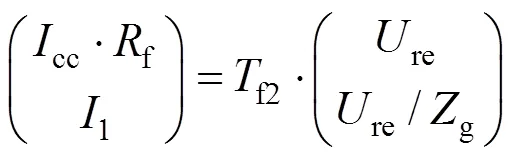
则第1个轮对的分路电流cc如式(14)所示：

3 实验台的参数测定

在ZPW-2000型轨道电路实验台上进行列车分路实验，测量分路电流和轨出电压的数据，用于验证本文提出的多轮对分路模型的正确性。为保证模型和实验台使用参数一致，首先对钢轨1次参数进行测量。

3.1 实验台参数测试

轨道电路实验台参数测量示意图如图6所示，钢轨外接220 V交流电源经变压器BG5进行供电。BG5的二次侧串联接入交流电流表，用于测量发送端电流。发送端和接收端两端分别并联交流电压表，用于测量发送端和接收端的电压。

图6 实验台轨道电路参数测试示意图

测试方法如下：

1) 将接收端开路，在发送端测量轨面电压s¥和送电电流s¥，同时在接收端测量轨出电压z¥；

2) 将接收端短路，测量发送端轨面电压s0和送电电流s0；

3) 测量轨道电路长度。

3.2 轨面一次参数计算

根据3.1中测量的数据，可计算出轨道电路实验台的一次传输参数。

1) 首先计算开路和短路时的输入阻抗模值：

开路时输入阻抗

短路时输入阻抗

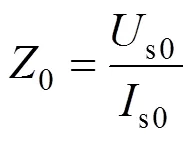
2) 根据式(15)~(16)可以计算出阻抗模值和传播系数：

特性阻抗

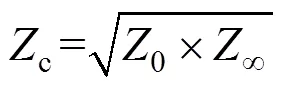
衰耗常数

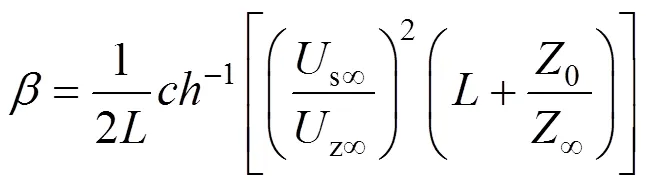
相移常数

传播系数

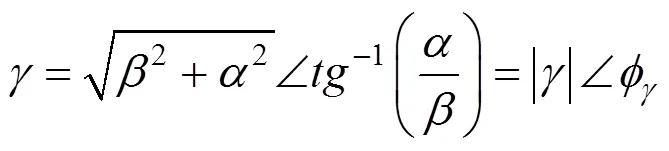
3) 根据式(17)~(20)可求得轨道电路的一次传输参数：

钢轨阻抗

道砟电阻

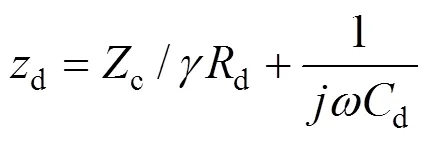
式(21~22)中：0，0，d和d分别为轨道电路的钢轨电阻、钢轨电感、道砟电阻和泄露电容；为发送端电源的载频。

经过相关测量和计算，得到轨道电路相关参数见表1所示。其中，分路实验采用的车型是CRH-2动车组，该车型由8节车厢组成(即有16个分路 轮对)。

表1 ZPW-2000轨道电路实验台一次参数

4 分路实验与模型对比分析

4.1 多轮对分路模型正确性验证

在实验台上进行列车分路实验，自列车匀速驶入接收端至出清发送端过程中，每隔40 m测量1次轨出电压和分路电流有效值，得到列车分路实测数据。保持与轨道电路实验台的参数一致，建立轨道电路多轮对分路模型，模拟列车分路过程。首先建立2轮对分路模型，在2轮对分路模型中，从发送端到第1个轮对的传输矩阵g2()如式(23)所示：

2个轮对之间钢轨的传输矩阵D2()如式(24)所示：

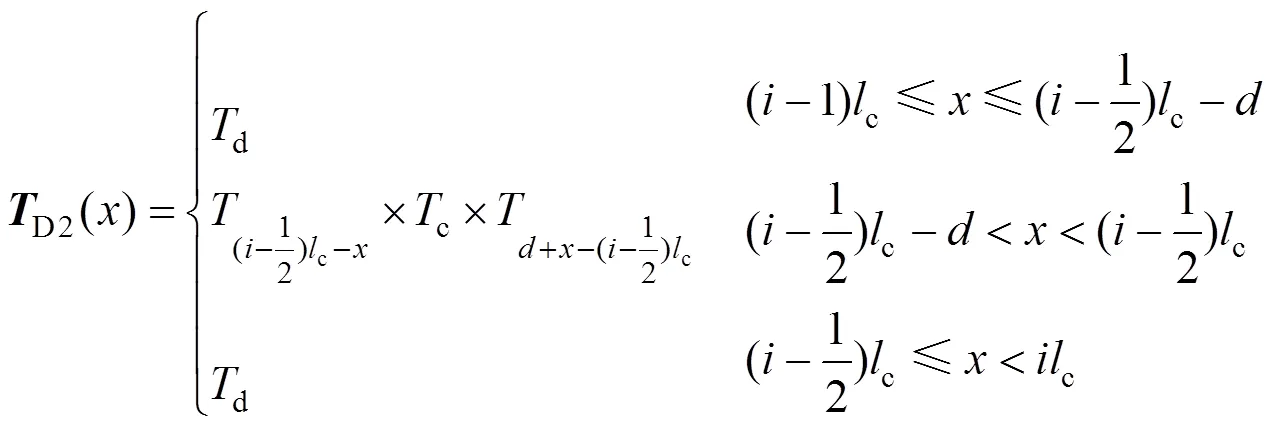
第2个轮对到接收端的传输矩阵r2()如式(25)所示：

根据g2()，D2()和r2()以及式(12~14)可得到2轮对分路的轨出电压和分路电流的解析式。在2轮对分路模型基础上，可推导出多轮对分路模型。

将列车分路实测数据、16轮对模型以及现有单轮对轨道电路分路模型(见式(1)~(2))仿真数据进行对比，分路电流、轨出电压的对比结果分别如图7~8所示。从图7和图8可以看出，16轮对模型仿真数据与列车分路实测数据较为接近，而单轮对模型与实测数据间存在明显误差，表明本文提出的多轮对模型能够更好地反映列车的分路情况。在列车自接收端向发送端运行过程中，由于分路轮对数量不断变化，改变了分路等效阻抗，自接收端起16轮对分路模型与单轮对模型的分路电流和轨出电压的差异逐渐增大。由于补偿电容的存在，单轮对模型分路电流从发送端到接收端呈现波浪式的衰减，16轮对模型的“波峰”则较平，而轨出电压包络变化趋势基本一致。在数值上，由于分路轮对的增加导致钢轨等效分路阻抗的减小，16轮对模型分路电流和轨出电压整体上小于单轮对模型分路电流和轨出电压。

图7 未发生故障分路电流的实测和仿真数据

图8 未发生故障轨出电压的实测和仿真数据

计算不同轮对分路模型仿真数据与列车分路实测数据之间的均方根误差，以表征仿真数据与实测数据之间的差异程度。均方根误差RE的计算公式如式(26)所示：

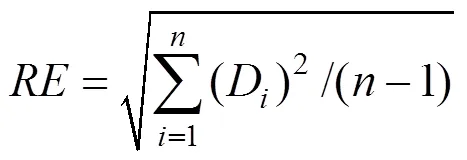
式中：D为第个测点仿真数据与实测数据之间的绝对误差；为实验台的测点个数。均方根误差RE越大，表明仿真数据与实测数据总体之间的差异越大。仿真数据与实测数据之间的均方根误差见表2所示。设仿真数据和实测数据之间的相对误差为δ，δ的计算公式如式(27)所示：

式(27)中：R为列车分路实验的实测数据。根据仿真数据和实测数据之间的相对误差绝对值||，绘制轨道电路未发生故障下不同分路轮对分路电流和轨出电压的相对误差盒状图，如图9所示。

从表2和图9可以看出，未发生故障的情况下，随着模型分路轮对数的增加，分路电流和轨出电压仿真数据与实测数据之间整体差异逐渐减小，相对误差及其离散程度不断降低。该结果表明分路模型轮对数越接近实际分路轮对数，模型精确性越高，验证了本文建模思想和模型的正确性。

表2 未发生故障时仿真数据与实测数据之间均方根误差

图9 未发生故障分路电流和轨出电压的相对误差盒状图

4.2 故障模拟

为研究故障情况下本文多轮对模型的有效性，本文在ZPW-2000轨道电路和多轮对分路模型上模拟了2种常见的轨道电路故障，并进行了对比分析。通过开路补偿电容C4以及增大钢轨接触电阻的方式[5]，在ZPW-2000轨道电路试验台上分别模拟补偿电容开路和分路不良2种故障模式，并进行列车分路实验，每隔40 m测量1次分路电流和轨出电压数据。通过测量，得到分路不良故障时单个轮对的分路电阻由0.31 Ω上升到0.5 Ω。

调节16轮对分路模型中参数，将第4个补偿电容和单个轮对分路电阻与上述分路实验保持一致，模拟补偿电容开路和分路不良故障。通过仿真，得到故障时的分路电流如图10所示。

图10 故障情况下16轮对模型分路电流包络

从图10可见，列车分路情况下，发生C4补偿电容开路故障时，该位置分路电流上升趋势消失，电流幅值平滑下降。C4的开路故障对接收端方向的分路电流数值产生影响，而对发送端方向分路电流几乎没有影响。发生分路不良故障时，分路电流包络形状基本不发生变化，但分路电流数值下降明显。采用HHT提取C4开路故障、分路不良故障以及轨道电路工作正常时分路电流的相位信息[3]，如图11所示。从图11可见，发生分路不良故障时，分路电流的相位信息与未发生故障时相同，均在补偿电容位置发生突变。而发生C4开路故障时，C4~C12段相位异常。由此可见，补偿电容开路故障会引起分路电流的相位异常。

通过模型产生C4开路、分路不良故障以及轨道电路正常时轨出电压曲线，如图12所示。从图12可见，发生第4个补偿电容开路故障时，自C4至C12，轨出电压包络有下降的趋势，而从C1到C4之间的轨出电压基本不发生变化。发生分路不良故障时，轨出电压包络明显上升，趋势不发生明显变化。以上结果可见，多轮对分路模型在发生故障时，模型产生的分路电流和轨出电压数据与轨道电路正常时有显著差异，可作为故障诊断的依据。

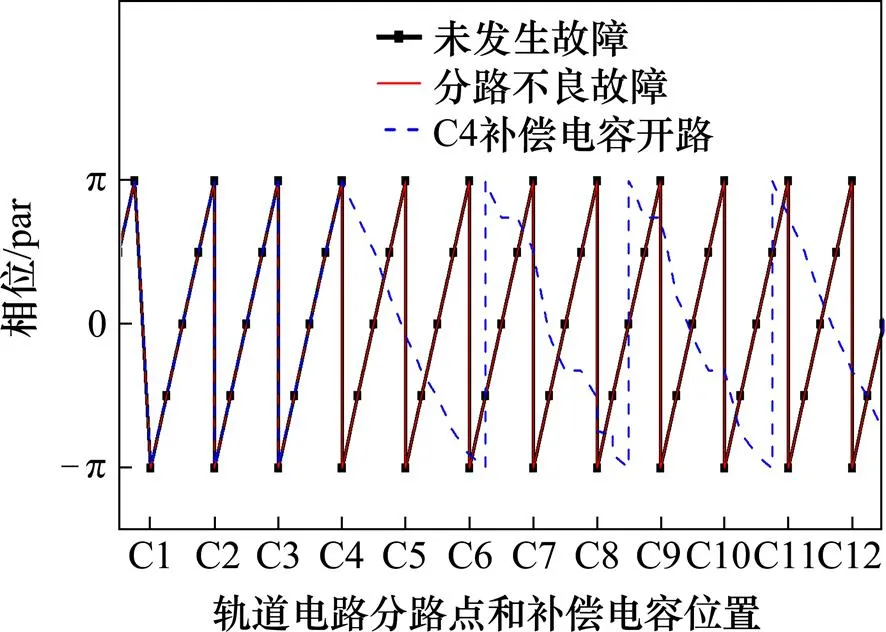
图11 HHT算法得到分路电流的相位信息

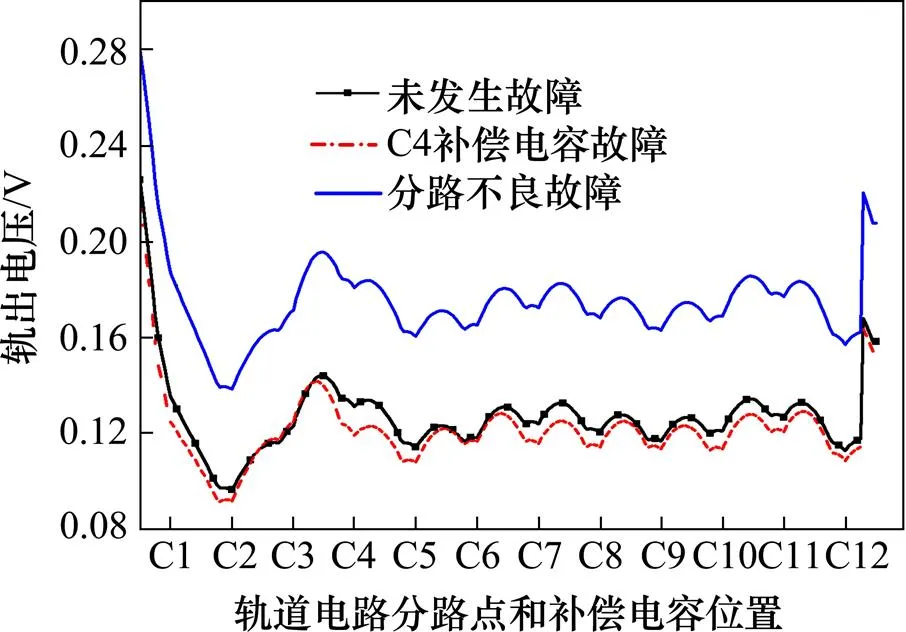
图12 故障情况下16轮对模型轨出电压包络

计算2种故障模式下不同分路轮对模型仿真数据与实测数据之间的均方根误差，见表3所示。做出仿真数据与实测数据间相对误差盒状图，如图13所示。从表3和图13可见，发生故障的情况下，模型分路轮对越多，仿真数据与实测数据之间整体差异越小，相对误差及其离散程度越低。16轮对分路模型在轨道电路发生故障情况下，各测点的分路电流和轨出电压相对误差分别低于5%和2%，可以很好地反映轨道电路故障情形。由此可见，相对于传统的单轮对分路模型，多轮对分路模型能更好模拟轨道电路故障情况，产生比单轮对模型更精确的故障数据，且模型分路轮对数越接近实际分路轮对数，模型产生的故障数据越接近真实故障数据，模型精确性越高。

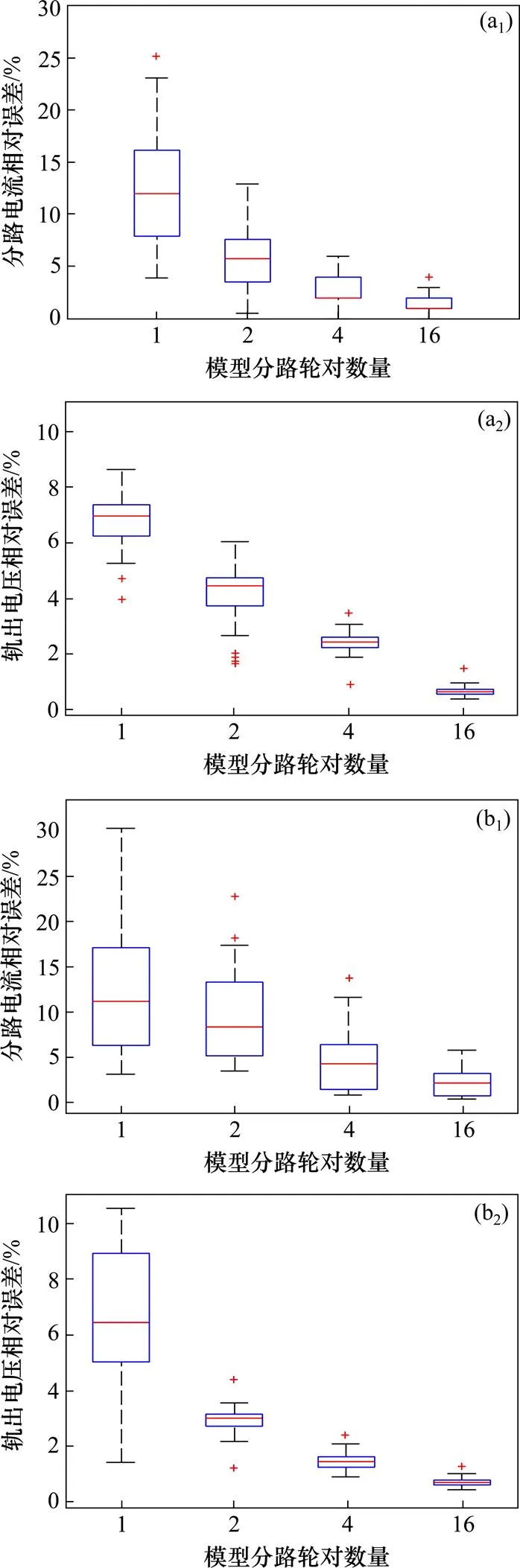
(a1), (a2) C4补偿电容开路故障；(b1), (b2) 分路不良故障

表3 发生故障时仿真数据与实测数据之间均方根误差

5 结论

1) 分析列车实际驶入轨道电路区间时轮对数量的变化，并基于列车轮对与补偿电容的位置关系，建立多轮对动态变化时的轨道电路分路模型。

2) 在ZPW-2000轨道电路进行列车分路实验，基于不同分路位置测取分路电流和轨出电压的数据，并与仿真数据进行对比验证，分析分路轮对数量变化对传输特性的影响。计算仿真数据和列车分路数据之间的均方根误差并绘出相对误差盒状图，经过分析，结果表明：多轮对分路模型轮对数越接近实际分路轮对数，模型的精确性越高，验证了本文建模思想和模型的正确性。

3) 模拟2种常见轨道电路故障，并进行误差分析，结果表明相对于现有单轮对分路模型，多轮对分路模型能产生更精确的故障数据，为轨道电路故障诊断提供模型支持。并且多轮对分路模型在模拟故障情况时，轮对数越接近实际分路轮对数，模型精确性越高，产生故障数据越可靠。

[1] 李娜, 董海鹰. 基于D-S证据理论信息融合的轨道电路故障诊断方法研究[J]. 铁道科学与工程学报, 2012, 9(6): 107−112. LI Na, DONG Haiying. Research on track circuit fault diagnosis method based on D-S evidence theory information fusion[J]. Journal of Railway Science and Engineering, 2012, 9(6): 107−112.

[2] 陆晓峰, 王小敏, 李光耀. 基于Mamdani模糊神经网络的相敏轨道电路故障诊断方法研究[J]. 铁道标准设计, 2015(11): 104−109. LU Xiaofeng, WANG xiaomin, LI Guangyao. Research on phase-sensitive track circuit fault diagnosis based on mamdani fuzzy neural network[J]. Railway Standard Design, 2015(11): 104−109.

[3] 赵林海, 蔡伯根, 邱宽民,等. 基于HHT、DBWT的无绝缘轨道电路补偿电容故障诊断[J]. 铁道学报, 2011, 33(3): 49−54. ZHAO Linhai, CAI Bogen, QIU Kuanmin, et al. The method of diagnosis of compensation capacitor failures with jointless track circuits based on HHT and DBWT[J]. Journal of the China Railway Society, 2011, 33(3): 49− 54.

[4] 赵林海, 许俊杰, 刘伟宁,等. 基于Levenberg- Marquardt算法和广义S-变换的无绝缘轨道电路补偿电容的故障检测[J]. 控制理论与应用, 2010, 27(12): 1612−1617. ZHAO Linhai, XU Junjie, LIU Weining, et al. Compensation capacitor fault detection method in jointless track circuit based on Levenberg-Marquardt algorithm and generalized S-transform[J]. Control Theory and Applications, 2010, 27(12): 1612−1617.

[5] 张梦琪, 赵会兵, 孙上鹏. 基于粒子群支持向量机的轨道电路分路不良预测方法[J]. 铁道学报, 2015, 37(10): 68−74. ZHANG Mengqi, ZHAO Huibing, SUN Shangpeng. Prediction of shunt malfunction of track circuit based on PSO-SVM[J]. Journal of the China Railway Society, 2015, 37(10): 68−74.

[6] 黄赞武, 魏学业, 刘泽. 基于模糊神经网络的轨道电路故障诊断方法研究[J]. 铁道学报, 2012, 34(11): 54−59. HUANG Zanwu, WEI Xueye, LIU Ze. Fault diagnosis of railway track circuit using fuzzy neural network[J]. Journal of the China Railway Society, 2012, 34(11): 54−59.

[7] WANG Xiaomin, GUO Jin, JIANG Lei, et al. Intelligent fault diagnosis and prediction technologies for condition based maintenance of track circuit[C]// IEEE International Conference on Intelligent Rail Transportation, 2016.

[8] 孙上鹏, 赵会兵. 基于相空间重构的无绝缘轨道电路补偿电容故障检测方法[J]. 铁道学报, 2012, 34(10): 79−84. SUN Shangpeng, ZHAO Huibing. The method of fault detection of compensation in jointless track circuit based on phase space reconstruction[J]. Journal of the China Railway Society, 2012, 34(10): 79−84.

[9] 贾晨子, 刘彦堂, 杨世武. 移频轨道电路模型建立及应用[J]. 铁路计算机应用, 2007, 16(4): 34−35. JIA Chenzi, LIU Yantang, YANG Shiwu. Establishment and application of model for frequency-shift track circuit[J]. Railway Computer Application, 2007, 16(4): 34−35.

[10] 秦利国, 何潇, 李娟, 等. 轨道电路补偿电容断路故障诊断[C]// 第25届中国控制与决策会议, 贵阳, 2013: 4869−4873. QING Liguo, HE Xiao, LI Juan, et al. Fault diagnisis for open component capacitor in track circuits[C]// the 25th Chinese Control and Decision Conference, Guiyang, 2013: 4869−4873.

[11] 孙上鹏. 无绝缘轨道电路故障诊断方法研究[D]. 北京:北京交通大学, 2014. SUN Shangpeng. Research on fault diagnosis for railway jointless track circuits[D]. Beijing: Beijing Jiaotong University, 2014.

[12] Wakabayashi Y, Nakagawa D, Kitagawa T, et al. Influence of contact condition between rails and wheels upon track circuit shunting. 3rd report. electric resonance phenomena by track circuit shunting of running train’s wheelset[J]. Transactions of the Japan Society of Mechanical Engineers, 2002, 68(10): 3023−3028.

[13] Hirama J, Wakabayashi Y, Kitagawa T, et al. Influence of contact condition between rails and wheels upon track circuit shunting (4th Report, Result of Continuously Measured Shunting Resistance of the Running Wheelsets): 4th Report, Result of Continuously Measured Shunting Resistance of the Running Wheelset[J]. Advances in Structural Engineering, 2005, 71(4):1263−1268.

(编辑 阳丽霞)

Research on dynamic multi-wheel sets shunted track circuit modeling

FU Jiawei, WANG Xiaomin, GUO Jin

(School of Information Science and Technology, the Key Laboratory of Traffic Information Engineering and Control, Southwest Jiaotong University, Chengdu 611756, China)

Aiming at the shortcomings that ZPW-2000 track circuit single-wheel-shunt model is difficult to reflect the real shunted situation, a new modeling method of track circuit based on dynamic multi-wheel setsshunting was proposed in this paper. Based on the positional relationship of the wheelset , the compensation capacitor and track section, the transmission matrix of wheel sets, transmitter and reciever was deduced. Finally, the dynamic multi-wheel sets shunted model in the process of entering and pulling out the track circuit was established. Primary parameters and shunted test data was measured on ZPW-2000 test bed, and the influence of quantity of shunted wheel sets on simulated data and model performance was analyzed through the the comparative analysis of the simulated data and test data. As a result, the nearer quantity of shunted wheel sets on multi-wheel sets shunted model approximates to real shunted condition, the higher accuracy of model is, the modeling idea and validity of multi-wheel sets shunted model in this paper is verified. Two kinds of track circuit fault were simulated. The results shows that compared with the single-wheel set shunted model, multi-wheel sets model matches the practice better and provides more accurate data to support fault diagnosis of track circuit.

track circuit; modeling; multi-wheel sets shunt; fault data

10.19713/j.cnki.43−1423/u.2018.09.026

U284.22

A

1672 − 7029(2018)09 − 2374 − 11

2017−06−25

国家自然科学基金资助项目(61371098)；四川省应用基础研究资助项目(2015JY0182)；中央高校基本科研业务费专项资金资助项目(2682017ZDPY10)

王小敏(1974−)，男，江西萍乡人，教授，博士，从事铁路信号运维与安全工程方向研究；E−mail：xmwang@swjtu.edu.cn