基于权矩阵的通风网络最小生成树算法研究

涂鹏，张恒，孙建春，王路



基于权矩阵的通风网络最小生成树算法研究

涂鹏1, 2，张恒1，孙建春1，王路2

(1. 西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；2. 四川交通职业技术学院 道路与桥梁工程系，四川 成都 611130)

为优化图的数据存储结构，缩小最小生成树构造过程的搜寻范围，提高搜索效率，减小构造过程中的判断，以赋权有向图权矩阵为基础，结合最小生成树性质提出用于存储通风网络数据的表格，并将表格进行分区处理。基于Prim算法和通风网络数据存储结构，提出通风网络最小生成树构造方法并编制相应程序，结合具体通风网络结构以表格方式给出最小生成树的具体构成过程。研究结果表明：基于权矩阵的构造方法与经典Prim算法对工程算例的最小生成树进行构造分析所得到结果是一致的，同时编制的程序也验证了该方法能够正确有效地构造通风网络最小生成树。

通风网络；最小生成树；Prim算法；权矩阵

最小生成树在图论分析中具有重要的意义，因此国内外学者对此问题进行了深入的研究。在研究无向赋权图的最小生成树方面，最为常用的是避圈法，其代表算法有Kruskal算法、Prim算法及Dijkstra提出的最小生成树算法[1]。避圈法在生成最小生成过程避免选择的边组成回路，国内学者从相反的思路出发，在构造最小生成树的过程中通过删除回路上的最大权值边，破除图中的回路，使得图中不存在回路，从而得到图的最小生成树，因为在最小生成树的构造过程不断破除图中的“圈”，因此称该方法为破圈法[2−3]。可以看出避圈法和破圈法一个是“加法”一个是“减法”，前者通过将要“加”的边放进最小树生成树边集中得到最小生成树，而后者则是通过对原图进行“减”后得到最小生成树，无论是避圈法还是破圈法，在最小生成树的构造过程中，都涉及大量的判断。通风网络作为典型的赋权有向图，其最小生成树问题研究成果较少。吴文虎等[4]通过研究有向赋权图的有向圈的收缩及展开，对有向赋权图的最小生成树构造进行了一定的研究。冯俊文[5]提出了赋权有向图的表格表示法，并基于该表格给出了一种求解最小生成树的表上作业法，但采用该表构成最小生成树的过程中涉及大量的判断及边的搜寻，范围较大，存在效率低的问题。王义章[6]通过对Waissi算法进行改进，提出了一种时间复杂度为(2)的通风网络最小生成树算法，该算法中也涉及到较多的判断。孙凌宇等[7]基于赋权有向图的最小生成树性质对Prim算法及Kruskal算法进行了改进，提出了最小生成树的改进算法，但是未给出赋权有向图数据的存储结构，无法判断算法中边的搜索效率。袁威威[8]通过对Kruskal算法进行改进提出了一种改进的MST生成算法，该算法虽然减小了对边的搜索范围，但加大了对节点的搜索，同时也存在大量的判断。徐建军等[9]根据最小生成树的性质及定义提出了一种新的最小生成树算法，该算法能够有效提高搜寻效率，但要求程序具有较高的判断能力，编程难度相对较大。综上可知，优化图的数据存储结构，减小最小生成树构造过程的搜寻范围，提高搜索效率，减小构造过程中的判断成为通风网络最小生成树构造方法的优化方向。

1 通风网络及其最小生成树

通风网络是一个有向网络，通风网络中各分支的方向由风流方向决定。通常以进风口为网络的起始节点，出风口为终结点，进风口与出风口均为大气节点[9−11]。

在通风网络分析中，图论具有重要的作用，图的本质内容是顶点和边的联接关系，也称为拓扑结构关系。通常采用矩阵来表述图中的联接关系，对于赋权图而言，权矩阵不仅能够反映边与顶点的联接关系，还能够清楚的反映图中各边的权值大小，权矩阵的定义如下：

设=(,)是一个通风网络，图=(,)是一个连通图，||=节点数，||=边数，=(w,j)是一个×矩阵，行序标识为边的始节点，列序标识为的末节点，w,j为联接节点,的边的权值，即为该通风网络的权矩阵。

在通风网络分析中，风网的解算、优化及调节都和生成树存在密切的关系，因此通风网络中生成树的选择对于风网分析至关重要。生成树的定义为：不含回路的连通图，换言之，从生成树的任一节点沿着生成树的边都不能回到原点，但可以到达除原点外的其他节点。从生成树的定义可知，通风网络的生成树包含通风网络的全部节点及部分边，用数学语言描述即为：图=(,)是一个通风网络图，T是的一棵生成树，则T=(,E)，EÍE。

将生成树T对应的所有边的风阻值累加值作为该生成树的风阻值，记为(T)。从生成树的定义可知，通风网络的生成树不是唯一的，生成树的风阻值也不是唯一的，必定存在一个最小值，通常将最小值对应的生成树称为该通风网络的最小生成树。

2 最小生成树性质及Prim算法

最小生成树性质如下：设=(,)是一个连通图，顶点集是的真子集(可以任意选取)，CU为顶点集的补集。顶点Î，ÎCU，(,)表示通风网络图中联接点集与CU的边集，即(,)Î，记边集(,)中权值最小的边为<,，则一定存在的一棵最小生成树，它以<,为其中一条边。

该性质证明如下：

假设为图=(,)的任意一颗最小生成树，根据生成树定义可知，图与最小生成树的拥有相同的顶点集。将顶点集分成2部分和CU，(,)为横跨这2个点集的边集，<,为(,)中权值最小的边，当不包含边<,时，将<,添加到树中，根据生产树的定义可知，添加一条边后生成树必定含有回路，因此树将变为含回路的子图，并且该回路上有一条不同于<,的边<′,′>,′Î,′ÎCU。将<′,′>删去，得到另一颗树′，即树′是通过将中的边<′,′>替换为<,>得到的。由于<,>边的权值小于<′,′>边，故生成树′的权值小于生成树，这与是任意最小生成树的假设相矛盾，从而得证。

Robert C. Prim在该性质的启发下，采用贪心算法提出了用于构造最小生成树的Pirm算法。该算法可表述为：设=(,)是一个连通图，图的最小生成树记为，Î为已被选择的点集，−为连通图中待选的点集，每次选择连接点集与−的权值最小的边<,>，并将其放入中，直到=时，停止搜寻。

不难发现，Prim算法构造最小生成树的过程中，每次选择最小生成树的边时都运用了最小生成树的性质，因此所选的边也必定是最小生成树的边。根据生成树的性质可知，Prim算法选择的边集必能构成最小生成树。

3 通风网络最小生成树启发式构造法

算法与数据结构间联系密切，算法影响着数据结构的构造，而数据结构又是算法的基础，因此，一个优秀的算法背后必定存在一个结构合理的数据结构[12−14]。受Prim算法启示，本文提出了一种利用基于权矩阵的表格来构造最小生成树的方法。

权矩阵采用行标和列标表示通风网络中风支的起点和终点，当对权矩阵行及列元素进行变换，变换后的权矩阵的行标及列标无法再反映风支的起点和终点关系，为了能够在变换后依旧能够反映元素对应边的起点和终点关系，本文提出一种用于表示通风网络图的表，该表在权矩阵的基础上增加一行及一列，增加的行及列用于记录风支的终点和起点编号，如表1所示。

表1 通风网络的表格表示

2个节点间无直接联接时，对应边的权值以¥代替，当2点间的直接联接边超过1条时，对应位置填写最小权值。将该表简记为=(,)，称该表为通风网络=(,)的表，如表2所示。

表2 通风网络表的分区

Table 2 Partition of ventilation network table

为了表述方便，将表格进行分区表示，Ⅰ区为已选节点组成的局部表，记为Ⅰ=(,W)；Ⅱ区为未被选中节点组成的局部表，记为Ⅱ=(−,W−U)；Ⅲ区为以节点集中的节点为起点，以节点集−中的节点为终点组成的局部表，记为Ⅲ=(,W,V−)；Ⅳ区为以节点集−中的节点为起点，以节点集中的节点为终点组成的局部表，记为Ⅳ=(,W−,U)。

由于最小生成树的构造过程中，与−处于变化中，因此，元素在各分区的分布也随着最小生成树的构造过程发生变化。结合最小生成树的性质可知，在给定时，最小生成树的边只存于Ⅲ和Ⅳ区中，不可能存在于Ⅰ和Ⅱ区。因此可知对通风网络表进行上述分区能够有效锁定最小生成树边的范围，减小搜寻量，提高搜寻效率。搜索效率提高程度与网络结构密切相关，网络权矩阵越稀疏，效率的提高越小；反之，效率的提高越明显。因此，采用本文构造的通风网络表求解最小生成树的具体过程如下：

第1步：将通风网络的起点放入点集中，在对应的Ⅲ和Ⅳ区中选择值最小的元素；

第2步：将新选择的节点放入点集中，将对应的边放入中；

第3步：||是否等于|V|；

第4步：第3步满足要求则完成通风网络最小生成树的构造，否则，调整表格后按照第1，2和3步顺序循环。

表格的调整方法有多种，本文采用的方法如表3和表4所示。若节点1，2，3已被记入点集中，则此时通风网络表的Ⅲ和Ⅳ区如表3所示；若2,n为Ⅲ和Ⅳ区中值最小的元素，将第4列与第列进行调换，第4行与第行进行调换，调换后的表如表4所示。

表3 通风网络表的调整方式

Table 3 Adjustment mode of ventilation network table

依据本文提出的通风网络最小生成树构造方法，采用C#语言编制了相关的程序，其操作界面如图1所示，界面包含1个数据输入框及3个按钮键，将通风网络数据按照“起点号，终点号，权值；起点号，终点号，权值…；起点号，终点号，权值”格式输入数据输入框，按下“添加”键完成通风网络数据的输入操作；按下“显示通风网络表”键后则可以查看通风网络表；按下“输出最小生成树”键则可以得到通风网络的最小生成树。MST程序不仅适用于小型风网最小生成树的求解，同时也能够用于生成大型风网的最小生成树；与较传统方法相比，风网结构越复杂，最小生成树的生成效率越高。搜索效率示意图如图2所示，黑色节点代表已选节点，共6个，灰色为待选节点，共4个；共16条边。因为6个节点需5条边才能连起来，故黑线中应该有5条边已经被选取。按照传统方法共计11条边为搜寻范围，而采用分区方法后只需要搜寻5条边(粗线部分)。

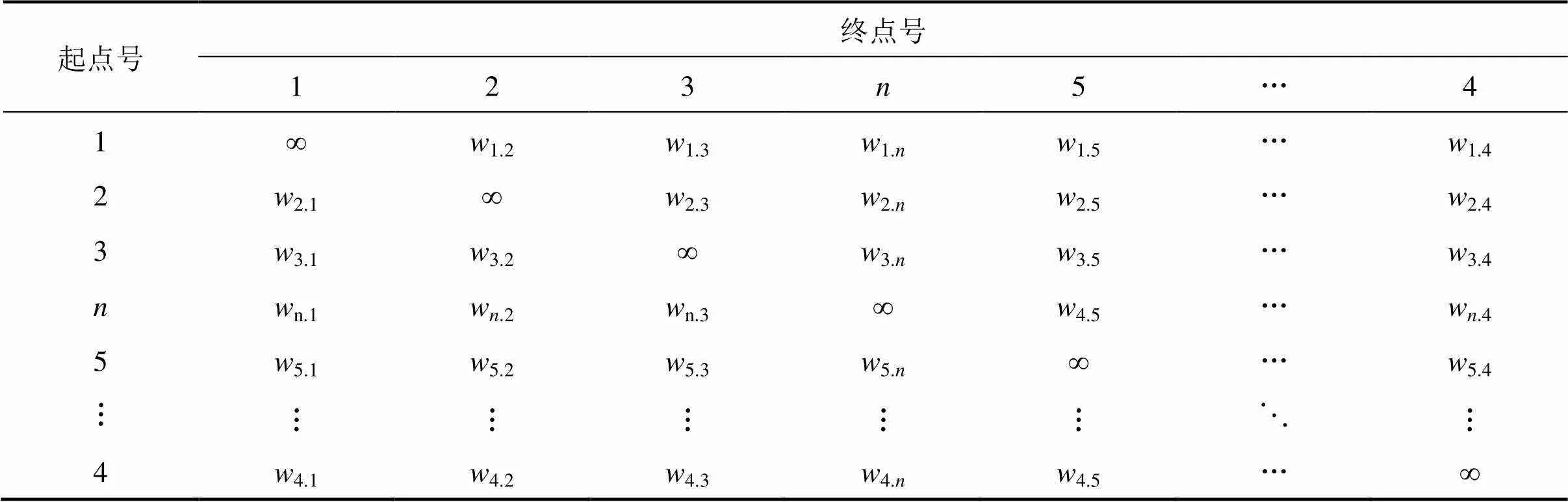
表4 调整后的通风网络表

图1 最小生成树生成软件操作界面

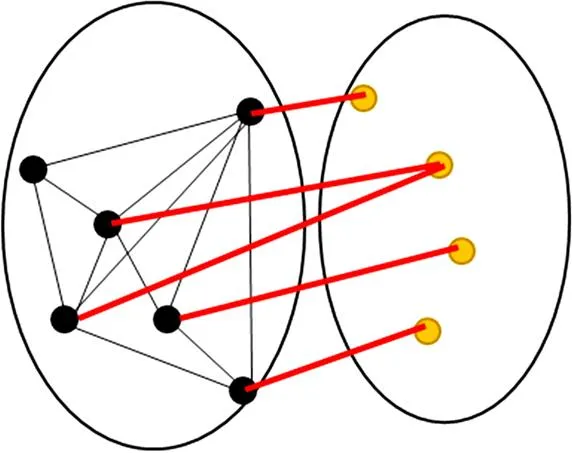
图2 搜索效率示意图

4 工程算例分析

以文献[15]中的通风网络图为工程背景，对本文提出的通风网络最小生成树构造方法进行分析，并与文献[6]结果进行对比验证。通风网络中共计12个节点(通风网络的起点及终点视为2个节点)，19条分支。其中节点9与节点10间存在2条分支，各分支对应的权值见图2所示。

根据本文规定将各分支的权值记入图3所示通风网络表中，得到图3所示通风网络表如表5所示。

图4为图3所示通风网络最小生成树的Prim算法。从通风网络图中任选一节点作为最小生成树构造过程中的已选节点(节点1)，如图4(a)所示；扫描与节点1联接的边，找到权值最小的边<1,3>，将该分支作为最小生成的边绘制在图中，如图4(b)所示；扫描与节点1、3联接的边，选择权值最小的(不包含已选边)边<3,6>，同样作为最小生成的边绘制在图中，如图4(c)所示；扫描与节点1，3和6联接的边，选择权值最小的边作为最小生成树的边绘制在图3中，如此循环，直到图4包含图3的所有节点才结束循环，完成通风网络最小生成树的构造过程。图4(i)即为图3所示通风网络的一棵最小生成树。该生成树包含的边为：<1,3>，<3,6>，<6,5>，<5,8>，<6,7>，<1,2>，<7,9>，<9,10>，<10,11>，<11,12>，<4,12>，权值为0.206 62。

图3 算例的风路风阻

表5 算例通风网络表

图4 算例通风网络最小生成树形成过程图

表6为采用本文提出的最小生成树的构造方法得到的图3所示通风网络的最小生成树的构造过程，对比表6与图3可知，表6是图3的表格表现形式，而图3是表6的图的表现形式，其对应关系如表7所示。表7也从另一个方面证明了本文提出的通风网络最小生成树的构成方法是可行的。

表6 工程算例最小生成树构造过程表

表7 图3与表6对应关系表

注：为了表述简洁，表中对图编号进行简写，如5 a)简写为a)

采用本文提出的方法及Prim算法得出的图3所示的通风网络的最小生成树的权值为0.206 62。而文献[6]得到的最小生成树为：{<1,3>,<1,2><3,6>, <2,4>,<6,5>,<6.7>,<4,12>,<5,8>,<7,9>,<9,10>,<10,11>}，对应的权值为0.368 82。对比可知采用本文方法得到的图3的最小生成树权值较文献[6]得到的最小生成树权值要小，文献[6]采用除通风网络的起始节点外，其他节点入度(以该节点为末节点的边数目)为1作为算法的控制条件，得出了图3所示的通风网络的最小生成树。而根据图3可知，通风网络的最小生成树的节点的入度可以不为1(图3节点12的入度为2)，因此采用节点入度控制方法不能确保所选的边为最小生成树的边。

图5为根据本文提出的最小生成树构造法编制的程序得出的图3所示通风网络的最小生成树，与表6结果一致。表明该程序编制正确，能够正确求解通风网络的最小生成树。

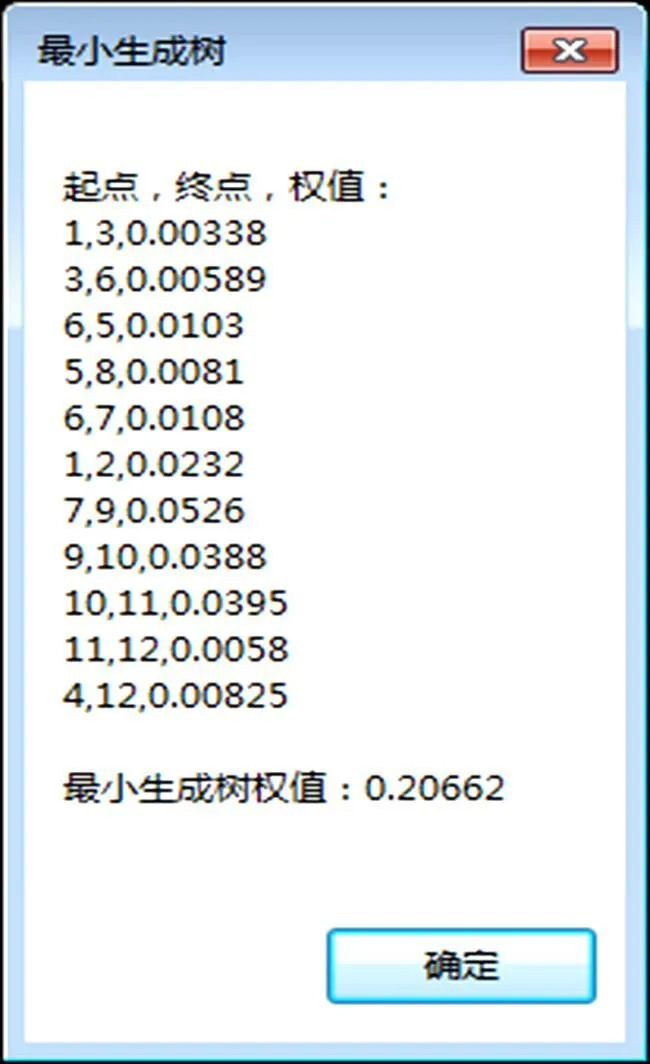
图5 软件生成的最小生成树

5 结论

1) 通过在通风网络图的权矩阵中增加一行及一列用于记录通风网络分支的起点编号及终点编号，提出了用于表示通风网络的表。

2) 为了减小通风网络最小生成树构造过程中边的搜寻范围，根据最小生成树的性质将通风网络表进行了分区处理，从而将搜寻范围限定在表中的III、IV区，极大的减小了最小生成树构成过程中的搜索范围，提高了搜索效率。

3) 基于权矩阵的构造方法与经典Prim算法对工程算例的最小生成树进行了构造分析所得到结果是一致的，同时编制的程序也验证了该方法能够正确有效的构造通风网络最小生成树。

基于权矩阵的通风网络最小生成树构造方法虽然缩小了最小生成树生成过程中的搜寻范围，提高了搜寻效率，但是对于稀疏权矩阵而言，由于存在大量的权值为∞的元素，导致搜寻效率不高，因此，如何提高稀疏权矩阵的搜寻效率需要进一步研究。由于Kruskal算法对于稀疏矩阵有着显著优势，可尝试采用本文方法来改进Kruskal算法，从而扩大算法的适应性。

[1] 卢开澄, 卢明华. 图论及其应用[M]. 北京: 清华大学出版社, 1995. LU Kaicheng, LU Minghua. Graph theory and its application[M]. Beijing: Tsinghua University Press, 1995.

[2] 董跃华, 李云浩, 姜在东. 用破圈法实现普里姆算法[J]. 江西理工大学学报, 2008(4): 20−22. DONG Yuehua, LI Yunhao, JIANG Zaidong. Realize prim algorithm with the breaking circle way[J]. Journal of Jiangxi University of Science and Technology, 2008(4): 20−22.

[3] 秦彦新, 王越光. 用“破圈法”求全部最小生成树的算法[J]. 空军雷达学院学报, 2006(2): 134−137. QIN Yanxin, WANG Yueguang. Algorithm of finding all minimum spanning trees by breaking loop[J]. Journal of Air Force Radar Academy, 2006(2): 134−137.

[4] 吴文虎, 王建德. 信息学奥林匹克竞赛指导——图论的算法与程序设计[M]. 北京: 清华大学出版社, 1997. WU Wenhu, WANG Jiande. Information olympiad competition guidance-graph theory and programming [M]. Beijing: Tsinghua University Press, 1997.

[5] 冯俊文. 赋权有向图最小生成树的表上作业法[J]. 系统工程与电子技术, 1998, 8(6): 26−29. FENG Junwen. Table operations method for minimum spanning trees problem in weighted digraph[J]. Systems Engineering and Electronics, 1998, 8(6): 26−29.

[6] 王义章. 通风网络中最小生成树的(~2)算法[J]. 贵州科学, 1995(2): 15−20. WANG Yizhang. The algorithm of(~2) minimum spanning tree and its application in ventilation networks [J]. Guizhou Science, 1995(2): 15−20.

[7] 孙凌宇, 冷明, 谭云兰, 等. 赋权有向图的最小生成树算法[J]. 计算机工程, 2010(2): 61−63, 66. SUN Lingyu, LENG Ming, TAN Yunlan, et al. Minimum spanning tree algorithm for weighted directed graph [J]. Computer Engineering, 2010(2): 61−63, 66.

[8] 袁威威. 应用Kruskal的改进算法求最小生成树[J]. 江苏第二师范学院学报, 2017, 33(6): 12−13. YUAN Weiwei. Application of Kruskal’s Improved algorithm to find minimum spanning tree[J]. Journal of Jiangsu Second Normal University (Natural Science), 2017, 33(6): 12−13.

[9] 徐建军, 沙力妮, 张艳, 等. 一种新的最小生成树算法[J]. 电力系统保护与控制, 2011, 39(14): 107−112. XU Jianjun, SHA Lini, ZHANG Yan, et al. A new algorithm for minimum spanning tree[J]. Power System Protection and Control, 2011, 39(14): 107−112.

[10] 钟德云, 王李管, 毕林, 等. 基于回路风量法的复杂矿井通风网络解算算法[J]. 煤炭学报, 2015, 40(2): 365−370. ZHONG Deyun, WANG Liguan, BI Lin, et al. Algorithm of complex ventilation network solution based on circuit air-quantity method[J]. Journal of China Coal Society, 2015, 40(2): 365−370.

[11] Zhong C, Miao D, Wang R. A graph-theoretical clustering method based on two rounds of minimum spanning trees[J]. Pattern Recognition, 2010, 43 (3): 752−766.

[12] Jothi R, Mohanty S K, Ojha A. Functional grouping of imilar genes using eigenanalysis on minimum spanning tree based neighborhood graph[J]. Computers in Biology and Medicine, 2016, 71(4): 135−148.

[13] WU J, LI X, Jiao L, et al. Minimum spanning trees for community detection[J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(9): 2265−2277.

[14] Pirim H, Ekşioğlu B, Perkins A D. Clustering high throughput biological data with B-MST, a minimum spanning tree based heuristic[J]. Computers in Biology and Medicine, 2015, 62(7): 94−102.

[15] 李恕和, 王义章. 矿井通风网络计算的牛顿法[J]. 煤炭学报, 1982(4): 52−62. LI Shuhe, WANG Yizhang. The newton method for calculating the mine ventilation networks[J]. Journal of China Coal Society, 1982(4): 52−62.

(编辑 涂鹏)

A study on minimum spanning tree algorithm of ventilation network based on weight matrix

TU Peng1, 2, ZHANG Heng1, SUN Jianchun1, WANG Lu2

(1. Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China; 2. Sichuan Vocational and Technical College of Communications, Chengdu, 611130, China)

In order to optimize the data storage structure of the graph, narrow the search range of the minimum spanning tree construction process, improve the search efficiency and reduce the judgment in the construction process, based on weight matrices of weighted directed graph and combined properties of minimum spanning tree, a table for storing ventilation network data was proposed and partitioned. Based on the Prim algorithm and data storage structure of ventilation network, the minimum spanning tree construction method was proposed and the corresponding program was developed. In combination with the specific ventilation network structure, the process of minimum spanning tree was given in tabular form. The results show that the construction method based on weight matrix for analyzing the minimum spanning tree of an engineering example is consistent with the classical Prim algorithm. The program also proves that the method can correctly and effectively construct the minimum spanning tree of the ventilation network.

ventilation network; minimum spanning tree; Prim algorithm; weight matrix

10.19713/j.cnki.43−1423/u.2018.09.015

TD725

A

1672 − 7029(2018)09 − 2285 − 08

2017−07−17

国家自然科学基金资助项目(51508477)；中央高校基本科研业务费专项资金资助项目(2682016CX012)

张恒(1985−)，男，贵州铜仁人，讲师，博士，从事隧道及地下工程通风与防灾研究；E−mail：tunnelzh@home.swjtu.edu.cn