基于支持向量机的CRTS Ⅱ型板式无砟轨道板正温度梯度预警方法

郭云祺，李再帏, 2, 3，何越磊，路宏遥



基于支持向量机的CRTS Ⅱ型板式无砟轨道板正温度梯度预警方法

郭云祺1，李再帏1, 2, 3，何越磊1，路宏遥1

(1. 上海工程技术大学 城市轨道交通学院, 上海 201620；2. 华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013；3. 北京交通大学 土木建筑工程学院，北京 100044)

无砟轨道板温度梯度是温度荷载作用在轨道结构上的重要表征，也是结构设计和养护维修的关键参数。针对轨道板温度梯度状态监测预警问题，基于运营线实测高铁轨道板数据样本，以气温、太阳辐射、风速等气象参数为特征输入参量，轨道板正温度梯度为输出参量，建立基于支持向量机的轨道板正温度梯度分类预警模型，给出模型关键性参数的选择方法；利用实测数据验证预警模型的有效性和准确性，并结合历史气象资料数据，采用所建立模型确定气象参数的预警阈值。研究结果表明：无砟轨道板正温度梯度预警模型识别准确率为98.648 6%，气温、太阳辐射量、风速的预警指标值为33.9 ℃，733 W/m2和2 m/s且可靠性为96%，可为轨道结构的设计改进、病害预防以及养护维修提供方向性指导与建议。

高速铁路；无砟轨道；温度梯度；支持向量机；分类预警

CRTSⅡ型板式无砟轨道是我国高速铁路使用最为广泛的轨道结构之一，其长期暴露在大气环境下，内部温度分布主要受外界气象参数影响[1]；特别是在极端高温天气下，轨道板内部温度由于无法及时放散而导致内部热量积聚，在温度梯度的作用下，引起轨道板上拱离缝等结构病害，加剧轨道结构累积变形和轮轨相互作用，严重地影响线路的安全性和平顺性。因此，研究外界环境与轨道板温度梯度本质联系，实现轨道板温度梯度状态的有效预警具有重要的理论和现实意义。目前，无砟轨道结构设计中所选取温度梯度多参考国内外相关铁路轨道结构、公路沥青路面和箱梁结构的正温度梯度经验公式来确定的。但在实际运营过程中，由于板式无砟轨道导热性能的差异，结构温度受气温、太阳辐射和风速影响较大，沿轨道板深度方向温度变化在时间上存在一定滞后，导致相关经验公式无法真实反映无砟轨道板温度梯度的实际分布。为修正此问题，并为后续结构设计和线路养护维修提供参考，国内外学者目前主要采用实测数据统计分析和数据趋势预测2种方法进行研究。前者是通过轨道板内布设传感器，对其温度状态进行长期监测，并对试验数据进行大样本的统计，研究结果表明：无砟轨道竖向正温度梯度与气温的日变化趋势大体相同，极端天气高温下会出现90 ℃/m以上的正温度梯度[2−3]，超过正温度梯度设计允许值[4]，导致板的翘曲变形急剧变大，服役性能大大降低。而后者同样利用现场实测数据，通过相关的预测算法如最小二乘法等进行样本的拟合逼近，从而预测出轨道结构温度和温度梯度，并建立特定条件下正温度梯度模式[5−7]。此外，闫斌等[8]基于日温差、日照时数和风速等气象因素实测数据对正温度梯度进行预测研究，通过BP神经网络方法，分析了轨道板竖向温度梯度的影响规律。上述两类方法虽较好地得到板内竖向正温度梯度，但需要在轨道板内部进行打孔安装相应的传感器，对结构体的完整性和耐久性产生重要影响，且所采用数据往往仅表征了相应测点的分布温度梯度分布规律；特别是当外界环境产生变化时，虽已有部分文献进行了研究，但其分析的温度范围较小，且未涉及正温度梯度设计允许值。因此，有必要结合相关实时气象参数数据，建立其与轨道板正温度梯度的分类预警模型，从而实现由外界气象参数即可对轨道温度梯度状态进行有效预判的目的。基于此，本文根据气象参量分布特征，利用支持向量机可以解决非线性问题、高维模式识别等优势，以轨道板正温度梯度为研究对象，将气温、太阳辐射以及风速作为模型的输入特征向量，构建基于气象资料的轨道温度梯度分类预警模型；通过实测数据进行模型的验证与相关参数优化，并给出相关指标阈值，从而提出轨道板温度梯度预警方法，为无砟轨道结构参数设计和养护维修方案的优化提供技术支撑和理论参考。

1 样本来源

本文选用华东地区某典型客运专线作为监测对象，线路运营速度为300 km/h，轨道结构为CRTSⅡ型板式无砟轨道，线路基础形式为路基。通过在现场安装PT100型温度传感器和气象站进行轨道板板表/板底温度(℃)以及气温(℃)，太阳辐射(W/m2)和风速(m/s)等气象参数的数据采集。采样频率为次/30 min，测试共计获取了888组数据。

若轨道板竖向正温度梯度为：

其中：为温度梯度，℃/m；T和T分别为轨道板板表和板底温度，℃；Δ为轨道板板表与板底之间的距离，cm。

将实测轨道板温度数据代入式(1)，得到正温度梯度范围为0.29~111.66 ℃/m。另外，据研究表明[1]，气温、太阳辐射量，风速往往是影响轨道板竖向温度梯度的最主要的因素。因此，结合上述3个参量以及计算出的竖向温度梯度，其分布如图2所示。此外，由于现行轨道状态评价体系中尚未涉及轨道板正温度梯度的评价与预警，因此，这里参考相关设计规范[5]中给出的结构设计最大允许值90 ℃/m作为后面分析评价指标值。

图1 气象参数分布规律图

由图1可知，温度梯度、气温、太阳辐射量及风速峰值分别可达111.66 ℃/m，40.8 ℃，1 091 W/m2和5.0 m/s。检测结果中，已有近8%的数据超过了规范设计的正温度梯度。这说明在极端的气温下，轨道板端将会引起超过结构安全允许度的变形，造成轨道板上拱、离缝等病害，成为高铁安全营运的严重隐患，因此，需要加强对轨道板温度梯度状态的预警。

对比气象因素分布可知，轨道板正温度梯度与气温、太阳辐射、风速之间具有较强的关联性，即气温或太阳辐射量越大、风速相对不变时，正温度梯度越易于超过设计允许值；风速较小而气温和太阳辐射量相对不变时，轨道板正温度梯度则相对较大。而对比气象参数与正温度梯度分布规律可以发现，两者之间具有一定的随机性和非线性特征即两者存在着较强的非线性映射关系。

2 轨道板正温度梯度的支持向量机分类预警模型

2.1 支持向量机

支持向量机(Support Vector Machine, SVM)是一种通过寻求结构化风险最小来提高学习机泛化能力，实现经验风险和置信范围的最小化的分类算法，适用于结构状态的预警分类分析[9−10]。

如图1所示，由于轨道板正温度梯度和气象参数之间为线性不可分，因此，需要先将支持向量分类模型通过非线性变换将输入空间映射到一个高维特征空间，然后在这个新空间中求取最优线性分离超平面对正温度梯度分类，而这种非线性变换是通过定义适当的核函数来实现的，输出是由核函数内积运算的线性组合得到，算法流程如图2所示。

在上述求解过程中，需要采用不同的核函数及其参数构造空间中不同类型的非线性决策的学习机，进而寻找出气象参数分布特点与最优超平面之间对应关系，实现对正温度梯度进行有效分类，并以识别准确率作为指标对模型进行评价。

2.2 模型建立

为了建立有效的支持向量机分类预警模型以满足实际需求，本文主要从样本选择方式、核函数选取及参数优化等关键点进行分析，流程如图3 所示。

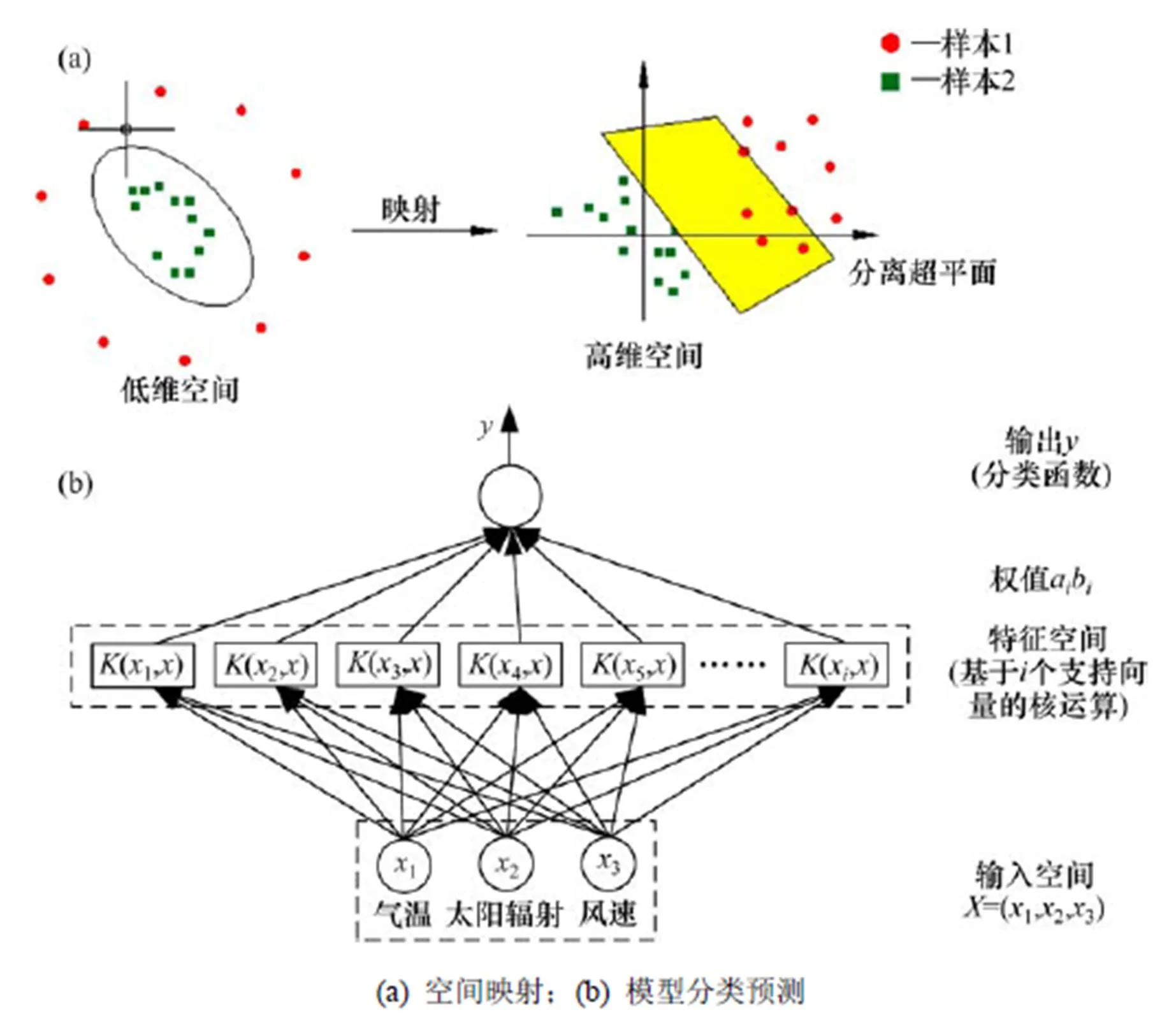
图2 SVM流程示意图

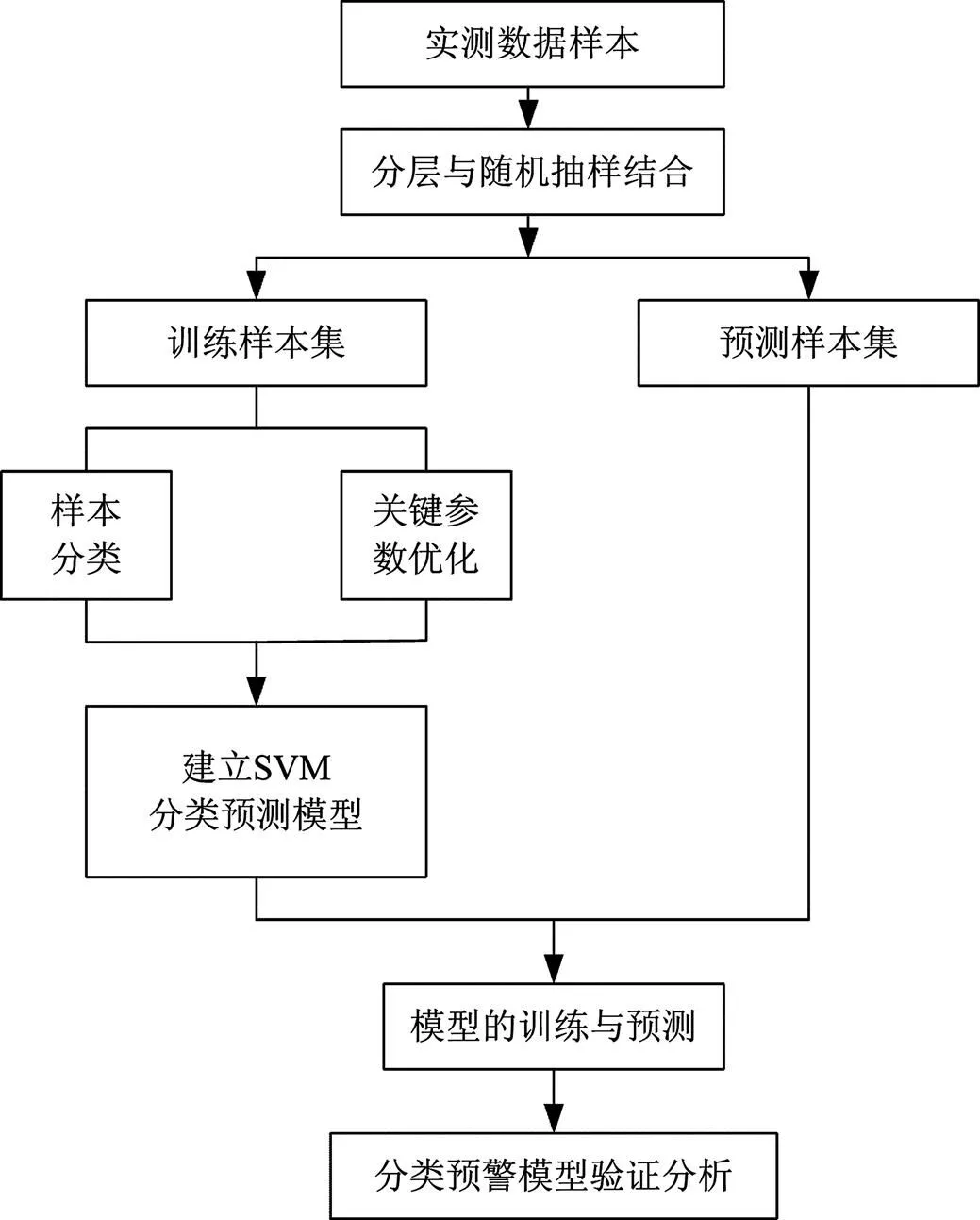
图3 SVM预警模型流程图

2.2.1 样本选择方式

将实测888组数据中轨道板正温度梯度值未超过90℃/m的样本作为1类样本，轨道板正温度梯度值超过90℃/m的样本作为2类样本。此外，为了保证1类样本与2类样本都能涵盖不同分类信息，对样本分层抽样以提高模型识别精度随机选取1类样本75%与2类样本75%作为训练样本集，剩余的25%的1类样本与25%的2类样本作为预测样本集，如图4所示。

2.2.2 核函数选取及其参数优化

鉴于气象参数与轨道板正温度梯度的非线性映射关系，在分类与识别过程中难以处理，而核函数作为支持向量机分类预警模型建立的核心之一，不仅可以解决维数灾难的问题，而且能够在没有增加计算复杂度的基础上，使得特征空间中的气象参数变得线性可分，进而对正温度梯度进行有效分类。核参数和惩罚因子，反映了气象参数的分布特点或范围特性，其改变实际上改变了样本子空间分布的复杂程度，是保证建立的正温度梯度分类预警模型是否具有良好推广性的重要保障。因此，核函数选取及其参数优化过程是能否得到气象参数与正温度梯度非线性映射关系的关键，具体过程如图5所示。

图4 样本选择方式

图5 核函数选取与参数优化

考虑到SVM在实际应用中核函数种类不多，为了得到较好的气象参数与轨道板正温度梯度的映射关系，分别采用4种核函数：线性核函数，多项式核函数，高斯核函数以及Sigmoid核函数构造分类模型，相同样本、固定参数下不同核函数的对比结果如表1所示。

表1 核函数对比

相较于其他核函数，高斯核函数在识别准确率以及计算效率上都有着较为明显的优势，准确率更是高达98.192 8%，更适合用于轨道板正温度梯度预警模型。

在以高斯核函数为核函数的支持向量机分类模型中，需要确定核参数()和惩罚因子2项参数，但关于其相关的选取，目前尚无公认统一的方法。因此，本文通过将训练集作为原始数据，利用K-CV的方法得到最高识别准确率下最佳()和。当出现多组()和对应最高识别准确率时，为避免过高的导致过学习状态，选取最小的那组()和作为最佳参数。参考相关文献和试运算经 验[11−12]，在寻优过程中将和的取值范围分别设定为[2−10, 210]和[2−10, 210]，步进都为1；10折交叉验证结果如图6所示。

图6 参数优化

由图6可知，等高线图中轴表示取以2为底对数后的值，轴表示(图中表示)以2为底对数后的值，最优惩罚系数值=32，最优核参数值=2，最高平均识别准确率为98.8%。

2.3 模型验证

为了验证所提方法的有效性和准确性，这里将预测样本集所对应的气象参数输入到已建立的SVM分类预警模型中，预测轨道板正温度梯度是否超过结构设计最大允许值90℃/m，预测结果与实测结果对比如图7所示。

图7 预测结果与实际结果对比图

由图7可以看出，预测结果采用○表示，实际结果采用※表示，若预测结果与实际结果一致，则2个符号重合，若预测结果与实际结果不一致，则2个符号则对应轴出现在不同的轴上，图9和图10也根据此规律表示。

所得预测样本集中除3个样本的预测结果与实际结果出现偏差(包括1个过度识别，2个未识别出超过正温度梯度设计允许值。)，其余均正确反映了轨道板正温度梯度的分类状态，所得到预警分析准确率为98.648 6%。因此，本文所提的支持向量机分类预警模型可通过气象参数有效地识别轨道板正温度梯度分类状态，满足列车运营期间对轨道板内正温度梯度预警的要求。

3 气象参数预警指标的确定

气象学上将日最高气温达到或超过35 ℃时称为高温，若连续3 d最高气温在35 ℃以上，则达到高温黄色预警标准。但对于高速铁路无砟轨道结构而言，仅参照气象学角度的高温定义尚不够具体充分，尚需要根据轨道板正温度梯度实际服役状态，确定相应的分类预警标准。

3.1 预警指标值的选取

对于高速铁路无砟轨道结构而言，由现场实测可知，有必要对气温在35 ℃附近的轨道内部温度分布进行研究[13]；而太阳辐射量和风速同样作为影响轨道板内部温度分布的重要因素，需要对相关参数的预警指标量值进行确定。

本文利用既有极端高温下的气象参数资料，采用前文中SVM分类预警模型，对轨道板正温度梯度分类预警状态进行分析，预测数据共有222组，包含随机抽样1类样本204组，2类样本18组，约占各类数据总样本的25%；其结果与气象参数联合分布如图8所示。

图8 预测结果与气象参数联合分布图

由图中气温−太阳辐射投影面可知，气温和太阳辐射量对正温度梯度梯度具有较为明显地对应关系，当气温超过33.9 ℃且太阳辐射量超过733 W/m2时，正温度梯度往往呈现超过设计允许值90 ℃/m；对风速而言，其对正温度梯度影响无显著规律，轨道板正温度梯度超限则集中于2 m/s以下的区段。因此，综合相关的历史气象资料分析结果，本文可以初步将气温大于或等于33.9 ℃、太阳辐射量大于或等于733 W/m2量值以及瞬态参量风速在小于或等于2 m/s 3个指标选为轨道板正温度梯度SVM分类预警模型的指标值。为了进一步验证预警指标的可信度，本文还将对指标进行分情况讨论。

3.2 指标值的验证

为了验证所提预警指标的准确性，这里采用本文所提SVM分类预警模型方法进行分析，比较分析预测结果和实测结果。

3.2.1 气温与太阳辐射

将222组预测样本集的预测结果与实际结果对比，分别对正温度梯度所对应的气温、太阳辐射的预警指标进行分析，建立气象参数-类别图。如图9所示。

由图9可知，对于正温度梯度超过设计允许值的情况，气温与太阳辐射量有明显的集中趋势。在预测样本集中，当太阳辐射量大于或等于733 W/m2，共有45个样本；当温度大于或等于33.9 ℃，共有56个样本；同时满足上述2个条件的样本共有24个；都包含3个错误信息，识别准确率为87.5%，其中1个为过度识别，2个为未识别，主要是由以下2个原因引起该误差，一方面通过分析前一时刻或下一时刻可知，主要是由于风速出现了骤变，导致正温度梯度短时间内发生变化。另一方面，由于数据有限，模型训练时不能完全考虑特殊情况下的温度梯度变化情况。但考虑到建立的分类模型是为预警提供依据，可允许少量过度识别的特殊性。因此，以温度大于或等于33.9 ℃和太阳辐射量大于或等于733 W/m2为正温度梯度的预警指标，该模型可保证91.67%识别准确率。

3.2.2 风速

在以太阳辐射量大于或等于733 W/m2，温度大于或等于33.9 ℃为预警指标可有效满足实际需求的基础上，进一步研究风速对正温度梯度的影响，通过筛选后的24个样本建立风速-类别结果对比图观察其分布情况，如图10所示。

图9 气象参数-类别散点图

图10 风速-类别

上述对气温与太阳辐射量筛选后的24个样本中，共有3个样本识别错误，未识别错误有2个且都分布在2.2 m/s以上。因此，以太阳辐射量大于或等于733 W/m2，温度大于或等于33.9 ℃，风速小于或等于2 m/s为正温度梯度的预警指标，其识别准确率为96%。比之前具有显著提高，并且只存在一个过度识别错误，可以满足正温度梯度预警的目的。

4 结论

1) 轨道板正温度梯度分类预警模型可采用支持向量机方法建立，且利用高斯核函数、10折交叉验证的方法可实现参数优化，所建立模型分类预警识别率为98.648 6%。可有效地识别轨道板竖向正温度梯度状态，满足列车运营期间对轨道板内正温度梯度预警的要求。

2) 根据统计资料与现场实测，给出了轨道板正温度的预警指标值为太阳辐射量大于或等于733 W/m2，温度大于或等于33.9 ℃，风速小于或等于2 m/s，并保证在此指标下预警具有96%的可靠性，为轨道结构的设计改进、病害预防以及养护维修提供方向性指导与科学的建议。

3) 本文只针对华东地区无砟轨道竖向正温度梯度进行研究，鉴于我国幅员辽阔，各个地区气象参数对轨道板正温度梯度影响均不同，因此有必要针对不同地区提出不同的指标，实现对轨道服役状态分类预警。

[1] 欧祖敏, 孙璐, 程群群. 基于气象资料的无砟轨道温度场计算与分析[J]. 铁道学报, 2014(11): 106−112. OU Zumin, SUN Lu, CHENG Qunqun. Analysis on temperature field of ballastless track structure based on meteorological data[J]. Journal of the China Railway Society, 2014(11): 106−112.

[2] 赵坪锐, 刘学毅, 杨荣山, 等. 双块式无砟轨道温度荷载取值方法的试验研究[J]. 铁道学报, 2016(1): 92−97. ZHAO Pingrui, LIU Xueyi, YANG Rongshan, et al. Experimental study of temperature load determination of bi-block ballastless track[J]. Journal of the China Railway Society, 2016(1): 92−97.

[3] 尤明熙, 高亮, 赵国堂, 等. 板式无砟轨道温度场和温度梯度监测试验分析[J]. 铁道建筑, 2016(5): 1−5, 9. YOU Mingxi, GAO Liang, ZHAO Guotang, et al. Analysis of monitoring test for slab-type ballastless track temperature field and temperature gradient[J]. Railway Engineering, 2016(5): 1−5, 9.

[4] TB10621—2014, 高速铁路设计规范[S]. TB10621—2014, Code for design of high speed railway[S].

[5] 吴斌, 刘参, 曾志平, 等. CRTSⅡ型板式无砟轨道温度场特征研究[J]. 铁道工程学报, 2016(3): 29−33. WU Bin, LIU Can, ZENG Zhiping, et al. Research on the temperature field characteristic of CRTSⅡ slab ballastless track[J]. Journal of Railway Engineering society, 2016(3): 29−33.

[6] 赵坪锐, 邓非凡, 丁晨旭, 等. 基于统计分析方法的成都地区无砟轨道温度梯度预测[J]. 铁道建筑, 2016(5): 43−46. ZHAO Pingrui, DENG Feifan, DING Chenxu, et al. Temperature gradient prediction of ballastless track in chengdu region based on statistical analysis method[J]. Railway Engineering, 2016(5): 43−46.

[7] 戴公连, 苏海霆, 闫斌. 圆曲线段无砟轨道横竖向温度梯度研究[J]. 铁道工程学报, 2014(9): 40−45. DAI Gonglian, SU Haiting, YAN Bin. Study on horizontal and vertical temperature gradient of ballastless track on curve line[J]. Journal of Railway Engineering Society, 2014(9): 40−45.

[8] 闫斌, 戴公连, 苏海霆. 基于气象参数的轨道板竖向温度梯度预测模型[J]. 华南理工大学学报(自然科学版), 2014(12): 9−13. YAN Bin, DAI Gonglian, SU Haiting. A meteorological parameters-based prediction model of vertical temperature gradient of track plate[J]. Journal of South China University of Technology (Natural Science Edition), 2014(12): 9−13.

[9] Cristianini N, Shawe_Taylor J. An introduction to support vector machines and other kernel-based learning methods[M]. Cambridge: Cambridge University Press, 2000.

[10] Hasitic T, Tibshirani R, Fruedman J. The elements of statistical learning, data mining, inference, and prediction [J]. The Mathematical Tatelligencer, 2005, 27(2): 83−85.

[11] Mitra V, Wang C, Banerjee S. Text classification: a least square support machine approach[J]. Applied Soft Computing, 2017, 7(3): 908−914.

[12] Varewyck M, Martens J P. A practical approach to model selection of Gaussian support vector machine[J]. IEEE Transaction on Systems, Man, and Cybernetics, Part B (Cybernetics), 2009, 39(5): 1292−1307.

[13] 何元庆. 华东地区CRTSⅡ型板式无砟轨道温度特性试验分析[J]. 铁道建筑, 2017(3): 102−105. HE Yuanqing. Experimental analysis on temperature characteristics of CRTSⅡ ballastless track in East China[J]. Railway Engineering, 2017(3): 102−105.

(编辑 蒋学东)

A novel method of fore-warning the positive temperature gradient of CRTS Ⅱ ballastless track based on support vector machine

GUO Yunqi1, LI Zaiwei1, 2, 3, HE Yuelei1, LU Hongyao1

(1. School of Urban Rail Transportation, Shanghai University of Engineering Science, Shanghai 201620, China; 2. Engineering Research Center of Railway Environmental Vibration and Noise of Ministry of Education, East China Jiaotong University; Nanchang 330013, China; 3. School of Civil Engineering and Architecture, Beijing Jiaotong University, Beijing 100044, China)

The temperature gradient of ballastless track is not only the important characteristic of the track structure under the temperature load, but also the key parameter of structural design and maintenance. Aiming at the issue of temperature gradient monitoring and warning of track slab, based on the real-time measurement of data samples of the operating line, the meteorological parameters such as temperature, solar radiation and wind speed were used as the representative input parameters, and the positive temperature gradient of the track slab as the output parameter. The fore-warning model of track temperature gradient classification was established based on the support vector machine, and the selection method of key parameters of the model was given; The effectiveness and accuracy of the fore-warning model were verified by the actual measured data and the warning threshold of the meteorological parameters was determined by combining the historical meteorological data and using the established model. The results show that the accuracy of the positive temperature gradient warning model was 98.6486%. The warning indices of air temperature, solar radiation and wind speed were 33.9 ℃, 733 W/m2and 2 m/s, respectively, and the reliability was 96%, which could provide guidance and reference for the design improvement, distress prevention and maintenance of the track structure.

high speed railway; ballastless track; temperature gradient; support vector machine; classification and fore-warning

10.19713/j.cnki.43−1423/u.2018.09.004

U213.2

A

1672 − 7029(2018)09 − 2209 − 08

2017−08−14

国家自然科学基金资助项目(51478258)；上海市科委重点支撑资助项目(16030501400)

李再帏(1983−)，男，吉林大安人，副教授，博士，从事轨道结构振动研究；E−mail：lzw_5220964@163.com