直线游标永磁电机反步滑模控制研究

唐红雨，徐 峰，黄海峰

(镇江市高等专科学校，镇江 212003)

0 引 言

轨道交通作为解决人们出行的一种新型交通工具受到了广泛的关注，而电机作为轨道交通驱动系统的核心部件得到了广泛的研究[1-2]。旋转电机必须通过变速传动系统才能把动力传递给机车，而直线永磁电机则可以省略传动机构，无需转换装置，就可以把电能转换成直线运动机械能[3-4]。普通直线永磁电机需要将永磁体或绕组沿轨道全线铺设，成本很高；直线初级型永磁电机由于将绕组与永磁体同时放置在初级上，次级仅需将导磁材料开槽形成齿槽结构，因而能够节省材料，降低工程成本。直线游标永磁电机(以下简称LVPM电机)[5]是一种新型的特种电机，在直线初级永磁电机基础上发展而来，利用磁通切换原理工作，区别仅在于定子齿端不是一对永磁体而是若干对永磁体[6]。该电机能够在低速时利用自身的游标效应产生较大的推力，因而在船舶推进、轨道交通等领域得到较为广泛的应用[7-8]。LVPM电机系统是多变量、强耦合、非线性的复杂系统，传统的比例积分微分控制性能不佳，滑模控制无需被控对象的精确数学模型，抗干扰能力强，鲁棒性好等优点，在电机控制领域与智能方法相结合而被广泛采用[9-11]。

本文采用反步控制理论与滑模控制相结合的方法，设计中间虚拟控制量来实现LVPM电机的位移控制器，通过最小参数学习算法逼近未知项[12]，获得系统的最佳状态，提高LVPM电机控制动静态性能。

1 LVPM电机模型

本文的研究对象是采用组合永磁体阵列的新型初级LVPM电机，该电机的次级相当于传统转子永磁型电机的定子，初级相当于传统转子永磁型电机的转子，也叫动子，横截面如图1所示。

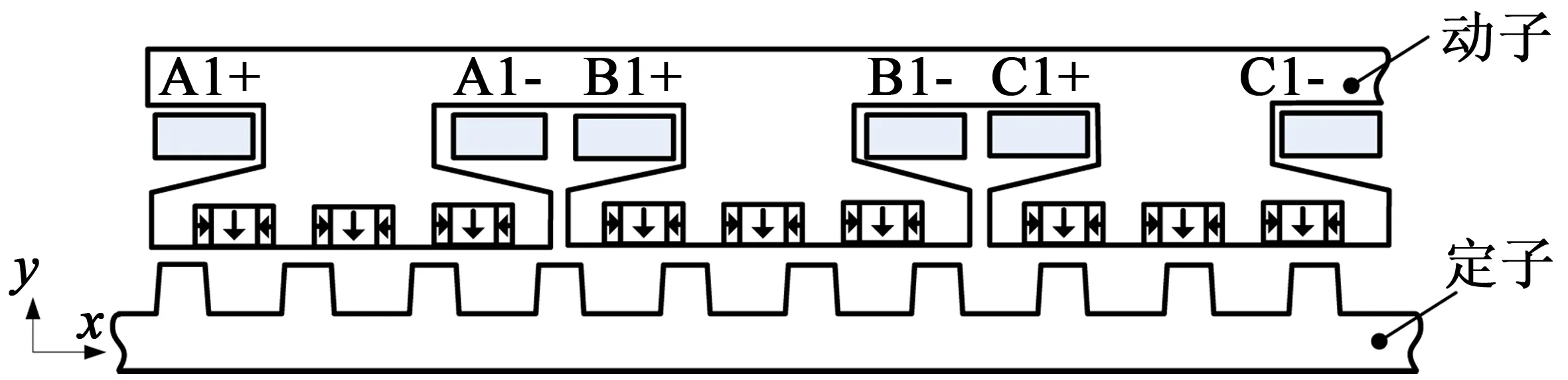
图1 LVPM电机横截面

参照旋转坐标系，把次级坐标系当作定子坐标系，初级坐标系当作转子坐标系[12]。LVPM电机在d，q轴下的电压方程可以写成[13-14]：

(1)

式中：ψd=Ldid+ψf；ψq=Lqiq。如果忽略电阻，则LVPM电机的推力方程可以写成：

(2)

式(2)的第一部分为永磁磁链与q轴电流产生的，它与电机的角频率和速度有关；第二部分为d轴跟q轴电感不相等引起的推力，如果设计时采用隐极机形式，则此部分不存在，另外，id=0控制策略也可以消除此部分产生的力；第三部分是由d轴跟q轴之间的互感产生的推力，通常情况下，互感都比较小，因而此部分力被忽略掉。角速度ωe=pπυ/τ，并且采用id=0控制策略，则：

(3)

LVPM电机机械运动方程：

(4)

式中：ud，uq为d，q轴电压；id,iq为d，q轴电流；R为每相绕组电阻；p为极对数；τ为极距；ψf为永磁体磁链；Ld为直轴励磁电感；Lq为交轴励磁电感；υ为动子线速度；ωr为动子机械角速度；ωe为动子电气角速度；Fl为直线电机的负载阻力和电机本身的定位力之和；Bv为粘滞摩擦系数；M为动子总质量。

2 反步滑模控制器设计

LVPM电机控制系统框图如图2所示。控制系统电流控制器采用常规的PI控制，采用光栅尺采集位置信息，位置控制器采用反步滑模控制方案，位置控制器的输入为位置跟踪误差和速度跟踪误差，输出控制量为q轴电流。

图2 LVPM电机控制系统框图

LVPM电机在动力传动过程中，存在一些不确定因素影响控制过程。滑模控制鲁棒性强，对系统参数摄动具有不变性，但存在滑模抖振；反步法是一种倒推式设计方法，能够将复杂非线性系统分解成不超过系统阶数的子系统，再为每个子系统设计部分Lyapunov函数和中间虚拟控制量，然后将它们集成起来完成整个控制律的设计[15-16]。把反步法和滑模控制结合，能弥补常规PID控制和滑模控制的不足。根据LVPM电机的数学模型来设计其滑模控制器，设υ*为给定速度，υ为实际速度，s为动子位移，s*为位移期望值，取u=iq，则:

(5)

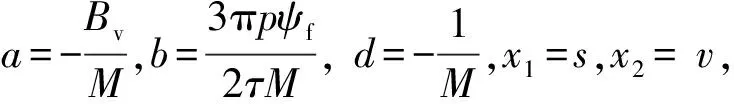
(6)

在实际LVPM电机运行中，不确定项存在一些变化，状态方程改写成：

(7)

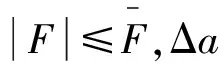
(8)

反步滑模控制器设计分为两步。

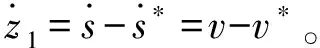
γ=ηz1+z2

(9)

式中：η>0。为降低滑模阶数和计算的复杂性，这里选择一阶线性滑模函数。

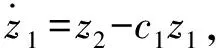
(10)

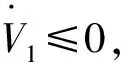
设计控制器：

u=b-1{-η(z2-c1z1)-a(z2+s*-c1z1)-

(12)

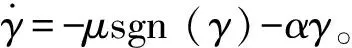
将式(12)代入式(11)得：

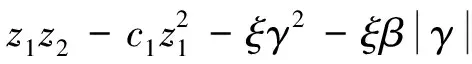
(13)

式(13)中，F为不确定项，是未知非线性函数，采用神经网络对不确定项F进行自适应逼近[17]，逼近算法：

(14)

F=WTh(x)+ε

(15)

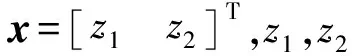
(16)

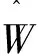
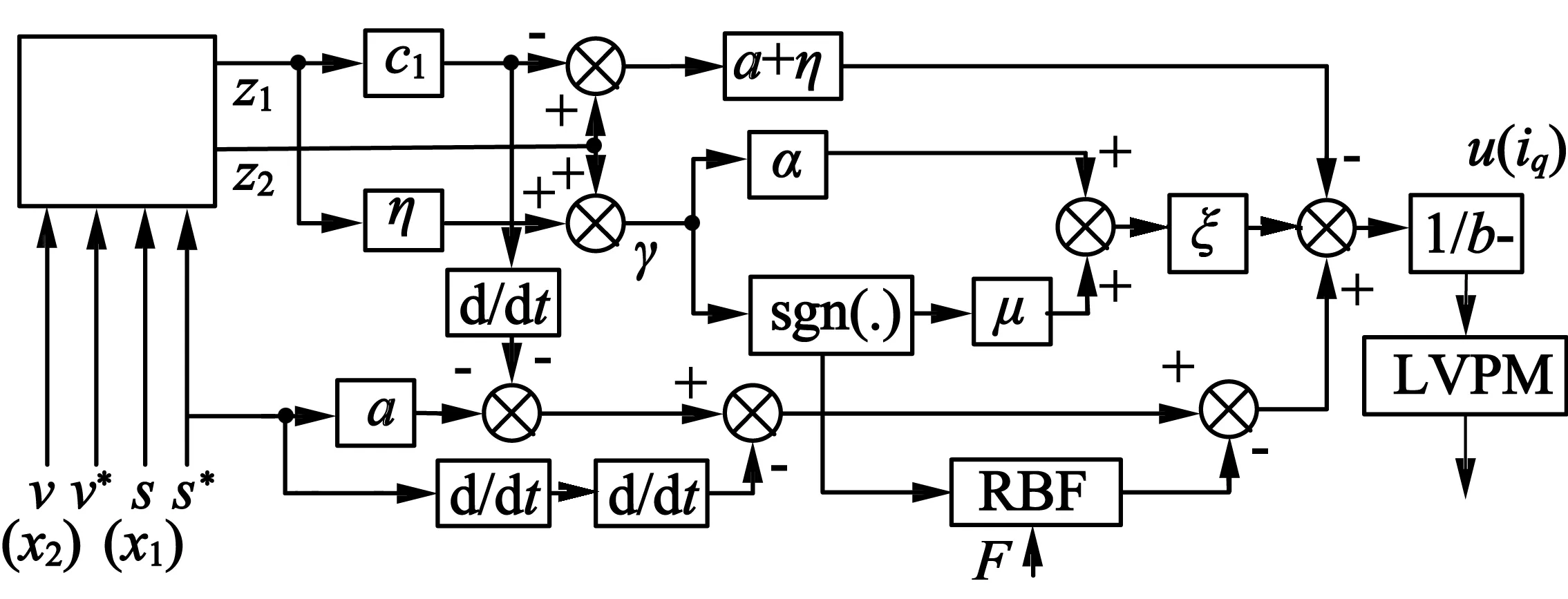
图3 反步滑模控制器框图

3 仿真与实验

为验证LVPM电机反步滑模控制策略的有效性，搭建了仿真模型。LVPM电机参数如下：绕组电阻R=2.5 Ω，极对数p=1，极距τ=0.02 m，永磁体磁链ψf=0.25 Wb，d,q轴电感Ld=Lq=0.024 5 H，粘滞摩擦系数Bv=0.2 N·s·m-1，动子质量Mr=3.5 kg，电流环kp=200，ki=5，速度环kp=300，ki=150，动子载物质量Ml=3.0 kg，负载推力初始为Fl=120 N。

图4为输入阶跃信号，给定速度指令v*=1m/s时的速度和推力仿真图。可以看出，相比传统 PID控制，反步滑模控制方法的响应时间略有加快，且超调量明显下降，从10%降为2%，在阶跃响应瞬间，推力明显突变，但本方法要好于PID控制方法，说明系统在动态和快速性方面都得到较大的提高。

(a) 速度响应

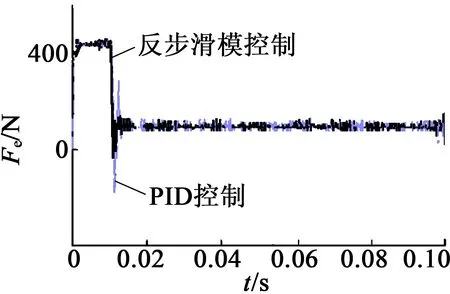
(b) 推力响应

图5为在0.5 s速度从1 m/s降为0.8 m/s的响应图，图6为在0.06s推力从120N升为200N的响应图。从速度对比图中看出，PID控制在系统转速变化时有较大的波动，超调量比本方法大8%，响应速度慢一些。从推力对比图中可以看出，在速度受到干扰突变时，反步滑模控制器控制方法的速度脉动更小，说明此方法对系统扰动具有较好的抑制性能。从推力响应曲线可以看出，与PID方法相比，本方法响应速度更快，因而，本方法比PID控制方法具有更好的控制性能。

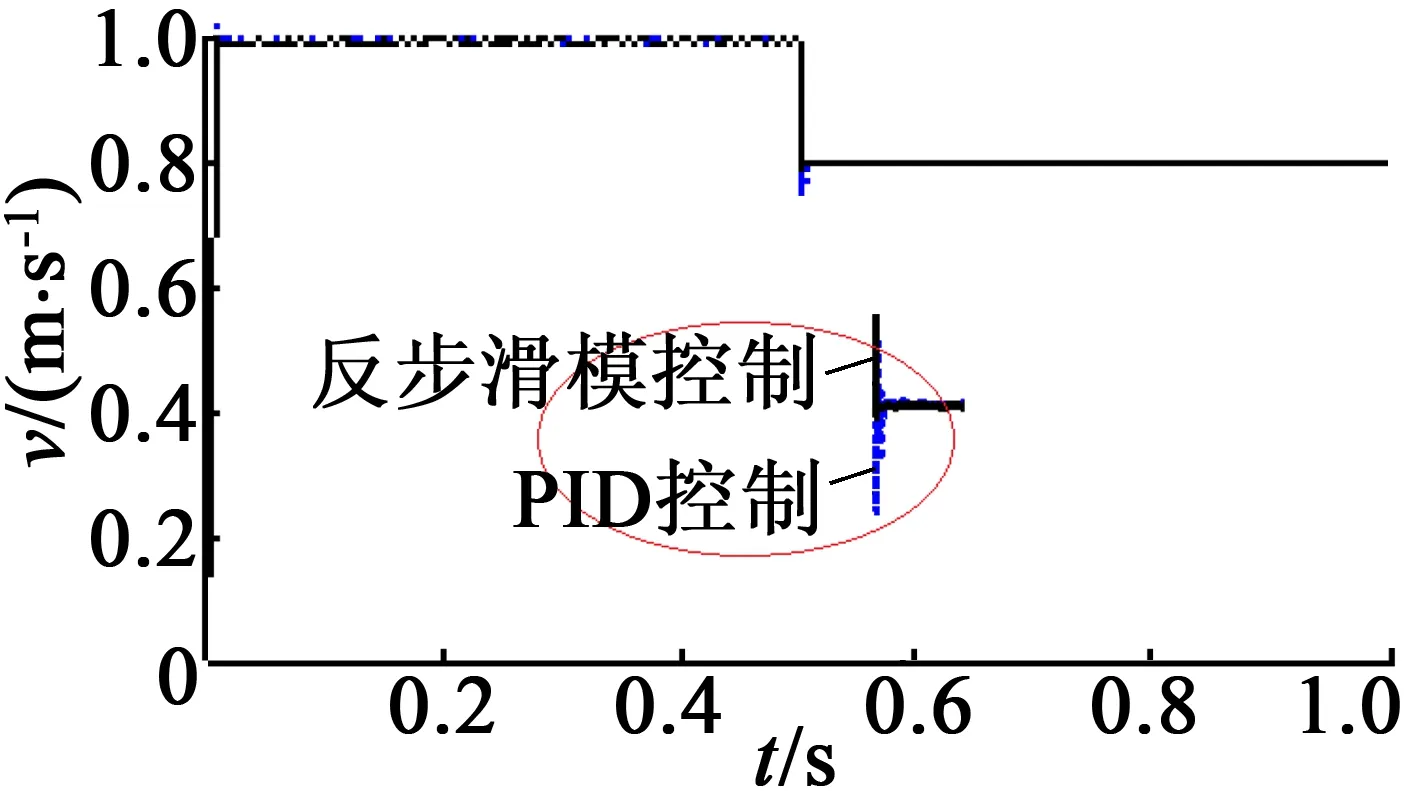
(a) 速度响应

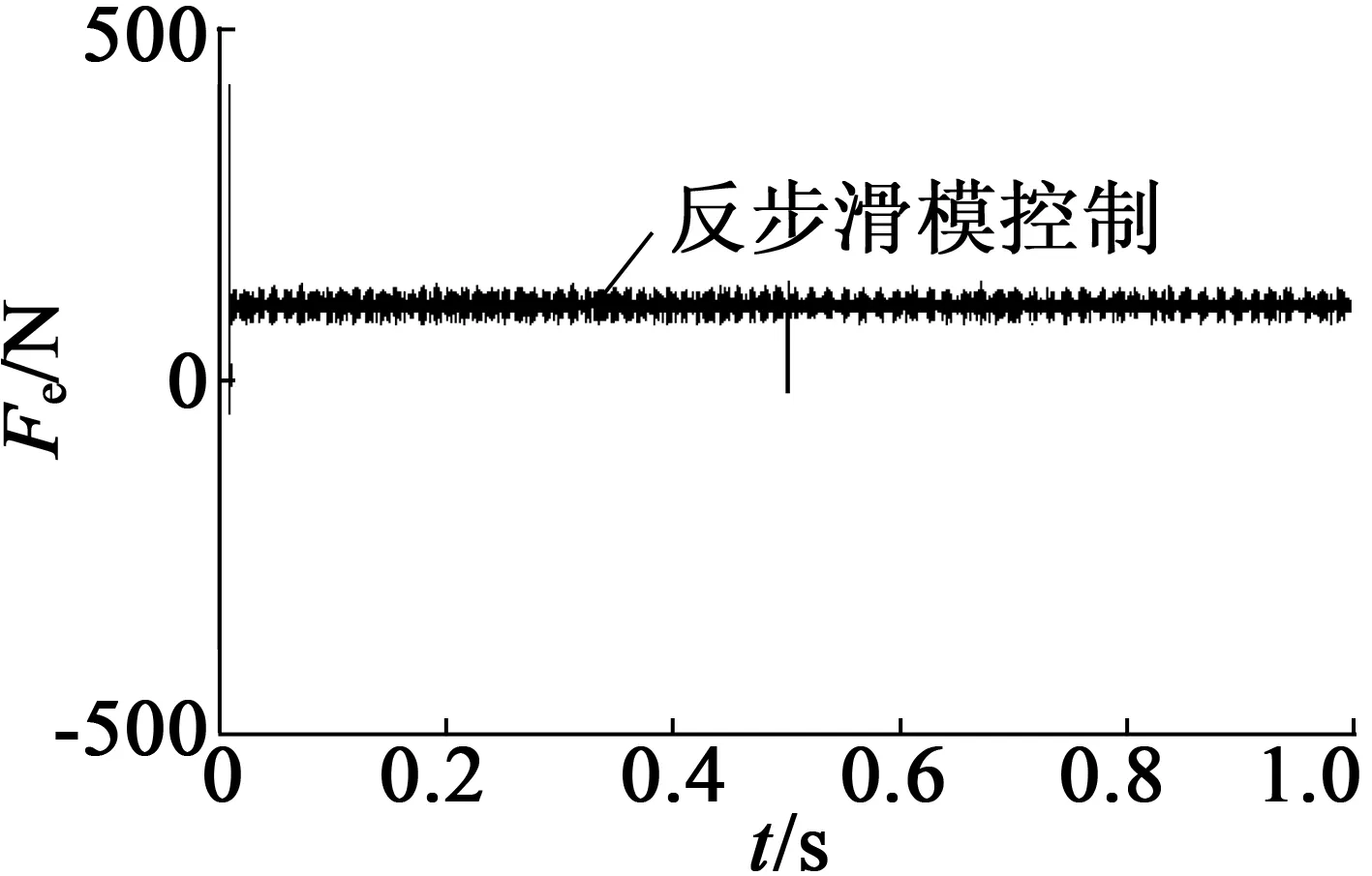
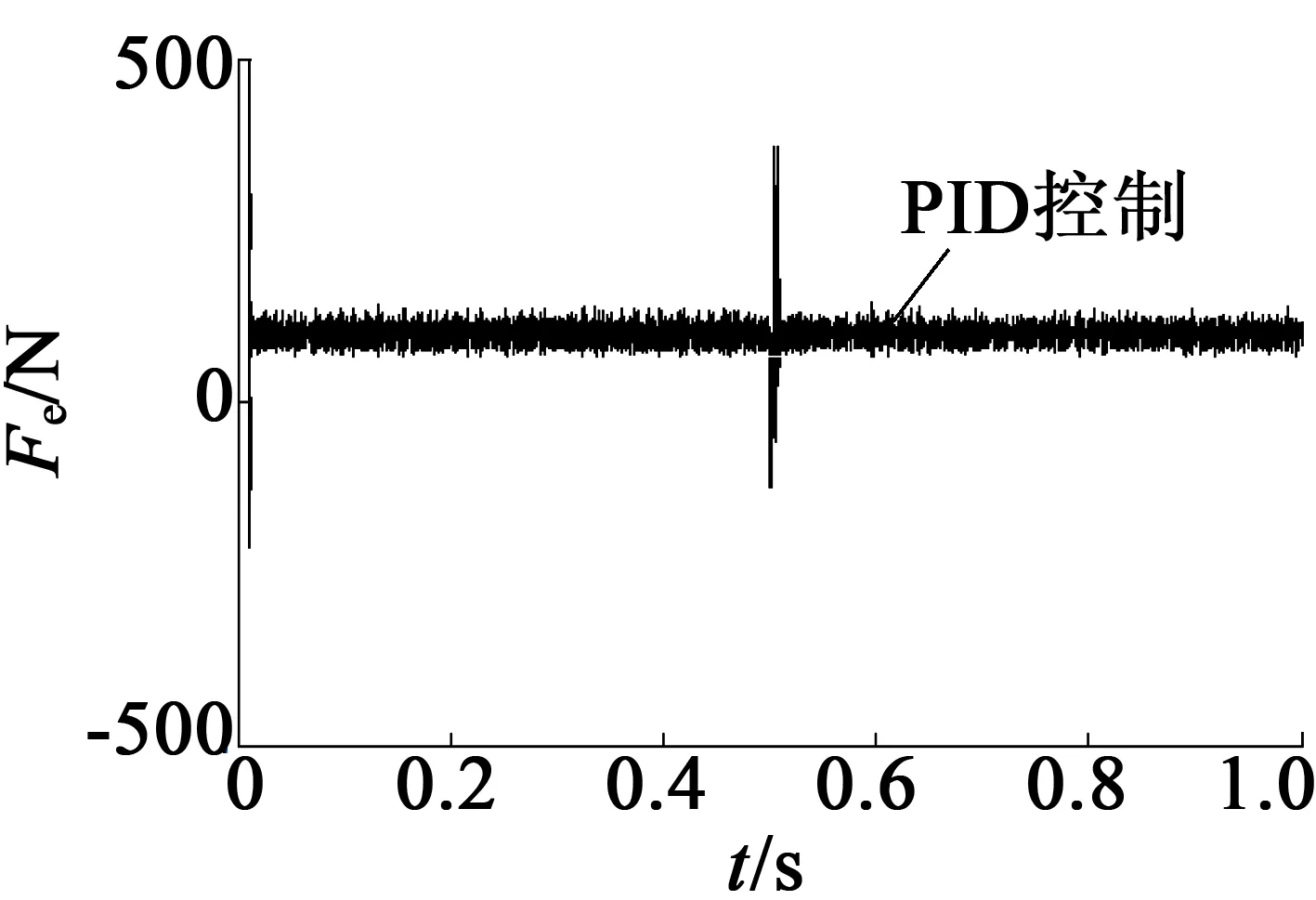
(b) 推力响应

(a) 速度响应

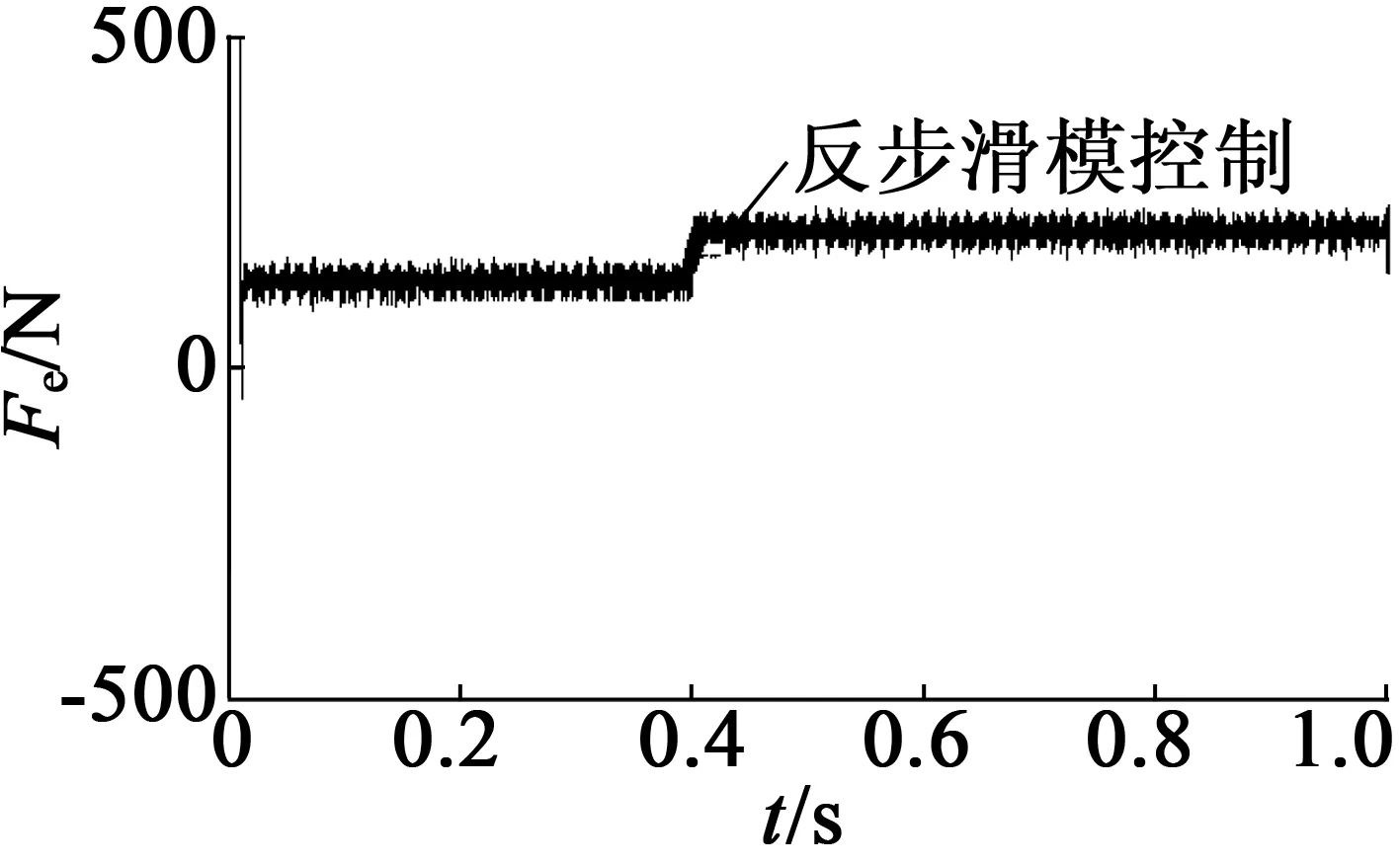
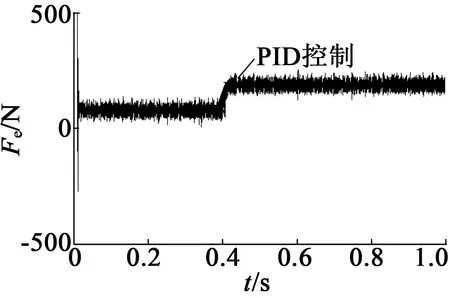
(b) 推力响应

为了进一步验证本方法的可行性，在实验室搭建了LVPM电机实验平台，LVPM电机驱动控制系统实物图如图7所示，主要包括LVPM电机、智能功率驱动模块、DSP 控制模块、电源模块、仿真器、光栅检测传感器等。

图7 实验平台

给定线速度为0.3 m/s，LVPM电机响应如图8所示，由于推力无法直接测量，以q轴电流代替。

(a) PID控制

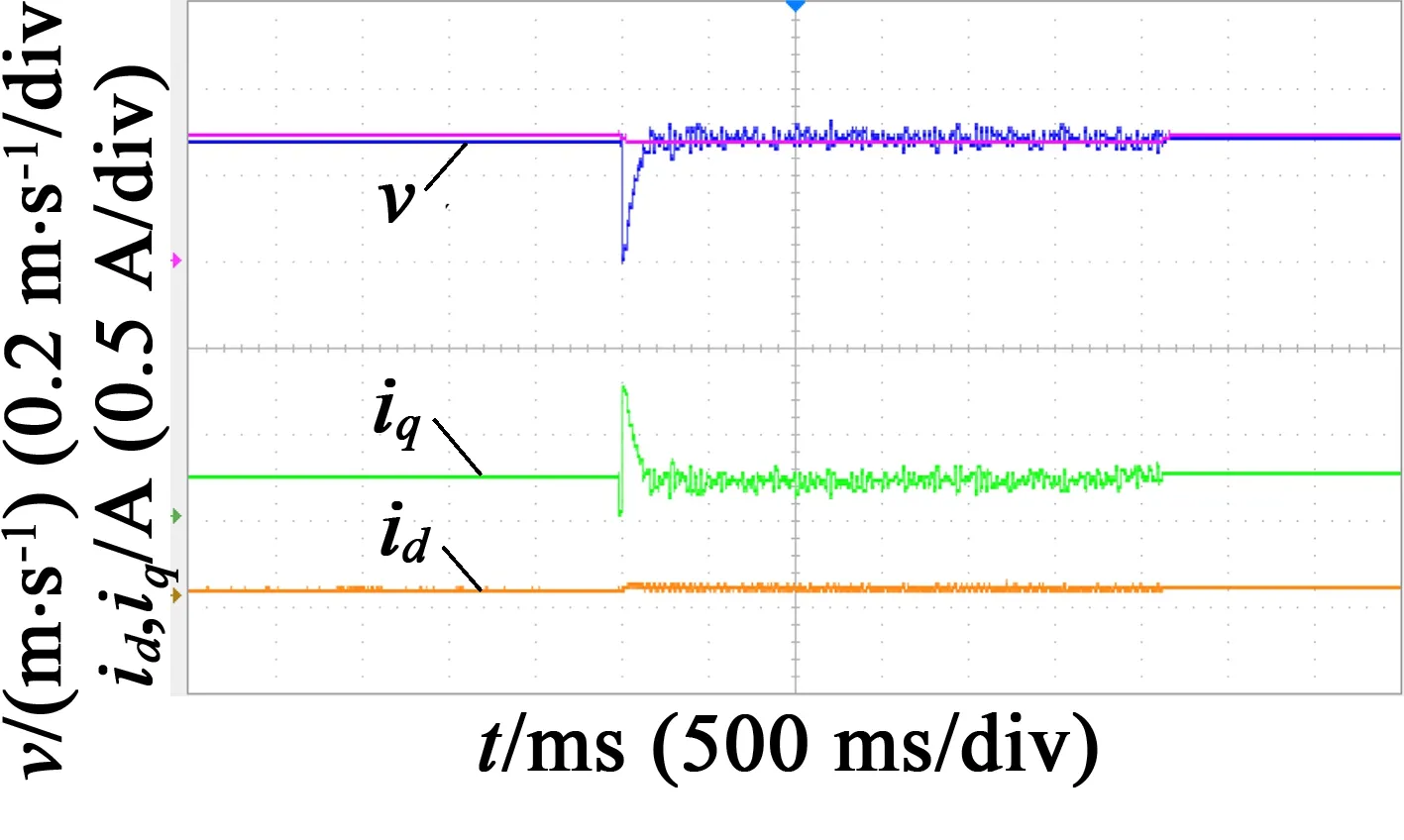
(b) 反步滑模控制

从图8可以看出，反步滑模控制方法在速度响应、电流id，iq响应上比PID控制方法平稳，虽然电流iq在响应瞬间波动大一些，但稳态后的脉动明显小于PID控制方法，且速度响应快速性提高了，超调很小。所以，本方法在提高LVPM电机性能上优于PID控制方法。

4 结 语

本文将反步控制和滑模控制相结合，设计反步滑模控制器，采用最小参数学习算法逼近未知干扰项，该方法应用于LVPM电机速度环控制，使滑模变量在有限时间内收敛到零，提高了LVPM电机系统的静态与动态性能。结果表明，所设计的控制器减少了系统的抖振，保证了LVPM电机系统的位置跟踪能力和鲁棒性，提高了系统动态性能。