活性粉末混凝土动静弹性模量试验研究

方 志, 周传波

(湖南大学 土木工程学院, 湖南 长沙 410082)

活性粉末混凝土RPC(Reactive Powder Concrete)是一种以水泥、矿物掺合料、细骨料、高强度微细钢纤维或有机合成纤维等原料生产的超高性能纤维增强细骨料混凝土[1]，于1993年由法国BOUYGUES公司率先研制成功[2]。与普通混凝土相比，RPC强度高、韧性强和耐久性好，因而被称为超高性能混凝土，具备良好的工程应用前景[2-3]。弹性模量是RPC的基本力学性能参数之一，目前主要采用静力法进行测试[4]。但静力法存在测试费时、操作复杂、试验设备要求高及在原位取样测试时还对结构造成损伤等不足。超声脉冲法和冲击回波法具有快捷、简便、无损的特点，已被用于普通混凝土的弹性模量测试[5-7]。RPC较普通混凝土材质更加均匀，因而更适合采用超声脉冲法或冲击回波法进行弹性模量测试，但目前国内外对采用这两种方法进行RPC弹性模量测试的研究较少，鲜有建立其动弹性模量和静弹性模量间的定量关系。

Bungey[5]采用超声脉冲法测定了普通混凝土的弹性模量及泊松比；吕小彬[6]采用冲击回波法对不同尺寸普通混凝土试件的弹性模量进行测试，得到弹性模量随试件尺寸的变化规律；文献[7]认为普通混凝土的静弹性模量可取为冲击回波法所测动弹性模量0.8倍。Washer[8]采用超声脉冲法测试了RPC立方体试件的弹性模量，得到了动弹性模量大于静弹性模量的结论，但因试件样本太少，并未得到动、静弹性模量间的定量关系，且没有明确钢纤维掺量和强度等级对波速及弹性模量的影响规律。

基于此，本文分别采用静力法、超声脉冲法和冲击回波法对不同强度等级和不同钢纤维掺量RPC的弹性模量进行测试，以期获得动、静弹性模量间的定量关系，并明确钢纤维掺量对RPC抗压强度、波速和弹性模量的影响规律。

1 超声脉冲法和冲击回波法测试原理

1.1 超声脉冲法

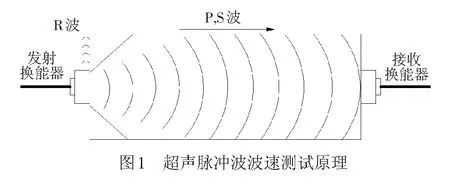
声波仪通过发射换能器向待测试件发射声波脉冲时，脉冲波在传播过程中分别产生P波、S波和R波，见图1。因P波传播速度最快而被接收换能器最先接收到，其在试件中的表观波速为

Vp1=S/T0

( 1 )

式中：Vp1为超声脉冲波P波的表观波速；S为声程；T0为首波声时。

在三维弹性介质中超声脉冲波P波波速与弹性模量的关系为[8]

( 2 )

式中：ρ为材料密度；E、ν分别为材料的弹性模量和泊松比。

文献[9]的研究表明：当试件横向最小尺寸大于声波波长时，P波波速与弹性模量间的关系可近似采用式( 2 )。本文测试时超声脉冲波的采样频率为50 kHz，RPC中的波速一般为4 000～5 000 m/s[8]，则波长为80～100 mm，满足式( 2 )的使用条件。

1.2 冲击回波法

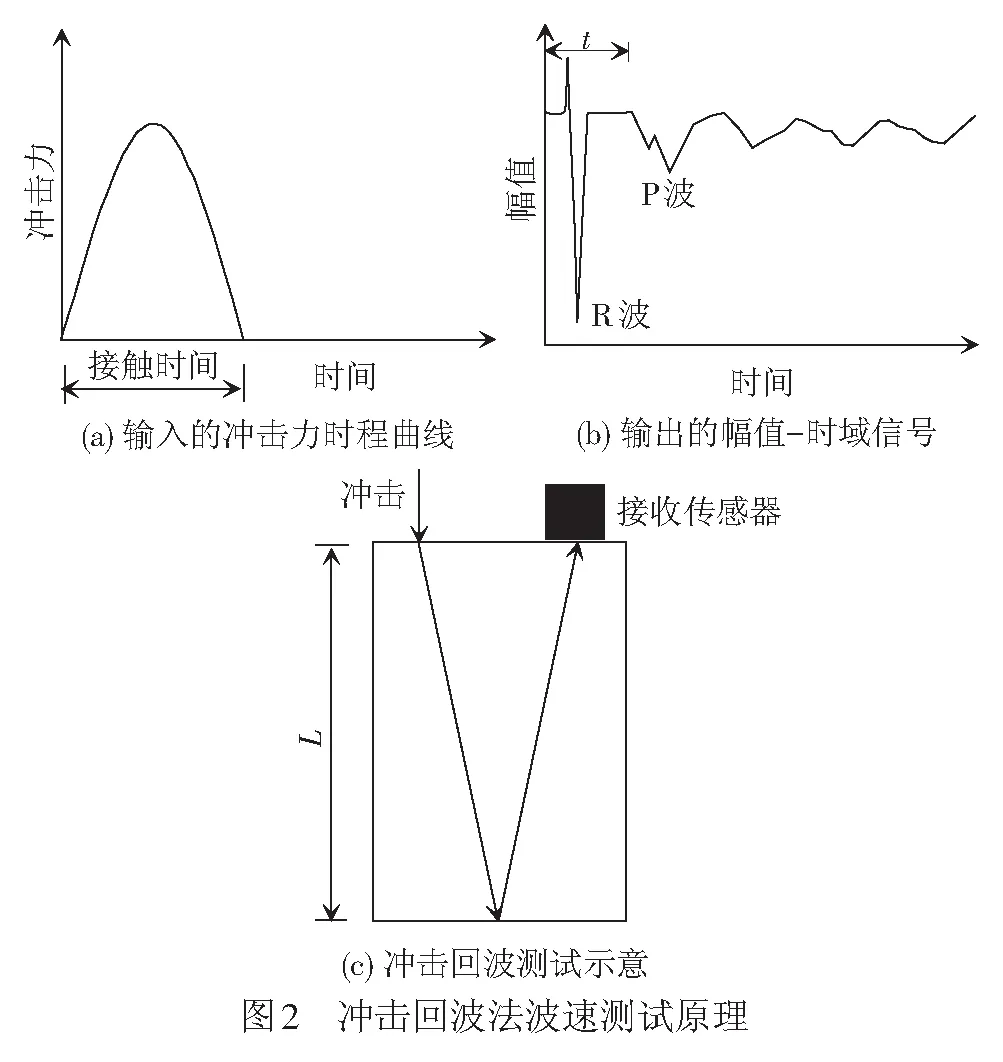
冲击回波法测试时，通过在被测试件表面施加弹性冲击而产生低频弹性应力波并在物体上、下两个表面之间形成重复反射，见图2。接收传感器接收到的反射波，经去除R波信号并采用傅里叶变换后，在反射波频谱图上出现一个与P波卓越频率相应的幅度峰值，其表观波速为[6]

Vp2=2Lf

( 3 )

式中：Vp2为冲击回波P波的表观波速；L为所测试件长度；f为卓越频率。

文献[6]的研究成果表明：当所测试构件为棒状(试件高宽比≥2)时，表观波速可认为与一维弹性介质中的纵波波速相等。因此对于本文高宽比为3的测试试件(100 mm×100 mm×300 mm)，其表观波速与弹性模量间的关系为[6]

( 4 )

2 试验概况

为研究强度等级和钢纤维掺量对RPC波速和弹性模量的影响规律，建立RPC动、静弹性模量间的定量关系，配制了3种强度等级(分别为RPC100、RPC140、RPC160)、4种钢纤维体积掺量(分别为0%、1%、2%、3%)的RPC，分别制作了RPC棱柱体和立方体试件各12组，每组3个试件，共计72个试件。

2.1 配合比及材料

试验采用3种不同强度等级RPC(RPC100、RPC140、RPC160)的配合比，见表1。水泥采用PO52.5普通硅酸盐水泥，其28 d抗折强度为9.91 MPa，抗压强度为57.5 MPa；硅灰采用800目精制硅灰；RPC100和RPC140采用级配砂，粒径构成为粗砂(0.63～1.25 mm)∶中砂(0.315～0.630 mm)∶细砂(0.160～0.315 mm)=2∶4∶1；RPC160采用标准砂，粒径范围为0.5～1.0 mm；石英粉采用300目精制石英粉；钢纤维采用表面镀铜平直钢纤维，直径0.2 mm，长度13 mm，长径比65，抗拉强度不小于 1 850 MPa；采用聚羧酸高效减水剂，减水率30%，含固量40%。

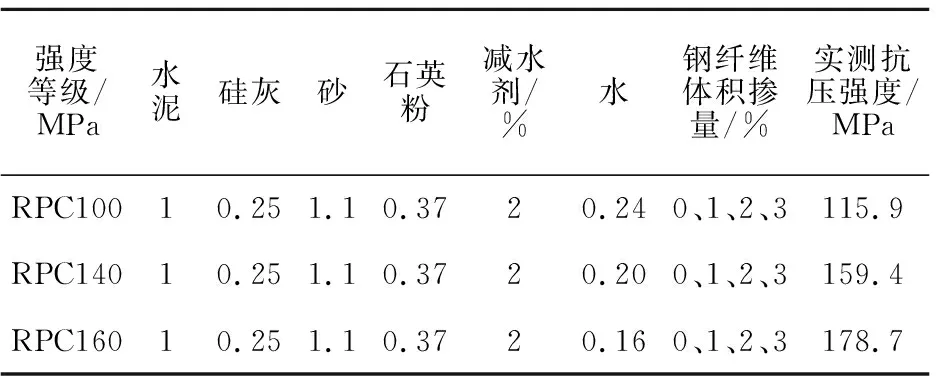
表1 不同强度等级RPC的配合比及实测抗压强度

注：1.RPC配合比中除钢纤维为体积掺量外，其余各组分均为质量比；2.实测抗压强度为钢纤维掺量为2%的100 mm立方体试块抗压强度平均值。

2.2 试件制作及养护

按配合比称量各组分，首先将石英砂放入强制式搅拌机中，其次将钢纤维倒入搅拌4～5 min后加入水泥、硅灰与石英粉继续搅拌4～5 min至均匀，将减水剂与水拌合后，倒入一半于搅拌机中继续搅拌3 min，最后把剩余的水和减水剂倒入，继续搅拌4～7 min结束。将混凝土装入模具中，在高频振捣台上振捣成型后放入标养室，24 h后拆模，然后将试件放入蒸汽养护箱按照文献[1]进行蒸汽养护。共制作了12组棱柱体(100 mm×100 mm×300 mm)和12组立方体试件(100 mm×100 mm×100 mm)，成型试件见图3。

2.3 试验装置及方法

采用非金属超声检测仪进行超声脉冲法测试，工作频率为50 kHz；冲击回波法采用IES扫描式冲击回波测试仪，工作频率为5 kHz；静态弹性模量测试则采用2 000 kN压力试验机控制加卸载。

超声脉冲法测试依据文献[10]的要求，采用对测法进行波速测试，换能器与试件表面用凡士林耦合，每个试件设置5个测点，所测得波速取5点波速均值；冲击回波测试则采用冲击器冲击混凝土表面，得到冲击位置附近反射波振动-时间曲线，进行快速傅里叶变换后得到反射波的频谱，频谱图上突出的峰值是应力波在混凝土试件底面反射形成，每个试件连续进行10次数据采集然后取均值；静弹性模量测试时，首先在双端面磨平机上将试件的两个加载面磨平，然后在试件4个侧面对称位置分别贴上电阻应变片，加载规则按照文献[4]的规定进行，测试方法见图4。

3 试验结果与分析

主要测试结果见表2。采用电子称测定试件质量M、排水法测定体积V后获得试件的表观密度。随着钢纤维的增加，混凝土密度逐渐增大。表中基于超声脉冲法和冲击回波法所得表观波速Vp1和Vp2均为实测数据，相应的动弹性模量Ed1和Ed2分别采用式( 2 )和式( 4 )计算，式( 2 )中的泊松比采用实测值，静弹性模量Es根据文献[4]的规定实测得到。

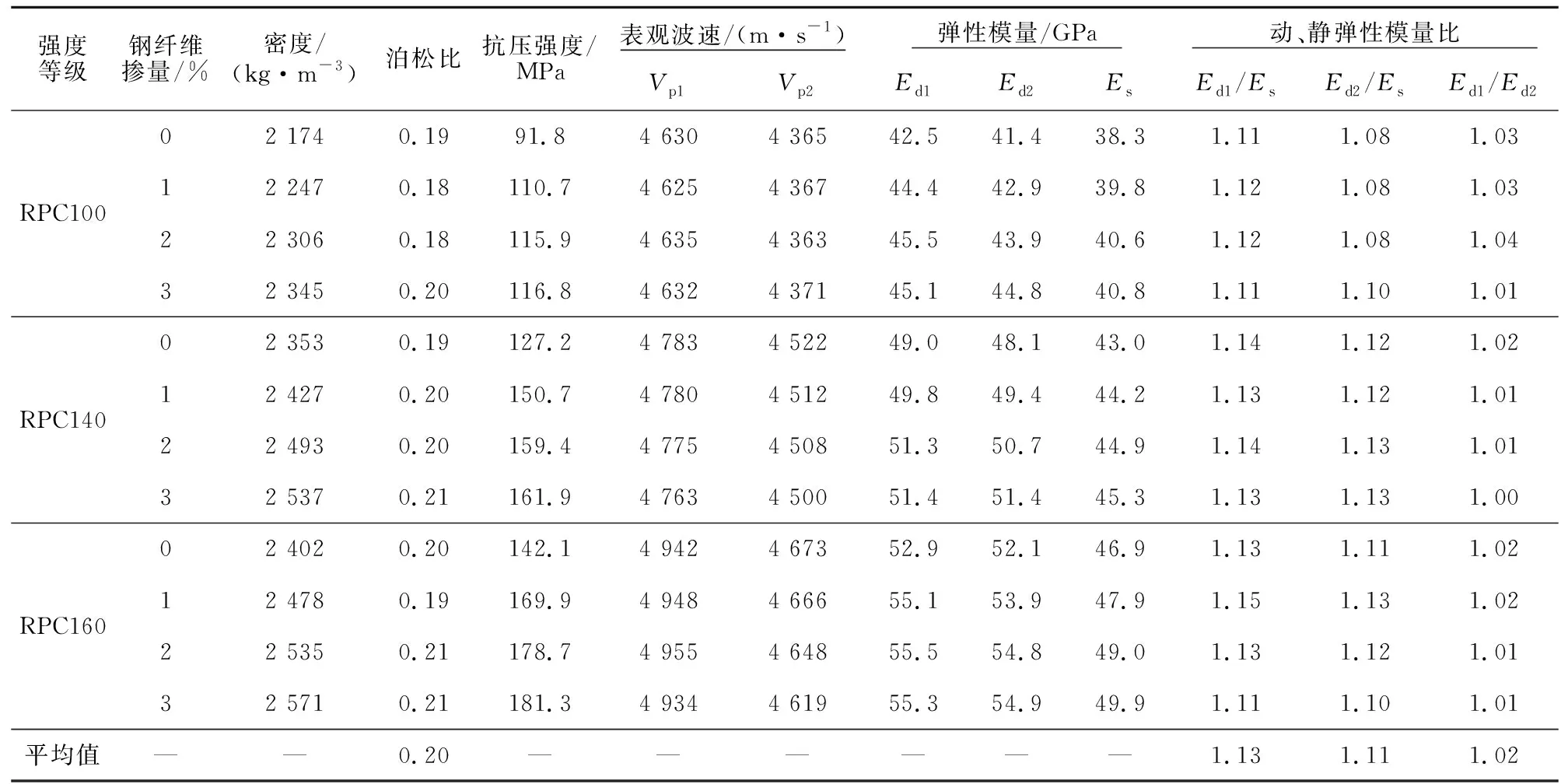
表2 试验结果

3.1 抗压强度与泊松比

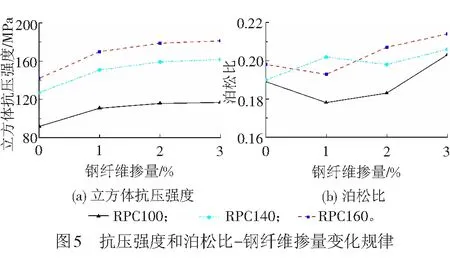
RPC立方体抗压强度及泊松比随钢纤维掺量的变化规律见图5。由图5(a)可见：RPC立方体抗压强度均随钢纤维掺量的增加而提高，钢纤维掺量为1%、2%、3%时的抗压强度较钢纤维掺量0%时分别提高19.6%、25.8%、27.4%，钢纤维掺量从0%～1%时RPC抗压强度增幅最大为19.6%，当钢纤维掺量达到2%以后，增强效果不显著，钢纤维从2%～3%强度仅提高1.6%。其主要原因是掺入钢纤维改变了试件的破坏模式。掺钢纤维试件的破坏模式由素RPC试件的锥形脆性破坏转化为对角剪切或微柱型延性破坏，由于分布于滑移面钢纤维的桥接作用，使摩阻角增大而提高强度。但随着钢纤维掺量的进一步增加，搅拌过程中钢纤维成团的问题加剧，其桥接效果减弱，使得抗压强度提升幅度减小。

进行泊松比测试时，试件承受的最大应力仅为峰值应力的40%，处于弹性状态。由图5(b)可见，RPC的泊松比与钢纤维掺量和强度等级间无明显的规律性，本次试验各组试件的泊松比变化范围为0.18～0.21，均值为0.20，与普通混凝土的泊松比0.2基本相同[11]。

3.2 表观波速

超声脉冲法和冲击回波法所得表观波速随钢纤维掺量及强度等级的变化规律见图6。由图6(a)可见，不同强度等级试件的表观波速差异较大，160 、140 MPa的表观波速较100 MPa分别增大了6.7%、3.2%。但同一强度的RPC中，钢纤维掺量对表观波速的影响甚小，其最大变化量不超过1.2%。这是因为强度等级越高，水胶比越小， RPC内部更加密实，所测表观波速越大。但钢纤维掺量对RPC试件内部密实度影响较小，其作用主要在试件加载开裂后才得以体现，故钢纤维掺量对零应力时的表观波速影响甚小。

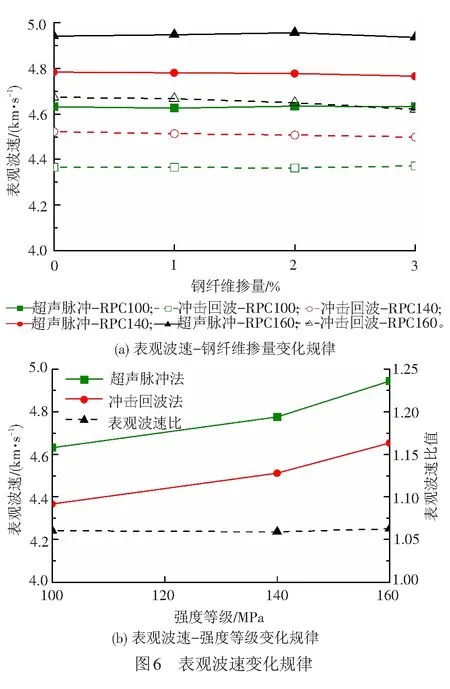
为此，不考虑钢纤维掺量影响，将各强度等级表观波速取均值，得到表观波速随强度等级的变化规律，见图6(b)。两种方法所测表观波速均随RPC强度等级的提高而增大，且超声脉冲法表观波速大于冲击回波法。3种强度等级下两者的比值分别为1.060、1.059、1.063，平均值为1.06，两种无损检测方法所测表观波速之间的比值与强度等级无关。

3.3 弹性模量

3.3.1 静弹性模量

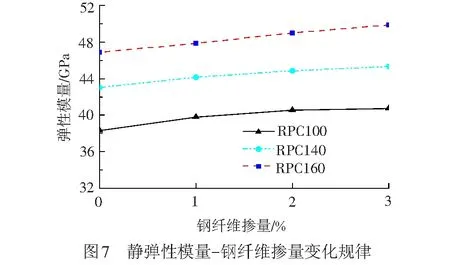
实测静弹性模量随钢纤维掺量的变化规律见图7。由图7可知，随着钢纤维掺量的增加，RPC的弹性模量逐渐增大，但提高幅度有限，钢纤维掺量3%较0%时仅提高6.0%；RPC弹性模量随强度等级的提高变化明显，160、140 MPa RPC的弹性模量较100 MPa的分别提高21.4%、11.2%。

3.3.2 动、静弹性模量关系

由表2可知，采用超声脉冲法和冲击回波法测定的不同强度等级和不同钢纤维掺量试件的动弹性模量相差仅在2%左右，且超声脉冲法所测动弹性模量稍高，两种动弹性模量皆较静弹性模量大10%左右。

导致这种现象的原因主要有两方面，首先，两种方法测试时混凝土应力应变状态不同。动态弹性模量是在低应力条件下测得，接近于原点切线模量，而静态弹性模量则在较高应力下测定，为割线模量；其次，RPC的非匀质性对不同测试方法的影响各异。试件成形过程中不可避免存在些微小裂缝和空隙，这将导致应力状态下静弹性模量的降低，但超声波或者冲击回波的波长远大于这些空隙，使得传播波速基本不受影响。

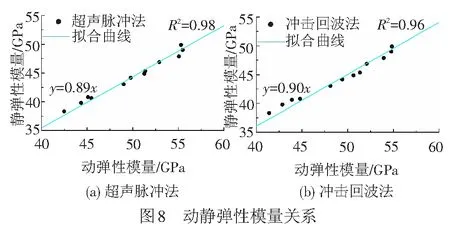
动弹性模量与静弹性模量关系见图8。由图8可知，采用超声脉冲法和冲击回波法所测动态弹性模量与静弹性模量间均存在较强的线性相关性，两者间的关系可表示为

Es=αEd

( 5 )

式中：超声脉冲法的α值为0.87～0.90，均值0.89；冲击回波法的α值为0.89～0.93，均值0.90；综合建议两种方法下的α均取值为0.90。因此，可由动弹性模量Ed推导出RPC的静弹性模量Es。

3.3.3 静弹模量与抗压强度关系

参照规范[11]中普通混凝土弹性模量与立方体抗压强度间的关系模型，基于文献[15-26]和本文的试验数据，采用最小二乘法，拟合得到RPC静态弹性模量与其抗压强度间的定量关系式为

( 6 )

式中:fcu为立方体抗压强度(试件尺寸100 mm),MPa。

其中，样本总数为88，抗压强度分布区间为91.8～234.9 MPa，弹性模量分布区间为38～57 GPa，养护条件为热水养护或蒸汽养护，水胶比为0.16～0.24，钢纤维掺量0～4%，且大部分数据为水胶比0.2和钢纤维掺量2%时的RPC。

钢纤维混凝土的弹性模量计算式与普通混凝土相同为[12]

( 7 )

式中：fcu,k为立方体抗压强度标准值，MPa。

高强混凝土的弹性模量计算式为[13]

( 8 )

活性粉末混凝土弹性模量计算式为[14]

( 9 )

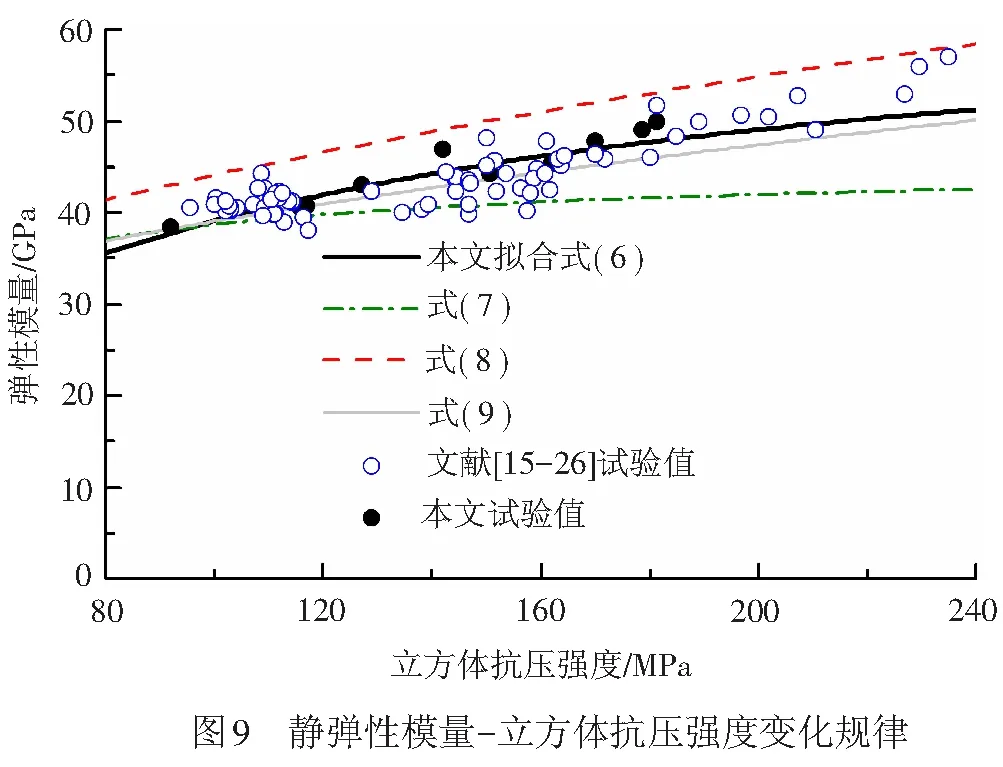
采用式( 6 )～式( 9 )计算得到的弹性模量与试验结果对比见图9。由图9可见，基于RPC试件结果提出的式( 6 )和式( 9 )与试验结果吻合较好；式( 7 )实为普通混凝土弹性模量的预测公式，其计算结果较试验值低；式( 8 )为高强混凝土的相应预测公式，计算结果高于试验值，表明高强混凝土中高强粗骨料的存在可提高混凝土的弹性模量，虽然式( 7 )、式( 8 )并非针对RPC提出，但由此可定性看出RPC的弹性模量介于钢纤维混凝土和高强混凝土弹性模量之间。

4 结论

采用静力法、超声脉冲法和冲击回波法测试了不同强度等级和不同钢纤维掺量活性粉末混凝土的强度及弹性模量，得到以下结论：

(1) RPC中的钢纤维掺量对其抗压强度、弹性模量的影响较小，钢纤维掺量为3%时的弹性模量较钢纤维掺量0%仅提高6.0%；但RPC动静弹性模量均随抗压强度等级的提高而增大，160、140 MPa 强度等级RPC的弹性模量较100 MPa分别提高21.4%、11.2%。

(2) 采用超声脉冲法所测表观波速为冲击回波法表观波速的1.06倍；两种方法所测表观波速均随着强度等级的提高而增大，但钢纤维掺量对其影响甚小，表观波速最大变化量不超过1.2%。

(3) 超声脉冲法和冲击回波法所测动弹性模量均大于静弹性模量，但两者存在良好线性关系，RPC静弹性模量约为动弹性模量的0.9。

(4) 基于试验数据建立了RPC静弹性模量与立方体抗压强度的统计关系，且当抗压强度相近时，RPC的弹性模量介于钢纤维混凝土和高强混凝土弹性模量之间。