浅谈三角形中的最值问题及解法
■重庆市铁路中学校 何成宝
解三角形中的最值问题,在近几年各类考试中频繁出现,颇受命题者的青睐。这类问题的实质是将几何问题转化为代数问题,主要运用三角形的内角和定理、正余弦定理、面积公式、三角恒等变形、三角函数的性质,以及基本不等式等知识解题。下面举例说明三角形中最值问题的类型及解法,供同学们参考。
一、已知角的等量关系

点评:①本题容易忽视“△ABC是锐角三角形”这个条件。②本题涉及三角形边角之间的关系,考查边角互化知识,化多元为一元,体现了解题的通性通法。
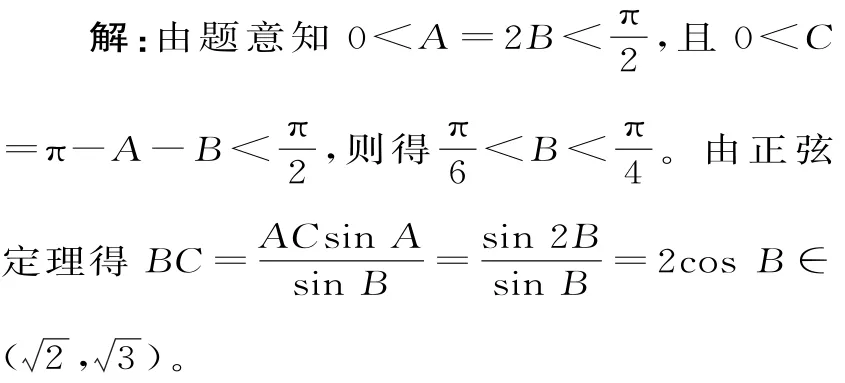
练习:在锐角△ABC中,A=2B,AC=1,则BC的取值范围是。
二、已知一边和该边的对角
例2 在△ABC中,角A,B,C的对边分别为a,b,c,且b=5,B=,求△ABC的周长的取值范围。

点评:对三角函数式的处理常常借助于同角三角函数间的关系、诱导公式以及恒等变换式等实施变形,达到化简、求值的目的。
练习:在△ABC中A,B,C所对的边分别为a,b,c,且a=,A=,求△ABC的面积的最大值。

三、已知三边的等量关系
例3 在△ABC中,a2+b2=c2+ab,若△ABC的外接圆半径为△ABC的面积的最大值为。

又由于c=2RsinC=4,所以c2=a2+b2-2abcosC ,16+,即ab≤12。
点评:先利用余弦定理求cosC的大小,再求出sinC的大小,然后利用三角形的面积公式结合基本不等式,求三角形面积的最大值。
练习:若△ABC的三边a,b,c成等比数列,a,b,c所对的角依次为A,B,C,则sinB+cosB的取值范围是。
解:由题设知b2=ac。

点评:本题将数列、基本不等式、三角函数、解三角形等知识结合起来,有利于提高同学们的综合解题能力。
四、已知一边和另两边的等量关系


点评:本题结合函数的知识,以同学们熟悉的三角形为载体,考查了三角形的面积公式、余弦定理等知识,是一道考查解三角形的好题。
练习:已知△ABC中,AB=2,AC=3BC,则△ABC面积的最大值是。解:设BC=x,则AC=3x。根据面积公式得:

五、已知向量的等量关系



