解三角形知识大闯关
■河南省洛阳市汝阳一高 张海涛
解三角形是初中解直角三角形问题的直接延伸,也是三角函数和平面向量知识考查的重要载体,同时也是解决三角形中计算问题及生产、生活实际问题的重要工具,具有重要的应用价值,属于高考的必考内容。主要通过三组公式(正弦定理、余弦定理、面积公式),通过问题导学,激活知识构建的前后联系。解决问题的基本方法主要是通过边角互化,即“化角为边(代数恒等变换),化边为角(三角恒等变换)”来实现优化解题,要求对公式、定理灵活运用,能够逆用、变形使用等,通过余弦定理建立三边关系,通过正弦定理建立边角关系,转化为三角函数问题或者借助三角形的某一顶点的轨迹,借助图形,如外接圆来解决。从角的思路解题较为烦琐,但是具有通用性;从形的角度解题,通过临界位置,可以求解最值;从三角、三边之外的非基本元素,如高、中线、角平分线等入手,比较灵活,结合方程思想、化归思想可以解决三角形有关的动态问题,如有关角、边、面积、周长的范围问题。总之,解三角形问题近年来试题内容丰富多彩,集知识的交汇性、综合性于一体,极富挑战性,值得我们重视。
下面,我们依据题目的特点把解三角形问题大致归纳为如下几个类型,便于让同学们做一题而知一类,触类旁通,提高学习效率。
第一关:边、角、周长、面积具体求值问题
(一)求边。


试题点评:解法1是运用正弦定理“边化角”,而使用正弦定理的一个基本条件是“齐次”,因此,结合条件a2-c2=2b得到b=就是非常自然的事情,然后再使用正弦定理并结合条件求出b;解法2则是运用余弦定理“角化边”,结合题目所求“直奔主题”。本题还有很多求解方法,读者可以自行尝试。
(二)求角。
例2 已知在△ABC中角A,B,C的对边分别为a,b,c,且2(a2-b2)=2accosB+bc,则A=。
解法1(化角为边):由余弦定理得a2+c2-b2=2accosB。
代入已知条件,得:2(a2-b2)=a2+c2-b2+bc,故a2-b2-c2=bc。

解法2(化 边 为 角):由2(a2-b2)=2accosB+bc及正弦定理可得:
2sinAsinCcosB+sinBsin C=2(sin2A-sin2C)=2sin(A+B)sin(A-B)=2sinCsin(A-B)。
因为sinC>0,故2sinAcosB+sinB=2sin(A-B),sin B=-2sinBcosA,所以cosA=-,A=。
试题点评:解法1是观察所求与条件发现可利用余弦定理消除角,得到边的关系,再次利用余弦定理恰好求得角A;解法2则根据所给条件两边为齐次结构,恰好可以利用正弦定理边化角,对恒等式左侧利用两角正弦的平方差公式sin2A-sin2B=sin(A+B)·sin(A-B)实现降次,结合和差公式逆用求得角A。
(三)求周长。
例3 在△ABC中,角A,B,C所对的边分别为a,b,c,若b=5,C=60°,且△ABC的面积为5,则△ABC的周长为。
所以△ABC的周长为9+21。
试题点评:要求周长需先求a,c,观察所给边角及面积三个条件发现恰好可以求解a,进而根据知三求二利用余弦定理得到边c,从而完成周长求解。
(四)求面积。
例4 在△ABC中,角A,B,C所对的边分别为a,b,c,若A=,a=4,角A的平分线交边BC于点D,其中AD=3,则△ABC的面积S△ABC=。

在△ABC中根据余弦定理可得:b2+c2-bc=112。②
联立①②可得bc=48。故S△ABC=bcsinA =12。
试题点评:题目给出了含有边的三个条件,但这三个条件是“分散”的,要想求出面积,如何将条件AD=33转化成“有用”的条件是解题的关键。解法1是设法求出∠ADC的正弦值,再根据△ABC是△ABD和△ADC之和,应用正弦定理求解;解法2则是根据S=bcsin A,综合利用题目△ABC所给条件求出bc,从而求出面积。
第二关:求解边、角、周长、面积的范围与最值及判断三角形形状问题
(一)求边的范围与最值问题。
例5 已知△ABC的内角A,B,C的对边分别为a,b,c,且(a2+b2-c2)(acosB+bcosA)=abc,若a+b=2,则c的取值范围为( )。

试题点评:观察所给条件中的结构acosB+bcosA,根据射影定理得到其恰好为c,进而实现角化边,自然想到利用余弦定理求解角C,再次利用余弦定理得c2=4-3ab,观察条件a+b=2想到利用基本不等式求解最大值,结合三角形三边关系求得周长范围。
(二)求角的范围与最值问题。
例6 在△ABC中,若tanA,tanB,tanC依次成等比数列,则∠B的取值范围为。
解法1(余弦定理+基本不等式):sinCcos2B。
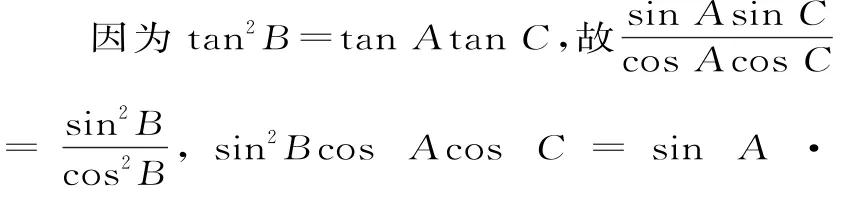

解法2(正弦定理+余弦定理):
由tan2B=tanAtanC及正弦定理得:

试题点评:解法1中,初看题目自然想到要进行切角化弦,得到sin2BcosAcosC=sinAsinCcos2B,两边角的名称恰好互余,只能用正弦、余弦定理继续化简,发现b2=,确实复杂,继续进行,再看目标是求角B的范围,利用余弦定理将cosB转化为a,c的齐次式,柳暗花明,利用基本不等式恰好得到其范围,进而求得角B的范围。

(三)求周长的范围与最值问题。
例7 在锐角△ABC中,角A,B,C所对的边分别为a,b,c,且c=1,A=2C,则△ABC的周长的取值范围为。

(四)求面积的范围与最值问题。
例8 在△ABC中,a,b,c为角A,B,C的对边,若a2+b2+2c2=8,则面积的最大值为。


解法3:由题意和余弦定理得8=a2+b2+2(a2+b2-2abcosC)=3(a2+b2)-4abcosC≥2ab(3-2cosC)。
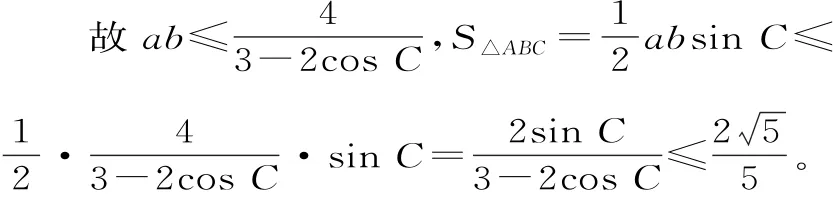
试题点评:本题难度较大,仅仅给出边的关系,要求面积的最大值,结合面积公式包含的元素——两边及其夹角的正弦,自然想到通过通过两个定理转化为边或角的函数,利用不等式性质求解其最大值,或者转化为角的关系,利用定点与单位圆上点的连线的斜率的范围求解。
(五)三角形形状的判定问题。
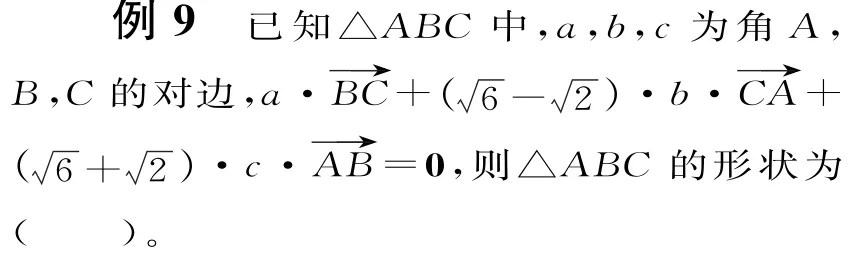
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
由图2中A可知,添加酶的试验组中,辣椒碱、辣椒二氢碱和辣椒红色素的含量均较空白组高。且由图2中B可知,3种物质的含量随酶添加量的增大而增大,在酶添加量为0.3%(W/W)时,辣椒碱、辣椒二氢碱的含量达到最大值。在酶添加量为0.2%(W/W)时,辣椒红色素的含量达到最大。分析原因可能是,当酶添加量较低时,底物过量,酶解不完全,致使辣椒中的有效成分溶出率不高,随着酶添加量的增加,酶解作用增加,辣椒中关键物质的溶出率也随着增加,而当酶添加过量时,由于酶与底物的结合饱和,3种物质的含量不会继续增长。


试题点评:判断三角形的形状应围绕三角形的边角关系进行思考,可用正、余弦定理将已知条件转化为边边关系,通过因式分解、配方等方式得出边的相应关系,从而判断三角形的形状,也可利用正、余弦定理将已知条件转化为角与角之间的关系,通过三角变换,得出三角形各内角之间的关系,从而判断三角形形状。
第三关:多知识点融合问题
(一)求参数问题。
例10 在△ABC中,角A,B,C的对边分别为a,b,c,已知sinA+sinB+λsinAsinB=0,且a+b=2c,则实数λ的取值范围是。
解:由a+b=2c结合正弦定理可得sinA+sinB=2sinC。


(二)与向量结合的问题。
例11 若G为△ABC的重心,且AG⊥BG,则sinC的最大值为。
解法1(向量夹角+基本不等式):

试题点评:解法1通过赋值,结合三角形法则及直角三角形斜边中线性质及重心性质巧妙构造方程组,得到根据整体性把握,立刻会想到利用基本不等式去解决;解法2的解题思路殊途同归,重在利用据数量积为0转化得到结论再利用不等式解决。
(三)求比值问题。

解法2(余弦定理+余弦函数有界性):

第四关:解三角形的实际应用问题
(一)求解高度问题。

图1
例13 如图1,飞机的航线和山顶在同一个铅垂平面内,已知飞机所在处的海拔为20210m,速度为270m/s,飞行员先看到山顶的俯角为15°,经过100s后又看到山顶的俯角为30°,则山顶的海拔为。
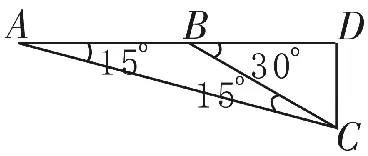
图2
答案:6710m
解析:如图2。
AB=270×100=27
000
(m),在等腰三角形ABC中,BC=AB=27
000
试题点评:求解高度问题应注意:(1)在测量高度时,要理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内,视线与水平线的夹角;(2)准确理解题意,分清已知条件与所求,画出示意图;(3)运用正、余弦定理,有序地解相关的三角形,逐步求得问题的答案,注意方程思想的运用。
(二)测量距离问题。

图3
例14 如图3所示,从气球A测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高度是60
m,则河流的宽度BC等于( )。
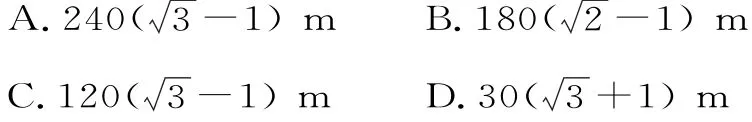
答案:C
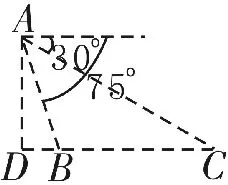
图4


试题点评:求解距离问题应注意:(1)选定或确定要求解的三角形,即所求量所在的三角形,若其他量已知则直接解;若有未知量,则把未知量放在另一确定三角形中求解。(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理。
(三)解决测量角度问题。
例15 甲船在A处观察到乙船在它北偏东60°的方向,两船相距akm,乙船正在向北行驶,若甲船的速度是乙船的3倍,则甲船应取北偏东θ方向前进,才能尽快追上乙船,此时θ=。
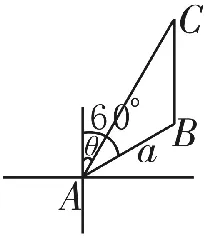
图5
答案:30°
解析:如图5所示,∠CAB=60°-θ,∠B=120°,设追上乙船的时间为x,则BC=x,AC=x,在△ABC中,根据正弦定理得即,解得sin(60°-θ)=,又60°-θ为锐角,所以60°-θ=30°,θ=30°。
试题点评:求解测量角度问题应注意:(1)明确方位角的含义;(2)分析题意,分清已知与所求,再根据题意正确画出示意图,这是最关键、最重要的一步;(3)将实际问题转化为可用数学方法解决的问题后,注意正、余弦定理的“联袂”使用。
第五关:能力提升专训

2.如果不等式ksin2B+sinAsin C>19sinBsinC对任意△ABC都成立,则实数k的最小值为。
解(正弦定理+三边关系):

解:设a,b,c分别为角A,B,C的所对的边,由题意得b=c+1,a>2。
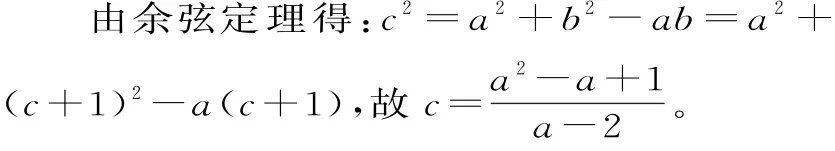
所以△ABC的周长为:

4.在△ABC中,内角A,B,C的对边分别为a,b,c,且BC边上的高为取得最大值时,内角A的值为。
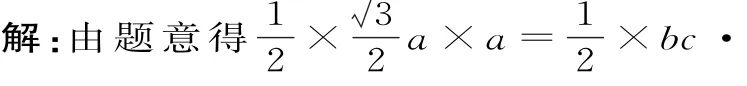


图6

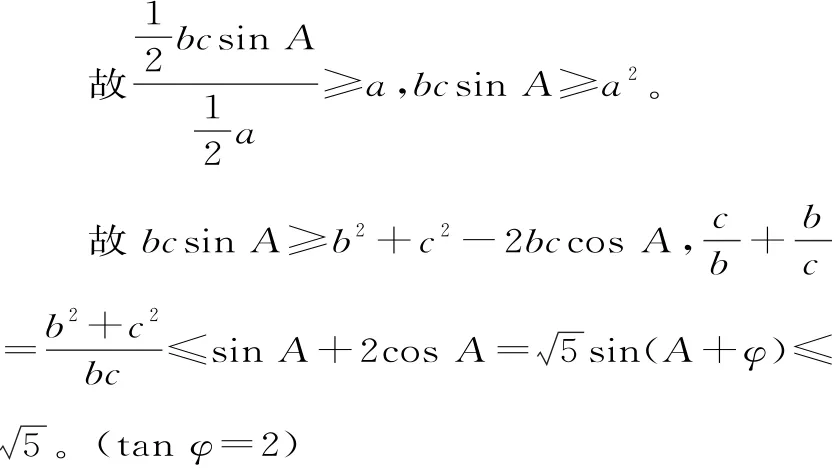
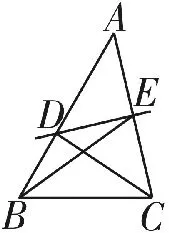
图7


解:先考虑一般情况,如图8所示。
设∠PAC=α,∠PAB=β,PA=a,其中α,β为常数,∠APC=x(x为变量)。
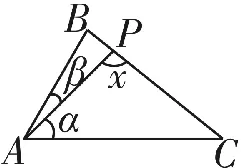
图8



图9
解法2(引入变量构造方程组):如图9,取D,E两点,使AD=BD,作DE⊥AC于点E,设DE=3t,则CD=5t,CE=4t,AE=66t,AD=BD=15t。

解法3(利用正弦定理及积化和差公式):
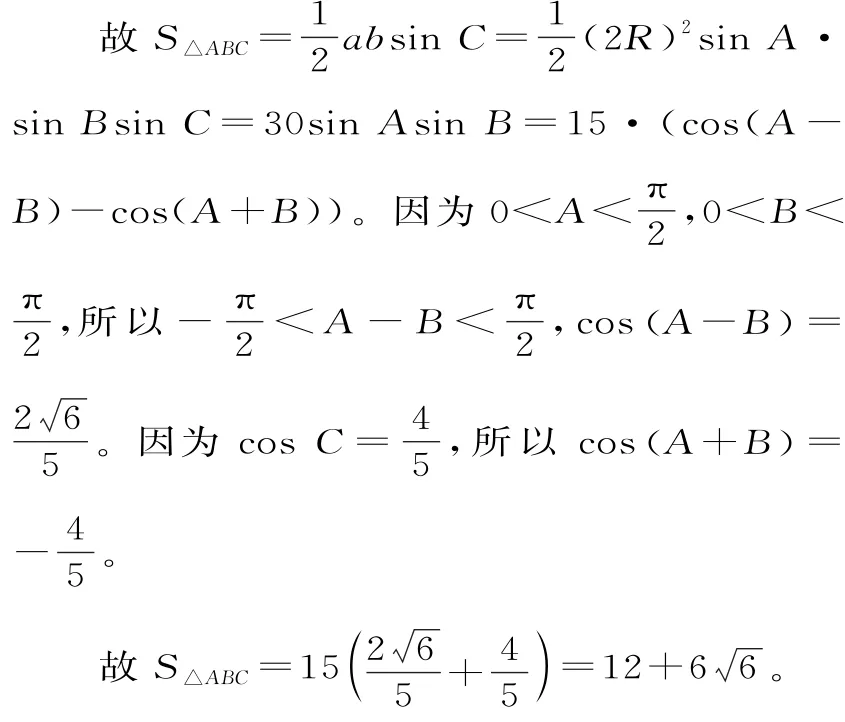
10.在△ABC中,ccosB+3bcosC=0,则角A的最大值为。

11.△ABC中,A,B,C成等差数列,a2+c2=kb2,则实数k的取值范围是。


A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰或直角三角形

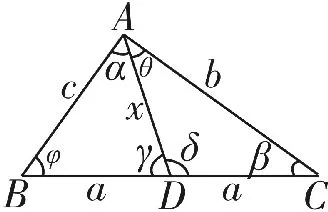
图10

解法2:如图11所示,AE为△ABC外接圆的直径。
(1)D与O不重合,则AE⊥BC,△ABC为等腰三角形;
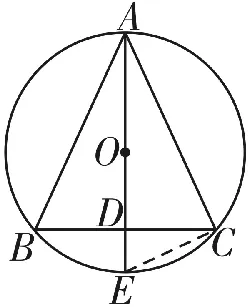
图11
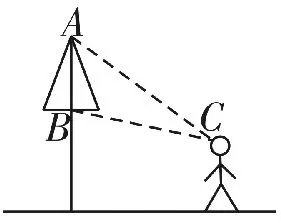
图12
A.2.2 B.2
C.1.8 D.1.6


