说说三角形面积公式的应用
■河南省潢川县高级中学高三(20)班 白羽晗
在△ABC中,若三个内角A、B、C所对的边分别为a、b、c,则这个三角形的面积S=三角形的面积公式看似简单,应用却十分广泛,下面举例说明。
一、应用三角形面积公式求面积
分析:已知AB和AC,只需求出两边的夹角A,就可以利用三角形的面积公式求解。

因此,B=30°。
从而A=180°-120°-30°=30°。

评注:求三角形的面积问题,先观察已知什么,缺少什么,用正弦定理、余弦定理求出需要的元素,就可以求出三角形的面积。当遇到求四边形面积时,可以转化为求两个三角形的面积之和。
二、应用三角形面积公式求角
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S(a2+b2-c2),则角C的大小为_____。
分析:把三角形面积公式看成以所求角为未知数的方程来求解。

评注:应用三角形面积公式求角时,同样要特别注意解的个数,判断解的个数可依据三角形的几何性质和三角函数的单调性。
三、应用三角形面积公式求边
例3 (1)在△ABC中,已知AB=3,A=120°,且△ABC的面积为边的长为。
(2)设△ABC的内角A,B,C所对的边长分别为a,b,c,且cosB=,b=2。当△ABC的面积为3时,求a+c的值。
分析:(1)先应用三角形面积公式求出AC,再结合余弦定理求BC边的长。
(2)将三角形面积公式和余弦定理看成关于a,c的方程组。

评注:利用正弦定理、余弦定理、面积公式将已知条件转化为方程组是解决复杂问题的常见思路,将方程化为只含边的式子或只含角的三角函数式,然后化简并考察边或角的关系,最终求解。
四、三角形的面积公式的综合应用
例4 在△ABC中,角A,B,C所对的边分别为a,b,c,并且cos2C+22cos
C+2=0。
(1)求角C的大小;
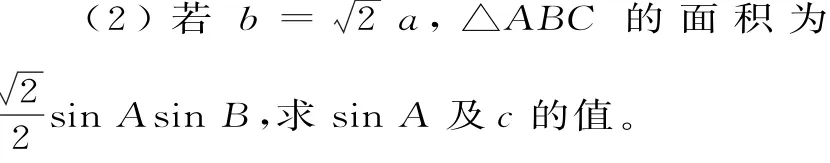
分析:(1)利用余弦倍角公式,将题设中的三角方程化为关于cosC的二次方程,从而求得角C的大小;(2)综合应用余弦定理、三角形面积公式和正弦定理求解。
解:(1)因为cos2C+22cos
C+2=0,所以2cos2C+22cosC+1=0。

评注:题目条件或结论中若涉及三角形面积的综合题,除根据题意灵活选用三角形的面积公式外,还要用到正弦、余弦定理及三角函数、三角恒等变换、方程等知识。

