地铁牵引供电系统失效的故障树分析
林小松 杨 俭 袁天辰
(上海工程技术大学城市轨道交通学院,201620,上海//第一作者,讲师)
现有地铁牵引供电系统故障树分析主要针对接触网部分展开定性分析和定量计算[1-7]。先通过定性分析,利用行列式法、结构法及布尔代数法等求解地铁接触网系统故障的最小割集[8-9];在此基础上再进行定量计算,获得地铁接触网系统不可靠度、平均无故障运营时间等。目前,针对地铁牵引供电系统的整体故障树分析与研究比较少[4]。
1 地铁牵引供电系统及其常见故障
1.1 牵引供电系统
地铁牵引供电系统组成如图1所示。首先,交流电由城市电网进入地铁电网主变电所,而后进入牵引变电所。然后,馈线将牵引变电所输出的直流电输送到接触网;由地铁列车通过受电弓从接触网取电。最后,由回流线将地铁轨道的电流导向牵引变电所。可见,在地铁牵引供电系统中,走行轨道构成了供电回路的一部分[12]。
1.2 地铁牵引供电系统常见故障
根据文献[10-14],统计国内常见的地铁牵引供电系统故障现象与原因。统计结果见表1。
2 地铁牵引供电系统失效故障树模型
故障树分析法是安全系统工程中的重要分析方法,其目的是找出安全系统工程中的基本故障,并确定故障原因、影响大小和发生概率[4,7]。故障树分析需自上而下、一层层寻找顶事件的直接原因事件和间接原因事件,直到基本原因的底事件。
根据国内部分地铁牵引供电系统失效故障的调研数据,结合文献[1-4],确定了牵引供电失效故障的底事件及其发生概率(见表2)。
通过对表3中的底事件进行相关分析,可绘制出逻辑框图,从而得到地铁牵引供电系统失效故障的各种原因组合可能。同时,通过计算牵引供电系统平均无故障运营时间,可得到相应的纠正措施,从而提高地铁牵引供电系统可靠性。地铁牵引供电系统失效的故障树模型如图2所示。
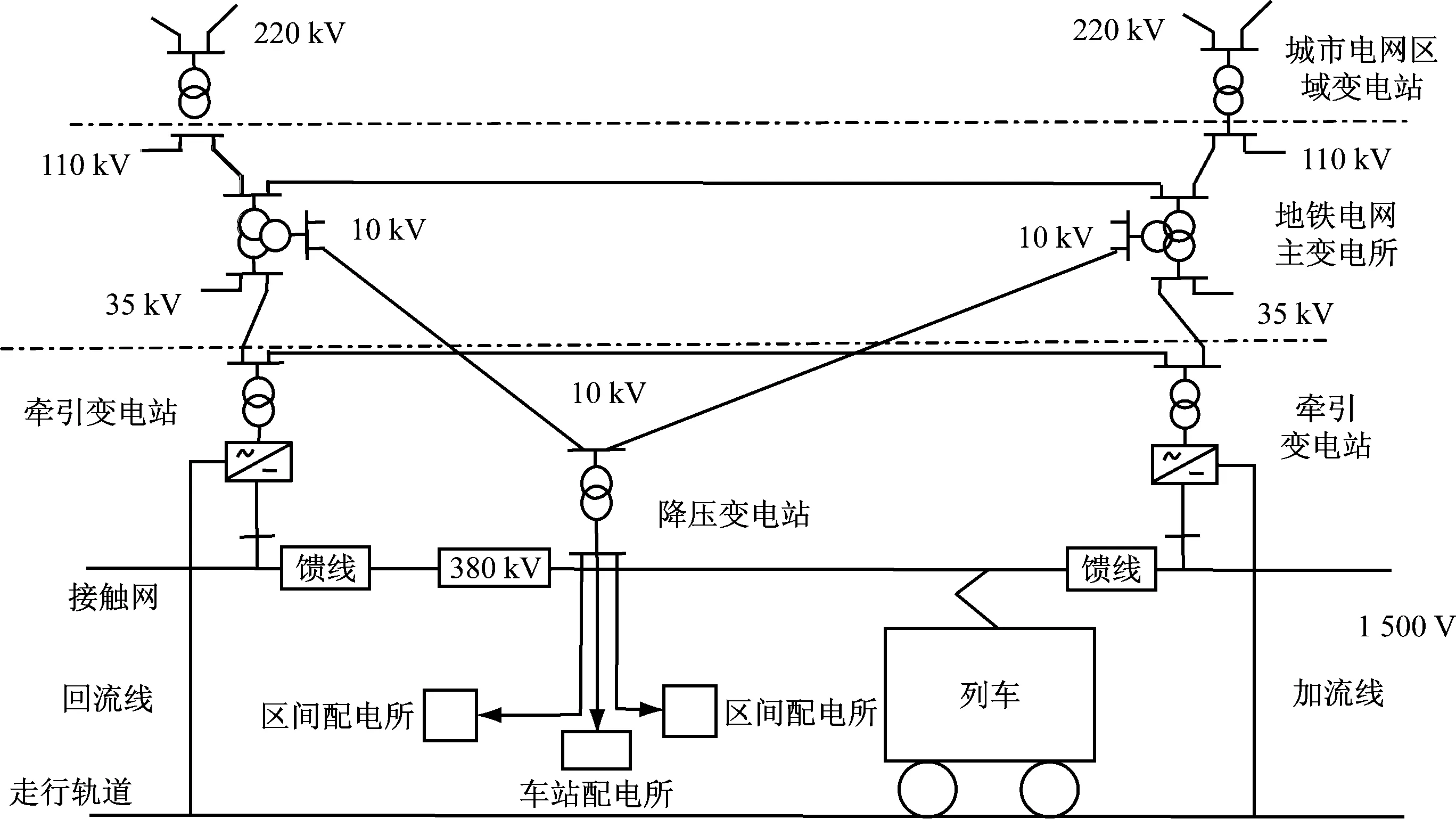
图1 地铁牵引供电系统组成示意图

表1 地铁牵引供电系统常见故障现象与原因统计
3 地铁牵引供电系统失效故障树分析
3.1 定性分析
本文采用行列式法求得地铁牵引供电系统失效故障底事件的最小割集。行列式法亦可称为福塞尔法[9-10],其理论根据为:与门使割集容量变多,但不增加割集数目;或门使割集数目增多,但不扩大割集容量。运用行列式法应该从顶事件着手,运用着层代思想,通过布尔代数化简处理,就可得到顶事件的最小割集。
对故障树模型进行计算,得到29个底事件最小割集,分别为:X1,X2,X4,X5,X6,X9,X10,X11,X12,X13,X14,X15,X16,X17,X18,X22,X23,X26,X29,X30,X32,X33,X38,X39,(X27,X28),(X34,X36),(X30,X37),(X8,X24,X25),(X19,X20,X21)。
3.2 定量计算
3.2.1 顶事件发生概率
底事件最小割集发生概率为:
第三、银子“有灵说”。在白银古道及其左近区域民间还有许多关于银子“有灵说”的故事。老人家多耳熟能详。大体上说,许多上代财主、大贾发家之后本着财不露眼的原则将一些银子或埋于地下,或藏于墙间,或藏于房间地板之下等等。随着年代的久远,或因主人突然去世而遗忘。但年代久远的银子会变成兔子、羊等动物,晚上出来玩耍,如遇有缘之人,去追由白银变成的兔子或羊,则可得到银子。如上洋村就有此传说,相传,彭八公在煽炼银子时,曾在围城底藏有银子两缸,并在路旁岩壁上刻着:“银藏围城底,弗是在山冈;孰会猜得中,拾银两大缸。”古往今来,这两缸银子藏在何方?无人猜得中。
(1)
式中:
xj——底事件最小割集,j=1,2,…,n;其中,n为最小割集阶数;
Pj——底事件最小割集xj发生的概率。
则顶事件发生的概率为:
PT=F(y1∩y1…∩yk)
(2)
式中:
yi——事件Yi的最小割集,i=1,2,…,n;
k——最小割集阶数。
当Y1,Y2,…,Yk为独立事件时,有
(3)
式中:
Fi——事件i阶最小割集发生的概率。
从而可得到系统平均无故障运行时间为:
(4)
由式(1)、(2)、(3),以及表3计算可得地铁牵引供电系统的不可靠度,即地铁牵引供电系统失效事件(顶事件)的发生概率为0.008 169 855/d,故

表2 地铁牵引供电失效故障的底事件及其发生概率
TM=122.401 191 854 d。
3.2.2 底事件重要度
在地铁牵引供电系统失效故障树模型中包含众多底事件,但这些底事件对顶事件的重要性各不相同,即底事件的重要度不同。通常将底事件重要度分为结构重要度和概率重要度。
结构重要度为
(5)
式中:
Jj——底事件Xj的结构重要度近似值;
n——底事件Xj所在最小割集yi的阶数。
概率重要度Ij为底事件Xj发生概率变化对改变顶事件发生概率的影响水平。其计算公式为:

a) 地铁牵引供电系统失效故障树b) 受电弓失效故障树c) 基础网失效故障树d) 环网电缆失效故障树e) 主变电所失效故障树f) 接触网悬挂失效故障
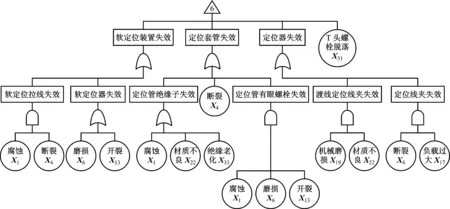
g) 定位装置失效故障树

h) 拉弧故障树i) 接触网失效故障树j) 馈线失效故障树
图2 地铁牵引供电系统失效故障树模型
(6)
由式(5)计算,可得地铁牵引供电系统失效底事件最小割集的结构重要度,如表3所示。

表3 地铁牵引供电系统失效底事件最小割集结构重要度
由表3可见,腐蚀、疲劳、断裂、磨损、放电等底事件最小割集的结构重要度为1.00。这说明只要此类事件发生便会导致地铁牵引供电系统失效。其故障主要集中在受电弓和接触网等关键处。
以底事件最小割集阶数n作为自变量,以底事件最小割集结构重要度Jj作为因变量,得到二者关系如图3所示。

图3 底事件最小割集阶数与其结构重要度关系
由图3可见,n越大,Jj越低。这说明n对Jj影响比较大。由式(5)与图3可知,Jj主要是从故障树结构角度的分析,与底事件发生概率无关。
由式(6)计算可得地铁牵引供电系统失效底事件的概率重要度,如表4所示。
由表4可见:X4(断裂)、X6(磨损)、X10(放电)及X11(闪络)等事件的概率重要度最大,对地铁牵引供电系统失效影响最大;天气严寒、驰度小、脱落、电弧、载流量小等事件的概率重要度比较大,对地铁牵引供电系统失效影响也比较大;化学磨损、电气磨损、张力小等事件的概率重要度较小,对地铁牵引供电系统影响较小[2-3]。此外,概率重要度大的底事件为主要集中在受电弓和接触网等关键节点处发生的故障。这类故障主要会导致地铁牵引供电系统发生断路故障。
分别以底事件X6(磨损)、X10(放电)及X24(波动速度小)的发生概率作为自变量,以地铁牵引供电系统可靠度为因变量,得到关系曲线如图4所示。
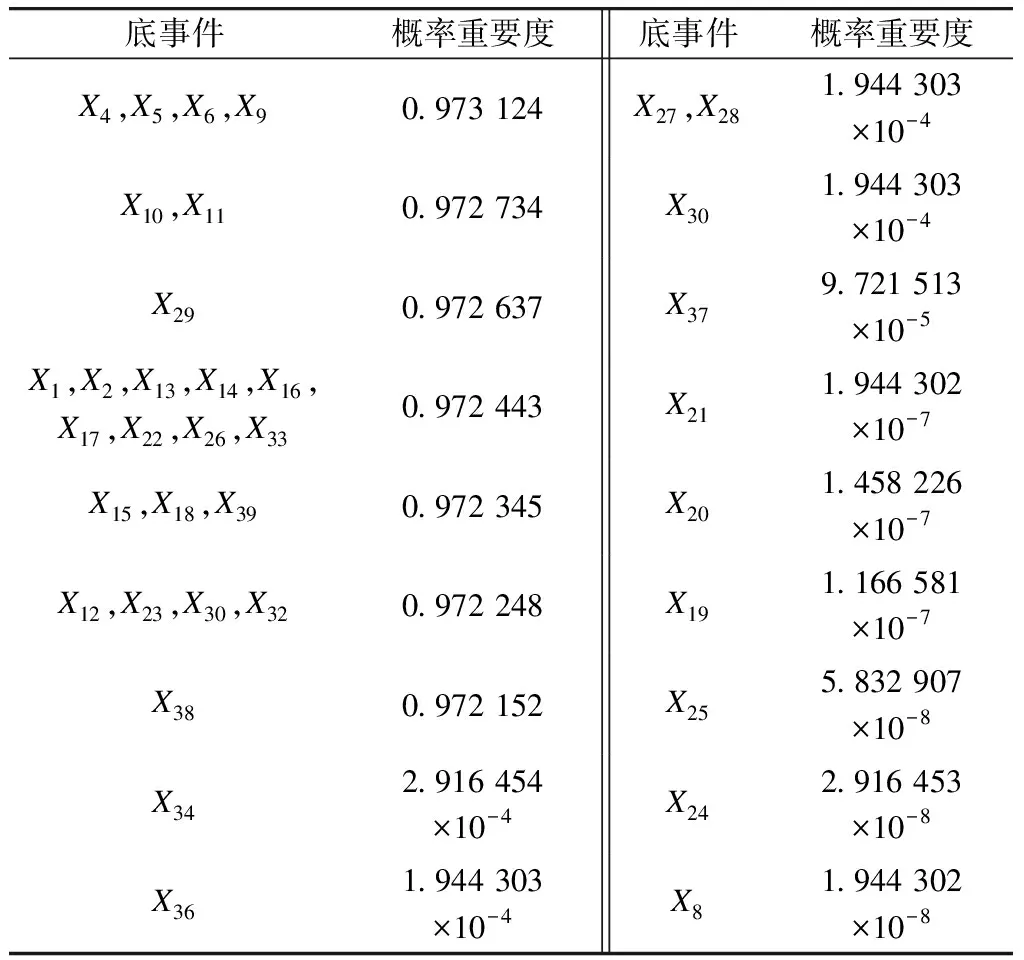
表4 地铁牵引供电系统失效底事件的概率重要度
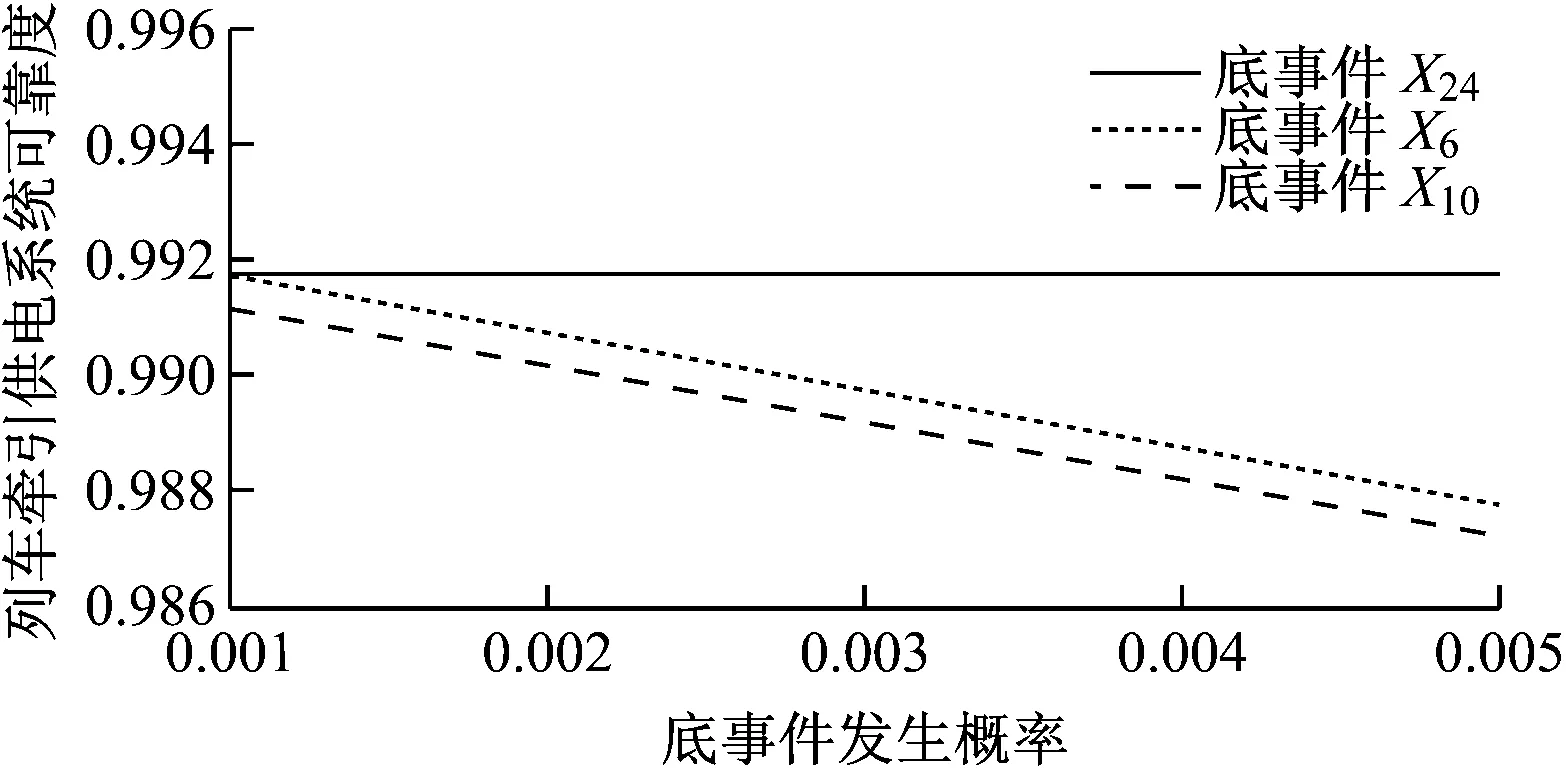
图4 底事件发生概率对地铁牵引供电系统可靠度影响
由图4可见,当X6、X10发生概率增大时,地铁牵引供电系统的可靠度逐渐降低。这说明X6及X10对地铁牵引供电系统可靠度有重大影响。但X24发生概率增大时,地铁牵引供电系统可靠度没有明显变化。这说明X24对地铁牵引供电系统可靠度的影响不大[7]。综上所述,包含在最小割集中的底事件对地铁牵引供电系统可靠度的影响,随着底事件的发生概率不同而不同。
4 结语
本文建立了地铁牵引供电失效的故障树模型。通过定性分析相关可靠性指标,找出地铁故障树模型的29个最小割集。通过定量计算得到,地铁牵引供电系统可靠度为0.991 83,平均无故障运营时间为122.401 191 854 d。通过计算并分析底事件的结构重要度和概率重要度发现,底事件的结构重要度与底事件发生概率无关,结构重要度与底事件所在最小割集阶数有关,阶数越高底事件结构重要度越低;而且,底事件发生概率越大,地铁牵引供电系统可靠度越低。但不在最小割集中的底事件发生概率不影响牵引供电系统可靠性。
通过分析地铁牵引供电失效故障树模型底事件结构重要度和概率重要度发现,重要度最大的底事件为断裂、磨损及放电,且相应故障主要集中发生在受电弓和接触网的关键节点处。因此,应加强对受电弓和接触网关键节点的维护与检测。

