基于点基局部光滑点插值法的结构动力分析

张桂勇， 鲁 欢， 王海英， 于大鹏， 孙铁志

(1.大连理工大学 船舶工程学院 辽宁省深海浮动结构工程实验室，大连 116024；2.大连理工大学工业装备与结构分析国家重点实验室，大连 116024；3.高新船舶与深海开发装备协同创新中心，上海 200240；4.大连海洋大学 航海与船舶工程学院，大连 116023)

经过半个世纪的发展，有限元法已成为科学研究以及工程应用方面强有力的数值工具，并拥有诸多的商业软件，能够对各类复杂物理问题进行分析求解，但其同时也存在一些固有缺陷：其中之一就是三角形单元(四面体)网格划分简便，但其刚度过硬，导致计算精度较差和收敛性不佳；四边形(六面体)单元精度高但难以实现复杂构件的网格自动剖分。

为了克服有限元法的缺陷，国内外学者进行了大量的研究。Pian等[1]提出了混合有限元法以改善传统有限元法的计算性能；Liu等[2-4]在提出G空间理论和广义梯度光滑技术的基础上，进一步提出了无网格光滑点插值法(S-PIM)，点基光滑点插值法(NS-PIM)就是其中的一种。研究发现点基光滑点插值法具有诸多良好的性质：应力/应变解准确，避免剪切锁死，更为重要的是其能给出能量解的上界。已知有限元结果能够提供能量解下界，通过点基光滑点插值法获得能量解上界，从而允许我们从数值角度获得复杂问题能量范数的精确解区间[5-6]。

但点基光滑点插值法有其自身缺陷，表现为刚度“过软”[7-8]。研究发现：其在动力学求解时，常会出现虚假的非零能模式；尽管采用无条件收敛的直接积分法如Newmark法[9]，时间也会不稳定[10-11]；且在求解固有频率时，常常会出现计算结果偏低，在高阶频率时表现尤为明显。

针对点基光滑点插值法的上述缺陷，本文将其与有限元法结合，对问题域进行局部应变光滑，借助着有限元法刚度“过硬”特性[12]，来矫正点基光滑点插值法刚度“过软”情况，以期得到接近实际刚度的模型，并改善原始点基光滑点插值法动力求解时的时间不稳定状况。为了验证该方法的有效性，进行了一系列固有频率和响应计算。结果表明本文所提出方法能够有效克服点基光滑点插值法刚度过软造成的虚假非零能模式和固有频率过低的问题，在采用同样线性三角形单元网格对问题域进行离散的情况下，能够给出较有限元模型更为准确的数值结果。

1 数值模型

1.1 有限元法

传统有限元基于如下伽辽金弱形式

(1)

位移场被近似为

(2)

式中:NJ(x)为形函数矩阵;dJ为节点位移矢量;NP为插值所用的节点数。

将式(2)代入式(1)中得到系统的离散方程

KFEMd=f

(3)

式中:KFEM为有限元系统刚阵;f为力矢量，由以下公式得到

(4)

(5)

式中

(6)

本文采用三节点三角形单元，应变矩阵是常数矩阵，则式(4)变为

(7)

式中:Ve为单元面积。

1.2 点基光滑点插值法

点基光滑点插值法借助背景单元对问题域离散，在此基础上形成基于节点的应变光滑域，如图1所示，Ω(K)为节点K所在的光滑域，Γ(K)为光滑域边界。

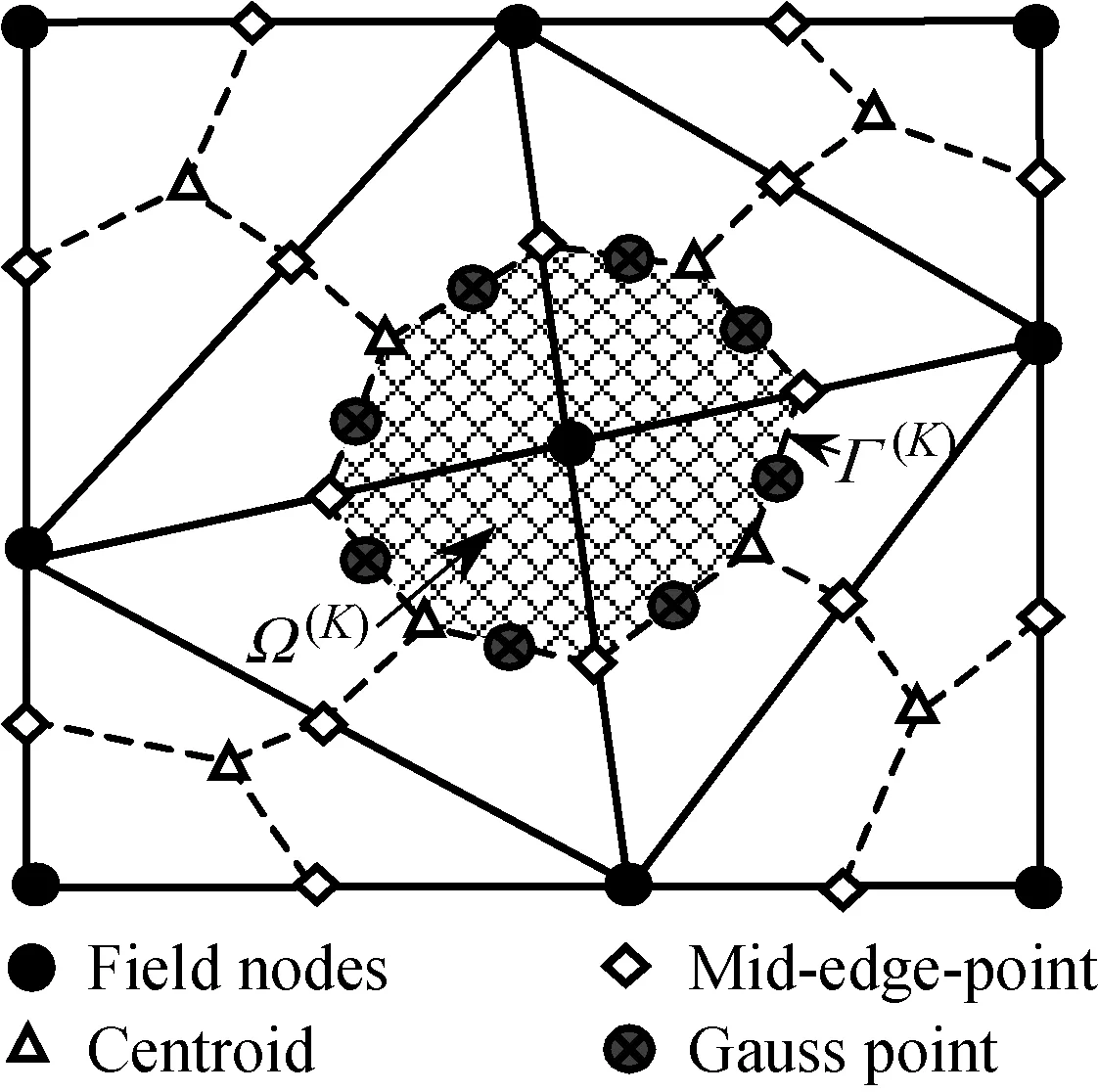
图1 三角形背景网格以及在此基础上形成的基于节点的应变光滑域

Fig.1 Triangular background elements and strain smoothing domains associated with field nodes

根据GS-Galerkin(Generalized smoothed Galerkin weak form)弱式得到下式

(8)

(9)

(10)

式中:n1和n2分别对应光滑域边界的方向余弦。

位移场近似表示为

(11)

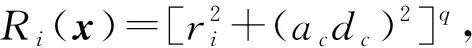
(12)

将式(10)、(11)代入式(9)中得到

(13)

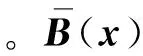
(14)

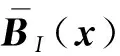
(15)

将式(10)和形函数ΦI(x)代入式(15)中得到

(16)

式中

(17)

式中:nl(x)为Ln矩阵中的元素。采用高斯积分对式(17)计算，得到

(18)

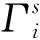
将式(11)、(13)代入式(8)中得到

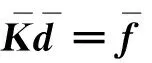
(19)

式中

(20)

(21)

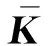
(22)

(23)

1.3 点基局部光滑点插值法求解动力问题

由前面介绍得知，点基光滑点插值法将每个三角形背景网格分为三部分，参与以对应节点为中心的梯度光滑过程，并且前面的研究已经证明此方法刚度过软；而有限元法则可看作每个背景单元均未进行梯度光滑过程，其刚度过硬。综合以上两种方法的特点，如图2所示，本文方法把背景单元的每条边三等分，每个等分点分别连接相邻两边最近的等分点，将背景单元分割为顶点处三个三角形区域和中间空白六边形区域。其中三个三角形区域(图2中阴影部分)参与形成对应节点光滑域，而中间的六边形区域则不进行梯度光滑，因此方法可以看作是基于点的局部梯度光滑点插值法。

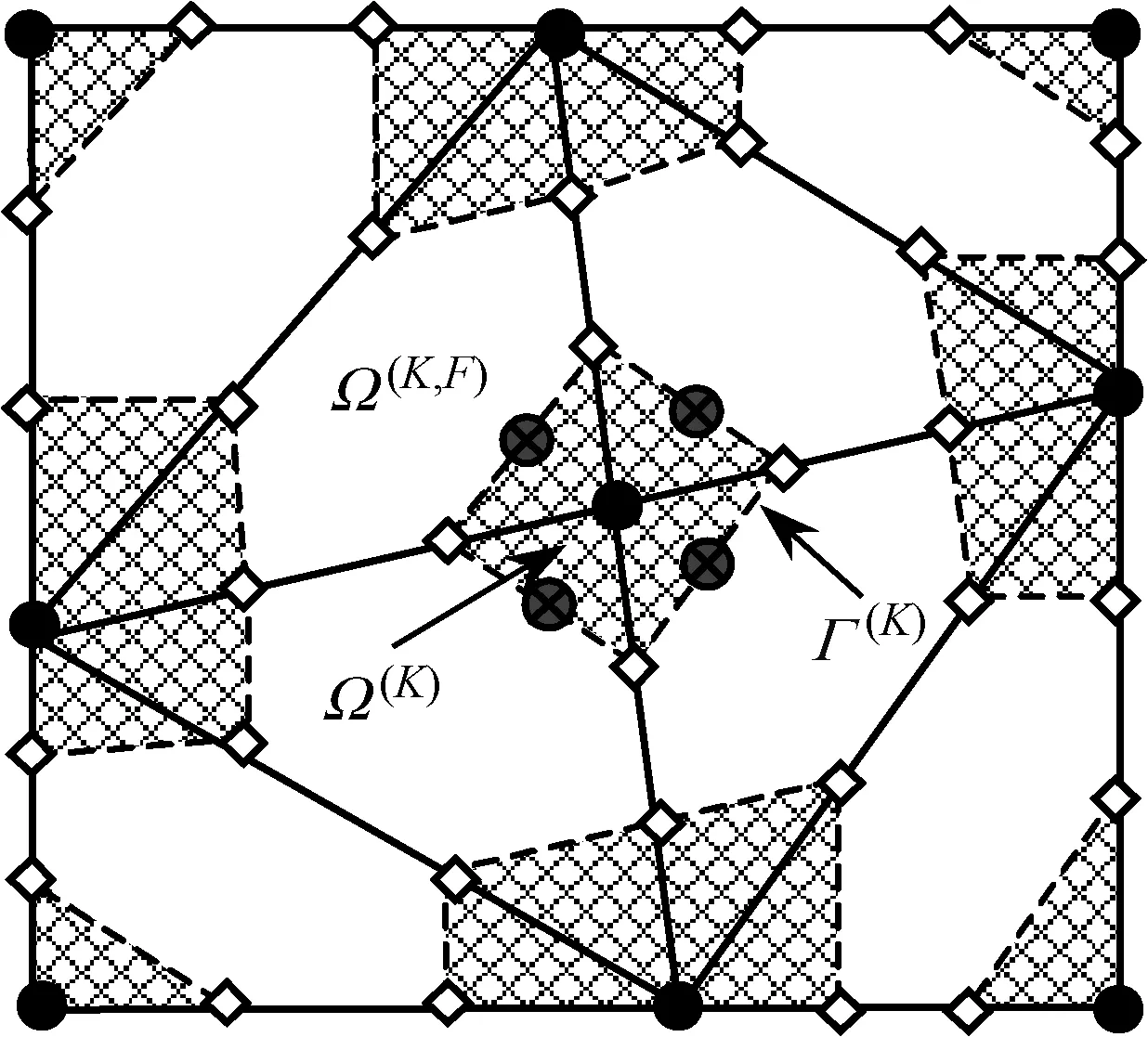
图2 点基局部光滑点插值法问题域背景网格及光滑域形成

Fig.2 Background elements and smoothing domains of the NPS-PIM

对于动力问题GS-Galerkin弱式可写为

(24)

式中:ρ为质量密度。

将各个物理量代入式(24)得到

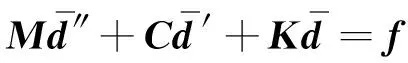
(25)

此式为动力学求解的一般形式，其中，M为质量矩阵，C为阻尼矩阵，f为力矢量，因此，只要得到各个矩阵，求解便可以得到固有频率值和响应值，本文点基局部光滑点插值法的刚度阵是将有限元法和点基光滑点插值法的二者的刚度阵结合，刚度阵K的求解如下

(26)

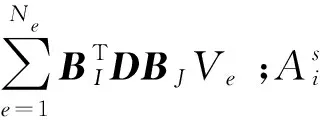
质量阵M采用的是集中质量阵，是将每个单元的质量平均地分配给该单元的节点，对所有单元循环组装得到总的质量阵。

对于自由振动，不考虑外力和阻尼，因此式(25)简化为

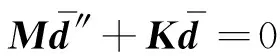
(27)

求解该式有时需要施加边界条件，大多为本质边界，本文计算采用消去法，直接将边界条件节点对应的刚度阵和质量阵处的元素划去。式(27)的解可表示为

(28)

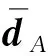
(29)

对于受迫振动，需要考虑阻尼的影响并施加外力，本文中的阻尼采用瑞利阻尼

C=αM+βK

(30)

式中:α,β为阻尼系数。

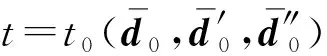
(31)

(32)

(33)

1.4 数值实现

点基局部光滑点插值法求解自由振动问题时数值流程如下：

1) 对节点光滑域循环。

2) 对光滑域中的单元循环。

3) 对单元中光滑域边的高斯点循环。

(a) 根据节点选择方案选择插值节点并计算点插值函数。

(b) 计算应变位移矩阵。

(c) 计算节点刚度阵及力矢量。

(d) 将节点刚度阵及力矢量组装到整体刚阵及整体力矢量。

4) 结束高斯点循环。

5) 结束单元循环。

6) 结束节点光滑域循环。

7) 对单元循环。

(a) 计算单元梯度矩阵B。

(b) 计算单元刚度阵、质量阵以及力矢量。

(c) 将单元刚度阵、质量阵以及力矢量组装。

8) 结束单元循环。

9) 将有限元和点基光滑点插值法的总刚叠加，得到最终的刚度矩阵。

10) 施加本质边界条件。

11) 根据最终刚度阵和质量阵求解得到各阶固有频率。

2 分片试验

检验一个数值方法是否收敛于真实解可利用分片试验，其要求内部与边界的节点位移满足相同的线性函数[13](机器误差范围内)。

如图3所示，这里利用132个节点离散该方片，以探究本文方法是否收敛于真实解，加载边界处的线性位移为

(34)

上述位移亦为方片的解析解。利用位移误差范数来检验位移误差，如下式

(35)

式中，上标“nume” 表示数值解，上标“exact”表示解析解，Nn为总的节点数。计算得到本文方法的上述位移误差范数为0.122 5×10-14，证明了该方法能够通过分片试验。

3 数值算例

3.1 细长悬臂板的自由振动

本节将研究细长悬臂板的自由振动，其尺寸为：长L=100 m，宽D=10 m，厚度t=1.0 m，杨氏模量2.1×104Pa，泊松比v=0.3，质量密度ρ=8.0×10-10kg/m3。利用三种不同的网格划分离散该问题域，分别为：274，612，和1 104个不规则节点。由于欧拉理论悬臂梁解析解未考虑剪切变形的影响，所以本文利用精细网格划分100×10的FEM-Q4单元求解该问题得到的解作为参考解[14]。

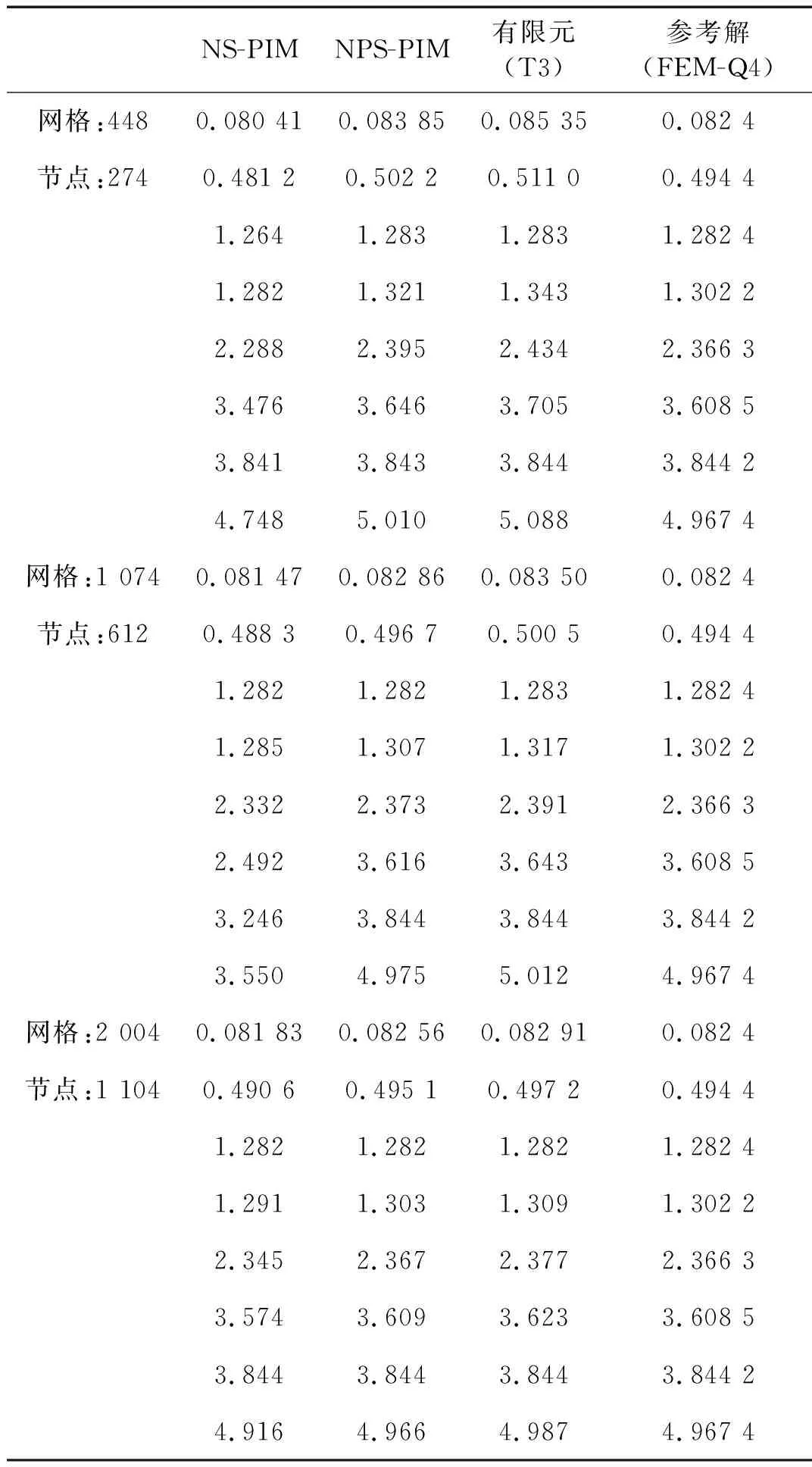
表1列举了采用相同节点离散、不同方法求得的该悬臂板的前八阶固有频率值，图4给出了前八阶模态。根据数据结果可知，当前的NPS-PIM方法求得的

表1细长悬臂梁前八阶固有频率(10kHz)

Tab.1Firsteightnaturalfrequencies(in10kHz)oftheslendercantilever

NS-PIM NPS-PIM 有限元(T3) 参考解(FEM-Q4)网格:448 0.080 41 0.083 85 0.085 35 0.082 4节点:274 0.481 2 0.502 2 0.511 0 0.494 4 1.264 1.283 1.283 1.282 4 1.282 1.321 1.343 1.302 2 2.288 2.395 2.434 2.366 3 3.476 3.646 3.705 3.608 5 3.841 3.843 3.844 3.844 2 4.748 5.010 5.088 4.967 4网格:1 074 0.081 47 0.082 86 0.083 50 0.082 4节点:612 0.488 3 0.496 7 0.500 5 0.494 4 1.282 1.282 1.283 1.282 4 1.285 1.307 1.317 1.302 2 2.332 2.373 2.391 2.366 3 2.492 3.616 3.643 3.608 5 3.246 3.844 3.844 3.844 2 3.550 4.975 5.012 4.967 4网格:2 004 0.081 83 0.082 56 0.082 91 0.082 4 节点:1 104 0.490 6 0.495 1 0.497 2 0.494 4 1.2821.2821.2821.282 4 1.2911.3031.3091.302 2 2.3452.3672.3772.366 3 3.5743.6093.6233.608 5 3.8443.8443.8443.844 2 4.9164.9664.9874.967 4

模态1，f=838.5 Hz

模态2，f=5 022 Hz

模态3,f=12 830 Hz

模态4，f=13 210 Hz

模态5，f=23 950 Hz

模态6，f=36 460 Hz

模态7，f=38 430 Hz

模态8，f=50 100 Hz

图4 NPS-PIM方法求得的悬臂板前八阶振动模态

Fig.4 First 8 free vibration modes of the slender cantilever by NPS-PIM

固有频率比有限元小，并克服了点基光滑点插值法解固有频率值过低的缺陷，较之二者均更接近真实解，且前八阶模态中没有虚假的非零能模态出现，时间稳定。

3.2 剪切墙的自由振动

如图5所示，该算例将研究有四个开口的剪切墙，墙底部完全固定，计算状态为平面应力。利用522个不规则节点离散该问题域。基本数据为E=1.0×104Pa，v=0.2，t=1.0 m，ρ=1.0 kg/m3。

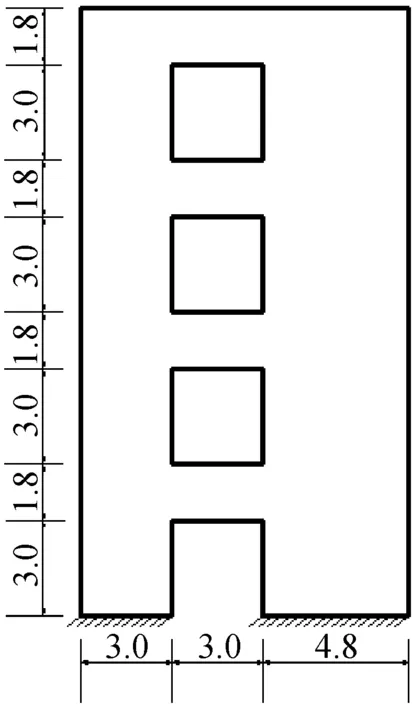
图5 带有四个开口的剪切墙及背景网格划分Fig.5 A shear wall with four openings and its background meshes

在相同节点离散下、用不同方法求得的前八阶固有频率列于表2中，相应地用本文方法求得的模态绘于图6中。从结果中可知，在相同的节点离散下，较之有限元法(T3)，本文提出的NPS-PIM方法其结果和参考解更加接近；与点基光滑点插值方法相比，克服了其求解固有频率值过低的缺陷，更接近参考解。并由图6可以看出NPS-PIM计算得到的前八阶阵型并未出现虚假的非零能模态，克服了原始点基光滑点插值法的时间不稳定性。

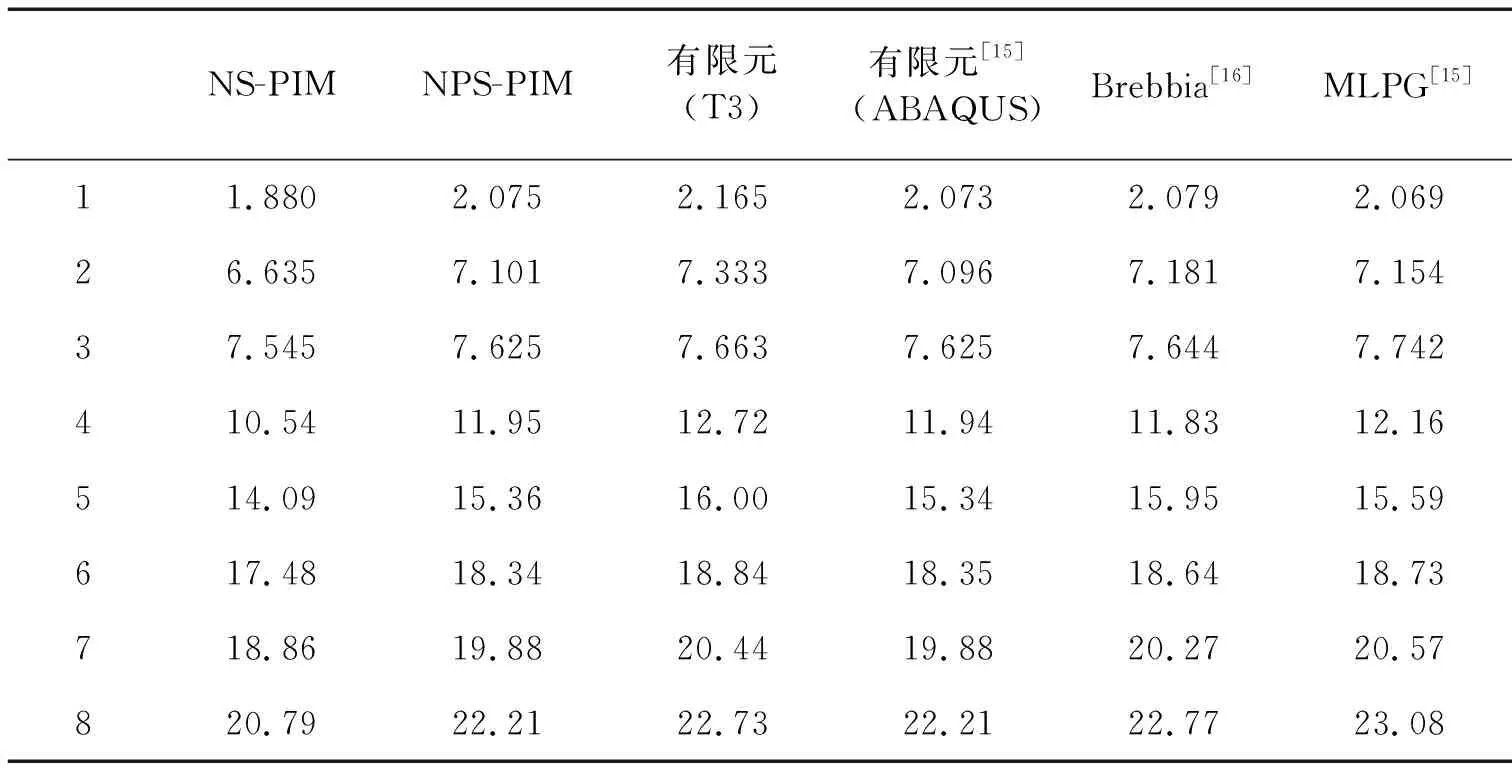
表2 剪切墙的前八阶固有频率Tab.2 First eight frequencies(rad/s) of a shear wall rad/s

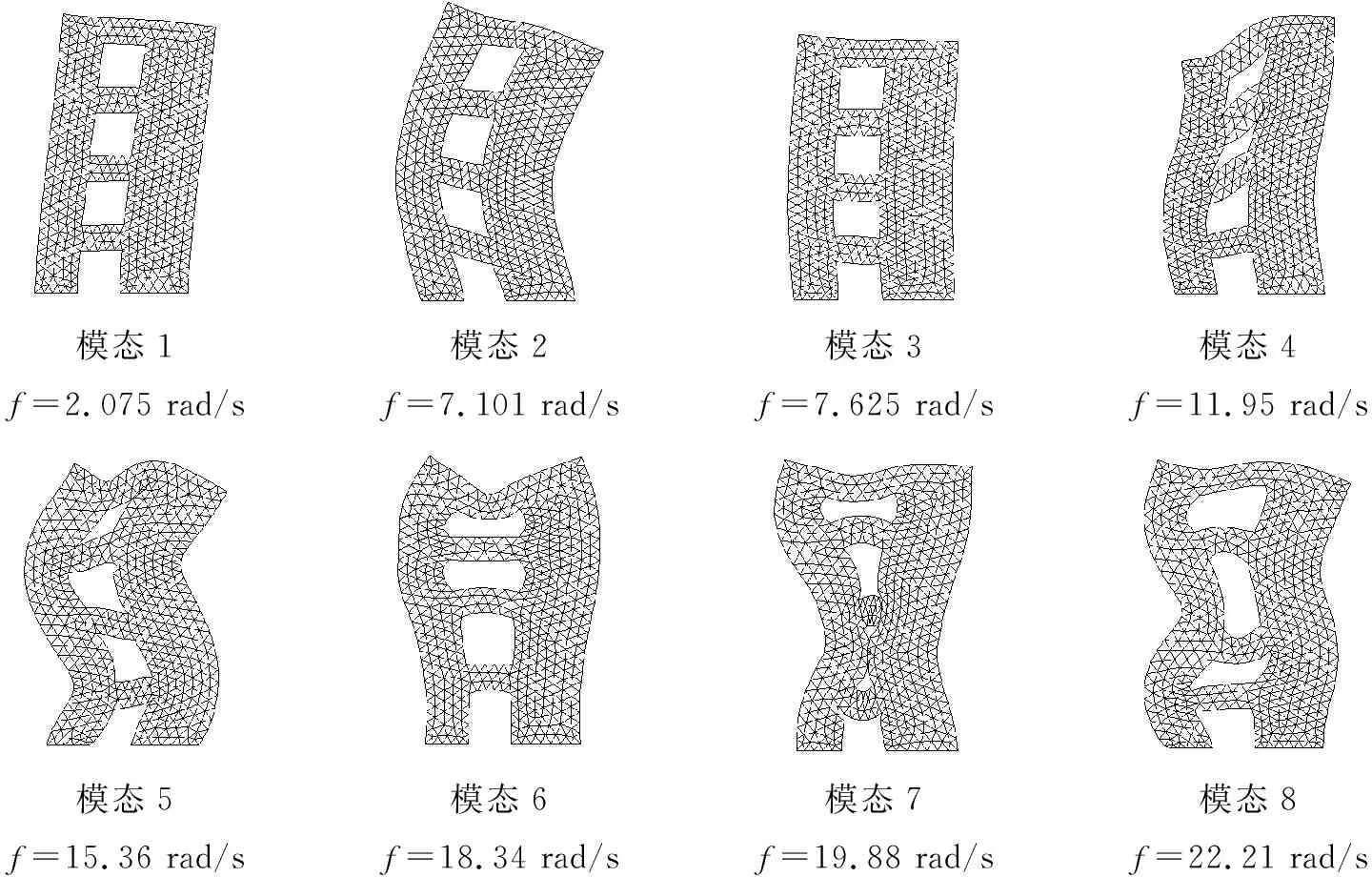
模态1f=2.075 rad/s模态2f=7.101 rad/s模态3f=7.625 rad/s模态4f=11.95 rad/s模态5f=15.36 rad/s模态6f=18.34 rad/s模态7f=19.88 rad/s模态8f=22.21 rad/s

图6 NPS-PIM求得的剪切墙的前八阶模态

Fig.6 First 8 free vibration modes of the shear wall by the NPS-PIM

3.3 端部施加简谐载荷的细长悬臂板的受迫振动

如图7所示，受迫振动的算例是一个悬臂板，计算状态为平面应力状态。其基本数据为：杨氏模量E=3×107Pa，泊松比v=0.3，厚度t=1.0 m，时间间隔Δt=1×10-3s。该算例中，悬臂板端部受到一个简谐载荷P=1 000g(t)。计算时，利用275个不规则节点离散该问题域。为简单起见，取质量密度ρ=1.0 kg/m3，取悬臂梁端部点A的Y方向位移作为考察。为了比较，利用有限元FEM-T3在相同节点离散下计算该问题，并以有限元FEM-Q4精细网格结果作为参考解。

首先，考虑载荷g(t)=sin(ωft)的情况，其中，ωf=27是载荷的频率。本文采用瑞利阻尼，其两个参数分别为α，β。对于振动方程的求解，这里采用Newmark法，当0.5≤θ≤1，Newmark法无条件稳定，现取θ=0.5。

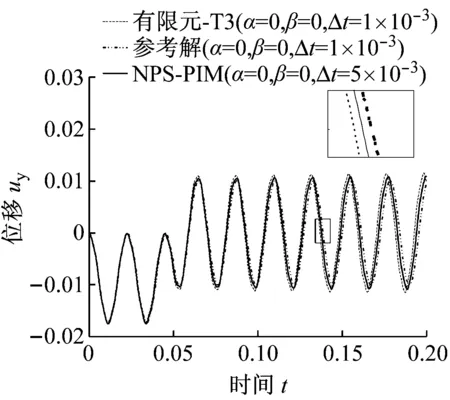
如图8所示，采用相对较大的时间步长Δt=5×10-3s，计算20 s内的位移响应，可以看出，NPS-PIM方法求得的位移响应十分稳定。如图9所示，采用较小的时间步长Δt=1×10-3s，分别计算时程0.2 s和2 s时的响应，从图中可以看出，本文NPS-PIM法比有限元(T3)计算的响应结果更为准确，更接近参考解(有限元Q4)。如图10所示，在无阻尼(α=0,β=0)，悬臂板受到大小为g(t)=1持续时间0.5 s的瞬态载荷时，分别计算了时程为2 s和20 s的响应，从图中可以看出，NPS-PIM求得的瞬态振动的解较有限元精确，在有阻尼的情况下(α=0.000 5，β=0.000 7)求得的响应亦十分稳定。

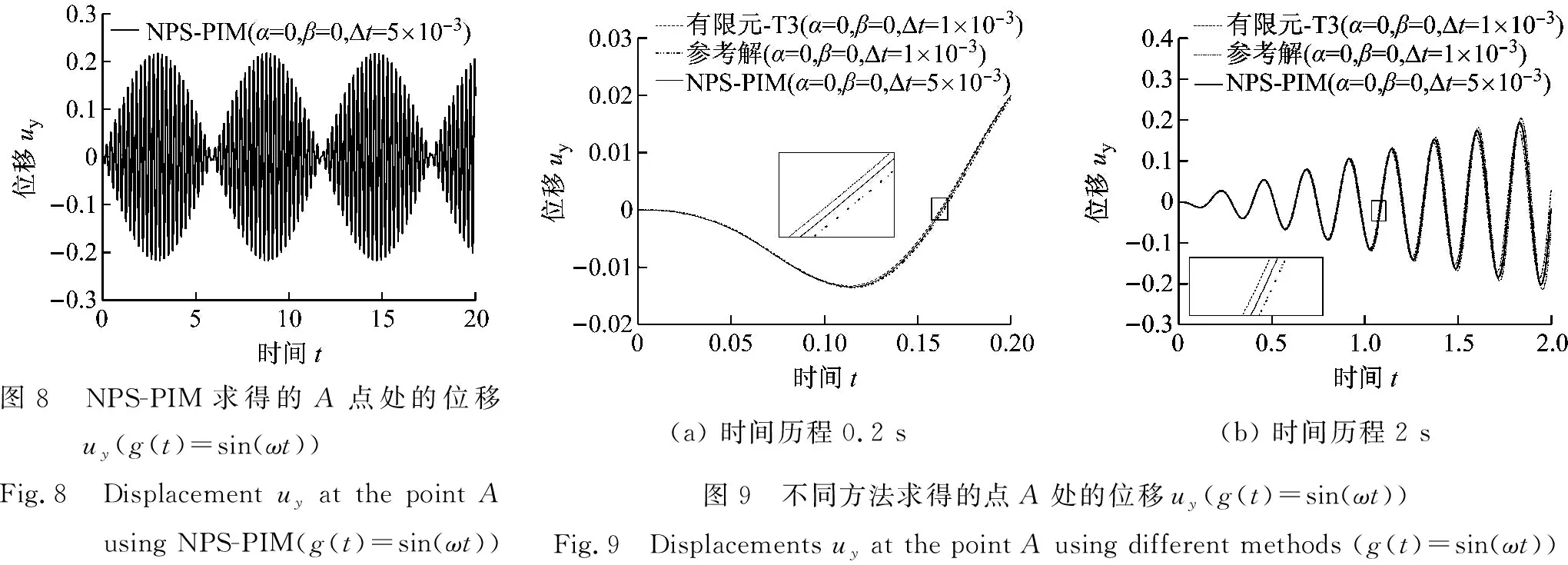
图8 NPS-PIM求得的A点处的位移uy(g(t)=sin(ωt))Fig.8 Displacement uy at the point A using NPS-PIM(g(t)=sin(ωt))(a) 时间历程0.2 s(b) 时间历程2 s图9 不同方法求得的点A处的位移uy(g(t)=sin(ωt))Fig.9 Displacements uy at the point A using different methods (g(t)=sin(ωt))

(a) 无阻尼

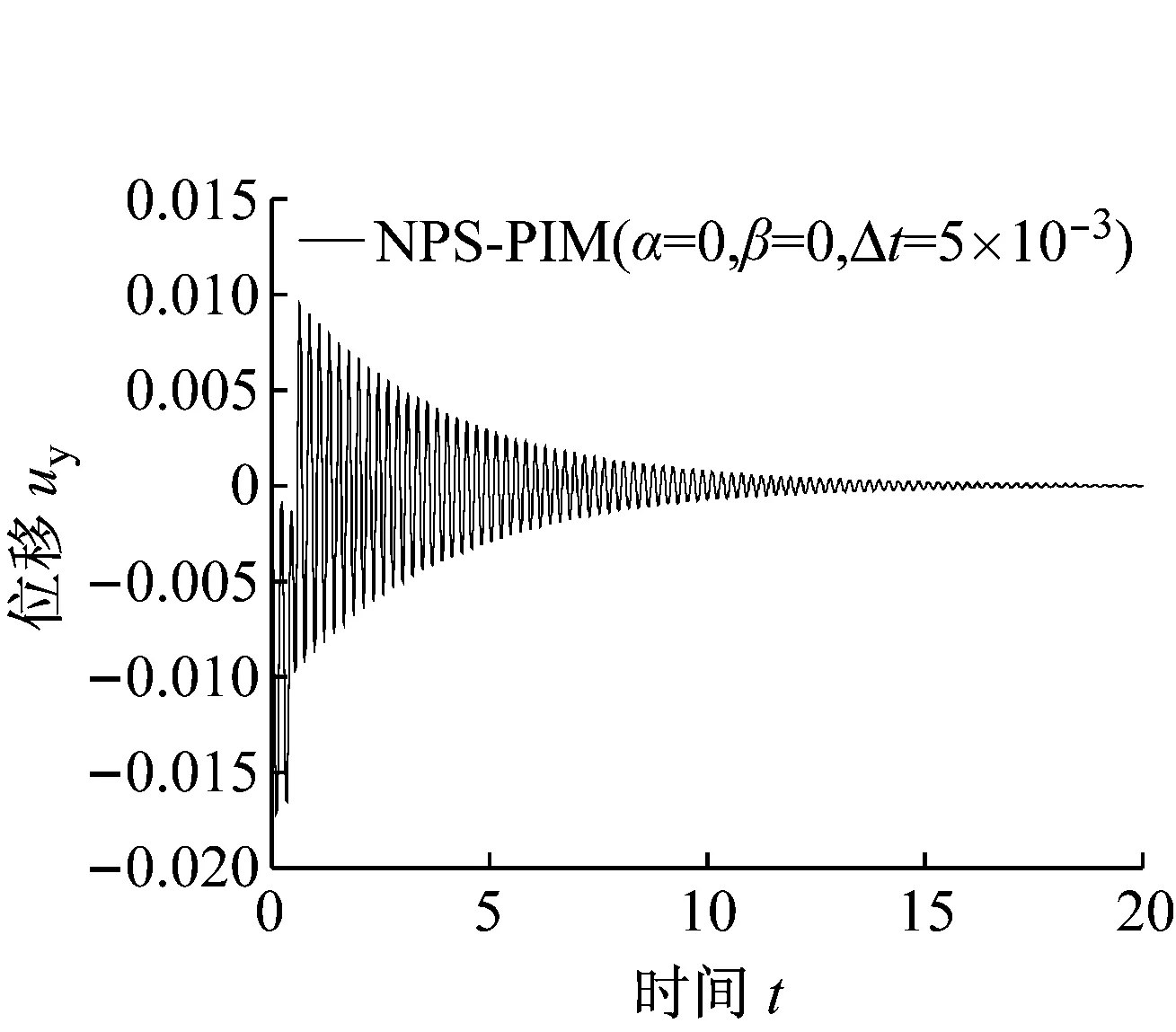
(b) 在有阻尼的情况下图10 不同的方法求得的A点出的瞬态位移uy(α=0.000 5，β=0.000 7)Fig.10 Transient displacements uy at the point A using different methods (α=0.000 5，β=0.000 7)

4 结 论

本文将有限元法和点基光滑点插值法结合(NPS-PIM)，充分利用有限元法过刚、点基光滑点插值法过软的特性，得到了更接近实际刚度的计算模型，并利用数值算例验证了该方法的准确性。通过这些算例我们可以得到以下结论：

(1)NPS-PIM方法能够通过分片试验，收敛于真实解。

(2)NPS-PIM方法克服了NS-PIM的时间不稳定性，求解动力问题时没有出现虚假的非零能模态，时间稳定。

(3)NPS-PIM方法克服了点基光滑点插值法求解固有频率值过低的缺陷，得到的固有频率值更为接近参考解。

(4)在采用同样线性三角形单元网格对问题域进行离散的情况下，NPS-PIM在求解自由振动以及受迫振动时均较有限元准确，基于能够实现自动剖分的三角形背景网格亦能达到较高精度。