基于膜计算与粒子群算法的盲源分离方法
孙 远, 杨 峰, 郑 晶, 徐茂轩, 裴烁瑾
(1.中国矿业大学(北京) 机电与信息工程学院,北京 100083;2. 中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室,北京 100083)
随着信号处理技术的发展,盲源分离(Blind Source Separation, BSS)又称盲信号分离,得到了越来越广泛的关注与研究。盲源分离是在无法获取源信号和传递函数先验知识的前提下,将混合后的各源信号分离出来的过程。它主要广泛应用于医学信号处理、经济指标、语音信号识别,图像处理、地震信号勘测以及通信信号处理等方面[1]。盲源分离中较为常用的假设是源信号的统计独立性,当各个分量零均值且方差为1即相互独立时,就称为独立成分分析(Independent Component Analysis, ICA)[2]。
ICA的目的是从混合后的多路观测信号中,将混合前的源信号分离出来。例如在嘈杂的环境中提取出关心的某些声音、多个传感器记录的脑电波、机械振动信号的分析与降噪等。ICA实质是一种在某一判据条件下的寻优计算,因此,ICA在分离信号的过程中主要进行优化判据和寻优算法两方面工作。在ICA寻优算法的选取上,较为传统的方法是梯度法,梯度法容易受步长以及初值的影响,导致收敛速度较慢。针对这一问题,近些年有关群智能优化算法被广泛的应用与ICA的寻优算法中。文献[3]将粒子群优化算法(Particle Swarm Optimization, PSO)应用到ICA中,较好的识别出滚动轴承故障的类型。然而粒子群优化算法存在早熟收敛的缺点,粒子在全局搜索过程中遇到最优值后容易陷入局部最优值。文献[4]将人工蜂群算法(Artificial Bee Colony, ABC)应用到BSS中,成功的将混合信号分离开来,加快了收敛速度。但该算法含有较多参数,参数选取不当容易导致算法陷入局部极值点,降低分离效果。文献[5]将模拟退火算法(Simulated Annealing Algorithm, SAA)与ICA相结合,提高了ICA的稳态性能。但模拟退火算法的初始温度参数设置较难控制,当初始温度设置较大时,ICA算法需要消耗大量时间,当初始温度设置较小时,则会影响全局搜索能力。文献[6]将遗传算法(Genetic Algorithm, GA)作为ICA的优化算法,有效的分离了非高斯源信号。但遗传算法局部搜索能力较弱,并且实现效果取决于问题的多种参数。
为了解决算法的早熟收敛、参数复杂、分离精度不高的问题,提出一种基于膜计算与粒子群算法的盲源分离方法,可以保证PSO算法局部搜索的精度,满足全局搜索的多样性,并且能避免PSO算法的早熟收敛问题,提高收敛速度和分离性能。
1 独立成分分析原理
线性瞬时混叠ICA模型的原理图,如图1所示。
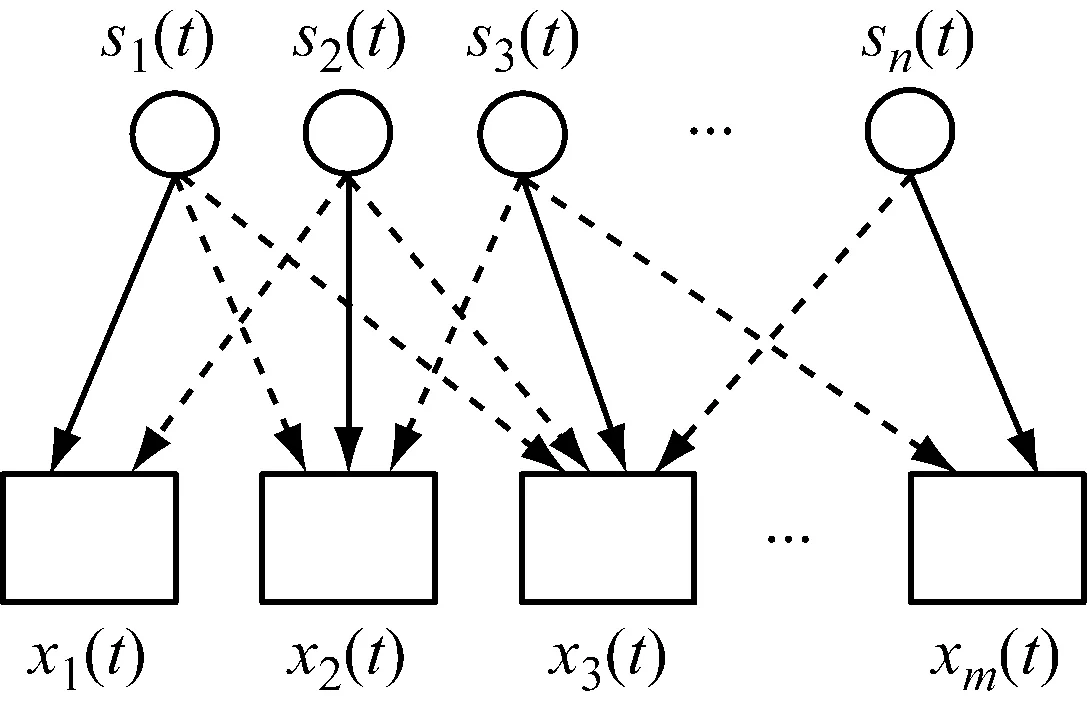
图1 线性瞬时混叠ICA模型的原理图Fig.1 Principle of linear instantaneous mixing ICA model
图1中,s1(t),s2(t),…,sn(t)表示n个源信号,x1(t),x2(t),…,xm(t)表示n个源信号经过线性混合后由m个传感器所接收到的观测信号在t时间的幅值,线性方程表达式如下
(1)
式中:aij(i=1,2,…,m,j=1,2,…,n)是理想状态下xi(t)与si(t)之间的混合参数。
ICA的简单模型如图2所示。
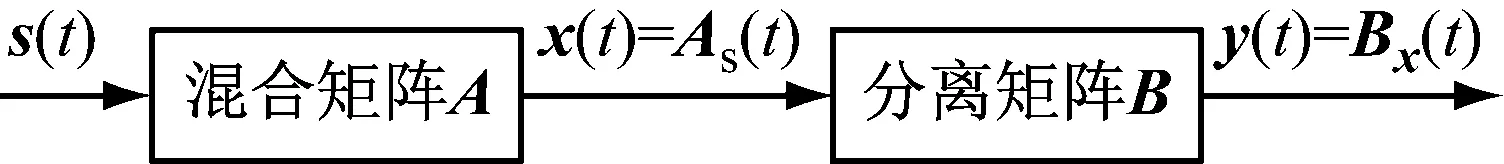
图2 ICA简单模型
Fig.2 Simple model of ICA
图2中,s(t)=[s1(t),s2(t),…,sn(t)]T代表没有先验知识的源信号所组成的N维向量;A是M×N阶混合矩阵;x(t)=[x1(t),x2(t),…,xm(t)]T即为M维观测量;B是分离矩阵,y(t)=[y1(t),y2(t),…,yn(t)]T是传感器接收到的观测信号经过B分离后得到的输出量。ICA要解决的问题就是,在s(t)和A不具备先验知识的情况下,通过对分离矩阵B的求解与更新,得到输出信号y(t),尽量保证y(t)中每个分量相互独立[7]。此时,可以将输出信号y(t)作为s(t)的有效估计值。
2 粒子群优化算法
粒子群优化算法是一种进化计算技术(Evolutionary Computing),主要依靠各粒子之间的相互协作来完成对最优解的寻找。在寻找最优解的过程中,每个粒子根据与目标函数相关的适应值(Fitness Value)对自己当前位置进行评价,找到自己在寻优过程中经历的最好位置pbest,作为粒子的局部最优值。另外,还需要根据计算适应值找到所有粒子在寻优过程中的群体最优位置,即所有粒子发现的最好位置gbest(gbest是pbest中最好的值)。将此群体最优值作为所有粒子的经验,根据式(2)、(3)来更新粒子的速度和位置。
vij(t+1)=wvij(t)+c1rand1(pij-xij)+
c2rand2(gij-xij)
(2)
xij(t+1)=xij(t)+vij(t+1)
(3)
式(2)、(3)中:i=1,2,…,N是粒子群的总数;j=1,2,…,D是种群搜索空间的维数;xij表示第i个粒子第j维分量的位置;vij表示第i个粒子第j维分量的速度;w为惯性权重;c1和c2是学习因子;rand1和rand2是介于(0,1)之间的随机数;pij表示第i个粒子第j维分量当前最好的位置;gij表示所有粒子第j维分量当前最好的位置。在粒子寻优过程中,粒子的速度vi的最大值为Vmax(Vmax>0),如果vi>Vmax,则vi=Vmax。
3 基于MCPSO的ICA算法
从信息论角度讲,信息极大化、互信息极小或极大似然估计均可以作为信号独立性的判据。根据中心极限定理可知,当随机变量X可以由若干相互独立的随机变量Si(i=1,2,…,N)之和表示时,对任意分布的Si,如果Si满足有限的均值和方差这一条件,则Si与X相比,具有更强的非高斯性。因此,在ICA中,可以用非高斯性来衡量输出信号y(t)中各分量的相互独立性,非高斯性越强,表明分离的效果越好。在信息论中,负熵是度量非高斯性的一个较为稳健的判据[8],如式(4)所示
J(y)=HG(y)-H(y)
(4)
根据文献[9]证明,多变量负熵可以近似表示为
(5)
式中:k3表示信号的三阶累积量;k4表示信号的四阶累积量。当信号的概率密度分布对称时,k3=0,则
(6)

(7)
对某一分离矩阵B,J[y]越大,表明对源信号s(t)=[s1(t),s2(t),…,sn(t)]T的分离效果越好。由式(7)可知,寻找J[y]的最大值,对应于PSO算法中寻找fiti的最小值。当用负熵来衡量信号的非高斯程度时,需要满足信号为零均值以及E(yyT)=I(I为单位矩阵)的约束条件。因此,首先需要对信号进行中心化和白化处理,以满足约束条件[11]。
在ICA优化处理过程中,当用梯度法对分离矩阵B进行更新时,基于信息极大化、互信息极小化或极大似然估计目标函数,可以使用如下步长函数[12]
B(k+1)=B(k)+
μk[I-Ψ(y(k))yT(k)]B(k)
(8)
式中:k为更新时的迭代次数;μk>0为时变的调节步长;I为单位矩阵;B(k)为第k次迭代的分离矩阵;Ψ(y(k))为y(k)的非线性奇函数,本文选择为基于皮尔逊系统的分段非线性函数[13]。其表达式如下
(9)
式中:a,b0分别为皮尔逊系统的参数;α3,α4为信号的三阶矩和四阶矩,可以根据矩估计的方法求出。
针对传统的梯度法易受步长影响,导致ICA算法的收敛速度较慢,文献[14]采用粒子群优化算法调整ICA算法的步长μk,根据式(8)更新分离矩阵B,可以减小ICA算法的稳态误差,提高收敛速度。但粒子群优化算法存在着早熟问题,即在迭代更新过程中,粒子会根据当前其它粒子提供的最优位置的经验,均飞向最优位置,忽略其它位置的搜索,此时粒子的飞行速度会大大降低,甚至停止搜索,这导致粒子的全局搜索性能变差,过早的出现收敛。为解决早熟收敛的现象,常采用调节惯性权重w的方法来平衡PSO算法的全局搜索和局部搜索。文献[15]提出线性递减惯性权重策略(LDIW),在粒子进行全局搜索时,w取较大值,使粒子可以在更广的范围进行搜索,在粒子进行局部搜索时,w取较小值,确保粒子能够进行精细化的搜索。为增加迭代初期的全局搜索时间和迭代后期的局部搜索时间。文献[14]提出一种新的非线性递减惯性权重策略(NDIW),解决了PSO的早熟收敛问题。但是,无论LDIW还是NDIW方法,都会增加计算的复杂度,降低ICA算法的收敛速度。考虑到膜计算具有并行处理的特点,可以简化惯性权重的取值问题。因此,提出基于膜计算与粒子群算法(MCPSO)的盲源分离方法。
3.1 MCPSO算法
膜计算是一门基于计算机科学和自然科学的新的计算方法,主要受细胞的启发,并从中提取出计算模型[16]。膜系统主要由膜结构、对象和进化规则三部分构成。膜计算的显著特点在于并行性、分布式和非确定性。
MCPSO算法采用细胞型膜系统的单层膜结构(One Level Membrane Structure, OLMS),其简单结构示意图如图3所示。将粒子均匀地放入若干基本膜中,在每个基本膜内,粒子进行精细化的局部搜索。图4为MCPSO算法膜结构示意图。每个粒子的位置看作是膜区域内的对象。将D维空间的n个粒子均匀的分配到m个基本膜中,表层膜为空。此膜系统的字符表示如下多元组
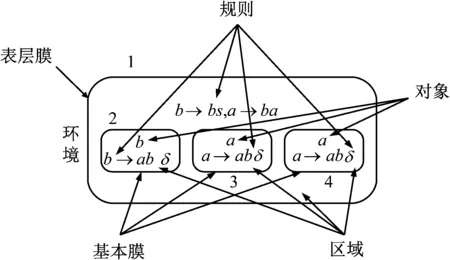
图3 细胞型膜系统结构示意图Fig.3 Cell membrane system structure diagram Π=(V,O,H,μ,w0,…,wm,R0,…,Rm,io)
(10)
式中:V={xij(i=1,2,…,N;j=1,2,…,D)};O⊆V是输出对象的集合;H={0,1,…,m};μ=[[]1[]2[]3…[]m]0;w0,…,wm是对应的膜内的对象多重集;R0,…,Rm表示各膜内区域对应的规则;io是膜系统输出膜的标号。
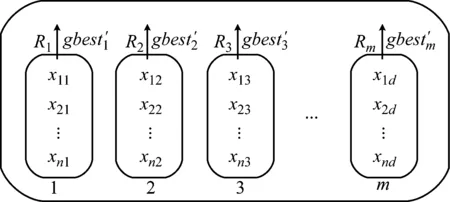
图4 MCPSO膜结构示意图Fig.4 Membrane system structure diagram of MCPSO


图5 MCPSO算法过程示意图Fig.5 Algorithm process diagram of MCPSO
位于m个基本膜内的粒子进行局部搜索,由于膜计算具有并行处理能力,所有基本膜内对粒子最优位置的搜索同时进行,在各基本膜进行局部搜索的同时,对于整个粒子群来说是在进行全局搜索。膜计算的引入,可以提高粒子局部搜索的精度,保证了全局搜索的多样性,避免种群搜索过程中陷入局部最优值。由于MCPSO算法粒子局部搜索和全局搜索同时进行,w只需要取较小值,来确保局部搜索的精度即可,膜计算并行处理的特点,简化了惯性权重w的取值问题,降低了计算的复杂度,提高了PSO算法的收敛速度。
3.2 基于MCPSO的ICA算法流程
基于膜计算和粒子群优化的ICA算法进行信号分离的流程为
步骤1对观测信号进行中心化和白化处理;
步骤2初始化一个单层膜结构,其中包括一个表层膜0和m个基本膜;初始化一个由n个粒子组成的D维空间里按照一定速度飞行的粒子种群,将所有粒子均匀的分配到m个基本膜中,表层膜为空;设定学习因子c1、c2、惯性权重w和最大迭代次数Tmax,随机产生分离矩阵和粒子的飞行速度;
步骤3根据y(t)=Bx(t)计算输出信号y(t),并对y(t)进行中心化和白化处理,根据式(6)、(7)计算各基本膜内粒子的适应度;
步骤4将每个粒子的适应度值与该粒子经过的最好位置pbest做比较,选择适应值较小的粒子作为当前的个体最优位置;将每个粒子的个体最优位置与其所在基本膜内的群体最优位置gbest′做比较,选择适应值较小的粒子作为当前基本膜内群体最优位置;
步骤5将m个基本膜内的群体最优位置通过规则R送至表层膜内,再通过对比此m个群体最优位置,找到适应值最小的一个最优位置gbest,将gbest作为所有粒子的群体最优位置,并将其由表层膜返回至各基本膜;
步骤6根据式(2)、(3)对所有粒子进行速度和位置的更新;
步骤7如果满足终止条件(找到适应度最小的粒子或者达到迭代次数),则停止迭代,输出最优解,否则返回步骤3;
步骤8将步骤7输出的最优解作为式(8)的步长μk,更新分离矩阵B;
步骤9根据y(t)=Bx(t)提取分离信号。
3.3 伪代码
Begin
generation←1
Centralize and sphere observed signal x(t)//中心化、白化观测信号
Initialize skin and elementary membrane structure //初始化表层膜和基本膜结构
Generate n particles in each elementary membrane uniformly//初始化粒子群并均匀分配至基本膜
Initialize separable matrix randomly//随机初始化分离矩阵
Compute output signal y(t) and then centralize and sphere it//计算输出信号并中心化和白化
while(not termination condition) do//终止条件
—Evaluate every particle in each elementary membrane//计算粒子适应度
—Find local best particle pbest //找到粒子个体最优值
—Find local best particle gbest//找到各基本膜内群体最优值
—Execute communication rules//执行膜内规则
—Send global best from all elementary membranes to skin membrane//基本膜内群体最优值送到表层膜
—Chose best value of all received global best as global best among all particles//选择表层膜内最优值作为群体最优值
—Send best value back to each elementary membrane//表层膜内群体最优值送回各基本膜
—Update particle’s velocityV(t)//更新粒子速度
—Update particle’s positionX(t)//更新粒子位置
—generation←generation +1
end
Output best position//输出最优解
Update separable matrixB//更新分离矩阵
Extract separable signal//计算分离信号
end
4 实验结果及分析
4.1 仿真实验
为验证本文提出的MCPSO算法的有效性,实验采用一组正弦波、一组方波、一组锯齿波作为源信号,如图6所示。随机产生线性瞬时混合矩阵A如下,源信号经线性瞬时混合矩阵A混合后的信号如图7所示

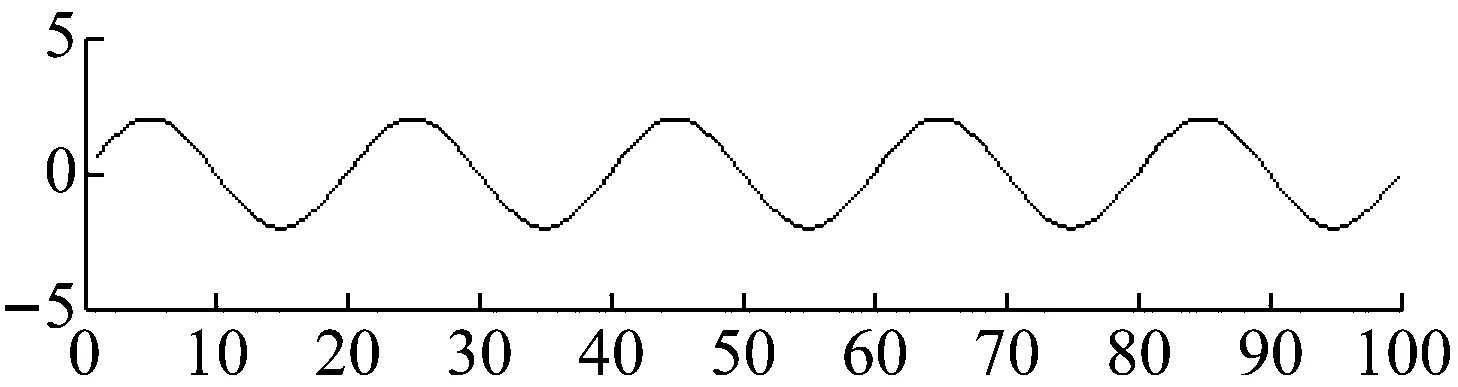
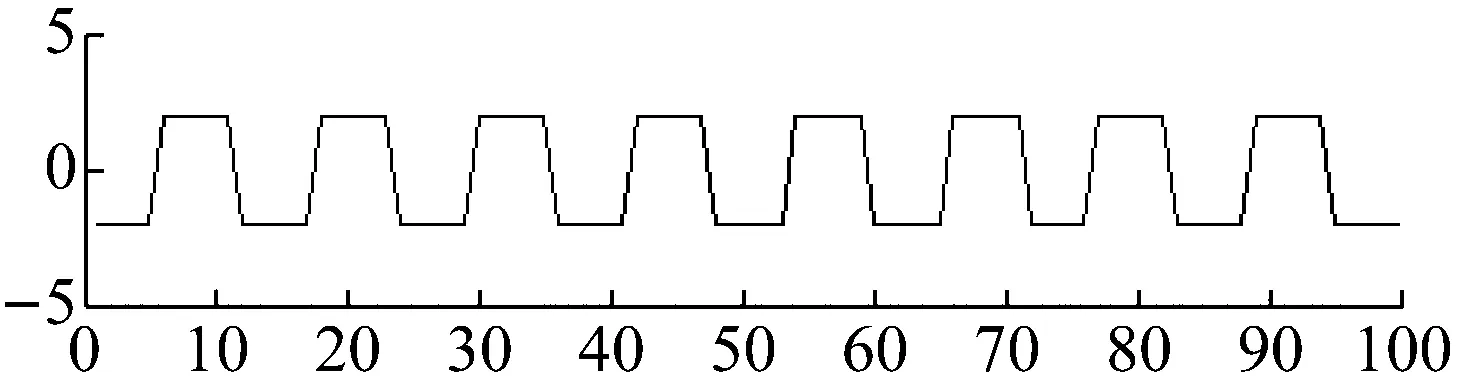
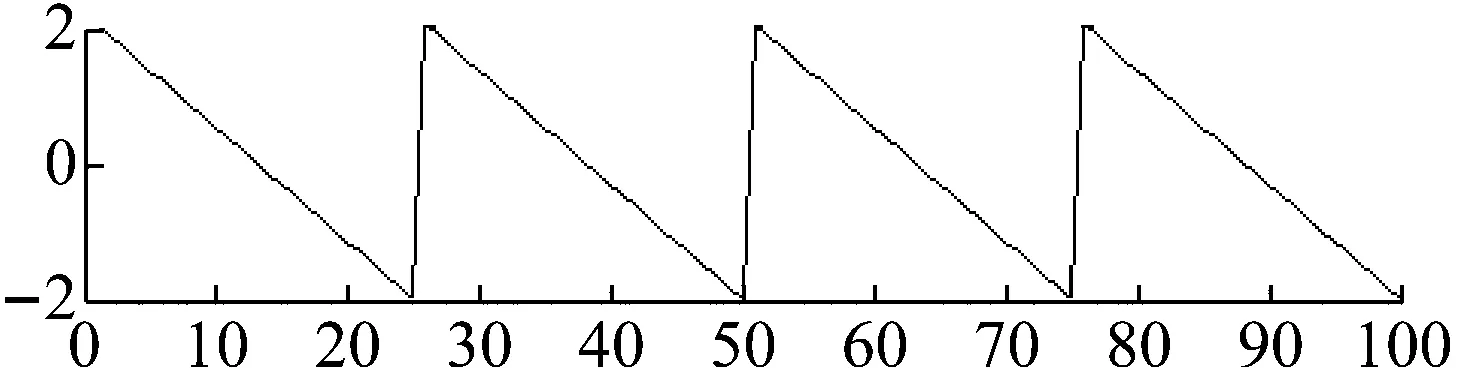
图6 源信号Fig.6 Source signals
仿真实验在MATLAB 2012b下运行,用提出的MCPSO算法和文献[3]中使用线性惯性权重的PSO算法(以下简称线性PSO算法)以及文献[14]中使用非线性惯性权重的PSO算法(以下简称非线性PSO算法)分别对源信号进行分离。MCPSO算法的控制参数为:粒子群个数N=30,搜索空间D=5,基本膜个数m=5,粒子速度范围v=[-1,1],c1=c2=2,惯性权重w=0.4,最大迭代次数Tmax=100。粒子数与基本膜的个数是通过实验对比分析,找到MCPSO算法分离效果最好时对应的粒子数与基本膜个数。分离效果采用相似系数累衡量,其表达式如下
(11)
式中:cov(·)表示方差,si为源信号矢量s中的第i个源信号,yj为经过盲源分离后的与si相对应的分离信号。相似系数越接近1,源信号与分离信号越接近,分离效果越好。

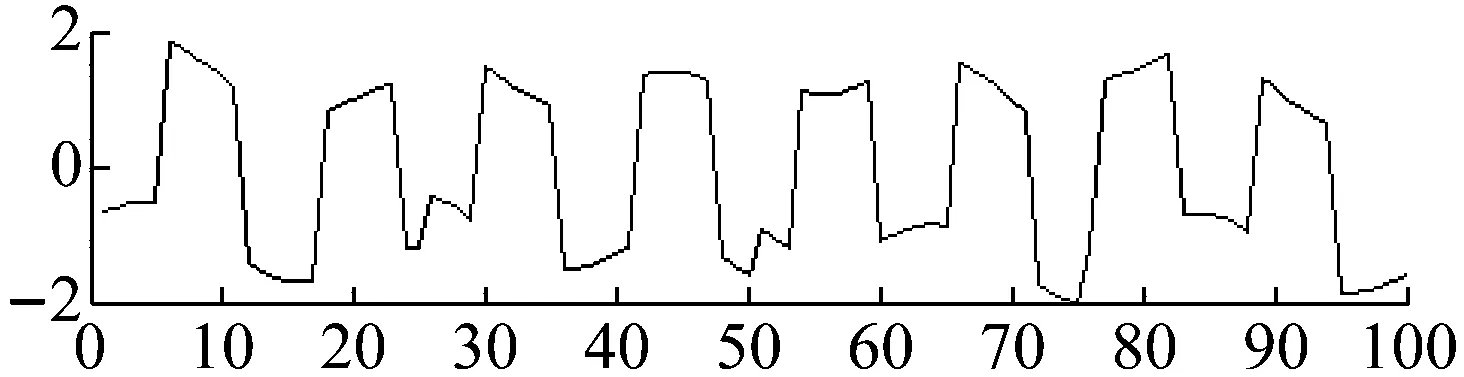

图7 混合信号Fig.7 Mixed signals
对于通常问题,30个粒子已足够,对于较复杂的问题,粒子数可取为50,当种群粒子数小于50时,可发现种群大小对PSO性能有显著的影响,当种群粒子数大于50时,对PSO性能影响较小[17]。因此在对比实验分析中,粒子个数分别选为10、20、30、40、50、60、70;基本膜个数选择为从2到8的整数。如图8、9所示,分别为不同粒子数和基本膜个数的分离效果曲线。从图8、9可以看出当粒子数为30,基本膜个数为5时,相似系数的值最大,表明MCPSO算法的分离效果最好。
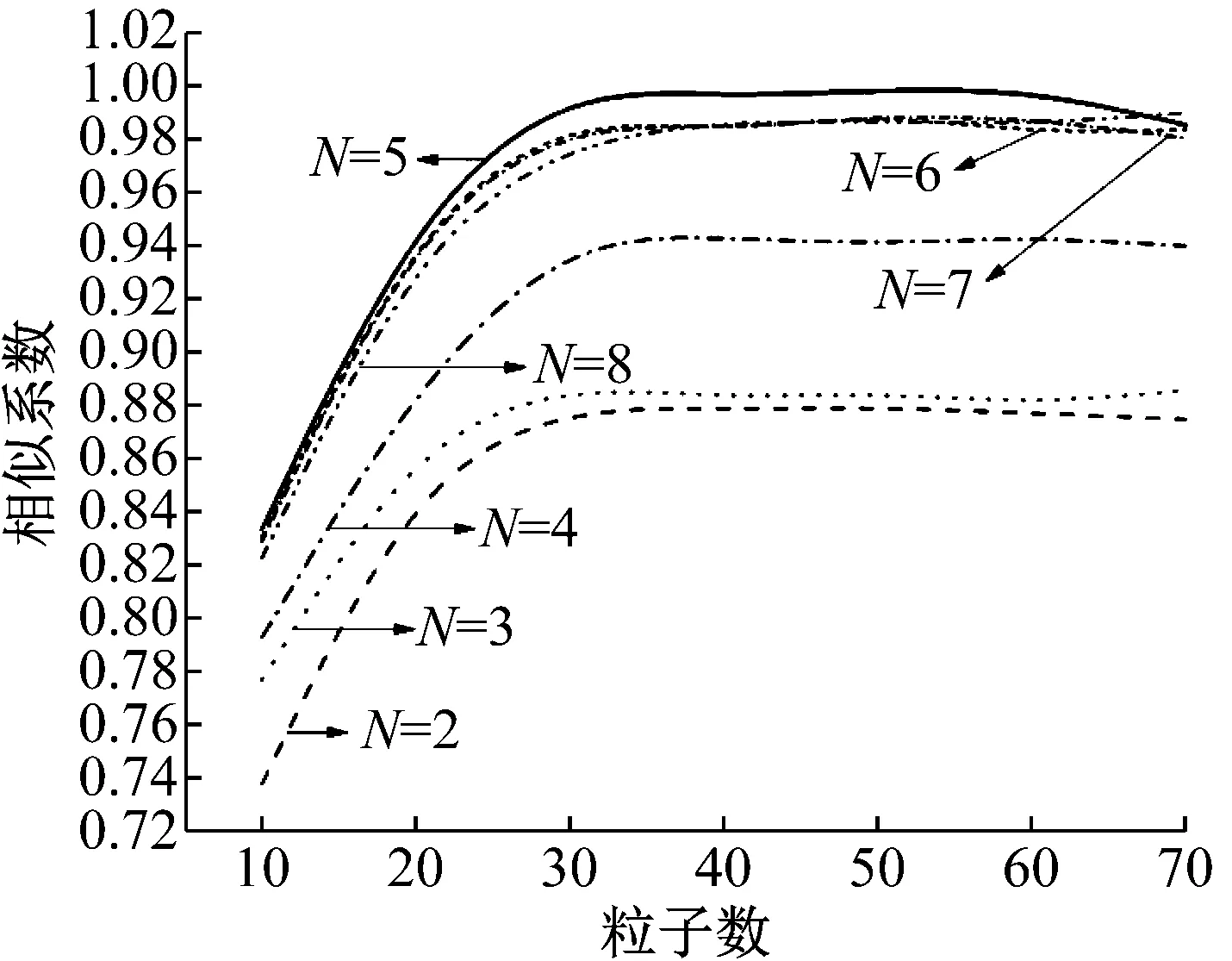
图8 基本膜个数对分离效果的影响Fig.8 The influence of membrane number to separation effect
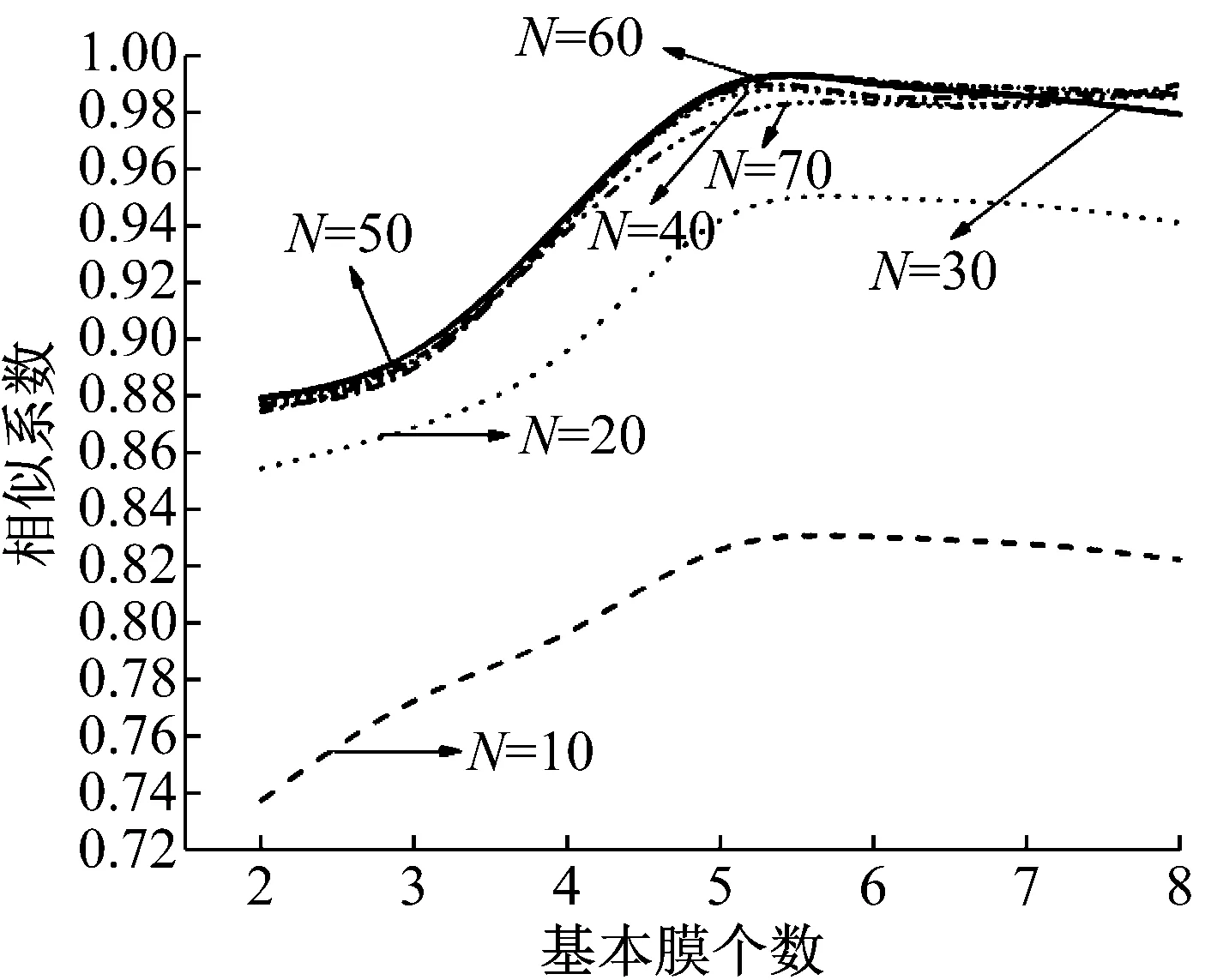
图9 粒子数对分离效果的影响Fig.9 The influence of particle number to separation effect

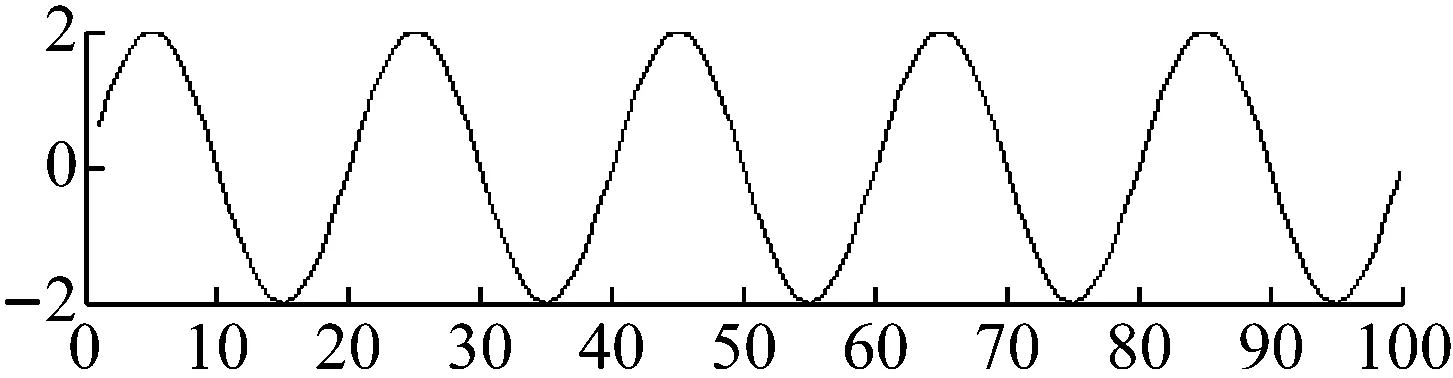

图10 MCPSO分离信号Fig.10 Separated signals of MCPSO
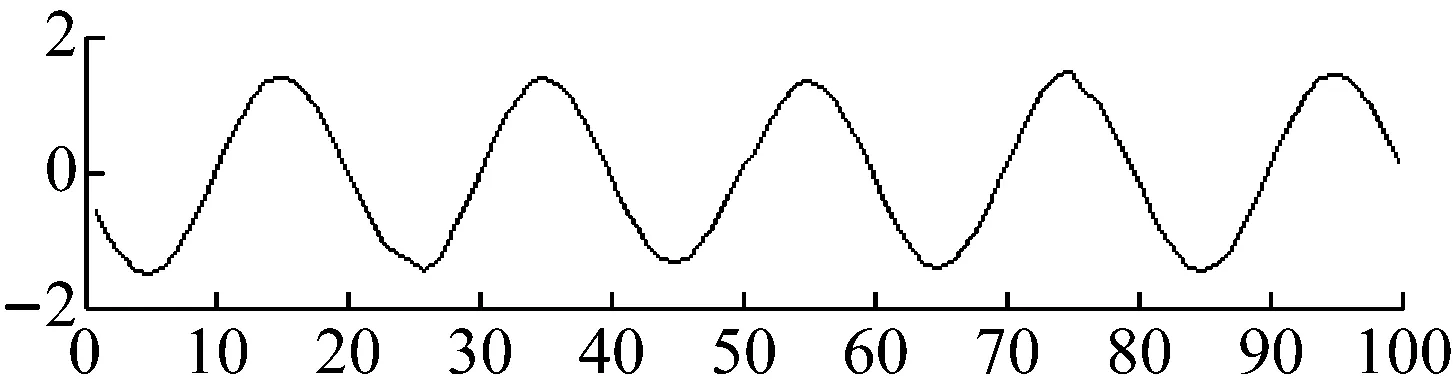


图11 线性PSO分离信号Fig.11 Separated signals of linear PSO
从图10、11、12分离结果图可以看出,线性PSO算法分离后的正弦信号、方波信号、锯齿波信号均有变形情况,分离效果不够理想;非线性PSO算法分离后的方波信号有变形情况,但正弦信号和锯齿波信号分离效果较好;提出的MCPSO算法分离出的3组信号均与源信号有较好的吻合,分离效果较为理想,提高了分离精度。



图12 非线性PSO分离信号Fig.12 Separated signals of nonlinear PSO
算法的分离效果的好坏可以选用性能指数PI(Performance Index)来衡量,其定义如下

(12)
式中:g(i,j)为矩阵G的第(i,j)个元素,而G为全局矩阵,即分离矩阵与混合矩阵的乘积,PI值越小表明分离的效果越好。图13为MCPSO算法和线性PSO算法以及非线性PSO算法性能指数PI的收敛曲线比较结果。从图13可以看出,MCPSO算法在迭代28步时即可收敛,这是由于膜计算并行处理的优点,提高了算法的收敛速度,降低了计算复杂度;线性PSO算法在迭代68步后才开始收敛;非线性PSO算法在迭代62步开始收敛,虽然非线性PSO算法基本可以将源信号分离出来,但是在收敛速度上与MCPSO算法相比较低。因此,MCPSO算法在收敛速度上要优于线性PSO算法和非线性PSO算法。
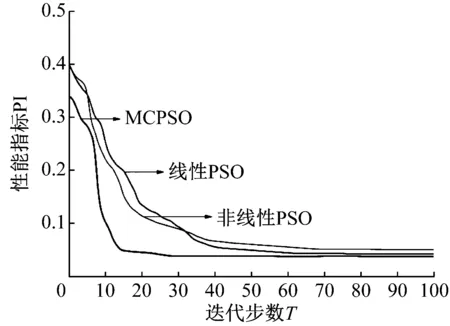
图13 PI收敛曲线Fig.13 Convergence curves of performance index
为了定量的说明信号的盲源分离效果,需要多种评价指标来衡量,来从不同角度反映分离信号与源信号之间的误差度量[18]。本文采用相似系数ρij、二次残差VQM以及性能指数PI三种评价指标。
二次残差采用带幅值修正因子的计算公式[19],表达式如下
(13)
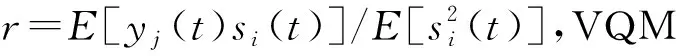
表1为MCPSO算法、线性PSO算法以及非线性PSO算法的盲源分离评价指标的比较。从表1可知,MCPSO算法与线性PSO算法和非线性PSO算法相比,相似系数更接近于1,二次残差VQM更小,PI性能指数更小。表明MCPSO算法的盲源分离效果最好。
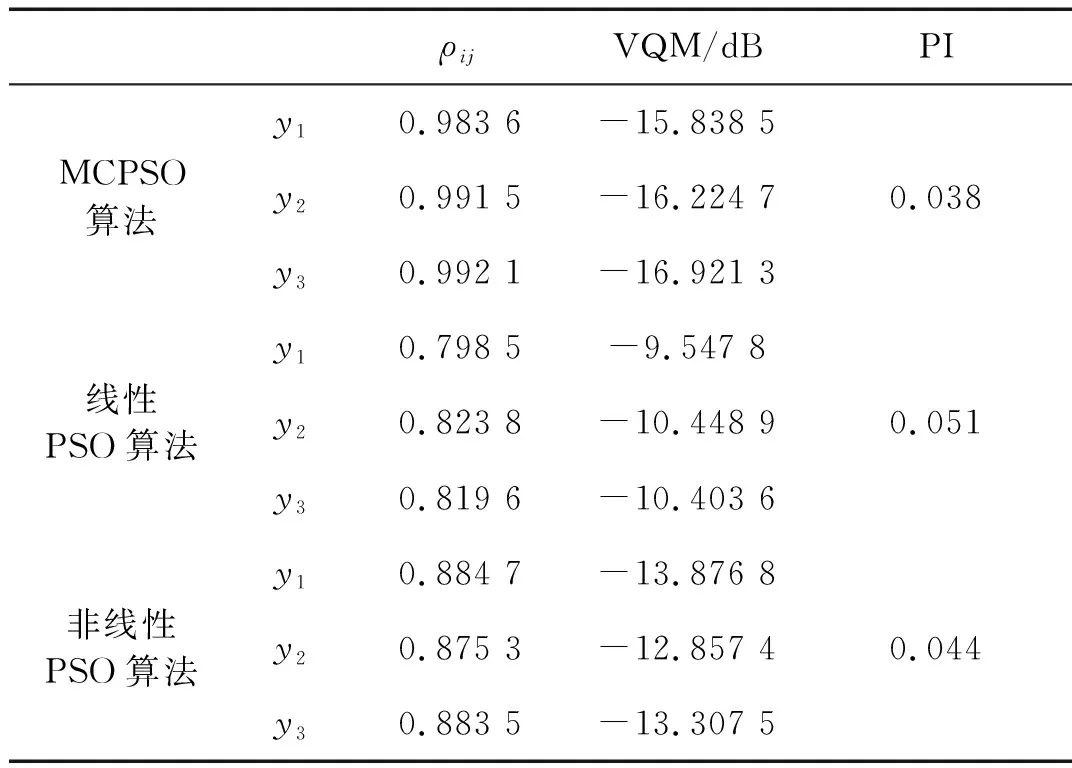
表1 盲源分离评价指标对比Tab.1 Evaluation indexes comparison of blind source separation
4.2 应用实例
本节利用所提出的算法处理人员脚步和车辆实测振动信号。采集装置使用Geopen地震仪,如图14所示。采样频率设置为1 kHz,采样点数为16×103,采样率设置为1 ms。实验主要分为三组:第一组实验设计为单独采集单人行走脚步振动信号;第二组实验设计为单独采集车辆(汉兰达2.0T)振动信号;第三组实验设计为同时采集第一组试验中的人员和第二组实验中的车辆振动混合信号。前两组实验的设计是为了与分离出的信号作对比,证明MCPSO算法的有效性和准确性。如图15所示,分别为人员脚步振动信号和车辆振动信号的时域波形。图16所示为传感器的观测信号,即采集到的单人行走脚步振动和车辆振动的混合信号。图17为MCPSO算法对观测信号进行分离后的信号。图18为人员脚步振动源信号与分离后信号的频谱对比。图19为车辆振动源信号与分离后信号的频谱对比。

图14 采集实验Fig.14 The experiment of vibration signal collection

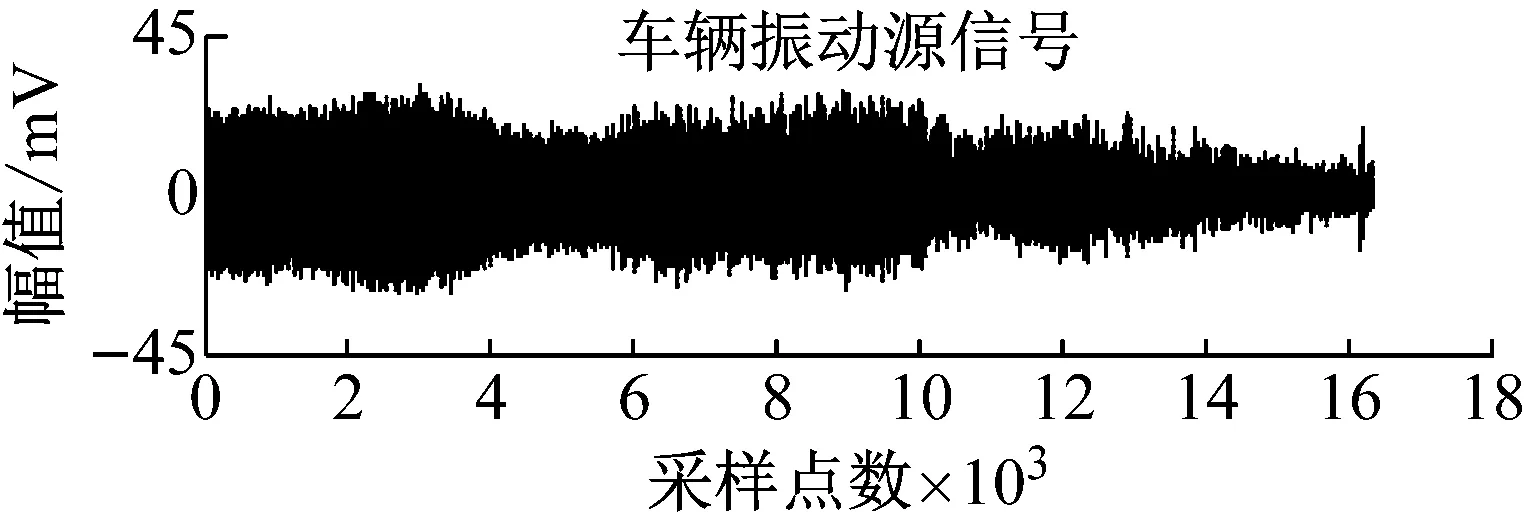
图15 人员脚步和车辆振动信号时域波形Fig.15 The time domain waveform of step and vehicle vibration signals
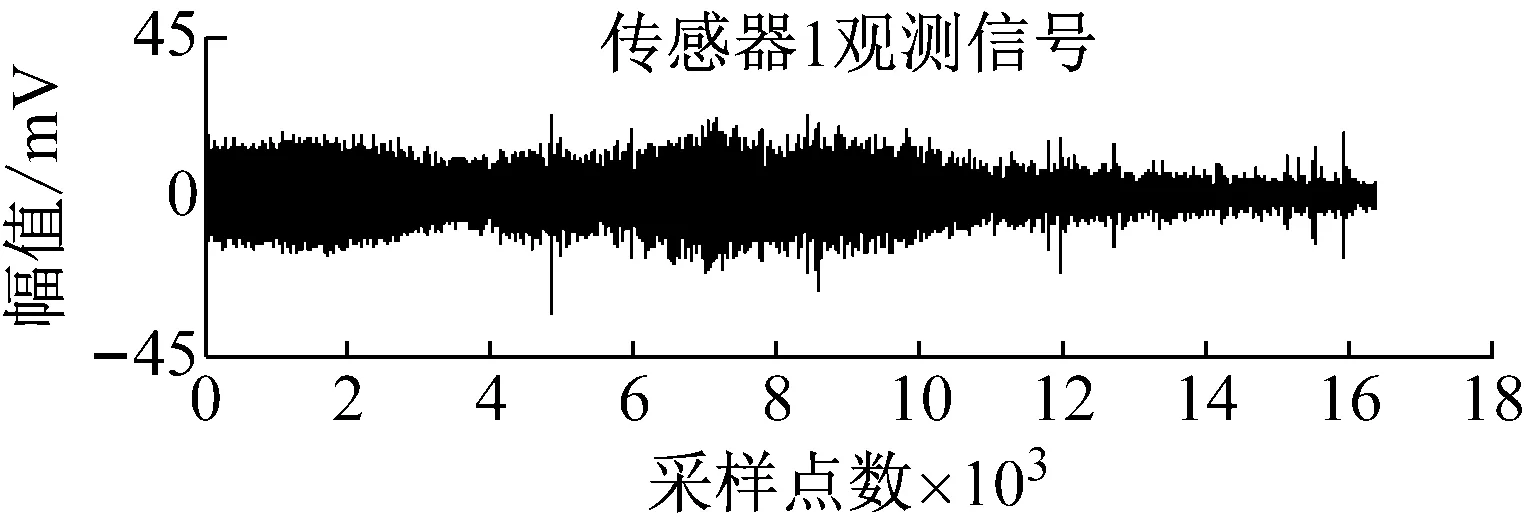

图16 传感器观测信号Fig.16 The sensor signals
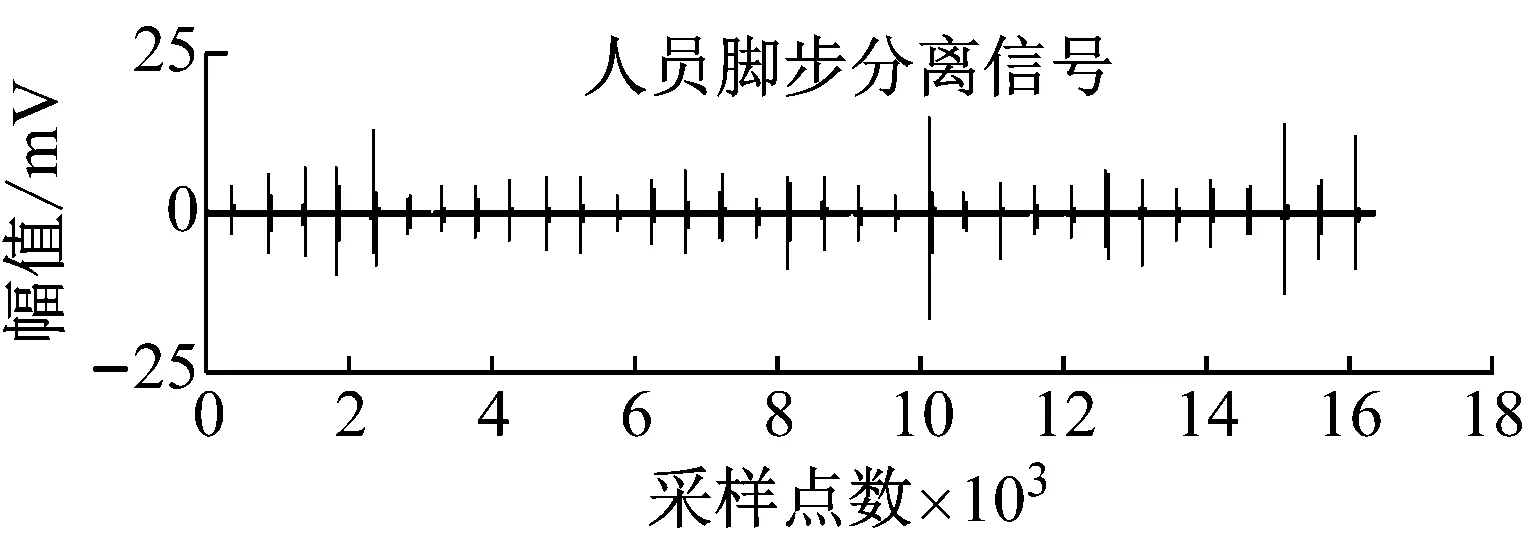
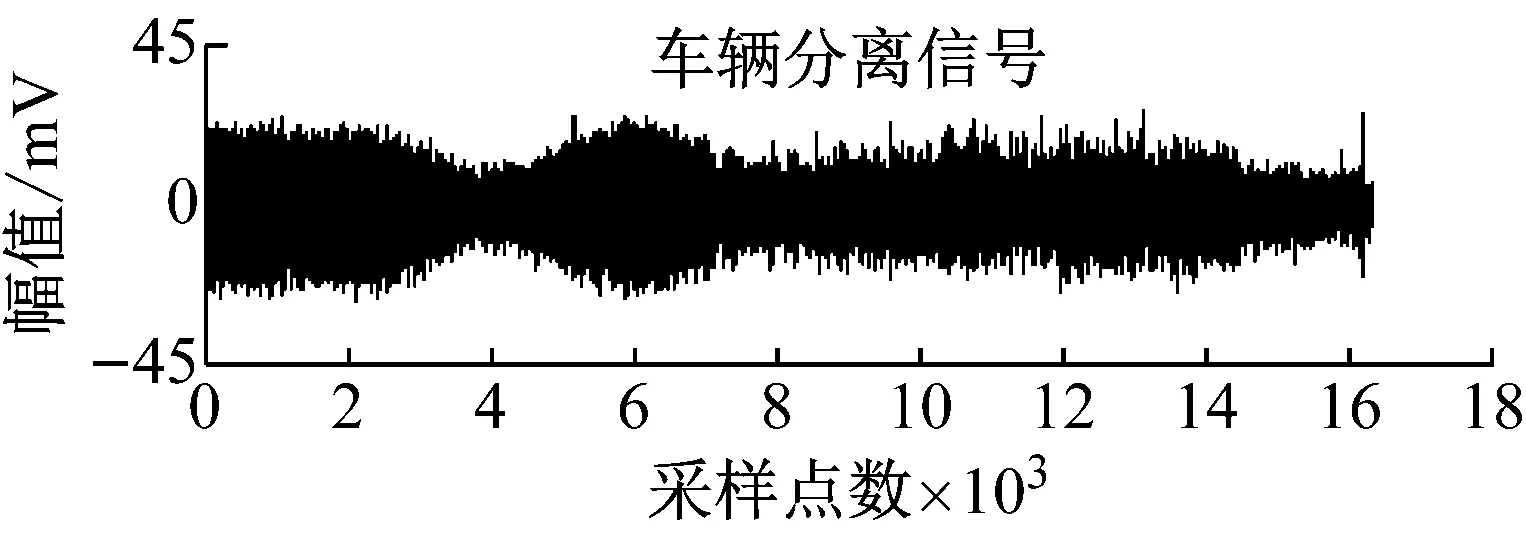
图17 分离信号Fig.17 The separated signals


图18 人员脚步振动源信号与分离信号的频谱对比Fig.18 Spectrum comparison between the step source signals and the separated signals
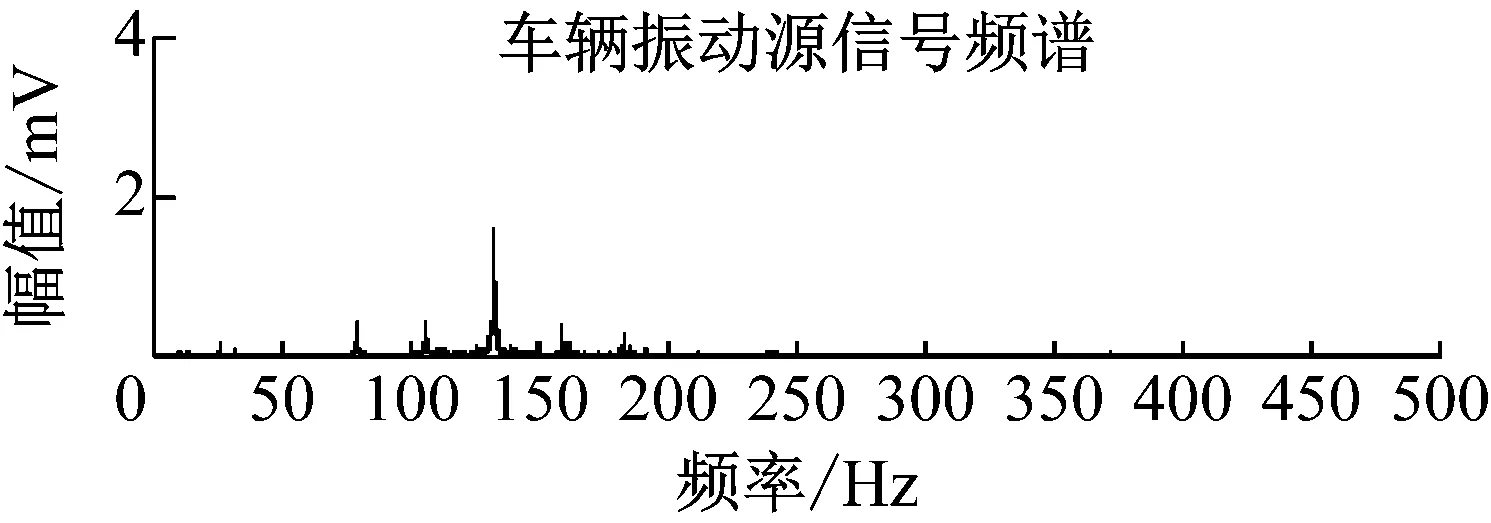
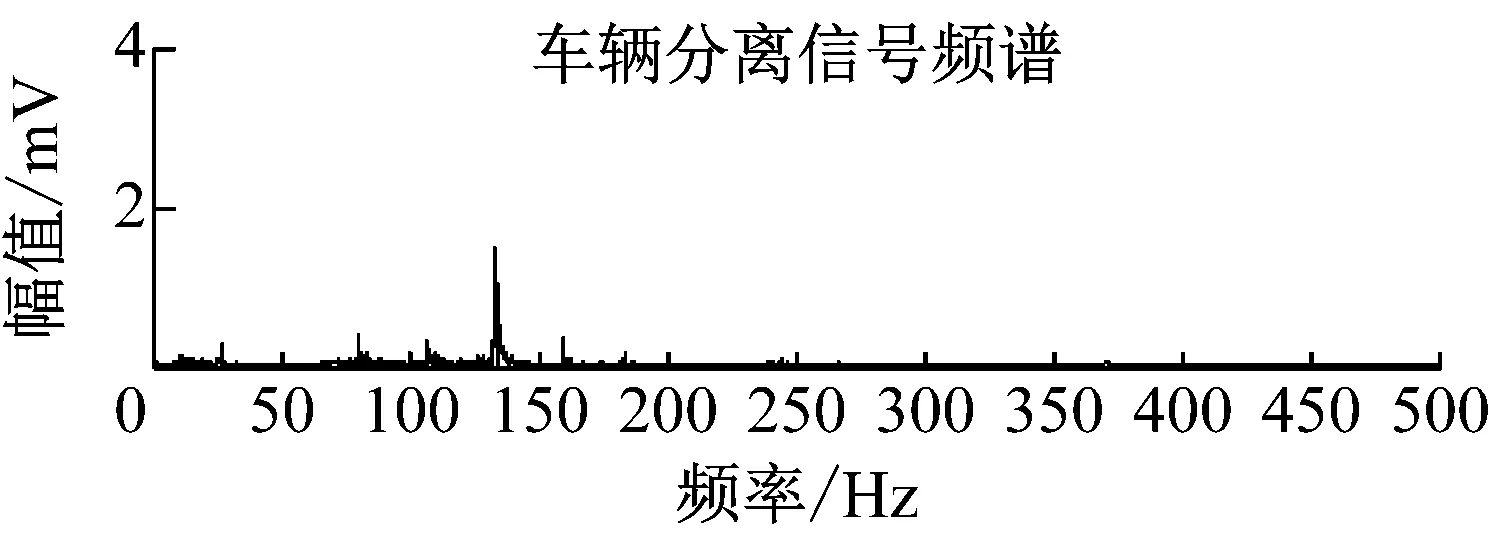
图19 车辆振动源信号与分离信号的频谱对比Fig.19 Spectrum comparison between the vehicle source signals and the separated signals
为使结果更可靠,对观测信号多次分离,计算时频域评价指标,取多次分离实验的平均值作为最终的评价指标。如表2所示,三种时域评价指标均能反应出MCPSO算法的分离效果较好。对人员脚步振动源信号和分离信号以及车辆振动源信号和分离信号做频谱分析,两种分离信号的频率与两种源信号的频率基本相同,脚步振动源信号和分离信号频率主要在50 Hz以下,车辆振动源信号和分离信号频率主要在200 Hz以下。

表2 MCPSO的盲源分离时频域评价指标Tab.2 The time-frequency domain evaluation indexes of MCPSO blind source separation
5 结 论
本文将膜计算引入到粒子群优化算法中来进行信号的盲源分离,将粒子放入基本膜中,通过计算适应度,将各基本膜中粒子最优位置通过膜规则输送到表层膜中,再将表层膜中粒子最优值作为群体最优值返回给各基本膜来对粒子的位置和速度进行更新,在保证粒子局部搜索精度的同时,也满足了粒子全局搜索的多样性。膜计算的引入简化了惯性权重的取值问题,只需要考虑局部搜索时惯性权重的取值,降低了计算复杂度,提高了算法的收敛速度,有效地解决了PSO全局搜索和局部搜索之间的矛盾。MCPSO算法可以提高信号的分离精度,且具有较快的收敛速度,有效的避免了标准PSO算法粒子容易陷入早熟的问题。通过仿真实验对比和实例应用验证了MCPSO算法的有效性。

