织物复合材料空间可展桁架模态试验与分析

张祎贝， 高冀峰， 陈务军， 张大旭， 房光强， 曹争利， 彭福军

(1. 上海交通大学 空间结构研究中心, 上海 200240； 2. 上海宇航系统工程研究所, 上海 201109)

随着航天科技的迅速发展以及对航天任务需求不断提高，航天器结构正日益朝着大型化、轻量化和模块化的方向发展。空间可展桁架结构以其质量轻、收纳比高、结构形式可简单重复等优点，在航天工程中得到了广泛的应用。现阶段的空间可展结构已达到101～102m量级，并朝着公里级的方向发展。这种大尺寸的结构在温度梯度载荷、空间碎片撞击或航天器姿态调整等载荷作用下，极易产生长时间大幅度的振动，严重影响航天器的正常工作。因此，在结构的设计阶段，就要对它的自振频率和振型提出要求，地面试验阶段需要进行振动试验和模态识别分析[1-3]。

织物复合材料具有质地轻、强度高、抗损伤性高、韧性好等特点，是制作空间可展桁架结构的理想材料。关于这类材料仿真分析较多，目的是分析材料特性[4]；构件级的实验也很多，目的是建立相应材料的本构方程[5-8]。由于这种材料制成的结构尺寸大、刚度低，需要结合重力卸载装置来模拟微重力环境。这种试验难度大、成本高，因此相应的结构级的试验较少。

为提高桁架结构的整体刚度，通常在面内布置加劲索，并在索内施加一定的预应力。一般认为在一定范围内，索内预应力大小的变化对结构的自振频率影响很小。这种认识不够全面，通过对比试验和仿真分析结果，讨论预应力对加劲索和结构的影响。

开展了大型织物复合材料空间可展桁架的微重力模态试验和仿真分析，试验对象为一个单节桁架结构(长约2.7 m)和一个五节桁架结构(长约14 m)。首先在气动-电磁悬挂系统上进行模态试验，得到桁架结构的自振频率和振型数据；随后对结构进行简化，将简化模型导入到有限元软件进行仿真分析，并将仿真结果与试验进行对比分析。

1 结构及材料参数

研究的桁架结构如图1所示，由三角形隔板、空心圆管、加劲索及吊绳组成(吊绳属于重力卸载装置的一部分，实际结构无吊绳)。隔板横截面为空心矩形，采用铺层复合材料制作，详细参数见表1。圆管为空心圆管，采用编织复合材料制作，详细参数见表2。加劲索及吊绳采用凯夫拉材料制作，详细参数见表3。

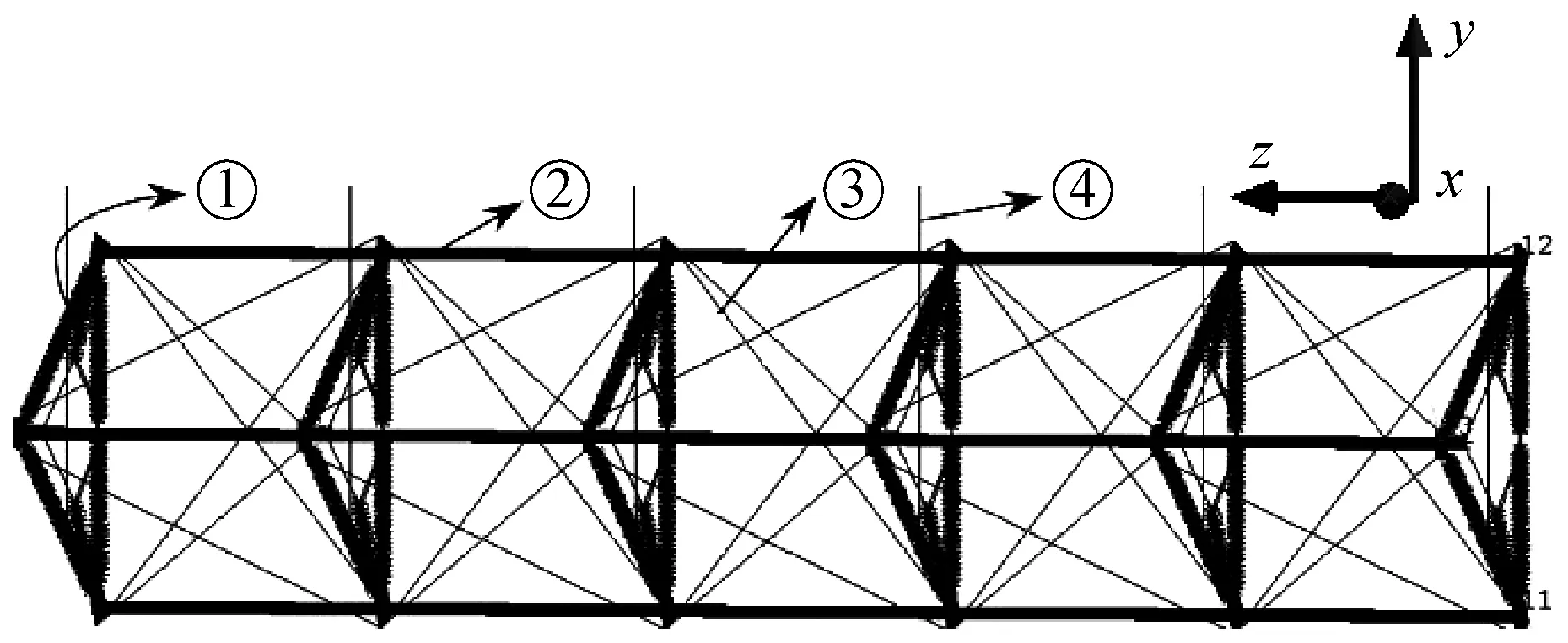
①-隔板； ②-圆管； ③-斜加劲索； ④-吊绳图1 空间可展桁架结构图Fig.1 Sketch of the space deployable truss表1 三角形隔板材料及结构参数Tab.1 Material and structural parameters of the triangular spacer

密度/(kg·m-3)弹性模量/GPa泊松比截面宽/mm截面高/mm截面竖向壁厚/mm截面横向壁厚/mm2 780600.3105023

表2 空心圆管材料及结构参数Tab.2 Material and structural parameters of the circular hollow section pipe

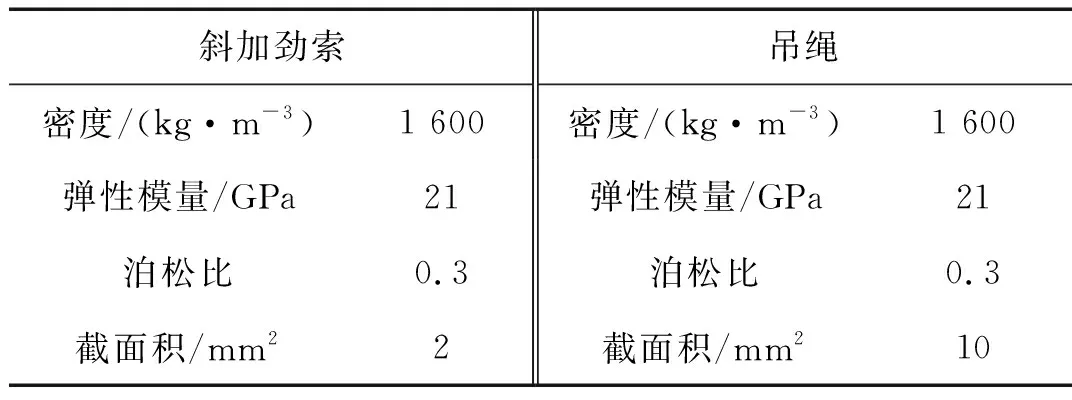
表3 斜加劲索与吊绳材料及结构参数Tab.3 Material and structural parameters of the stiffend cable and the lifting rope

2 地面微重力模态试验

采用气动-电磁悬挂系统作为重力卸载装置来模拟微重力环境。桁架结构整体由凯夫拉绳悬吊，悬吊点为各个三角形隔板顶边上的一点，吊绳通过重心，使桁架搁置阵面的侧面垂直于地面；吊绳顶端与气动-电磁悬挂装置连接；气动-电磁悬挂装置在竖直方向上可提供恒定的平衡试件重力的悬挂力，并能在竖直方向无摩擦随动[9]。通过上述装置来模拟微重力环境。

在结构端部三角形隔板的底角施加简谐激励，频率从1～10 Hz逐步施加，采用西门子LMS模态测试系统识别结构的自振频率及振型。

分别进行了单节、五节桁架的地面微重力模态试验。单节桁架试验中去掉斜加劲索，主要研究隔板与圆管的变形特性；五节桁架试验包含预应力斜加劲索，主要研究结构的整体变形特性。

2.1 单节无斜加劲索模态试验

结构由两侧三角形隔板、中间空心圆管及吊绳组成，结构形式如图2。在每个隔板的3个角点及各根圆管的中部布置传感器。模态试验结果见表4。

单节桁架结构的1阶模态为扭转变形模态，2、3阶为隔板面外弯曲变形模态。即结构在振动过程中以扭转及隔板面外弯曲变形为主。

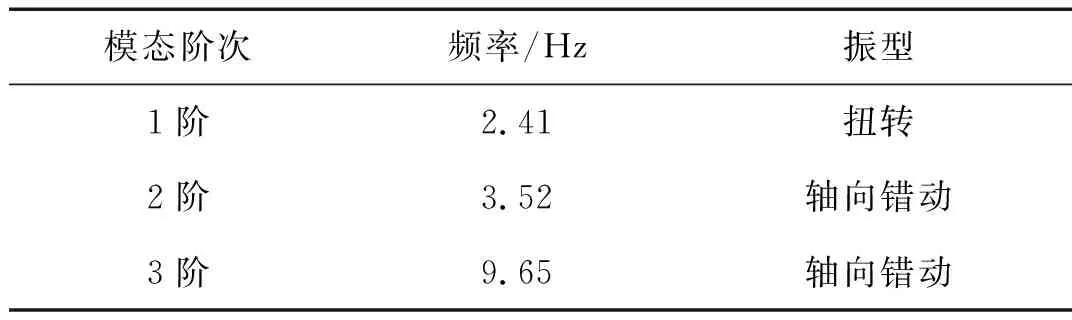
表4 单节无斜加劲索桁架模态试验结果Tab.4 Modal experiment result of the one layer truss without stiffened cable

2.2 五节含斜加劲索模态试验

结构由三角形隔板、空心圆管、斜加劲索及吊绳组成，结构形式如图1。由于要布置的传感器数量较多，因此仅在每个隔板的3个角点布置传感器。模态试验结果如表5。

五节桁架结构的1阶模态为扭转变形模态，2、4阶为整体弯曲变形模态，3阶为弯扭组合变形模态。即结构在振动过程中以扭转及整体弯曲变形为主。

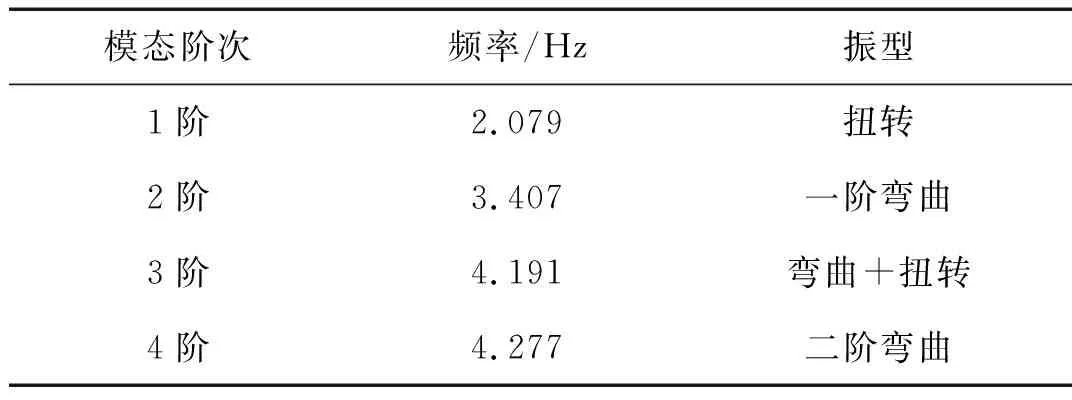
表5 五节含斜加劲索模态试验Tab.5 Modal experiment result of the five layers truss without stiffened cable

3 有限元仿真分析

3.1 有限元建模

空心圆管由织物复合材料制作，自身结构形式复杂，若考虑复杂的本构模型，计算量过大。因此将圆管简化为正交各向异性材料结构，并建立圆柱坐标系定义参数方向，采用Shell单元建模。

三角形隔板结构形式如图3，每个隔板由两片子隔板通过中间点连接而成，连接点为图中黑点位置，这样的结构形式可简化隔板的制作工艺。子隔板又分为实心和空心部分：子隔板三个角点附近的部分为实心结构，如图4所示红圈内的部分，采用Solid单元建模；其余部分为空心结构，采用Beam单元建模；两种单元连接的位置采用MPC(Multi Point Constraint )方法设置接触对，保证连接；实现两个子板固结的连接件采用Beam单元建模，材料参数设置为较刚的材料(弹性模量200 GPa)。隔板采用铺层复合材料加工制作，为方便计算，将隔板简化为各向同性材料结构。

吊绳和斜加劲索均采用Link单元建模，且设置为只能受拉。吊绳与斜加劲索的单元刚度阵由两部分组成，分别为单元弹性刚度阵Kelastic和单元荷载刚度阵Kload(与预应力有关)，即

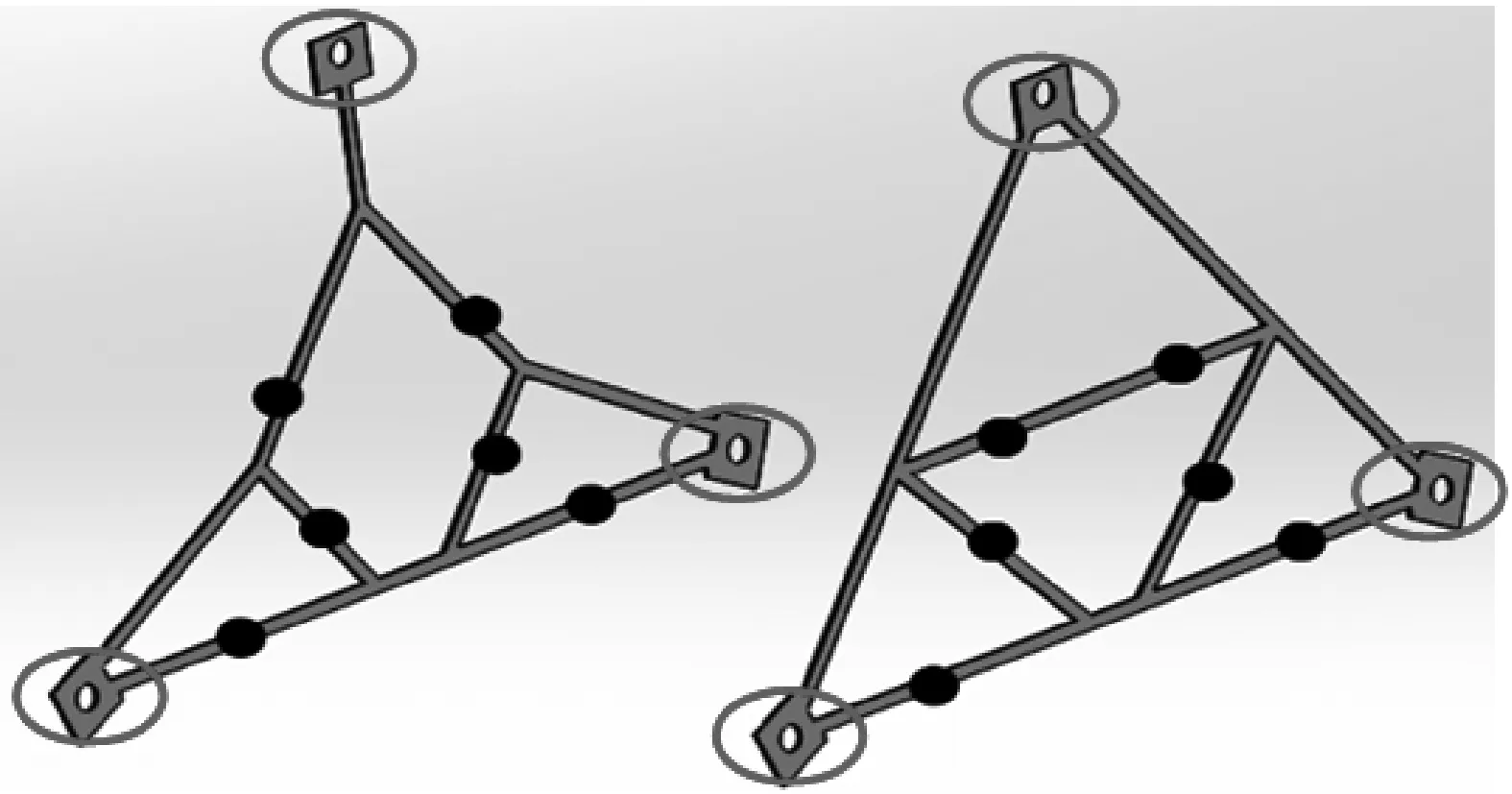
图3 三角形隔板详细结构Fig.3 Detail sketch of the triangular spacer

K=Kelastic+Kload

(1)

3.2 单节无斜加劲索仿真结果

结构总重约53 kg，故每根吊绳施加26 MPa的预应力。对建立的单节桁架模型进行模态仿真计算，提取前5阶模态如图4。为方便观察，略去结构中的吊绳。单节无斜加劲索试验与仿真对比结果如表6。

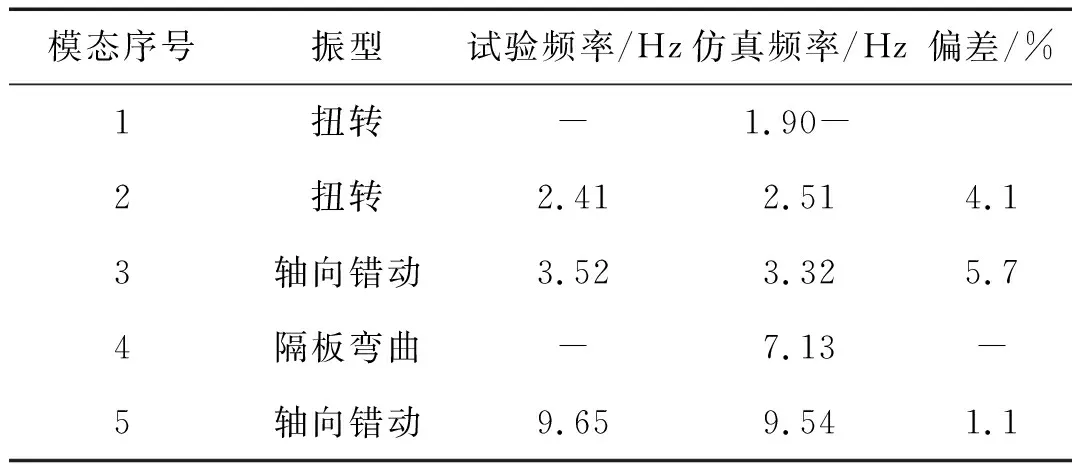
表6 单节无斜加劲索试验与仿真结果对比Tab.6 Result comparison between the experiment and simulation of the single part structure

仿真的前2阶模态均为扭转变形模态，而试验前3阶模态仅有1个扭转变形模态，再根据其余阶模态的对应关系，假定试验中未测出1.90 Hz附近的扭转变形模态，则试验1阶频率(2.41 Hz)与仿真2阶频率(2.51 Hz)对应；试验2阶频率(3.52 Hz)与仿真3阶频率(2.32 Hz)对应；试验3阶频率(9.65 Hz)与仿真5阶频率(9.54 Hz)对应；仿真4阶模态(7.13 Hz)主要表现为隔板的弯曲变形，由于在隔板上未布置传感器，故此阶模态在试验中未测出。调整后仿真与试验对比结果如表6。前3阶振型基本对应，频率最大偏差5.7%，可以认为仿真结果与试验结果对应良好。

3.3 五节含斜加劲索仿真结果

结构总重约160 kg，故每根吊绳施加26 MPa的预应力。试验中没有测定每根斜加劲索的预应力，故仿真中，大致将每根斜加劲索的预应力取为5 MPa，相当于10 N的预紧力。

对建立的五节桁架模型进行模态仿真计算，提取前5阶模态如图5，为方便观察，略去结构中的斜加劲索及吊绳。五节含斜加劲索试验与仿真对比结果如表7。

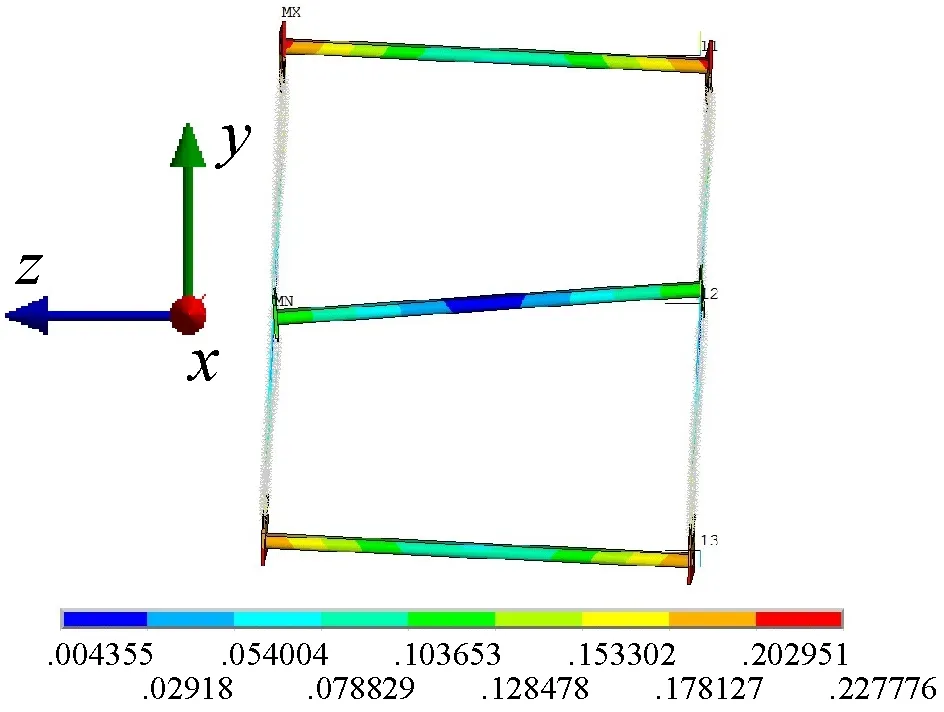
(a) 1阶模态

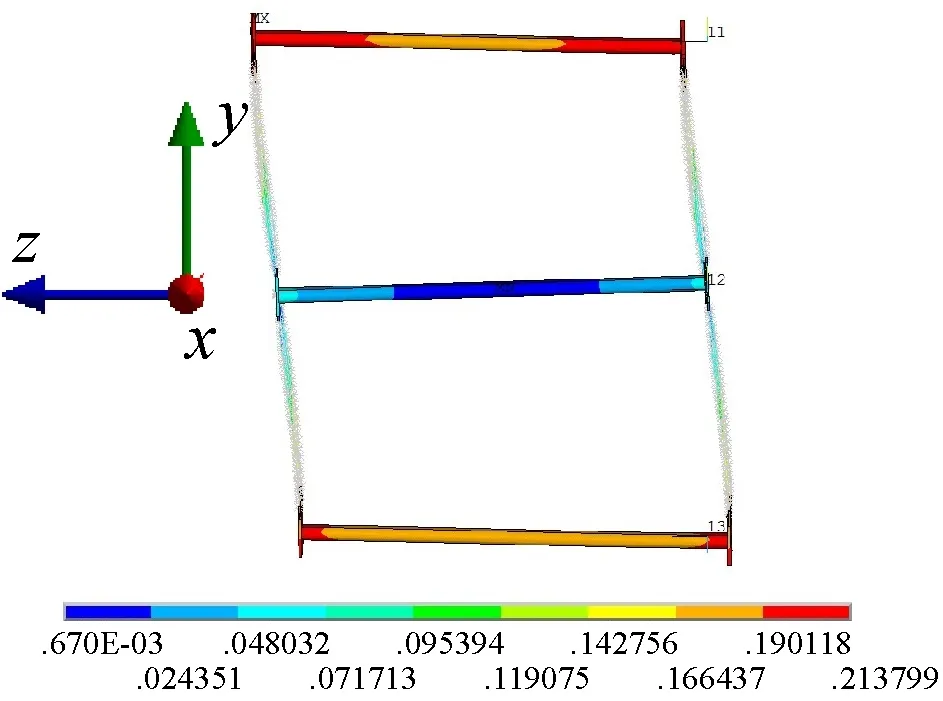
(b) 2阶模态

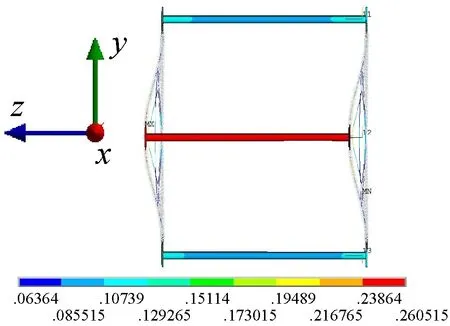
(c) 3阶模态

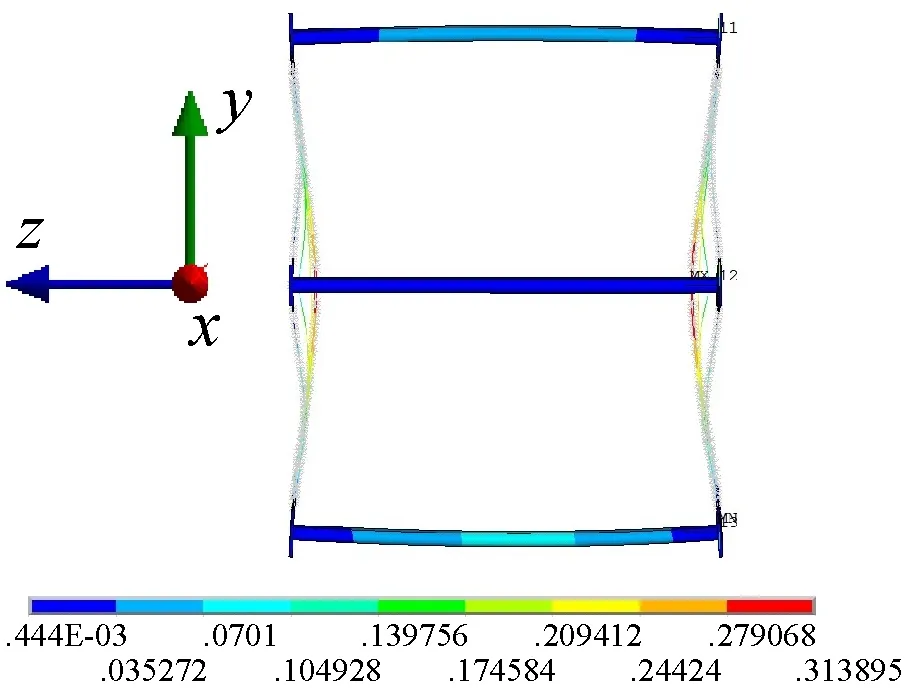
(d) 4阶模态

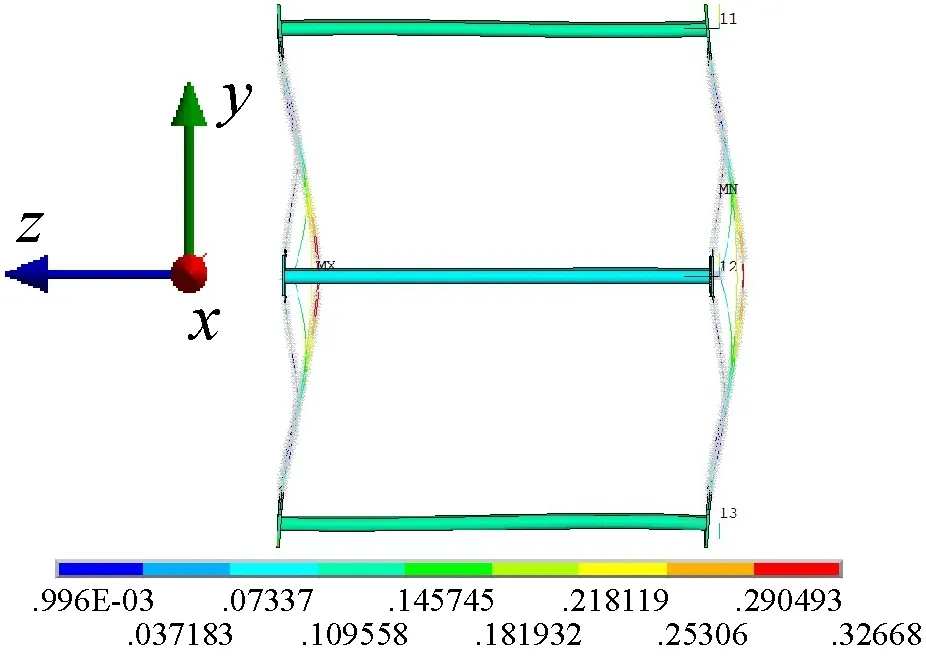
(e) 5阶模态图4 单节无斜加劲索仿真模态Fig.4 Simulation modal of the single part structure

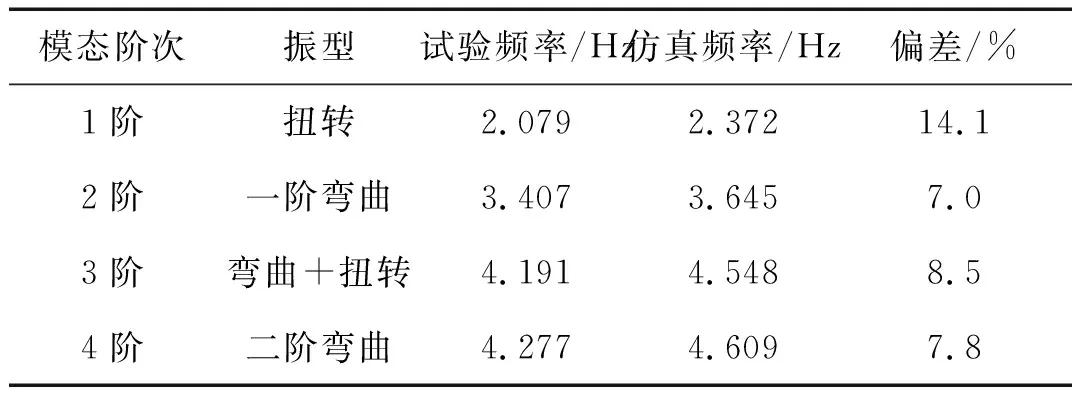
表7 五节含斜加劲索试验与仿真结果对比(一)Tab.7 Result comparison between the experiment and simulation of the five parts structure (1)

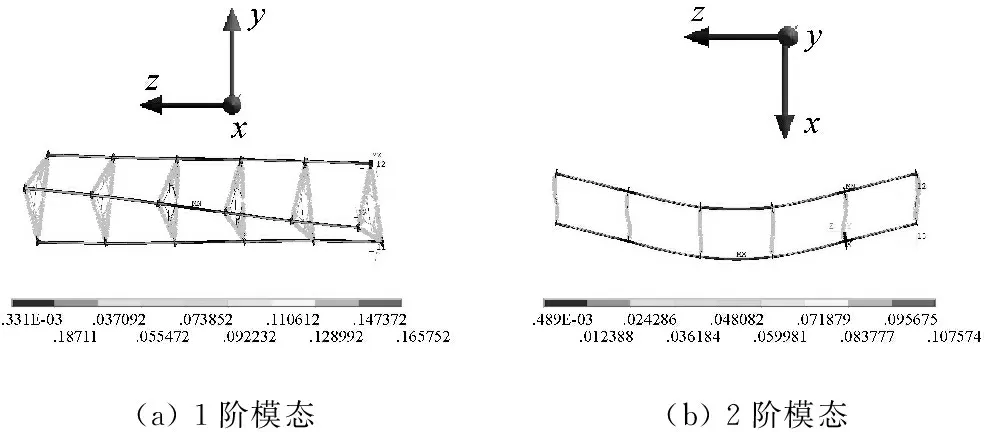
(a) 1阶模态(b) 2阶模态

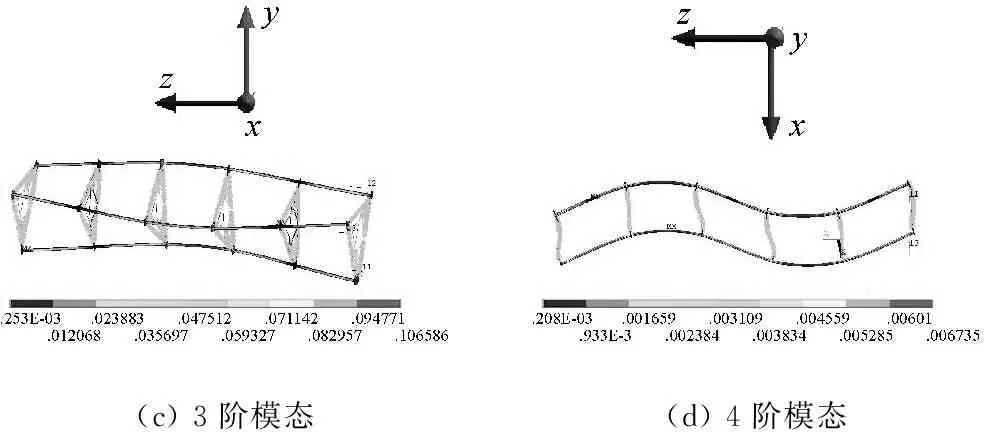
(c) 3阶模态(d) 4阶模态

图5 五节含斜加劲索模态仿真结果

Fig.5 Modal simulation results of the five parts structure

由图5可知，仿真结果的振型与试验结果对应关系较好，1阶振型均为扭转变形，2阶振型均为一阶弯曲变形，3阶振型均为弯扭组合变形，4阶振型均为二阶弯曲变形。上述弯曲变形均为水平面内弯曲。

从表7中看出，仿真频率与实验频率相比普遍偏大。分析其中的原因发现，结构自振频率与斜加劲索的弹性模量有很大关系。由于斜加劲索股与股之间存在间隙，在拉伸的初始阶段斜加劲索未被完全拉紧，其应力应变关系是非线性的，斜加劲索的有效弹性模量Eeq可用Ernst公式表示

(2)

式中：E为斜加劲索的固有弹性模量；γ为斜加劲索容重；L为斜加劲索长度；α为斜加劲索水平倾角；σ为斜加劲索预应力[11-12]。

在拉伸的初始阶段，斜加劲索的有效弹性模量Eeq低于其固有弹性模量E，当应力达到一定值之后，式分母项趋于1，斜加劲索的有效弹性模量Eeq才与其固有弹性模量E相当。模态试验中，实际斜加劲索的预应力较小，处在拉伸过程的非线性阶段，此阶段的有效弹性模量小于固有弹性模量。仿真中，斜加劲索的弹性模量设置为21 GPa，对应于固有弹性模量，高于实际值，导致仿真频率高于试验结果。故需要详细考虑斜加劲索弹性模量的问题。

3.4 斜加劲索的拉伸实验

采用UTM4503电子万能试验机对斜加劲索作拉伸试验，测量斜加劲索的弹性模量。试件测试长度为30 cm，两端采用夹具固定，选用量程为1 kN的传感器。试验结果如图6。

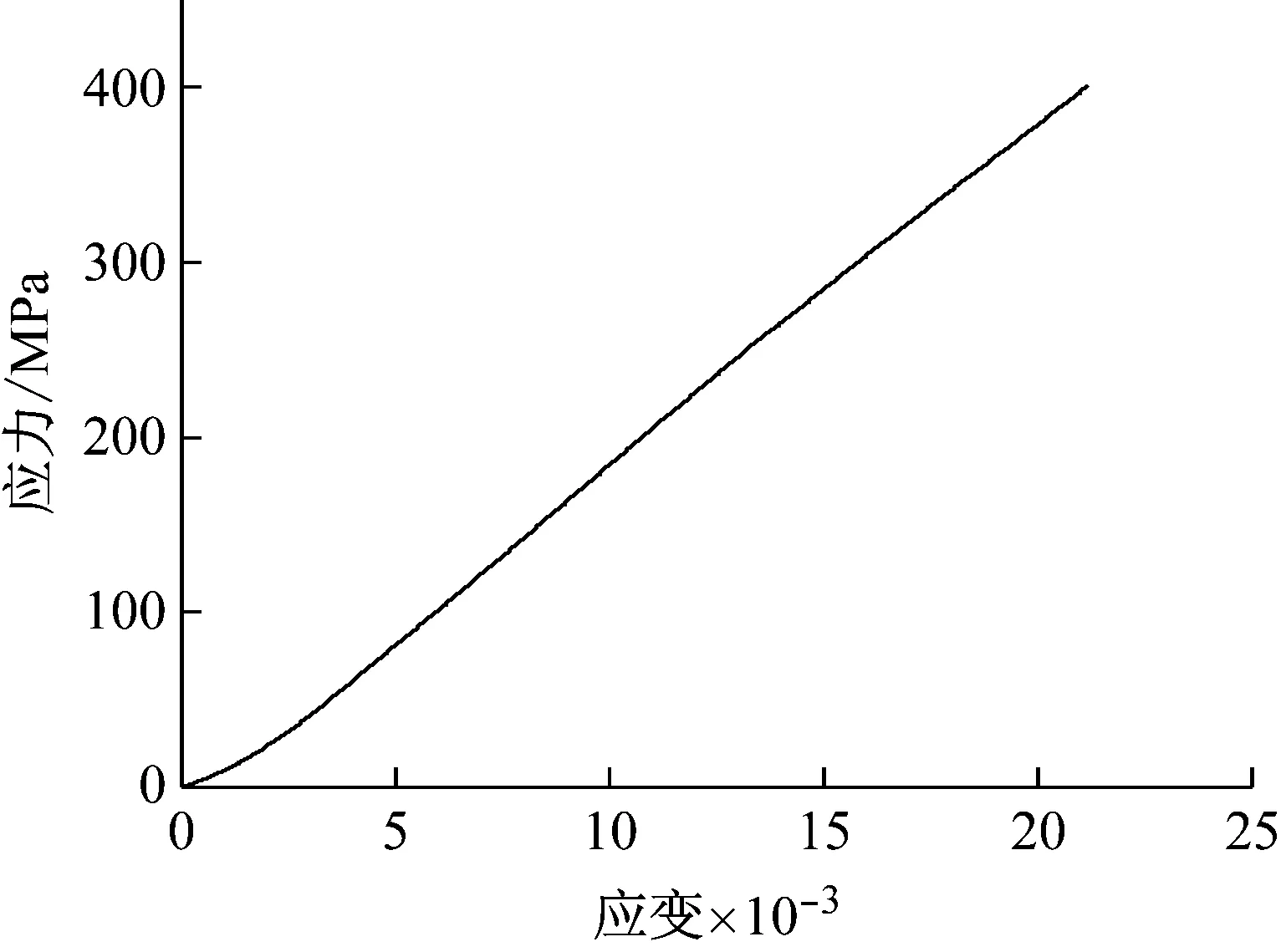
图6 斜加劲索的拉伸试验曲线Fig.6 Stress-strain curve of the stiffened cable

由图6可知，拉伸过程可分为短暂的非线性阶段和随后的线性阶段。线性阶段的固有弹性模量基本为前文所取的21 GPa。

现研究非线性阶段。从图6中，大致可认为应力在0～100 MPa内为非线性阶段。对这段曲线逐点求其切线斜率，近似认为是各应力值下对应的弹性模量。切线斜率采用向后差分的方法近似计算

(3)

结果如图7所示。大致可认为，当应力在0～100 MPa范围内，斜加劲索的弹性模量在10～20 GPa范围内变动。由于试验中斜加劲索的预应力是未知的，故不能通过式或图7直接确定斜加劲索在模态试验中应取的弹性模量。需要在仿真中不断修改斜加劲索的弹性模量，以得到与试验相近的结果。计算发现，当斜加劲索弹性模量取为16 GPa时，仿真所得第1阶频率与实验结果有较好的对应关系。

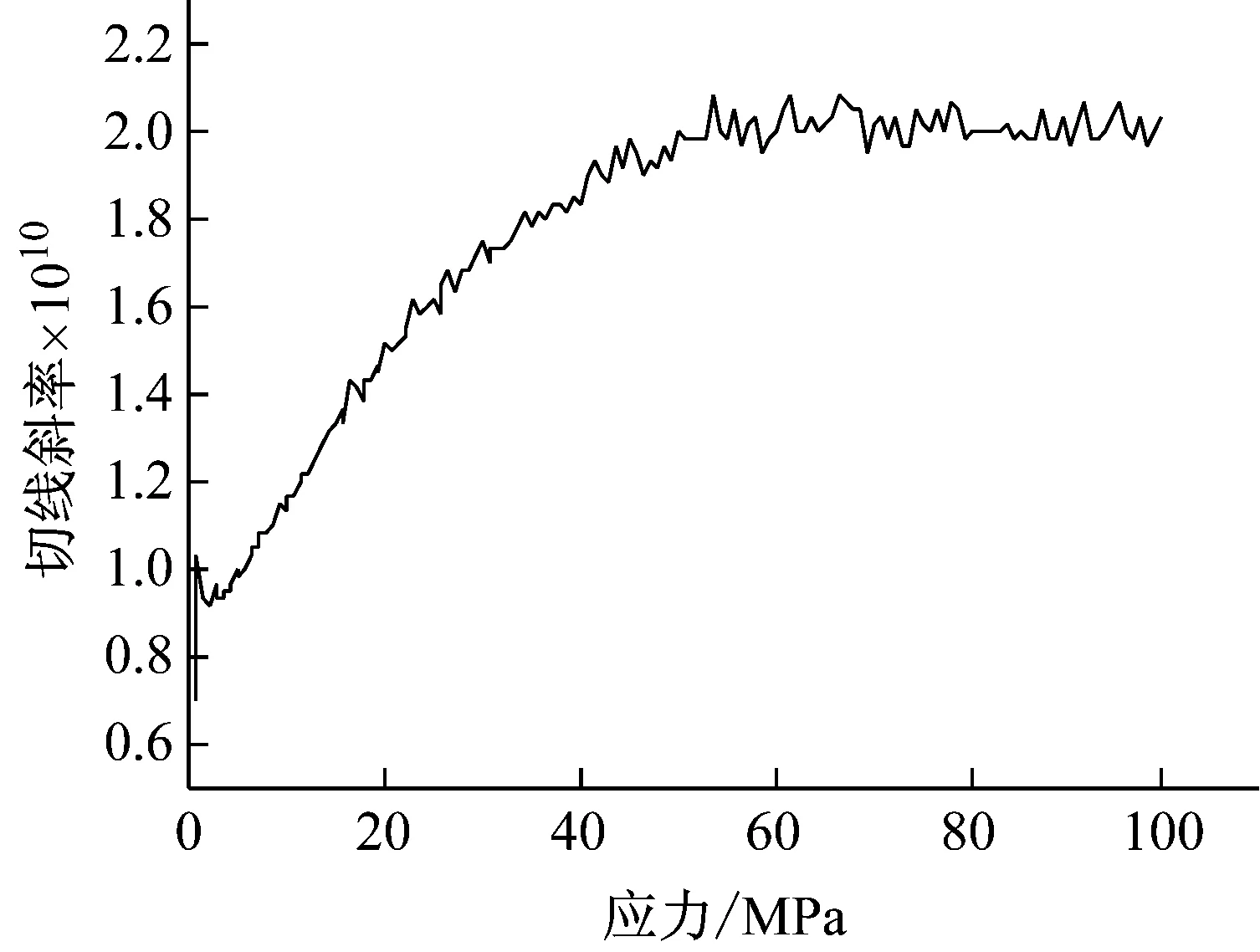
图7 斜加劲索在各预应力下的切线斜率Fig.7 Tangent slope of the stiffened cable

图7对斜加劲索预应力的设定有指导意义，当斜加劲索预应力设为约50 MPa时，其有效弹性模量才能达到固有弹性模量(21 GPa)，对应于100 N的预紧力。

3.5 修改斜加劲索弹性模量后的仿真试验

将斜加劲索的弹性模量设置为16 GPa后，重新进行仿真计算，结果如表8。表8中，仿真分析的1、3阶频率与试验结果基本一致，以结构的扭转变形为主。2、4阶频率与试验结果相差较大，最大为7.6%。此两阶模态主要是结构的弯曲变形，更确切地说是空心圆管的弯曲变形。因此反映了将织物复合材料按正交各向异性材料近似时，计算得到的弯曲模态对应的自振频率与实际值偏差较大。

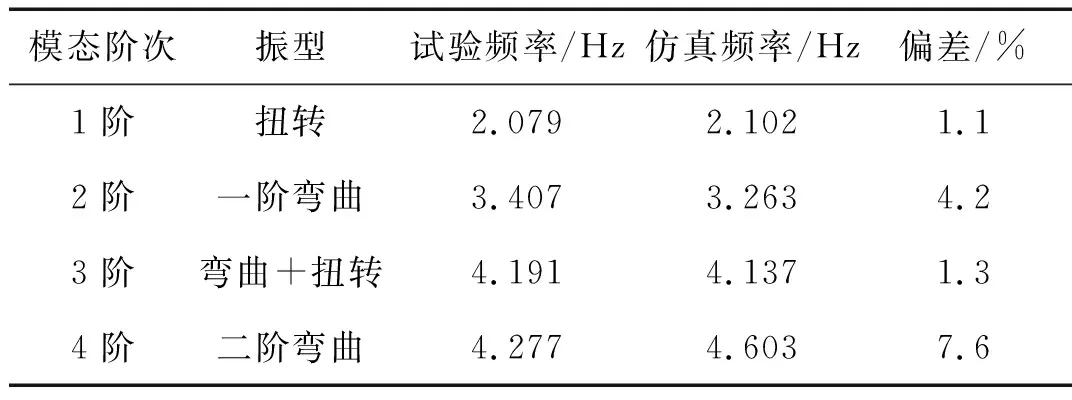
表8 五节含斜加劲索试验与仿真结果对比(二)Tab.8 Result comparison between the experiment and simulation of the five parts structure (2)

3.6 重力卸载装置的影响分析

增加悬吊装置后，会对结构模态产生影响[13]。试验选取气动-电磁悬挂装置作为重力卸载装置，其作用是尽可能地消除重力对大尺寸柔性结构的影响，模拟微重力环境。因此，作为对比，在仿真中去除吊绳，此时桁架结构具有6个空间自由度，基本等同于空间微重力环境。对此仿真结构进行模态计算，结果如表9。

从表9中看出，悬挂装置对结构的两种纯弯曲模态(水平面内弯曲)影响很小，对其他两阶模态影响很大，并增加了1阶模态。取无悬挂系统的3、4阶模态观察，如图8。这两种模态显示出结构在竖直方向上有较大变形，而悬挂系统会限制结构在竖直方向的变形，因此两种仿真结果关于竖直方向上有变形的模态差距较大；结构的两种纯弯曲模态都是在水平面内的变形，竖直方向上变形很小，因此两种仿真结果关于仅在水平方向上变形的模态差距较小。

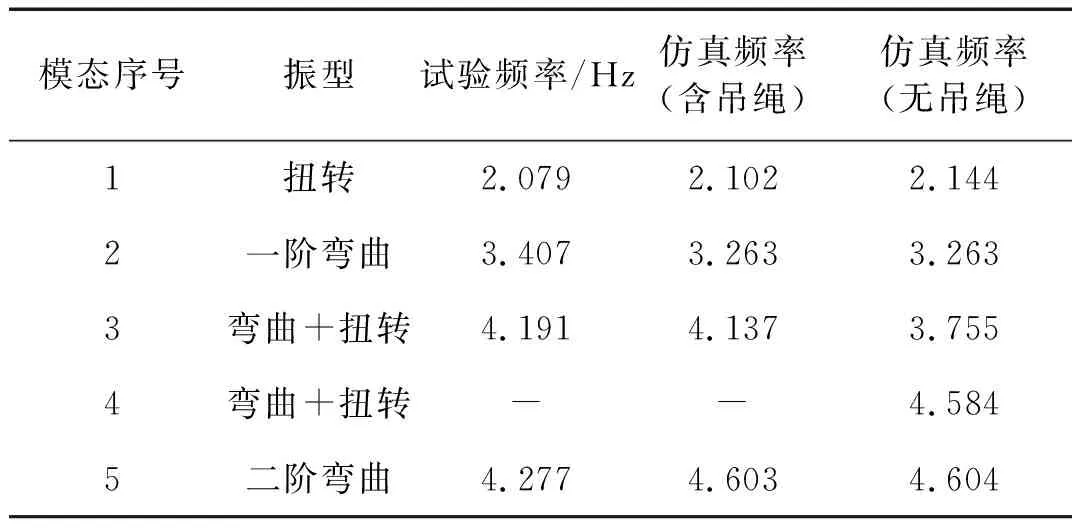
表9 重力卸载装置对模态试验的影响Tab.9 Influence of the gravity off-loading equipment to the modal experiment

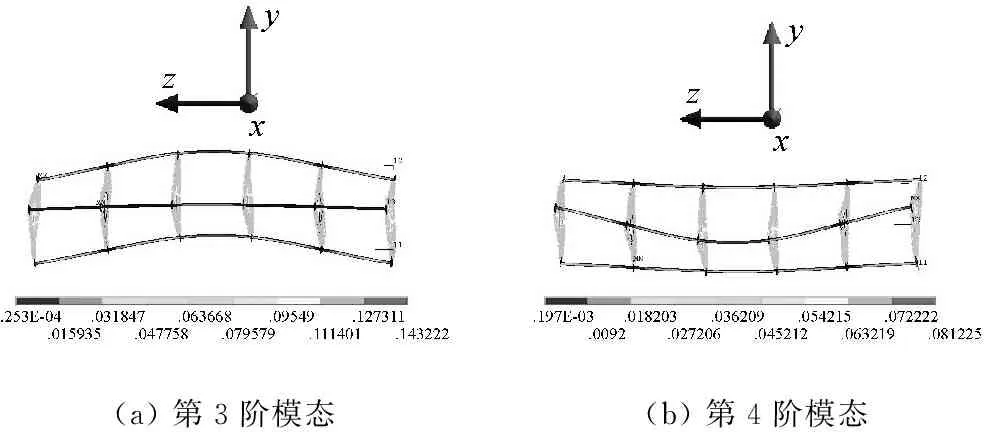
(a) 第3阶模态(b) 第4阶模态

图8 无悬挂系统仿真中的第3、4阶模态

Fig.8 The 3rdand 4thmodal of the simulation without suspension system

4 结 论

对一个由织物复合材料制成的空间可展桁架结构进行了微重力环境下的模态试验和仿真分析，仿真结果与试验结果基本一致。仿真中，将由织物复合材料制成的空心圆管简化为正交各向异性材料结构；将由铺层复合材料制成的三角形隔板简化为各向同性材料。

在单节桁架结构的研究中：仿真结果包含试验的前3阶模态，对应频率最大偏差5.7%，仿真模型基本合理；仿真中以隔板弯曲变形为主的模态在试验中未测出，原因是试验中未在隔板上布置传感器。在五节桁架结构的研究中，仿真结果与试验基本对应，对应频率最大偏差7.6%，仿真模型基本合理；仿真中结构扭转变形模态对应的频率与试验结果基本一致；仿真中，结构弯曲变形模态对应的频率与试验结果有差距，表明将织物复合材料简化为正交各向异性材料时，在计算结构弯曲变形模态对应的频率时，与实际值会有偏差。

斜加劲索的预应力不仅影响整体结构的刚度，同时会影响斜加劲索自身的弹性模量。当预应力达到一定值后，斜加劲索才会达到其固有弹性模量。本研究为斜加劲索预应力的设置提供参考依据。

进行了悬挂系统对结构模态仿真影响的研究，悬挂系统对在竖直方向上有变形的模态的影响较大，对仅在水平方向上有变形的模态的影响较小。